海底管道整體式止屈器性能研究與穿越壓力預測

徐萬海，龐 濤，閆術明，劉其民，李國輝

(1.天津大學 水利工程仿真與安全國家重點實驗室，天津 300072;2.中國石油天然氣管道工程有限公司，河北 廊坊 065000)

海底管道可用于高效率、低成本地輸運油氣資源，是海洋油氣開發中關鍵的裝備之一。深海海底管道長期處于高壓環境，當其局部存在缺陷或承受極端外壓時均會發生壓潰。局部壓潰會在慣性和外部水壓的聯合作用下傳遞至相鄰區域，使屈曲變形沿管長方向快速傳播。研究表明：管道屈曲傳播壓力Pp遠小于管道臨界壓潰壓力Pco，僅有壓潰壓力的18%左右，屈曲傳播的速率能達到每秒上百米，極易引發海底管道大范圍破壞，造成嚴重的經濟損失，極端時可誘發漏油等環境災難[1-5]。

實際工程中，通常在管道上增設止屈器來抑制管道屈曲傳播。通過間隔80～100 m安裝一個止屈器裝置[6]，增加管道的局部環向強度，使屈曲傳播限制在兩個止屈器之間，從而保證管道整體安全性[7]。目前，常見的止屈器類型可分為整體式、扣入式和纏繞式止屈器三種，在扣入式止屈器的基礎上還發展有焊接式和灌漿黏結式[8]。隨著海洋工程管道焊接技術的不斷發展，整體式止屈器以其強度高、止屈性能優良、適用水深范圍廣等優點得到了工程上的廣泛應用[9]。整體式止屈器是一種焊接布置在兩段管道之間的小段加強結構，其內徑與管道內徑相同，但壁厚更大，強度更高。如圖1所示，整體式止屈器的主要幾何參數包括：與管道相匹配的外徑D和壁厚t、止屈器整體長度Ls、止屈器有效長度La和厚度h等。

圖1 整體式止屈器Fig.1 Integral buckle arrestor

整體式止屈器的止屈性能和穿越壓力PX的大小成為人們關注的重點。Kyriakides[10]在管道壓潰和止屈問題研究中，率先提出采用如式(1)所示的止屈效率η衡量止屈器性能，該參數將管道壓潰壓力Pco和屈曲傳播壓力Pp與止屈器穿越壓力PX綜合考慮，可較好地反映止屈器的止屈效果。

(1)

Netto和Estefen[11]分別針對直徑和厚度之比(徑厚比)為16和23的兩種鋼管，開展整體式止屈器的穿越試驗研究，并擬合了相應的穿越壓力公式。Park等[12]和Lee等[13]分別開展整體式止屈器穿越試驗，并結合有限元模擬，將止屈器的穿越形式分為平行穿越和垂直穿越兩種，探究了止屈器參數對止屈性能的影響，并給出對應的穿越壓力公式。余建星等[14]開展了徑厚比為17和22.5的整體式止屈器模型試驗，并輔以有限元模擬，基于Netto和Estefen公式，進一步給出了整體式止屈器穿越壓力的表達式。DNV規范[15]在2007年的修訂中，增加了整體式止屈器穿越壓力的推薦公式。另一方面，隨著多年來的不斷發展，有限元技術已成功用于分析管道屈曲和止屈問題。Netto等[16]利用有限元模擬，分別計算了整體式止屈器在準靜態和動態條件下的穿越壓力，并與試驗結果進行對比，發現準靜態下穿越壓力相比動態條件更保守。Toscano等[17]指出有限元模型能對整體式止屈器的止屈性能進行較好預測。

表1為上述已發表的整體式止屈器穿越壓力計算公式。具體來看：DNV規范給出的公式結合了管道的屈曲傳播公式，將整體式止屈器的失效視為一種特殊的屈曲傳播現象，在止屈器的平行穿越階段具有較好的預測效果；Netto和Estefen、余建星等的公式具有類似的形式，可以反映相關參數對穿越壓力的部分影響，對于垂直穿越的預測卻有著較大的偏差；不同于上述3種公式，Lee的公式中額外引入了管道壓潰壓力Pco，以止屈效率η來衡量止屈效果，可一定程度上反映止屈器的止屈特性，但仍未明確給出整體式止屈器在不同穿越形式下穿越壓力的計算方法。后續的內容還將反映出這些公式在相同工況下的預測結果差別顯著，缺乏統一的計算標準。基于上述不足，利用有限元軟件ABAQUS對止屈器參數進行系統的敏感性分析，得到相應的穿越形式和穿越壓力，探究整體式止屈器的止屈特性，并在此基礎上，嘗試利用數值模擬結果擬合和優化，得到止屈器在不同穿越形式下穿越壓力的計算公式。

表1 海底管道整體式止屈器穿越壓力計算公式Tab.1 Calculation formulas for crossover pressure of integral buckle arrestor

1 有限元模型

通過ABAQUS軟件建立整體式止屈器的三維有限元模型，模擬海底管道的壓潰、屈曲傳播、止屈器止屈和失效全過程，從而探究整體式止屈器的穿越形式并獲取相應的臨界穿越壓力。模型主體包括管道缺陷段Lf、屈曲傳播段Lp、整體式止屈器段La、后屈曲段Lu、剛性面和腔體邊界，如圖2所示。建模過程中將管道與止屈器之間通過放樣的形式連接，并預留一定過渡段，同時基于結構幾何對稱性，建立1/4模型以提高計算效率。此外，為模擬屈曲發生后管道內壁間的接觸，在模型中預先設置了剛性面并忽略摩擦力。有限元模型的求解方法采用靜水流體單元(F3D4)法[18]，相較于弧長法更容易收斂且后屈曲過程計算更快。

圖2 有限元模型主體Fig.2 Finite element model

圖3展示了模型的網格劃分和單元類型選取，管道缺陷段和止屈段的網格均進行了細化處理，環向方向上均勻分布25～30份，厚度方向上劃分2～3份，可提高計算精度并減少計算成本。同時在管道和止屈器的連接處采用楔形網格過渡(C3D6)，實現網格整體規整。管道和止屈器的單元類型選擇八節點線性非協調單元(C3D8I)，避免了通用單元C3D8R在薄壁結構中的沙漏化問題。流體單元類型在.inp文件中設置為F3D4，通過指定靜水流體單元的輸入流量，實現腔體內部水壓加載。設置腔體內部水壓作為結果變量輸出，從而得到管道壓潰和止屈全過程的壓力變化。

圖3 模型網格劃分和單元類型Fig.3 Model meshing and element types

管道和止屈器的材料屬性采用Ramberg-Osgood本構模型描述，材料應力σ與應變ε滿足式(2)：

(2)

其中，E為材料彈性模量，n為材料硬化系數，σy為名義屈服應力。

有限元模擬管道壓潰及止屈的計算結果如圖4所示，分別展示了平行穿越和垂直穿越兩種模式，后續的分析會看到垂直穿越將會顯著影響止屈器的穿越壓力，使得該問題表現出一定的復雜性。圖5展示了模擬過程中艙體內部水壓的變化，艙體內部水壓經歷了兩個峰值，分別對應管道的臨界壓潰壓力Pco和止屈器結構的臨界穿越壓力PX，兩個峰值之間的平穩過渡段對應管道的屈曲傳播壓力Pp。

圖4 平行穿越和垂直穿越Fig.4 Parallel crossover and flipping crossover

圖5 腔體內部壓力變化曲線Fig.5 Curve of the pressure inside the cavity

有限元模擬還原了管道壓潰和止屈現象的全過程，艙內壓力曲線反映了管道及止屈器結構變形的臨界壓力大小。為驗證該有限元模型的正確性，文中基于上述模擬流程，計算得到了文獻[13]中3組整體式止屈器試驗工況下的穿越壓力，并與試驗結果進行對比，如表2所示。有限元模擬結果與試驗結果基本一致，誤差分布在6%以內，驗證了文中有限元模型的準確性。

表2 有限元模擬與試驗結果對比Tab.2 Comparison of finite element simulation and experimental results

2 參數分析

基于通過正確性驗證的有限元模型，改變模型中管道徑厚比D/t、整體式止屈器厚度比h/t、有效長度比La/t和材料屬性相關參數，文中系統地研究上述參數對止屈器結構強度和穿越形式的影響。表3匯總了相關參數的變化范圍，參數間相互組合形成上百組算例，基本涵蓋了工程中整體式止屈器常見的參數選取范圍。

表3 參數分析中各參數的變化范圍Tab.3 Variation range of each parameter in parameter analysis

2.1 管道徑厚比D/t

整體式止屈器在安裝時應與管道尺寸相匹配，管道徑厚比成為影響止屈器強度和止屈效果的重要因素之一。統計所有以管道徑厚比D/t(12.75～55)為自變量的計算結果，并對比DNV規范中整體式止屈器穿越壓力公式結果，如圖6所示。可以看出，在固定整體式止屈器的h/t=2、La/t=30的工況下，徑厚比D/t與穿越壓力呈反比關系，具體表現為管道徑厚比越小，止屈器穿越壓力的增長速率越快。

圖6 徑厚比D/t與穿越壓力曲線Fig.6 Curve of D/t and crossover pressure

對比DNV規范推薦公式的結果來看，不論是曲線的變化趨勢，還是特定點的數值對比，有限元模擬和DNV公式均表現出較好的吻合效果。特別是在徑厚比較大的薄壁管階段，二者計算所得的穿越壓力結果幾乎一致，這在一定程度上再次驗證了該有限元模型的準確性。

2.2 止屈器厚度比h/t

止屈器厚度是影響其自身結構強度的主要因素之一。固定管道的徑厚比為17、34和51，固定止屈器有效長度比La/t為15(對應D/t=17)和30(對應D/t=34、51)，改變有限元模型中止屈器厚度h與管道壁厚t的比值，實現對止屈器厚度的敏感性分析。圖7和圖8分別給出了D/t=17和D/t=34、51工況下止屈器厚度比與穿越壓力的變化曲線，同時還作出了0.2%初始橢圓度管道在外壓作用下的壓潰壓力Pco。

圖7 厚度比h/t與穿越壓力曲線(D/t=17)Fig.7 Curve of h/t and crossover pressure (D/t=17)

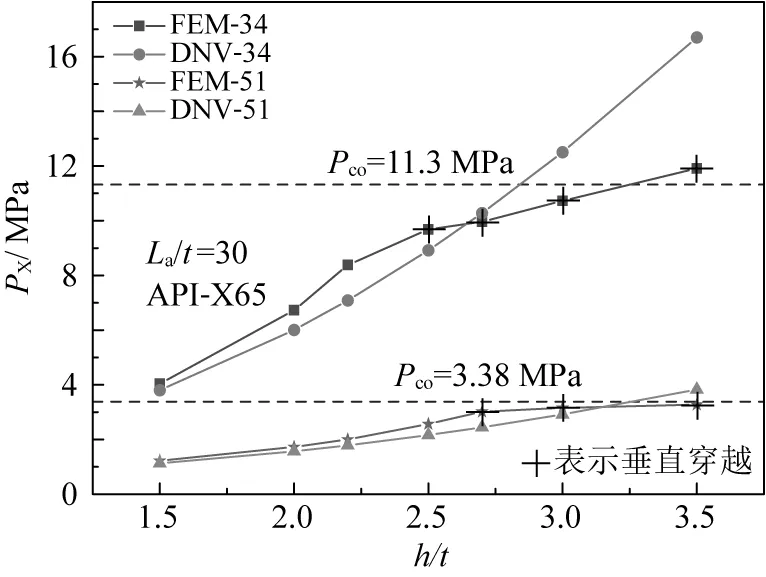
圖8 厚度比h/t與穿越壓力曲線(D/t=34、51)Fig.8 Curve of h/t and crossover pressure (D/t=34，51)

曲線的走勢表明，在固定止屈器長度和管道徑厚比時，隨著止屈器厚度h的增加，穿越壓力均呈現出一種先快速上升，隨后增長變緩(甚至停滯)的變化趨勢。同時注意到，增長速率發生變化時往往伴隨著垂直穿越的發生(曲線圖中“+”標記的數據點均為發生垂直穿越的算例，表現為下游管道屈曲的方向垂直于上游管道)，似乎是這種特殊的穿越形式削弱了整體式止屈器的止屈效果，使得繼續增大止屈器的厚度并不能達到預想的性能。Park等[12]指出垂直穿越通常發生在強度較高的整體式止屈器上，足夠強度的止屈器很難被壓扁，止屈器在吸收上游屈曲變形能量后傾向于發生一種類似剪刀結構的“十字”交叉變形(從能量的角度考慮，這是能量耗散最小的變形方式之一)，參見圖4。該理論可在一定程度上解釋垂直穿越對止屈性能的影響，但對于工程而言，平行穿越和垂直穿越的轉換區間即何時發生垂直穿越，同樣應當引起足夠重視。具體到上述算例，在不同徑厚比下，曲線中的拐點各不相同，同時下節針對止屈器有效長度比La/t的分析也表明了拐點的分布受多種因素影響，難以量化。引入管道臨界壓潰壓力Pco抵消徑厚比帶來的影響，關注止屈效率η隨厚度比h/t的變化，結果如圖9所示。可以看出垂直穿越均發生在止屈效率大于80%范圍內，考慮到止屈效率η(式(1))綜合了多個臨界壓力參數且垂直穿越對應較高的止屈效率，在后續的公式擬合中采用止屈效率η作為量化穿越形式轉換點的變量。

圖9 厚度比h/t與止屈效率曲線Fig.9 Curve of h/t and buckle arresting efficiency

此外，當止屈器的長度La較短時，以D/t=51工況為例(對應La/t=30)，該長度下止屈器不足以提供阻止屈曲傳播所需要的強度。需要額外增加止屈器長度或者繼續增加止屈器的厚度才可完全抑制屈曲傳播，但這樣增加了對鋪管設備性能的要求。因此為追求整體式止屈器的材料利用率而選用短且厚的結構形式是得不償失的，這樣的結構不利于管道鋪設，同時垂直穿越的存在使其止屈效果并不理想。

對比來看，DNV規范推薦公式并未考慮上述效應，h/t與穿越壓力總體接近線性正比關系。

2.3 止屈器有效長度比La/t

針對La/t的敏感度分析與h/t類似，同樣固定管道的徑厚比D/t和止屈器厚度h/t=2，改變La/t的值同時保證La/D在工程常用范圍0.5～1.5之內。相應的結果如圖10和圖11所示。

圖10 有效長度比La/t與穿越壓力曲線(D/t=17)Fig.10 Curve of La/t and crossover pressure (D/t=17)

圖11 有效長度比La/t與穿越壓力曲線(D/t=34、51)Fig.11 Curve of La/t and crossover pressure (D/t=34，51)

可以看出隨著La/t的增加，穿越壓力PX有著和h/t敏感性分析中相似的變化趨勢，在平行穿越階段，增加整體式止屈器的有效長度La可以有效增加止屈器的臨界穿越壓力PX，一旦進入垂直穿越(止屈效率在80%左右)，穿越壓力的提升便不再顯著。

對比來看，數值模擬結果在La/t較小時相比DNV公式高很多，La/t較大時則與DNV公式擬合較好。

2.4 止屈特性分析

整體式止屈器發生失效時具有兩種典型的穿越形式：平行穿越和垂直穿越。在平行穿越階段，增加整體式止屈器的厚度、有效長度和材料強度[13]能顯著增強止屈器自身的結構強度，從而增加穿越壓力的大小。但整體式止屈器的垂直穿越應當引起足夠重視，這種穿越形式往往對應較高的止屈效率(80%左右)，止屈器失效時本身并未發生較大形變。對于發生垂直穿越的止屈器，增加止屈器的相應參數并不能明顯提升其穿越壓力。

因此，徑厚比D/t、止屈器厚度h、有效長度La和材料屬性的合理配合才能使整體式止屈器的材料利用率達到最佳，在止屈器設計中要盡量讓上述參數落在最佳收益范圍之內。應當避免僅增加其中一個參數，因為垂直穿越的存在，在特定組合下，其中一個變量增大到一定程度后的收益便不再明顯了。此外，過短或過薄的止屈器也都是不可取的，這會極大地減弱其止屈性能并提高對鋪管設備的要求。

3 穿越壓力預測

3.1 公式擬合

考慮影響整體式止屈器穿越壓力的關鍵參數，包括管道徑厚比、止屈器厚度、長度比以及材料屬性，引入管道屈曲傳播壓力Pp，將整體式止屈器穿越壓力PX設定為以下無因次函數：

(3)

采用止屈效率η(式(1))衡量止屈器的止屈性能，考慮止屈效率η的形式，以及穿越壓力PX大于屈曲傳播壓力Pp，將函數簡化為以下冪函數的形式：

(4)

此時止屈效率η為：

(5)

取中間變量α為：

(6)

結合止屈器參數分析中非垂直穿越的有限元模擬結果，基于Levenberg-Marquardt最小二乘優化算法擬合式(4)中各個參數與目標函數的關系曲線，依次確定中間變量α中各冪指數的取值。隨后綜合所有有限元模擬結果，繪制于圖12中。

圖12 止屈效率η與中間變量α的關系擬合Fig.12 Fitting relationship between η and α

可以看出，中間變量α間接反映了管道徑厚比、止屈器厚度、有效長度和相應的材料屬性對穿越壓力的影響程度。當止屈效率0<η<0.7時(對應止屈器的平行穿越階段)，η與α的關系可近似為一條斜率A0=10.3的直線擬合；當止屈效率0.7≤η≤1時，由于垂直穿越的存在，止屈效率η和中間變量α的關系逐漸發散，呈現出一定的復雜性。此時采用一條線性包絡線作為止屈效率η的下界，對應的斜率A1=0.785 2、截距d=0.646 6，盡可能覆蓋所有樣本點，從而實現對全體模擬結果特別是對發生垂直穿越的算例的保守擬合。同時，對于垂直穿越的發生使得穿越壓力增長速率放緩這一特性，文中公式通過改變兩條增長曲線的斜率來體現。最終得到了式(7)的整體式止屈器穿越壓力計算公式：

(7)

需要說明的是，式(7)中止屈效率η的分布范圍并非對應止屈器穿越形式發生轉變的界限，而是對于該界限的保守擬合。從研究進行的算例結果可以看出該分界點分布在止屈效率η=80%左右，因此從工程安全的角度考慮，式(7)中兩種止屈效率范圍下的表達式(以止屈效率η=70%為界限)可分別用于計算止屈器的平行穿越和垂直穿越下的穿越壓力。同時，對于整體式止屈器何時發生垂直穿越，與哪些因素有關這一問題，后續可以開展進一步更為細致的研究。

3.2 試驗結果驗證

為了進一步驗證上述擬合公式的正確性和適用性，采用Park等[12]、Lee等[13]的試驗數據進行檢驗，模型參數和試驗結果如表4所示。將表4中試驗參數分別代入到余建星等公式[14]、DNV規范[15]、Lee等公式[13]和文中擬合得到的公式中，計算整體式止屈器的穿越壓力大小，如表5所示。

表4 Lee等[13]、Park等[12]模型參數和試驗結果Tab.4 Model parameters and experimental results of Lee,et al[13] and Park，et al[12]

表5 穿越壓力PX計算值與試驗值對比Tab.5 Comparing the calculated values of crossover pressure PX with the experimental values

同時將表中數據作可視化處理，繪制于圖13中。結合圖表中的數據可以看出：文中擬合的穿越壓力計算公式與試驗結果吻合程度較好，平均誤差僅為-3.5%；相比之下，余建星等公式[14]和DNV規范[15]計算結果明顯大于試驗值，個別試驗工況的偏差甚至達到了56.0%和75.8%；Lee等公式[13]表現為明顯偏保守，在與試驗結果的對比中，其整體誤差和誤差極值分別達到了-7.0%和-18.6%。

圖13 公式計算值與試驗值的標定Fig.13 Calibration of formula values and experiments

文中提出的公式相較于已有的規范或學者擬合公式不論是在適用范圍，還是結果準確性上都有著顯著的優勢，能夠較為準確地預測出整體式止屈器穿越壓力PX這一重要設計參數，從而指導設計。

4 結 語

利用ABAQUS有限元軟件，對管道整體式止屈器的止屈和穿越過程進行了模擬，分析了止屈器的止屈特性，基于大量有限元模擬結果對整體式止屈器穿越壓力進行了公式擬合，得到以下結論和成果：

1) 平行穿越階段，增大管道徑厚比D/t、止屈器厚度h、有效長度La可以有效提升止屈效率，但進入垂直穿越階段后，這種提升效果便不再顯著。管道徑厚比D/t、止屈器厚度h、有效長度La的合理配合才能使整體式止屈器的材料利用率達到最佳，過短或過薄的止屈器都是不可取的，同時應避免一味增加止屈器的一個參數。

2) 提出了一種預測整體式止屈器穿越壓力的快速計算公式。將文中公式、Lee等公式、余建星等公式、DNV規范的計算結果與已發表的整體式止屈器試驗結果進行對比分析，文中公式具有更高的準確性。同時針對不同的穿越形式給出了不同的計算式，可為工程實際中整體式止屈器的設計提供指導和參考價值。

盡管研究針對整體式止屈器的不同穿越形式給出了不同的穿越壓力計算公式，但對于兩種穿越形式的轉變區間僅進行了保守選取(文中以止屈效率η=70%為界限)，并未進行深入細致的探究。在整體式止屈器何時發生垂直穿越，具體與哪些因素有關這一問題上，有待后續開展更為嚴謹準確的研究。同時，整體式止屈器的最優參數區間、最佳材料利用率也是一個值得進一步研究的問題。