變工況運行中結構參數對螺旋槽動壓推力氣體軸承承載力的影響

李云龍，董志強

(太原科技大學 機械工程學院，太原 030024)

螺旋槽動壓推力氣體軸承的表面刻有微米級的溝槽，按溝槽形式分為泵入型、泵出型和人字槽型，因其具有較高的承載力和較好的穩定性，在高速旋轉機械和儀器中，特別是在航空航天儀器中得到了較廣泛的應用，如慣性導航陀螺儀、低溫透平膨脹機等[1-3]。螺旋槽動壓氣體軸承理論計算的發展初期是由納維-斯托克斯(N-S)方程推導而成，經一系列的簡化成為壓縮性流體的非定常雷諾方程，從而求出近似解。文獻[4]用 Whippler的窄槽理論研究了等間距排列的平行槽與平行板之間的流動，結果表明該理論適用于低轉速的軸承；文獻[5]提出的準不可壓縮窄槽理論可應用于各種形狀軸承的研究，但假定仍有不合理的地方使計算值誤差較大；文獻[6]提出了變函數保角變換理論方法，重點考慮了槽端部的影響；文獻[7]采用差分法在變換坐標系后進行了潤滑方程的計算；文獻[8]采用有限元法對控制方程進行求解，得到了槽端半徑比、螺旋角、氣膜厚度比、槽數等對氣膜承載力的影響；文獻[9]用伽遼金方法對控制方程進行了變換，采用有限元法計算得到了壓力分布；文獻[10]采用有限體積法得到了氣體軸承的離散方程，研究了軸承結構參數對承載力和摩擦力矩的影響，證明了有限體積法的可行性。

關于采用不同結構來改進軸承性能，國內外外學者做了大量的研究，分析了矩形槽、T形槽等螺旋槽槽形對軸承性能的影響。但大多通過求解雷諾方程分析空氣軸承的性能而并未直接從N-S方程入手，不斷嘗試改進螺旋槽型、結構尺寸等參數都是為了改進軸承性能，增大軸承承載力，但較為全面地對軸承氣膜承載力進行專門研究的探索較少。

為進一步從N-S方程了解多方面參數對軸承氣膜承載力的影響，本文采用有限體積法并應用ANSYS—CFD(計算流體力學)軟件對泵入型螺旋槽動壓推力氣體軸承進行數值模擬，分析特定工況下的端面流動狀態，并在多種轉速下對比分析不同槽數、螺旋角、槽深、臺區軸承間隙、槽內徑比、槽寬比和不同槽底結構以及泵入型、泵出型軸承結構對軸承氣膜承載力的影響。

1 理論模型與計算方程

1.1 結構與理論

螺旋槽動壓推力氣體軸承結構如圖1所示，軸承分為槽區、臺區及密封區，軸承外圈半徑為re，內圈半徑為ri，螺旋線的基圓半徑為rg，設臺區軸承間隙為h1，螺旋槽深h2，則氣膜總間隙h=h1+

圖1 螺旋槽動壓推力氣體軸承的結構

h2，軸承外周圓上臺區脊寬為b1,螺旋槽寬為b2，槽寬比γ=b1/b2，槽內徑比λ=(re-rg)/(re-ri)。通常情況下螺旋線采用對數螺旋線形式，其極坐標為

r=rgeθtan α，

(1)

式中：r為螺旋槽的極半徑；θ為角度坐標；α為螺旋角。

選取的軸承模型有12對槽臺，由于軸承端面幾何模型符合周期性分布和中心分布原則，所以氣膜層分布同樣符合周期性原則，為節省計算時間，提高計算效率，選取計算區域的1/12(端面1個槽臺區和相連的密封壩區)建模，如圖2所示。由于氣膜厚度是微米級，氣膜總間隙一般為幾十微米左右[11]，將氣膜導入ICEM網格劃分軟件中進行網格劃分難度非常大，所以對氣膜在厚度上放大100倍，以便于觀察及網格劃分，進行流體模擬仿真時，在FLUENT軟件中恢復原尺寸。

圖2 螺旋槽動壓推力氣體軸承的三維模型

強制性邊界條件為

(2)

式中：p為氣體壓力；pin進口壓力；pout為出口壓力。

周期性邊界條件為

p(r,θ)=p(r,θ+2π/Ng)，

(3)

式中：Ng為螺旋槽數。

1.2 理論假設

基于N-S方程的質量守恒定律、動量守恒定律、能量守恒定律并考慮螺旋槽動壓推力氣體軸承自身結構特性，做如下假設：

1)忽略氣體的體積力和慣性力；

2)氣體分子在界面牢固吸附，無滑移；

3)忽略重力產生的影響；

4)氣膜流場分析采用穩態定常；

5)忽略壁面粗糙度的影響；

6)軸承與推力板嚴格對中，忽略工作中系統擾動、偏擺對氣膜流場的影響。

1.3 計算方程

1.3.1 N-S方程

在黏性氣流中取出一微元體，分別對6個面進行受力分析，如圖3所示，圖中σ為微元體作用面的壓應力，τ為微元體作用面的切應力。

圖3 黏性氣流微元體

規定x方向為運動方向，則黏性氣流微元體在x軸方向的受力由牛頓第二定律計算，即

(4)

(5)

(6)

(7)

fxρdxdydz+

(8)

化簡得

(9)

切應力由廣義牛頓內摩擦定律確定，即

(10)

壓應力為

(11)

式中：v為速度；t為時間;ρ為密度；μ為分子動力黏性系數；f為質量力。

div(υ)為速度的散度,令

(12)

(9)式化簡為

(13)

同理可得y，z方向的方程式為

(14)

(15)

1.3.2 層流方程

層流控制方程采用可壓縮完全氣體雷諾方程，在極坐標下為[12]

(16)

式中：n為軸承轉速。

1.3.3 其他方程

軸承承載力方程為

(17)

式中：p(r,θ)為氣膜壓力分布函數。

摩擦阻力方程為

(19)

氣膜剛度方程為

(20)

2 計算流程

軸承氣膜承載力計算流程如圖4所示，選取螺旋槽動壓推力氣體軸承設計參數見表1。

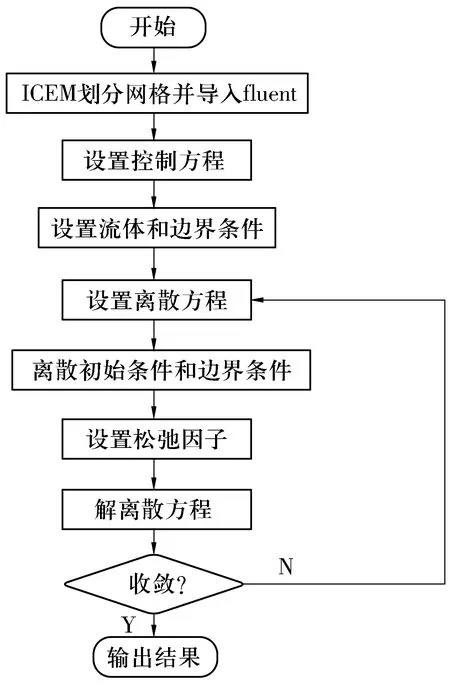
圖4 軸承氣膜承載力的計算流程

表1 螺旋槽動壓推力氣體軸承參數

利用ICEM軟件對計算區域模型的1/12劃分網格，采用6面體結構網格，利用mesh功能對周期壁面設置為旋轉周期性的邊界條件(圖2)，采用extrude face功能劃分的網格如圖5所示，為驗證數值分析的可靠性，需要進行網格無關性檢驗，不同節點數的承載力見表2，劃分方法1與劃分方法2誤差約為6%，劃分方法2與劃分方法3所得承載力誤差約為1.5%，當不同節點數誤差小于2%時即可用，綜合考慮計算機配置情況等本文選用最終生成節點數為81 270，壩區、臺區網格為5層，槽區網格為15層。

圖5 ICEM網格劃分

表2 不同節點數的承載力

3 結果與討論

采用Pressure-Based求解器，時間設置為穩態，出入口壓力均為101 325 Pa，周期邊界periodic-1，periodic-2設置為旋轉邊界，轉速n=40 000 r/min，基于N-S方程，本文采用應用較廣的SIMPLE算法，為提高精度，方程對流項離散采用二階迎風格式[13]。

3.1 流態分析

雷諾數判定法的計算公式為[14]

(21)

式中：U為流體流速；L為流體黏性系數。

將U等同為平均旋轉線速度v，L等同為氣膜總間隙h，re=25.0 mm，ri=12.5 mm，空氣密度ρ=1.29 kg/m3，黏度μ=1.789×10-5Pa·s，氣膜總間隙h=40 μm，轉速n=40 000 r/min,由

(22)

解得Re=2.27。

由雷諾數判定準則知，當Re≤2 300時為層流，2 3004 000時為完全湍流狀態，因此可判定流動狀態為層流。

3.2 氣體壓縮密度分析

氣體壓縮密度及徑向密度分布如圖6所示，徑向線段為從圓心沿直徑方向的一條線段，氣流狀態為層流。軸承高速旋轉時，由于泵入效應，氣體不斷由入口送入螺旋槽內，在螺旋槽根部受到壩臺的阻擋，瞬間氣體被壓縮，密度和壓力增大，起到承載作用;在17.7 mm處即槽根部壓縮后，密度達到最大(2.847×10-3kg/m3)，之后不斷下降，出口處最小。

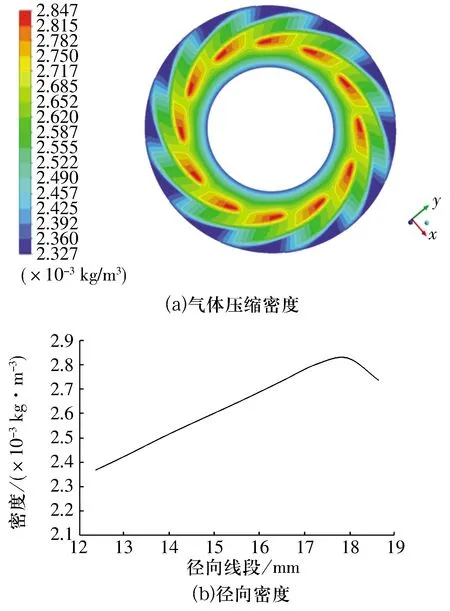
圖6 氣體壓縮密度分布及徑向密度分布

3.3 不同結構參數對軸承氣膜承載力的影響

3.3.1 槽深

不同槽深的氣膜承載力如圖7所示：不同轉速下氣膜承載力變化趨勢相同，泵入型螺旋槽動壓推力氣體軸承氣膜承載力由泵氣效應和周向階梯效應決定，槽深可直接影響氣膜承載力，隨著槽深的不斷增大，軸承的泵入效應不斷增強，當槽深為40 μm時泵氣效應達到最大，此時氣膜承載力最大,說明槽深變化對氣膜承載力的影響較大，槽深可取30～50 μm。

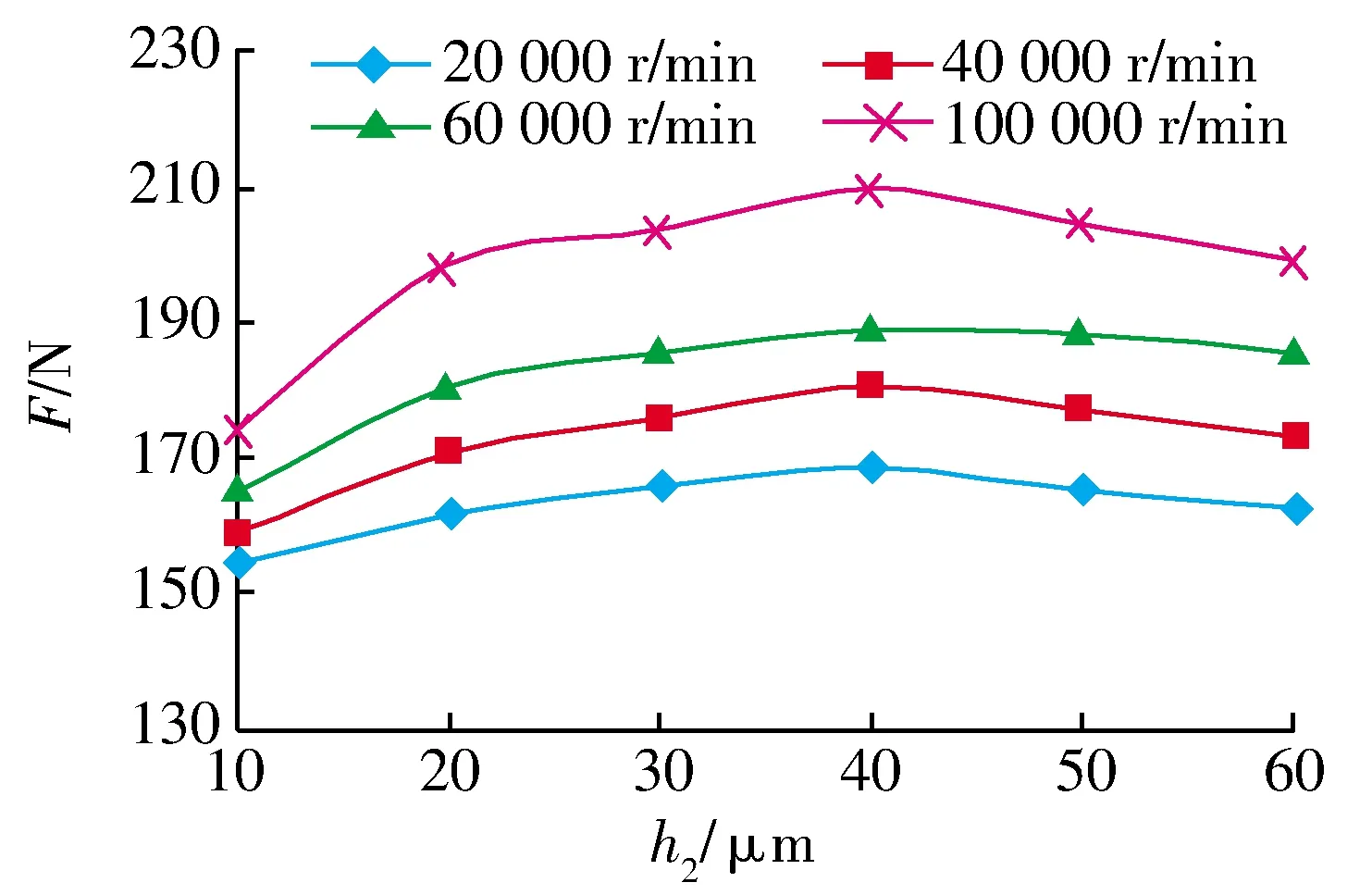
圖7 不同槽深的氣膜承載力

3.3.2 螺旋角

螺旋角是影響軸承泵氣效應的重要參數，不同螺旋角的氣膜承載力如圖8所示：不同轉速下氣膜承載力的變化趨勢相同，隨著螺旋角的增大，軸承的泵氣效應增大，氣膜承載力增大，螺旋角增大到一定數值后開始下降，在27°時泵氣效應達到最大，氣膜承載力最大，因此螺旋角可取18°～36°。

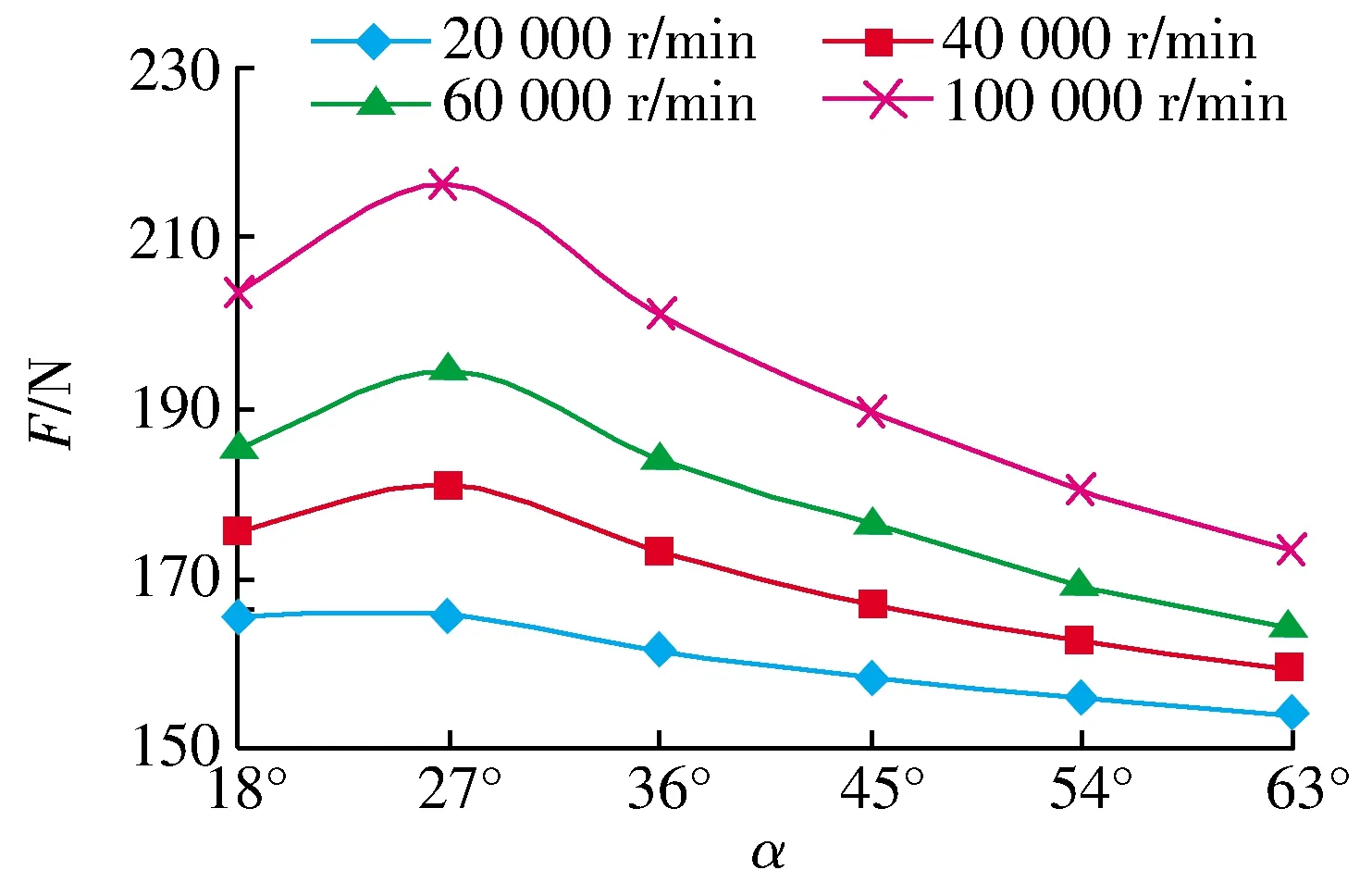
圖8 不同螺旋角的氣膜承載力

3.3.3 臺區軸承間隙

不同臺區軸承間隙的氣膜承載力如圖9所示:不同轉速下氣膜承載力變化趨勢相同，隨臺區軸承間隙增大，氣膜承載力不斷下降。實際工作中需要較大氣膜承載力時可以通過調整臺區軸承間隙來實現，不過臺區軸承間隙過大時氣膜承載力過小，臺區軸承間隙過小時軸承與轉子之間會有摩擦，因此臺區軸承間隙可取4～10 μm。

圖9 不同臺區軸承間隙的氣膜承載力

3.3.4 槽內徑比

不同槽內徑比的氣膜承載力如圖10所示:不同轉速下氣膜承載力的變化趨勢相同，隨著λ的增大，氣膜承載力不斷增大，當λ為0.6～0.8時，氣膜承載力達到最大。結合文獻[15]中的λ在0.7附近有一最佳值，可知計算結果的準確性。

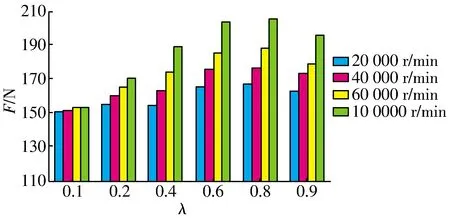
圖10 不同槽內徑比的氣膜承載力

3.3.5 槽寬比

理論上軸承在無槽和全槽時都不會有階梯效應，因此槽寬比對氣膜承載力有一定的影響。不同槽寬比的氣膜承載力如圖11所示:不同轉速下氣膜承載力變化的趨勢相同，在槽寬比約為0.8時有較大的氣膜承載力，槽寬比可取0.7～0.9。

圖11 不同槽寬比的氣膜承載力

3.3.6 槽數

不同槽數的氣膜承載力如圖12所示：單從槽數來說，槽數越多，氣膜承載力越大；當槽數由5增加到10時，氣膜承載力快速增加,之后隨著槽數的不斷增加，氣膜承載力的增加逐漸趨于緩慢，槽數的增加使加工難度增加，所以不能完全只通過增加槽數來提高氣膜承載力，槽數可取Ng=12～25。

圖12 不同槽數的氣膜承載力

3.3.7 槽底結構

平底、凸型、凹型槽的氣膜承載力如圖13所示，凸、凹型槽是在原有的2 μm的槽深上，在與端面接觸的1 μm的槽深中設置為凸面和凹面，凸面和凹面圓周角度為10°。由圖13可知，凸型槽的氣膜承載力最大，其次為平底槽，最后為凹型槽，并且轉速的增大使氣膜承載力的差距明顯。

3.3.8 螺旋槽結構

部分溝槽可分為泵入型、泵出型，如圖14所示。

圖13 不同槽底結構的氣膜承載力

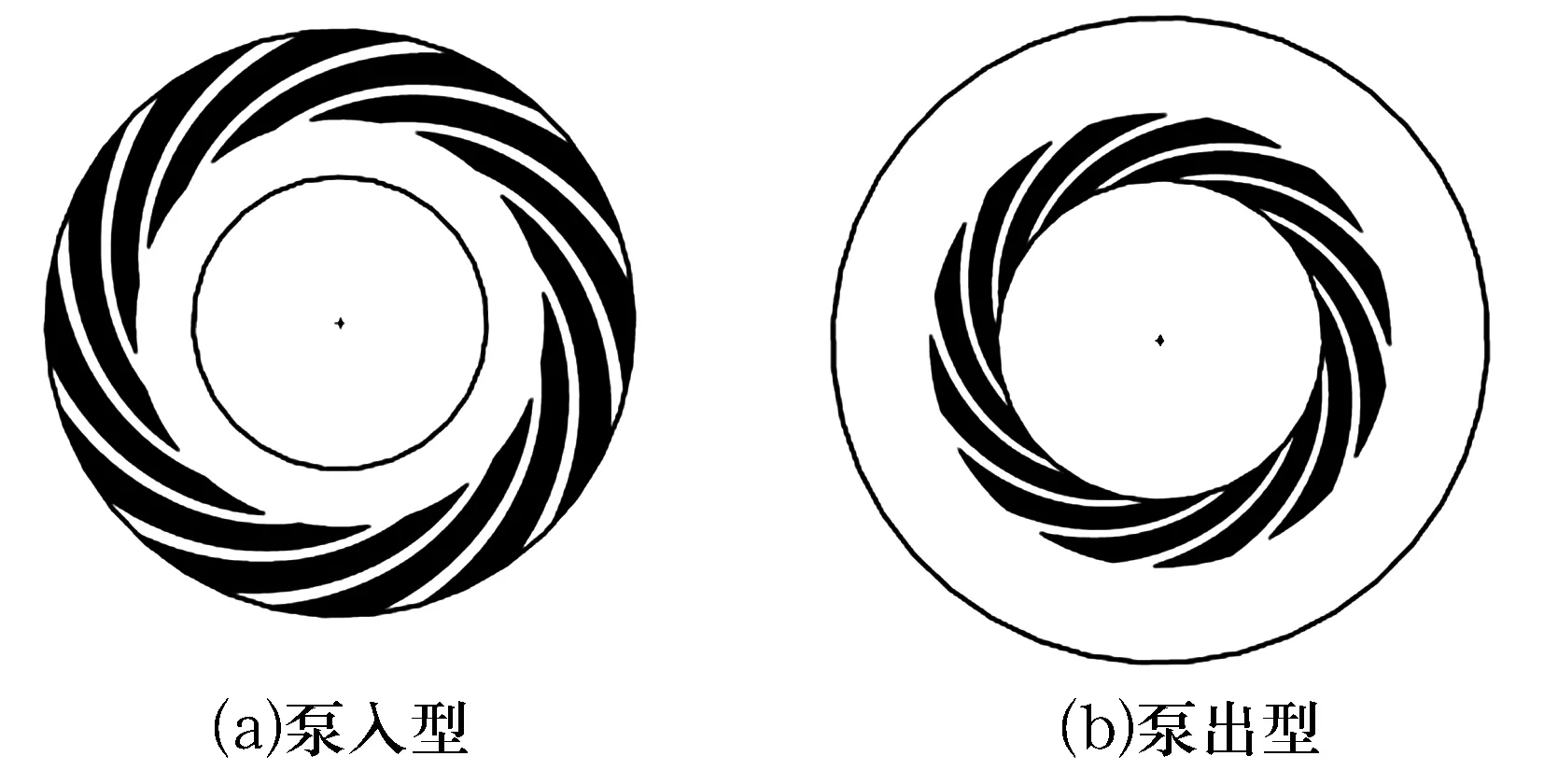
圖14 泵入型、泵出型螺旋槽動壓推力氣體軸承

不同轉速下泵入型、泵出型推力氣體軸承的氣膜承載力如圖15所示:泵入型比泵出型的氣膜承載力要高[16]，并且隨著轉速的增大，泵入型氣膜承載力增加明顯，泵出型氣膜承載力增加緩慢，轉速從20 000 r/min到120 000 r/min,泵入型氣膜承載力從165.72 N增加到212.28 N,泵出型氣膜承載力從157.80 N增加到179.16 N，二者最大承載力相差33.12 N,因此在實際運行中可結合工況運行優先選用泵入型軸承。

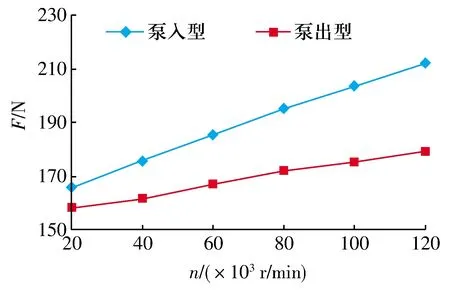
圖15 不同工況下泵入型、泵出型推力氣體軸承的承載力

4 結論

基于N-S方程，采用有限體積法并結合CFD軟件對螺旋槽動壓推力氣體軸承進行數值模擬，得到以下結論：

1)通過雷諾數判定氣膜流動為層流，利用氣體的可壓縮性，可得到軸承高速旋轉中氣體的壓縮密度分析圖，結果顯示在槽根處氣體密度最大，進而可進行氣膜承載力的分析。

2)對比分析不同參數對軸承氣膜承載力的影響，根據分析結果給出了槽型幾何參數的取值范圍：槽深為30～50 μm，螺旋角為18°～36°，臺區軸承間隙為4～10 μm，槽內徑比為0.6～0.8，槽寬比為0.7～0.9，槽數為12～25，凸型槽>平底槽>凹型槽，泵入型氣膜承載力大于泵出型，可優先選用泵入型軸承。