煤礦水平孔復雜地質模型方位電磁波響應數值模擬

張 意，康正明，馮 宏，韓 雪，陳 剛

(1.煤炭科學研究總院，北京 100013；2.中煤科工集團西安研究院有限公司，陜西 西安 710077；3.西安石油大學 電子工程學院，陜西 西安 710065；4.中國石油集團測井有限公司，陜西 西安 710077)

我國煤炭開采已逐步普及自動化并進入智能化發展階段[1]，煤巖界面識別是實現煤礦巷道自動化掘進和煤礦智能化的關鍵技術之一[2-4]。現有測井巖性界面識別技術中，方位電磁波測井因探測范圍較大(根據所使用源距和頻率的不同，商用儀器的探測深度及探邊距離可達幾米至幾十米)，能夠分辨煤巖界面方位，可探測低阻異常體等優勢，其理論發展和技術進步對煤礦智能化發展具有重要意義[5-7]。

傳統電磁波測井儀采用軸向發射和軸向接收線圈，能夠適用于隨鉆測量環境，但只能測量地層電阻率，無法測量巖性界面信息[8-10]。隨著水平井鉆井技術的發展，隨鉆地質導向需要一種能夠識別地層界面的方法，從而使方位電磁波測井儀器得到發展，其采用軸向線圈和傾斜/水平線圈相結合的組合方式，能夠同時測量電導率和巖性界面信息[11-14]。現有商業方位電磁波測井儀器針對油田測量環境設計，而油田測量環境和煤田測量環境具有較大不同：①油田測井目標地層的電阻率較低(小于100 Ω·m)，而煤層的電阻率值范圍較大(20～10 000 Ω·m)，已發表論文中對高阻情況的討論較少；② 相對于油田測井，煤田常用的鉆桿尺寸較小，電阻率各向異性處在高電阻率范圍，煤田測量情況下儀器、地層參數變化對方位電磁波探測特性的影響尚不明確；③煤田測量儀器存在本質安全要求，儀器設計和制造需要滿足煤礦測量的安全要求；④ 相對于油田測井，煤田測井對電阻率值的準確測量要求不高，但對煤巖界面位置的測量精度要求較高。

已發表的論文中針對煤田測井的方位電磁波測井研究較少，主要研究有：順煤層鉆進隨鉆方位電磁波頂底板探測影響因素[15]；電導率、介電常數與發射頻率的關系，以及煤矸石、源距、頻率等對方位電磁波測量響應的影響[16-17]；水平孔煤巖界面方位電磁波測井儀器探測性能[18]。上述研究主要采用的是水平層狀地層模型，復雜3D 地質模型中的鉆孔、采空區、起伏地層響應尚不明確，本文針對3～6 m 厚的煤層，采用3D 有限元數值模擬方法，建立鉆孔、采空區、起伏地層3 種典型地質模型，研究不同源距和發射頻率情況下的鉆孔、采空區、地層起伏等環境參數變化對方位電磁波測量響應的影響。

1 儀器參數及基本原理

1.1 正演模擬儀器參數

目前沒有針對煤礦測量環境的商用方位電磁波測井儀器，為分析方位電磁波測井在煤礦復雜3D 地質模型中的響應特征，使用較成熟的油田方位電磁波測井PeriScope 儀器參數進行有限元正演模擬，以分析其對復雜3D 地質模型的探測效果。PeriScope 儀器線圈系中，傾斜線圈既能探測徑向分量又能探測軸向分量，本文主要研究傾斜線圈對煤巖邊界的探測能力。如圖1 所示，PeriScope 儀器傾斜線圈系采用4 種工作源距L：0.558 8、0.863 6、2.133 6、2.438 4 m，用于探測巖性邊界的地質信號采用3 種發射頻率：0.1、0.4、2.0 MHz(下文也稱其為低頻、中頻、高頻)。

圖1 PeriScope 方位電磁波測井儀結構Fig.1 Structure of PeriScope azimuth electsromagnetic wave logging tool

1.2 基本原理

當采用時諧源exp(?jωt)時，電磁波測井電磁場滿足微分Maxwell 方程組[19-20]：

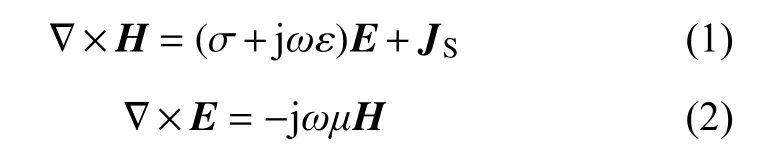
式中：H為磁場強度矢量，A/m；E為電場強度矢量，V/m；JS為外加電流密度矢量，A/m2；ω為角頻率，rad/s；σ為電導率，S/m；ε為介電常數，F/m；μ為磁導率，H/m；j 為虛數單位。

將式(2)兩端求旋度并代入式(1)中可得：

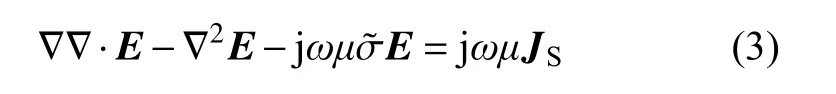
利用變分原理和泛函分析，可得電場強度矢量E的泛函表達式[21]：

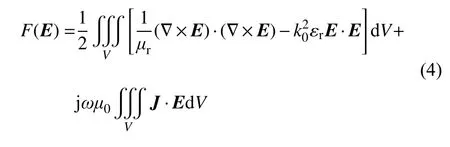
式中：F(E)為電場強度矢量E的泛函；μr為相對磁導率；μ0為真空中磁導率，μ0=4π×10?7H/m；；εr為相對介電常數；k0為自由空間波數，rad/m；V為體單元。

將求解域離散成若干個子空間，在子空間坐標系下，對每個單元利用形狀函數導出場量求解表達式，并擴展到總矩陣方程：

式中：A為總剛度矩陣；X為未知量；b為施加條件。通過求解式(5)可得到整個求解域電磁場分布。

對電場強度進行線積分可得到不同方位的電壓信號。傾斜線圈地質信號計算常用的一種方法是，測量傾斜線圈在儀器沿軸線旋轉到不同方位角α1和α2(α1和α2常取0°和180°)時的接收電動勢，將其轉化為幅度比和相位差地質信號：

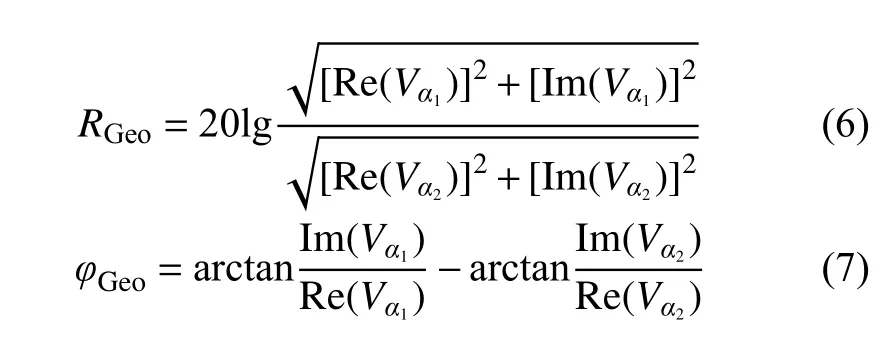
式中：RGeo為幅度比地質信號，dB；φGeo為相位差地質信號，(°)；Vα1為接收在角度1 時的測量電壓，V；Vα2為接收在角度2 時的測量電壓，V。Re表示取電壓的實部信號，V；Im表示取電壓的虛部信號，V。

2 鉆孔的影響

煤礦鉆井不僅使用泥漿鉆進的方式，也使用風鉆等鉆進方式，工作面探放水孔或瓦斯抽采孔在完鉆后通常保持裸眼狀態，孔中介質除泥漿外還存在空氣或地層水的情況。鉆孔半徑、孔中介質與孔壁地層的巖性分界面都對測量響應有一定影響，為研究方位電磁波測井響應受煤礦鉆孔的影響，建立如圖2 所示的三層水平分層地層模型，其中X軸為水平方向(X軸位于煤層中心)，Z軸為豎直方向，Y軸垂直紙面向里，H為煤層厚度，ρC為煤層電阻率，ρU為頂板電阻率，ρD為底板電阻率，rT為儀器半徑，rB為鉆孔半徑，d為偏心距，ρm為鉆孔中介質電阻率。另外，f為發射頻率。

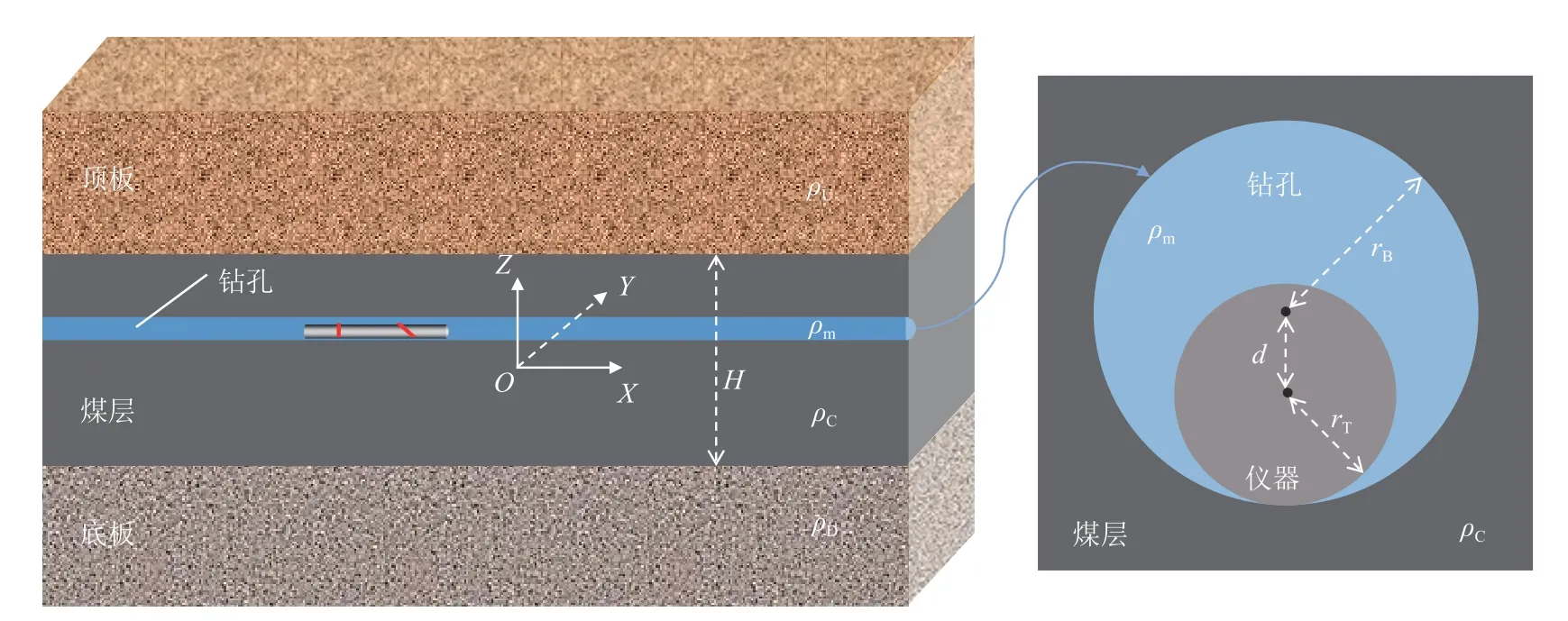
圖2 鉆孔地質模型及鉆孔橫截面示意Fig.2 Borehole geological model and borehole cross section

2.1 鉆孔介質

在儀器居中時，為計算煤田常用鉆桿直徑和孔徑參數下方位電磁波測井測量響應特征，在如圖2 所示的模型中設置模型參數：H=5 m，ρC=200 Ω·m，ρU=10 Ω·m，ρD=10 Ω·m，rT=3.65 cm(直徑73 mm 的鉆桿在煤礦井下鉆井作業中較為常用)，rB=5 cm，d=0 m(儀器居中)，ρm=0.1(鹽水)、10(淡水)、107(空氣) Ω·m，f=0.4 MHz。儀器保持水平且儀器中心處于相同的X位置，鉆孔在不同深度位置的方位電磁波測量結果如圖3 所示(相當于在不同Z深度位置分別打水平孔，每個鉆孔只測量一個相同X位置的點)，可以看出當儀器居中時，相同源距下，模型中不含鉆孔、模型含充水鉆孔、模型含充空氣鉆孔的方位電磁波測量曲線差異可以忽略不計，也即儀器居中時鉆孔流體對方位電磁波的影響較小，在實際測量時應盡可能讓儀器保持居中狀態，也即儀器居中測量時無需進行井眼影響校正。

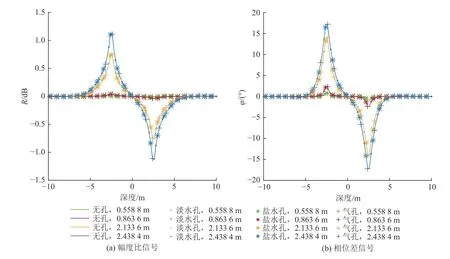
圖3 鉆孔介質影響對比Fig.3 Comparison of the influence of media in drilling hole

2.2 偏心距

為計算不同偏心距對方位電磁波測量響應的影響，在含鉆孔的均質模型中設置模型參數：H=100 m，ρC=200 Ω·m，ρU=200 Ω·m，ρD=200 Ω·m，rT=3.65 cm，rB=7.5 cm，d=0～3.85 cm，ρm=0.1、10.0 Ω·m，f=0.1、0.4、2.0 MHz。不同發射頻率時的方位電磁波測量響應如圖4 所示，可以看出，當鉆孔中為淡水時，模型設置的偏心距對幅度比和相位差影響較小，可以忽略不計。當鉆孔中為鹽水時，幅度比信號受偏心距的影響較小，相位差受偏心距的影響較大；隨偏心距增加，鉆孔水對方位電磁波地質信號的影響增大，且隨頻率的增加，其對地質信號的影響也增大；對于地質信號的常用閾值(幅度比信號0.25 dB，相位差信號1.5°)，在鉆孔半徑為7.5 cm，鉆孔偏心距大于1 cm 時，0.558 8 m 和0.863 6 m 源距在2 MHz 頻率時的相位差信號需要做偏心影響校正或在測量時為儀器添加扶正器，其他源距和發射頻率下，偏心距的影響較小。

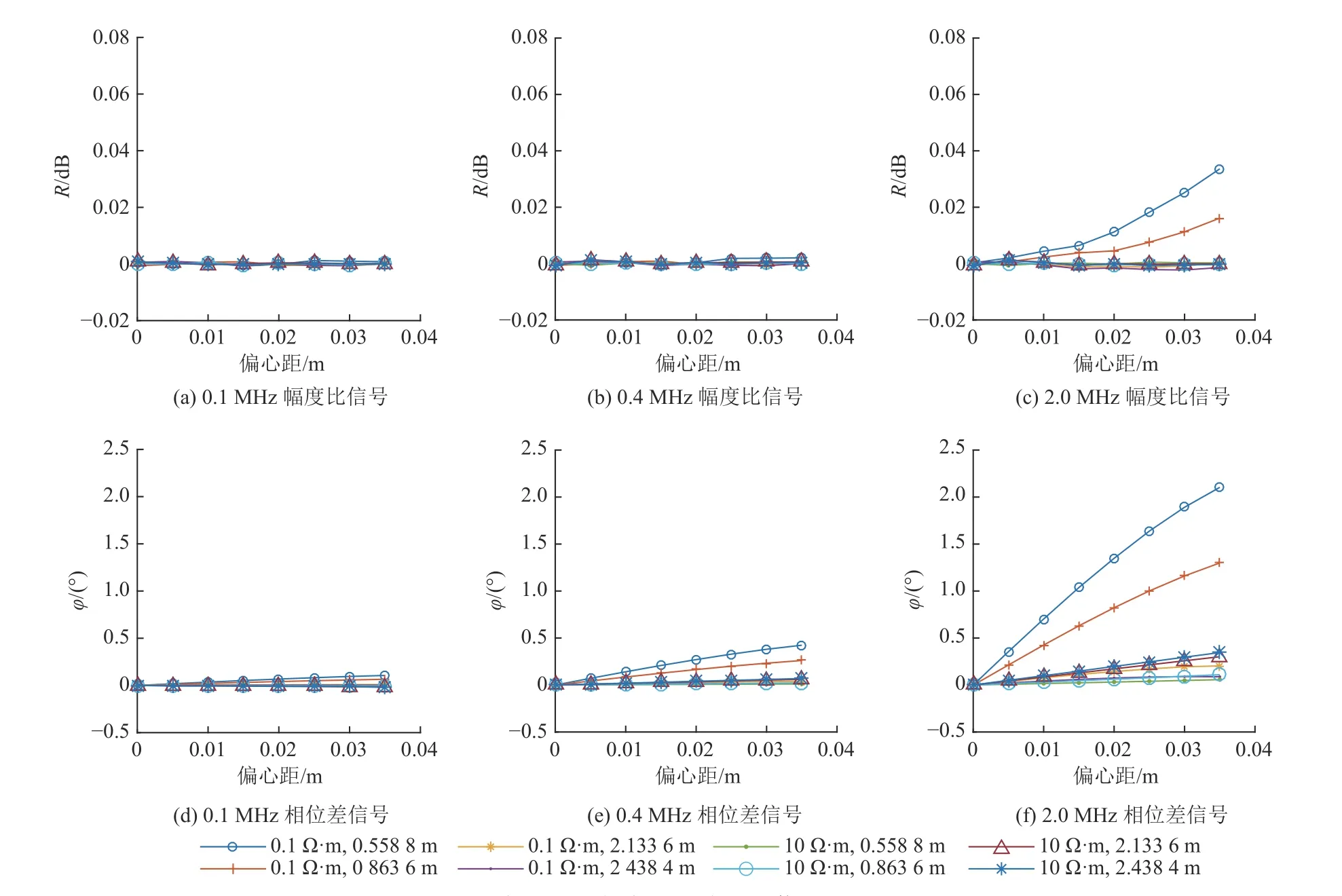
圖4 偏心距對方位電磁波測量信號的影響Fig.4 Influence of eccentricity on electromagnetic wave measurement signal

2.3 鉆孔半徑

在含鉆孔的均質模型中，為計算儀器始終位于鉆孔底部時鉆孔流體對測量響應的影響，設置模型參數：H=100 m，ρC=200 Ω·m，ρU=200 Ω·m，ρD=200 Ω·m，rT=3.65 cm，rB=4～20 cm，d=rB?rT(儀器始終位于鉆孔底部)，ρm=0.1(水)、107(空 氣) Ω·m，f=0.1、0.4、2.0 MHz，儀器保持水平，不同井眼半徑時的方位電磁波測量結果如圖5 所示，可以看出，當鉆孔中為空氣時，幅度比信號受鉆孔直徑的影響可以忽略不計，當發射頻率為2 MHz、源距為0.558 8 m 和0.863 6 m 時，相位差信號受鉆孔直徑影響較大；隨鉆孔半徑的擴大，方位電磁波受鉆孔影響增大，幅度比在鉆孔直徑小于14 cm 時受鉆孔影響較小，無需做鉆孔影響校正，相位差在鉆孔直徑超過一定值(0.4 MHz 時鉆孔半徑超過6 cm，2.0 MHz 時鉆孔半徑超過4.5 cm)后需要做鉆孔影響校正；在模型設置的鉆孔半徑范圍內，源距越小，受鉆孔影響越大。

圖5 儀器位于鉆孔底部時鉆孔半徑的影響Fig.5 Influence of borehole radius when instrument is located at bottom of the well hole

3 起伏地層

為了方便計算方位電磁波對煤層邊界的響應特性，在理論研究時往往忽略了地層的起伏形態，導致理論計算模型與實際地層模型存在一定的差異，因此，有必要建立起伏地層邊界，考察其形態特征對探邊特性的影響程度。建立如圖6 所示的地層模型，其中X軸為水平方向(X軸位于起伏地層ZS=0 的位置)，Z軸為豎直方向(Z 軸穿過起伏地層幅度最高值點)，Y軸垂直紙面向里，ρC為煤層電阻率，ρD為底板電阻率，D為儀器中心距X軸距離，A為地層起伏的幅度，T為地層起伏周期，f為發射頻率。地層起伏界面公式由下式產生：

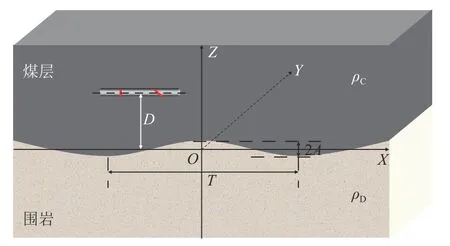
圖6 起伏地層模型Fig.6 Undulating formation model

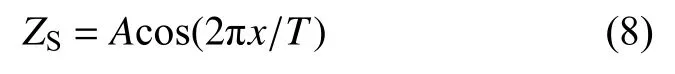
式中：ZS為起伏地層界面與XZ平面交線。

3.1 地層界面起伏幅度響應

在如圖6 所示的起伏地層模型中，設置參數：ρC=200 Ω·m，ρD=10 Ω·m，D=1 m，A=0.05、0.25、0.50 m，T=50 m，f=0.4 MHz。儀器沿X 軸方向移動的測量響應如圖7 所示，可知地層界面與儀器相對夾角在儀器橫向移動時雖不斷變化，但方位電磁波測量響應信號仍能反映地層的起伏變化，0.558 8 m 和0.863 6 m 信號探邊距離較小，在常用閾值情況下，無法探測距離界面中心距離1 m 的地層起伏變化(其探邊距離小于1 m)，2.133 6 m 和2.438 4 m 源距的線圈系探邊距離大于1 m。2.133 6 m 和2.438 4 m 信號對地層起伏幅度為A=0.05 m 的地層(地層總起伏0.1 m)，其響應信號的變化在10%左右(測量響應變化常用閾值也為10%)，地層0.1 m 的起伏是該正演條件下儀器測量信號能夠分辨的最小值。

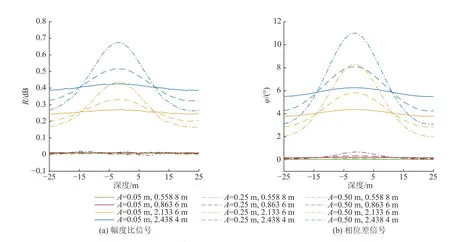
圖7 起伏地層幅度影響Fig.7 Influence of undulating formation amplitude

3.2 起伏地層幅度探測能力分析

在如圖6 所示的起伏地層模型中，設置參數：ρC=200 Ω·m，ρD=10 Ω·m，D=2、3 m，A=0.05 m，T=50 m，f=0.4 MHz。其模擬結果如圖8 所示，可知在地層起伏變化較小時(起伏0.1 m)，使用幅度閾值0.25 dB和相位差閾值1.5°，在儀器與X軸距離D=2 m 時，0.4 MHz 發射頻率的幅度比響應信號小于0.25 dB，無法反映界面幅度變化，但2.438 4 m 源距相位差信號響應值大于1.5°，其探邊距離大于2 m，能夠反映界面起伏變化。在0.4 MHz 發射頻率、儀器與X軸距離D=3 m 時，各源距的幅度比和相位差信號都無法反映界面的起伏變化。

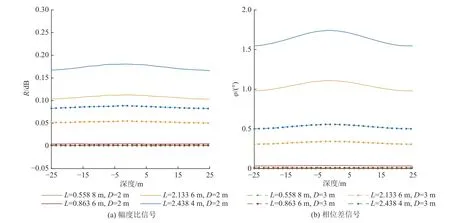
圖8 儀器與地層界面距離的影響Fig.8 Influence of distance between instrument and formation interface

3.3 儀器穿過起伏地層界面響應

在如圖6 所示的起伏地層模型中，設置參數：ρC=200 Ω·m，ρD=10 Ω·m，D=0 m，A=0.5 m，T=50 m，f=0.4 MHz。正演模擬結果如圖9 所示，幅度比和相位差信號在穿過界面時出現極大值，0.558 8 m 和0.863 6 m源距的幅度比信號對模型設置的界面響應值較小，無法反映界面變化，但2.133 6 m 和2.438 4 m 源距測量響應大于閾值，能夠反映界面變化；相位信號所有源距都對界面變化有所響應，可知相位差信號的適應范圍較幅度比信號廣。

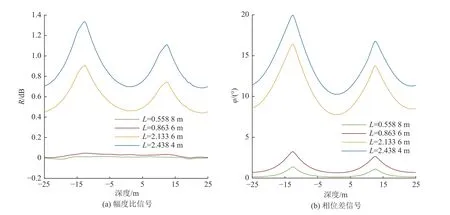
圖9 儀器穿過起伏地層界面響應Fig.9 Instrument response through an undulating formation interface

4 采空區

為研究方位電磁波對采空區的探測性能，建立如圖10 所示的采空區地質模型，其中采空區為長方體形狀，ρC為煤層電阻率，ρG為采空區電阻率，LG=10 m、W=4 m、HG=4 m 分別為采空區的長、寬和高。

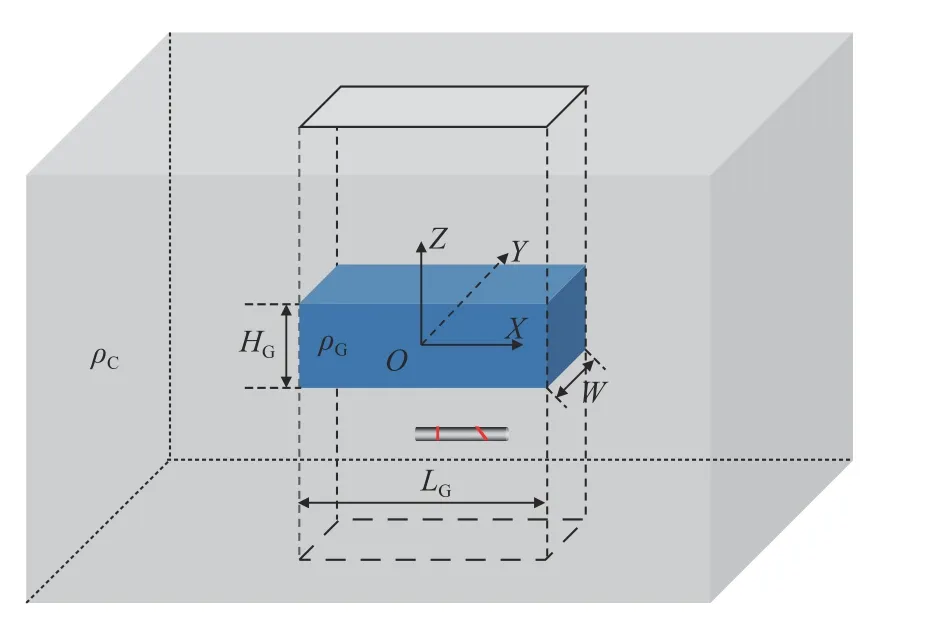
圖10 采空區地質模型Fig.10 Geological model of goaf

4.1 儀器穿過采空區響應對比

設置地層模型參數為：ρC=200 Ω·m，ρG=0.1、1、1 000 Ω·m，f=0.1、0.4、2.0 MHz。模擬計算時儀器保持水平沿Z 方向移動的測量曲線如圖11?圖13 所示。

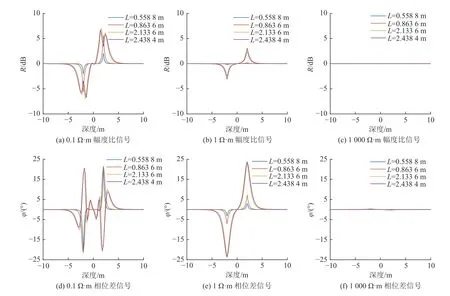
圖11 頻率0.1 MHz 時儀器縱向移動采空區測量響應對比Fig.11 Comparison of measement response of instrument moving longitudinally in goaf at the frequency of 0.1 MHz

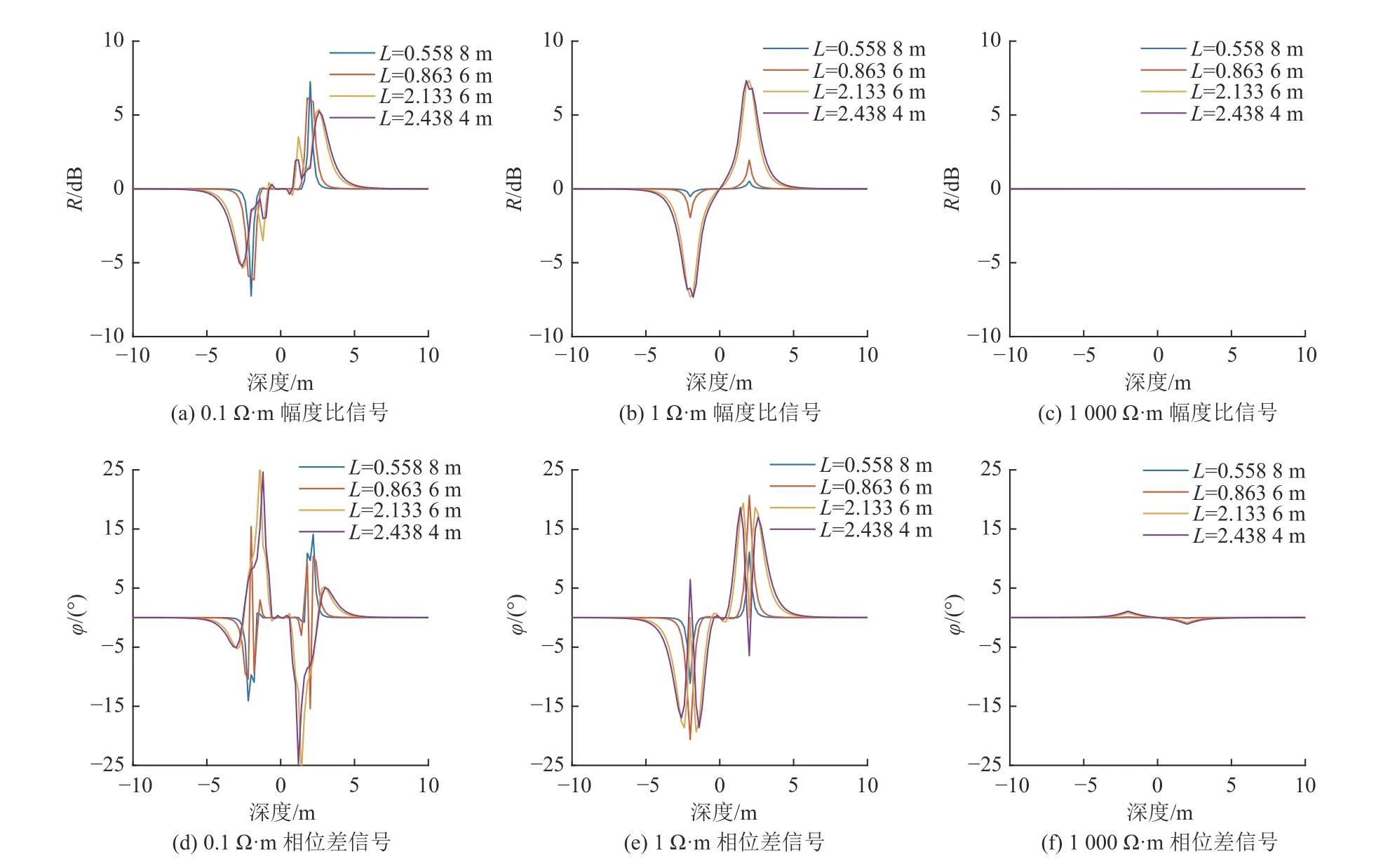
圖12 頻率0.4 MHz 時儀器縱向移動采空區測量響應對比Fig.12 Comparison of measurement response of instrument moving longitudinally in goaf at the frequency of 0.4 MHz

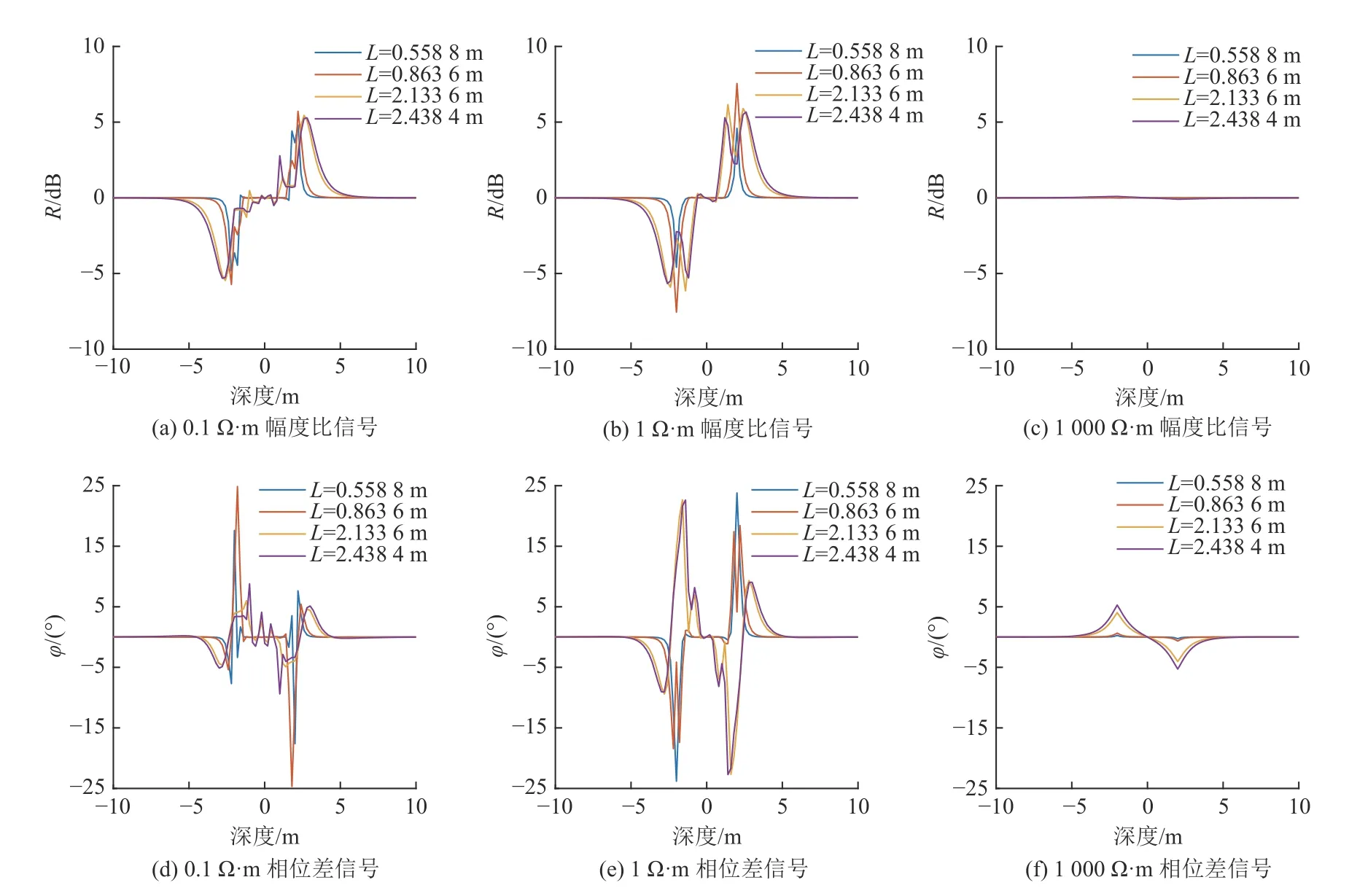
圖13 頻率2.0 MHz 時儀器縱向移動采空區測量響應對比Fig.13 Comparison of measement response of instrument moving longitudinally in goaf at the frequency of 2.0 MHz

可以看出：

(1) 在采空區電阻率為0.1 Ω·m 時，幅度比和相位差響應信號在界面處出現了震蕩，且頻率越高、源距越大震蕩越強，低頻、短源距組合較適合測量低阻采空區，高頻、長源距雖能對低阻采空區進行測量，但其定量解釋存在一定困難；

(2) 在采空區電阻率為1 Ω·m 時，發射頻率為0.1 MHz 時，各源距的幅度比和相位差在巖性邊界處的信號較為理想(如圖10a、圖10e)；隨著頻率的增加，2.133 6 m 和2.438 4 m 源距的幅度比和相位差曲線開始出現震蕩，因此，長源距適合在低頻時進行測量；

(3) 在采空區電阻率為1 000 Ω·m 時，幅度比和相位差對巖性邊界不敏感，其在0.1 MHz 和0.4 MHz 發射頻率的測量響應值均低于幅度比0.25 dB、相位差1.5°的閾值，相位差響應信號對高阻巖性界面的敏感度高于幅度比信號。隨頻率的增加，方位電磁波響應信號幅值增大，相位差在2 MHz 發射頻率時能夠測量高阻邊界，對高阻邊界的探測可用幅度比和相位差聯合分析。

綜上所述，方位電磁波不同源距、頻率的測量信號，對采空區電阻率的適用范圍不同，低發射頻率和短源距適合探測低阻采空區，高頻長源距適合探測高阻采空區。

4.2 儀器未穿過采空區響應

設置地層模型參數為：ρC=200 Ω·m，ρG=0.1、1、1 000 Ω·m，f=0.4 MHz。儀器縱向深度為Z=3 m，模擬計算時儀器保持水平沿X方向移動，測量曲線如圖14 所示，當采空區電阻率為0.1 Ω·m 和1 Ω·m 時，幅度比和相位差信號均有響應，幅度比信號隨采空區電阻率的減小而增加，但相位差信號在采空區電阻率為0.1 Ω·m 時的響應值小于在1 Ω·m 時，可知幅度比信號對低阻異常體更敏感；在采空區電阻率為1 000 Ω·m時，幅度比和相位差信號均較小，無法反映高阻采空區巖性界面。

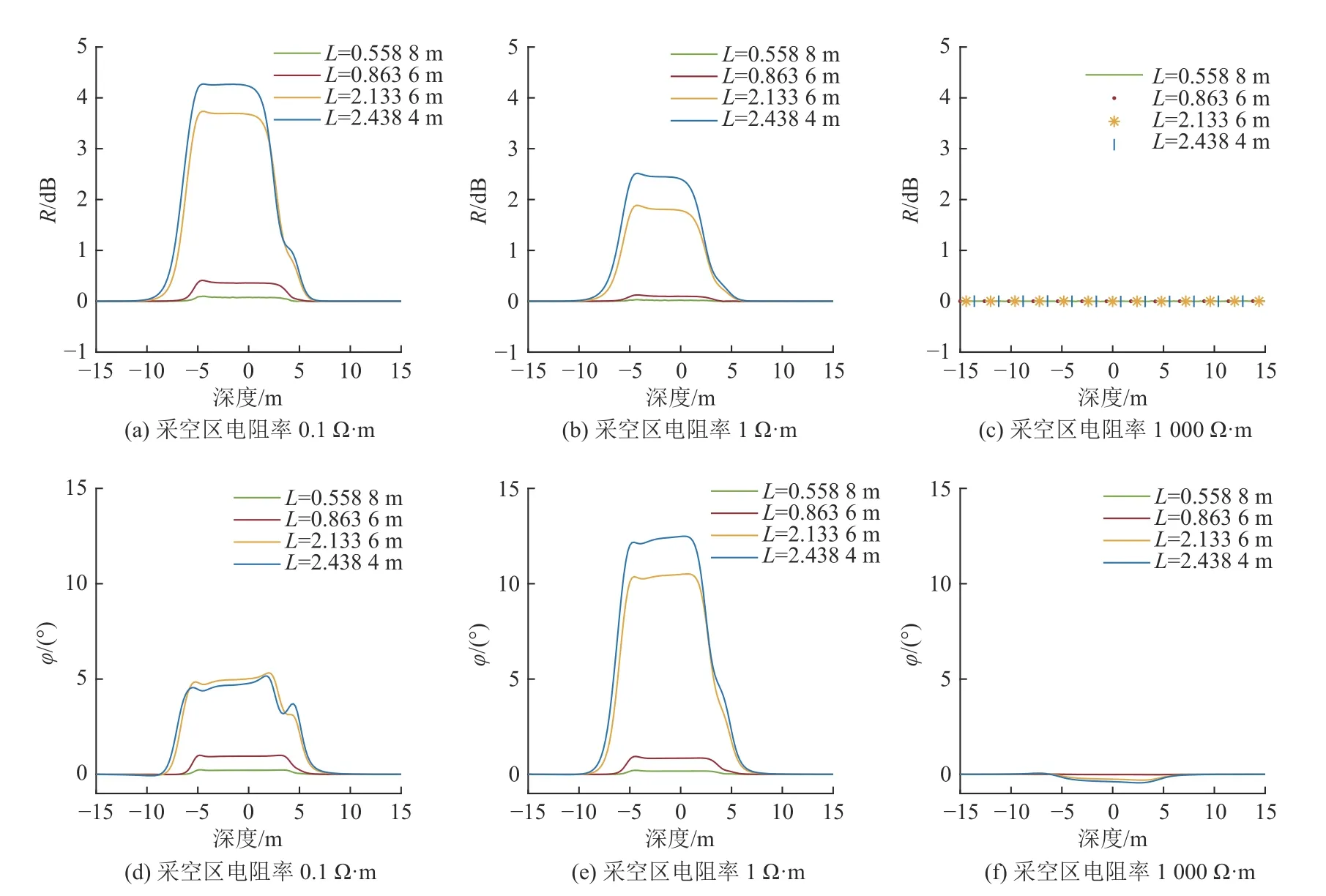
圖14 頻率0.4 MHz 時儀器橫向移動采空區測量響應對比Fig.14 Comparison of measurement response of instrument moving laterally in goaf at the frequency of 0.4 MHz

5 結 論

a.對煤礦井下常見的干孔測量工況，鉆孔流體對方位電磁波測量響應的影響較小，可以忽略不計；當鉆孔中為低阻水時：在直徑100 mm 的孔中，73 mm 直徑的方位電磁波儀器在居中時受鉆孔流體的影響可以忽略；鉆孔對方位電磁波測量響應的影響隨偏心距的增加而增加，儀器偏心時在鉆孔直徑大于9 cm 時需要對地質信號進行鉆孔影響校正。

b.在本文模擬的模型條件下，方位電磁波能夠反映10 cm 的地層起伏變化，長源距的信號對地層起伏敏感度要高于短源距信號。

c.方位電磁波地質信號對低阻采空區較為敏感，但不同源距和發射頻率的電阻率適用范圍不同，應用時需根據電阻率測量值選取相應頻率和源距的數據進行解釋；當采空區為高阻時，需要采用高發射頻率(如2.0 MHz)下的相位差信號進行探測。