一種基于遞歸殘差的回歸模型變點檢驗

秦瑞兵，趙姣

（山西大學 數學科學學院，山西 太原 030006）

0 引言

變點問題最初由Page［1］提出，由于變點問題可以快速地監測到系統在任意時刻出現的變點并發出預警，避免決策上的失誤，對減小損失，降低風險具有重要意義，因此從最初的產品質量控制領域逐步擴展到金融、氣候、流行病學、信號過程和智能導航等領域。Küchenhoff等［2］用帶有變點的趨勢回歸模型對時間序列進行分析，進而估計德國新冠病毒某一天發病的病例數。Basalamah等［3］研究了線性回歸模型下的正態分布誤差在檢測回歸參數變化時的情形，提出一種基于修正信息準則的檢測方法來定位變點，該程序應用于美國國家航空航天局的數據來說明探測過程。

陳希孺［4］與Perron等［5］介紹了有關變點理論的研究與發展。Li等［6］針對分段平穩向量自回歸過程，提出了一種三步法檢測多重結構突變，用于多元時間序列變點估計。Shi等［7］用基于秩的回歸方法對于多變點連續分段線性回歸模型去同時估計回歸系數和閾值的位置，實現了魯棒性。Lu等［8］將模糊變點算法與M估計相結合實現了回歸模型中的變點和回歸參數的魯棒估計。Brown等［9］提出了在變點理論廣為應用的CUSUM統計量和CUSQ統計量。Sen［10］導出基于遞歸殘差的CUSUMrec統計量的極限分布為一個加權維納過程的最大值，即使回歸模型的自變量包含因變量滯后項滯后，該統計量的極限分布仍然正確，Ploberger和Kr?mer［11］考慮用最小二乘回歸殘差代替遞歸殘差構造了CUSUMols統計量，此統計量除了在變點發生時刻靠前的情形功效并不高之外，相較于CUSUMrec統計量，對于變點發生時刻靠后的情形功效有較大提高。對此Brown［9］基于遞歸回歸殘差平方序列，構造 CUSQrec統計量，Ploberger和 Kr?mer［12］導出了 CUSQrec統計量的極限分布。Deng與Perron［13］在一般混合條件下得到了CUSQrec統計量和CUSQols統計量的極限分布，對文獻［12］CUSQ統計量的極限分布做了系數修正，得到CUSQ統計量的極限分布為一個布朗橋過程的最大值。Ploberger和Kr?mer［14］考慮了CUSUM統計量和CUSQ統計量的局部勢函數，得出CUSQ統計量有很小的漸近局部勢而CUSUM統計量有較大的漸近局部勢，除非變點的系數偏移量正交于解釋變量的均值向量，但由于局部性質對于發生較大偏移的情形并不適用，Deng與Perron［5］考慮了CUSUM統計量和CUSQ統計量的非局部勢函數的性質，表明CUSQ統計量在非局部的情形下有較高的功效。基于以上方法，Nielsen和Sohkanen［15］將CUSQ檢驗統計量推廣到具有確定性時間趨勢的非平穩自回歸分布滯后模型，將漸近理論更廣泛地應用于最小二乘殘差的檢驗。

但是當變點發生時刻靠前時，遞歸殘差的CUSQ檢驗功效較低。本文將遞歸殘差序列分為兩組，比較兩組遞歸殘差平方的算術平均值，構建檢驗統計量，推導其漸近分布，并得到其在備擇假設下的漸近極限。模擬結果表明本文構造的檢驗統計量比已有統計量在變點發生時刻靠前的情形功效有較大提高。

1 模型與假設

2 主要結論

3 數值模擬

本節通過數值模擬來分析本文所給方法的有限樣本性質，并與文獻［5］中的方法進行比較。首先生成120個獨立同分布的標準正態隨機數，代入統計量（5）中，重復該試驗5 000次，可以計算得到顯著水平α=0.05的臨界值為8.470 2。為方便與文獻［5］比較，考慮用模型（1）生成數據：xt={x1t，x2t}={1，(-1)t}′，備擇假設中系數 βt的變化由 δ=b[cos(φ)，sin(φ)]′來確定，其中 φ 是 δ和 xt的均值向量的夾角，分別取值為 φ=0?，45?，90?，λ取 0.3，0.5，0.7，ut為標準正態隨機數列。表1上部分為文獻［5］中的實驗結果，下部分為本文中方法重復試驗5 000次中統計量拒絕原假設頻率保留兩位小數的結果。對比表1上下兩部分，可以看到：（1）本文構建的統計量在原假設成立時，其經驗水平更接近檢驗的顯著水平0.05；（2）當變點發生在序列早期時，本文的統計量比傳統的基于遞歸回歸殘差的CUSQ統計量具有較高的功效。當變點發生在序列后期時，本文方法的功效也均高于或等于已有基于遞歸回歸殘差的CUSQ統計量。這與定理2的結論相吻合。

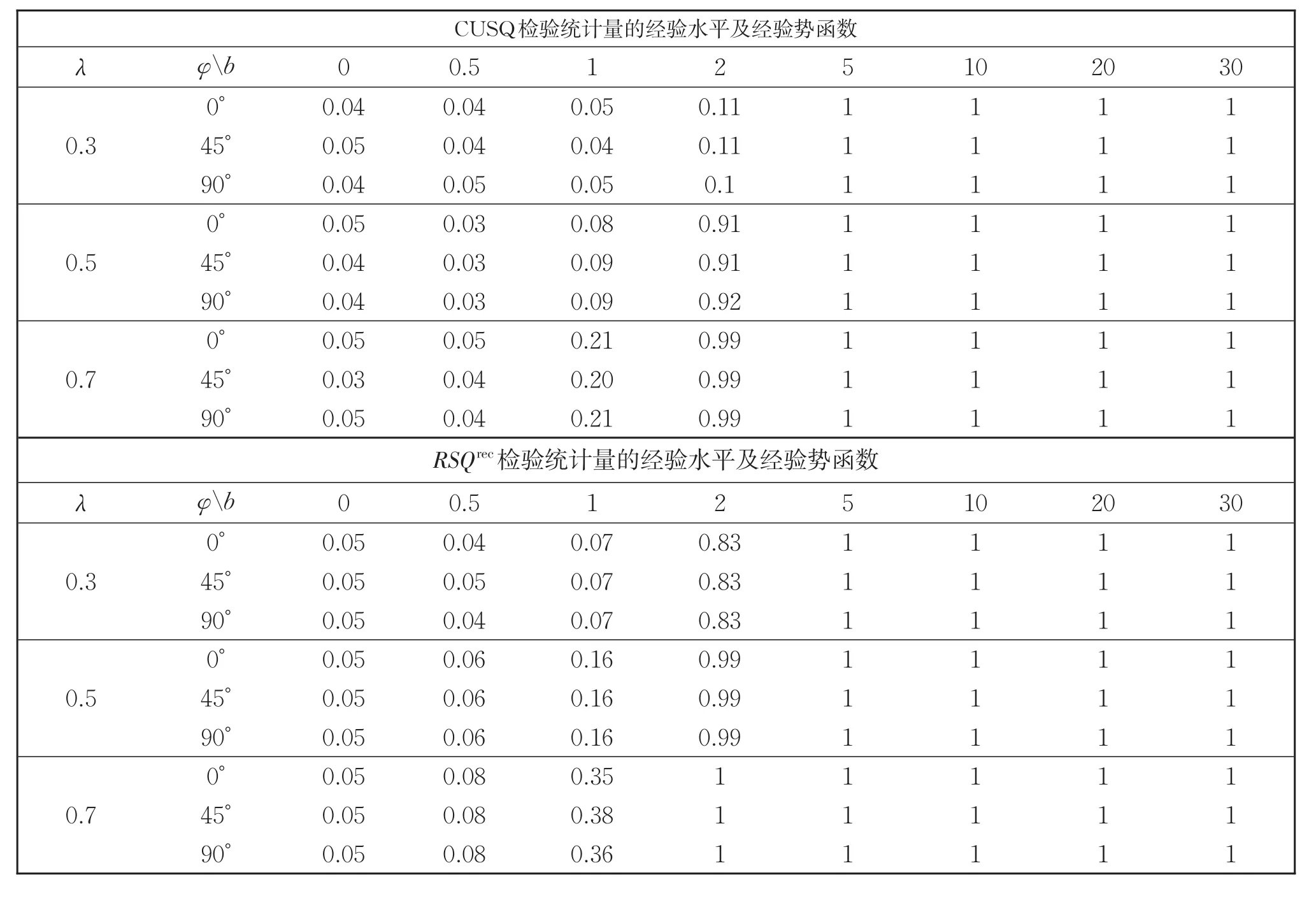
表1 檢驗統計量的功效Table 1 Power of the test statistics

4 結論

本文所構造的統計量對犯第一類錯誤的概率與選定的顯著水平0.05更接近，同時，在檢驗有限樣本下有更高的功效。在變點發生時刻靠后的情形下，功效也逐漸趨于1，對于變點發生時刻靠前的情形，較已有統計量有更高的功效。

但本文僅考慮誤差為正態分布的情形，未考慮誤差為非正態分布的情形以及誤差具有相依性的情形。如何基于遞歸殘差和最小二乘回歸殘差構造適合于誤差是非正態分布和誤差之間具有相依性情形下線性回歸模型系數變點檢驗問題上，有待進一步研究。