千米級大跨公鐵兩用懸索橋結構特性及剛度指標研究

陳進昌,雷俊卿,金 令,胡 春

(1.中鐵工程設計咨詢集團有限公司,北京 100055； 2.北京交通大學,北京 100044； 3.中冶南方城市建設工程技術有限公司,武漢 430062)

引言

隨著渤海海峽、臺灣海峽、瓊州海峽通道的建設提到議事日程，研究和發展鐵路大跨度橋梁滿足鐵路公路跨江通海交通要求勢在必行，而大跨度公鐵兩用懸索橋是千米級大跨度橋梁考慮的首選橋型。

大跨度公鐵兩用懸索橋的設計研究尚有大量復雜技術問題需要攻關，相關的結構特性深化研究工作需要加速持續展開，包括大跨度懸索橋合理結構形式與尺寸、橋梁跨度優化、超長主纜合理結構參數、橋塔基礎形式與材料參數、車橋振動、抗風、抗震、抗海浪和防撞等重要技術問題的研究。

由于鐵路列車活載大、運行速度高及列車運行穩定性和旅客舒適性要求高等特點，對于大跨度公鐵兩用懸索橋除具有合理的結構受力體系，較好的抗風、抗震性能外，還需具有較大的豎、橫向剛度。

由于懸索橋結構的特殊性和大跨度橋梁剛度限值的定量上仍然缺乏足夠的實踐與研究，各國對大跨度鐵路橋梁尚缺少相應的規范，橫向及豎向剛度缺乏明確的限值標準，可以參考的規范都是建立在中小跨度橋梁動力分析和實測試驗基礎上的。對于活載體系，我國現行的規范針對鐵路橋梁活載中的豎向靜活載、動力系數和沖擊系數等指標有著明確的數值，但均未對鐵路及公鐵兩用懸索橋涉及的參數進行明確的規定。

通過改變大跨度懸索橋結構參數(邊中跨比、垂跨比、高跨比、寬跨比、支承體系)，對比分析它們對懸索橋豎向剛度、橫向剛度的影響敏感性，總結出有效的剛度提高措施，并對垂跨比等進行技術經濟分析意義重大。

1 大跨度鐵路懸索橋結構剛度評價指標體系

1.1 鐵路橋梁剛度評價指標體系

隨著我國鐵路建設技術的不斷發展，橋梁的跨度和結構形式已經超過了現有橋梁的設計跨度和規范的適用條件，所以剛度的評價方法和限值問題需要重新審視。國內外許多機構的專家學者對此做了廣泛而深入的研究，取得了豐碩的成果，這些成果反映在各規范的條文中。但是，評價指標各不相同，寬嚴程度差異較大。

鐵路橋梁作為列車軌道支撐結構，在橫向和豎向都應有一定的剛度，以保證列車運行安全，正常通過。所謂安全通過就是指列車通過橋梁時不脫軌，橋梁保持其承載能力；所謂正常通過就是指列車能按照設計速度通過橋梁。剛度評價指標體系主要有：Sperling指標、Janeway指標、脫軌系數、輪重減載率、車體振動加速度、豎向和橫向撓跨比、轉角、橋梁振動加速度、寬跨比、自振頻率等[1]。

1.2 國內外已建成運營的大跨度鐵路懸索橋剛度值

公鐵兩用大跨懸索橋大多都是雙鉸(簡支)懸索橋及單跨懸吊的橋梁。它們與連續的懸索橋相比，作用于加勁梁的彎矩較小，因而截面也較小，一般來說是比較經濟的，然而，日本本四聯絡線上的懸索橋是高速列車行駛的公鐵兩用橋，因而要盡量減小加勁梁的撓度與轉折角以及伸縮量。北備贊瀨戶大橋采用變形形狀優越的3跨連續懸索橋，而下津井瀨戶大橋則采用附帶伸出跨的單跨懸吊懸索橋。

日本代表性公鐵兩用懸索橋剛度見表1[2-4]。

表1 日本已建公鐵兩用懸索橋剛度

1.3 國內外對大跨度鐵路橋梁剛度限值的初步研究成果

日本本四聯絡橋公鐵兩用懸索橋允許折角標準：當車速160 km/h時，豎向折角5‰，水平折角2.5‰。

西南交通大學張東碩士通過分析已建橋梁的橫豎向撓跨比，提出不同車速下的撓跨比、梁端轉角建議值，見表2。

1.4 大跨度鐵路懸索橋剛度評價指標及其建議值

(1)車輛運行安全及舒適度評價指標體系

車輛平穩性(舒適性)指標、脫軌系數、輪重減載率、車體振動加速度按現行規范[6]。

(2)橋梁豎向剛度建議限值

鐵路懸索橋豎向剛度建議值見表3。

表3 豎向撓跨比和轉角建議值

(3)橋梁橫向剛度建議限值

鐵路懸索橋橫向剛度建議值見表4。

表4 橫向撓跨比和轉角建議值

這里的撓跨比和橫向轉角的建議值需要以車輛運行的評價指標為標準，通過大量的車橋耦合分析來驗證其合理性，并通過實踐來驗證其可靠性。如果做車橋分析來驗證撓跨比和轉角的建議值合理性時，建議將客車和貨車分開，使用不同的限值。

除了上述指標，還可輔以錯位、曲線半徑、自振周期、振幅等指標來保證鐵路懸索橋技術的可行性[1]。

2 結構方案

考慮懸索橋活載占比小，研究對象為大跨度公鐵兩用懸索橋，擬定主跨1196m，邊跨可布設橋墩。根據建橋條件，大橋設計為單跨懸索橋，主纜跨度布置為(300+1196+300)m，主纜矢跨比1∶10。該懸索橋采用鋼桁加勁梁，跨度布置為(78+104+1196+104+78)m，主跨采用吊索懸吊，邊跨無吊索。方案總體布置如圖1所示。

圖1 懸索橋方案總體布置(單位：m)

公鐵兩用懸索橋采用雙層橋面布置，下層四線鐵路，上層六車道公路。大跨度鋼桁梁多采用2～3片主桁。兩片主桁較為經典，多數公路橋梁與單、雙線鐵路橋梁采用此種方式。近年我國建成了較多的公鐵、鐵鐵合建橋梁，這些大型橋梁的鐵路線路數量多為四線，主梁結構以鋼桁梁為主，橫橋向多采用3片主桁結構，以減小橫梁跨度，縮小橫梁尺寸，提高橋面剛度。設置3片主桁，有利于橋面系構造布置，橫向剛度優異，適合較高速度列車運行。3片主桁適宜在梁式橋與大跨度斜拉橋中應用，梁式橋可設置數量相當的支座/墩臺，大跨斜拉橋可設置3個索面，對應3片主桁來傳遞荷載。而目前懸索橋設計均采用雙主纜布置(四主纜布置的也是每兩根布置在一側)，考慮傳力對稱性，雙主桁結構與懸索橋的匹配性優于三主桁。本橋最終選擇雙主桁結構。

根據懸索橋加勁梁均勻受力特性，本橋選擇采用帶豎桿的華倫式桁架，可利用豎桿位置設置吊點，用于連接吊索。同時，本橋采用雙主桁形式，兩主桁間距較大，需要設置較強的橫聯，華倫式桁架便于設置橫向連接系。

為便于鐵路橋面布置，同時降低制造安裝難度，最終斷面形式采用上下層同寬的直立主桁截面[7-8]，桁寬同主纜間距，吊索垂直布置，連接主纜與主桁。主梁橫斷面布置如圖2所示。

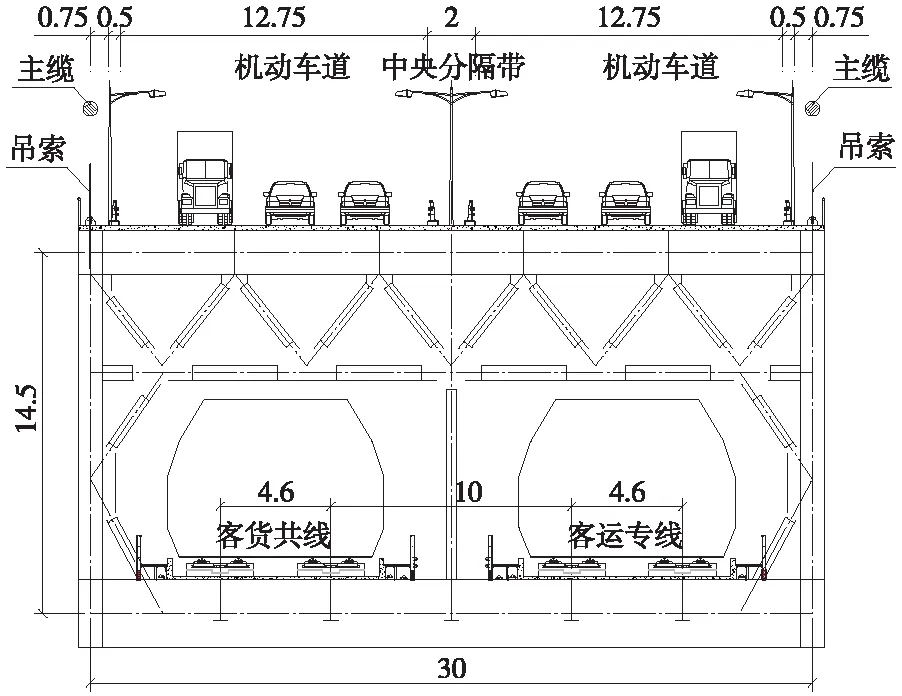
圖2 主梁橫斷面布置(單位：m)

(1)技術標準

①線路等級：Ⅰ級鐵路雙線(按高速鐵路、城際鐵路、客貨共線鐵路和重載鐵路分別加載)；

②行車速度：200 km/h；

③橋面坡度：兩端各設1.5%縱坡，跨中為豎曲線頂點；

④活載標準：ZK、ZC、ZKH、ZH活載[9]；

⑤基本風速：運營階段設計重現期100年，V10=30 m/s；

(2)設計指標

①主纜跨徑：中跨1 196 m，邊跨300 m(無吊索)；

②矢 跨 比：1/10；

③主纜中心距：30 m；

④主纜直徑：等效直徑1 000 mm，抗拉強度1 860 MPa；

⑤吊索直徑：等效直徑140 mm(兩股騎跨式，單股直徑100 mm)，抗拉強度1 670 MPa，間距13 m；

⑥索塔高度：180 m(承臺頂面以上)；

⑦加勁梁：高度14.5 m，寬度30 m，節間距13 m。加勁梁和二期恒載沿橋長方向約800 kN/m。

3 設計活載

對于撓度較大的鐵路懸索橋來說，由撓度產生的軌道坡度將形成列車行駛的障礙，按照影響線加載計算時的布載形式與實際的交通狀態不符合而形成非常大的活載，由此產生的結果是不經濟和不合理的。圖3為中跨撓度最大點的影響線圖式，如果按照影響線加載，加載的長度要明顯長于實際列車的長度。因此有必要根據列車的實際車長度，或者利用車站到發線長度作為車輛加載的力學模式，在連續發生有撓度的軌道上模擬車輛行為。

圖3 撓度最大點的影響線圖式

因此，本節模擬車輛長度取500 m，按照中-活載圖式截取，取值為81.72 kN/m。

我國的中-活載是根據當時我國鐵路系統機車、車輛運用情況，按不同的列車編組，對不同跨度簡支梁所產生的荷載效應的包絡線，通過幾種具有代表性的活載圖式的分析對比，從中選定的列車活載標準圖式。對于大跨度橋梁，有必要確立能反映實際交通狀態的合理的活載體系。因此，將中-活載換算成均布荷載作用在大跨度橋梁上的合理性有待進一步研究。

另外，沖擊系數是表示橋梁動力撓度或動態應力比相應靜力值增加的比例，原有規范都是針對簡支梁或連續梁等跨度較小的橋型[10]，所以沖擊系數的選取也需要進一步調查分析研究。日本規范對此做了如下解釋：對于懸索橋來說，列車的質量與懸索橋的質量相比是小的，軌道上如果使用直接緊固在鋼梁的長鋼軌時，估計除了列車的速度效果之外，忽略其他因素也不會有很大的差別，在列車行駛對橋梁產生的動力效果中，豎直方向的影響估計在設計中只需用沖擊系數來反映即可。參考日本在懸索橋的加勁梁及吊索設計時所用的新干線沖擊系數，暫選取沖擊系數1.12。

根據TB 3466—2016《鐵路列車荷載圖示》，計算橋梁在雙線高速鐵路、城際鐵路、客貨共線鐵路和重載鐵路(計算時荷載系數Z=1.2)4種不同類型線路荷載下的結構反應。圖4～圖7分別反映了在不同荷載類型下的主梁跨中撓度、主纜應力、吊索應力和跨中上下弦桿的應力。

圖4對比了4種列車荷載作用下的主梁跨中豎向撓度，從圖中可以看出，雙線重載鐵路荷載作用下主梁跨中豎向撓度最大，撓跨比約為1/500，城際鐵路下撓度最小，撓跨比約為1/1 000。

圖4 不同列車荷載下主梁跨中撓度

圖5對比了不同列車荷載下主梁跨中上下弦桿的應力，在雙線重載鐵路荷載下，上弦桿應力為57.8 MPa，下弦桿應力為85.6 MPa，斜桿應力為98.0 MPa。

圖5 不同列車荷載下主梁跨中上下弦桿應力

圖6對比了不同列車荷載下主跨部分主纜的應力，在雙線重載鐵路作用下主纜應力由跨中的880 MPa變化到960 MPa。

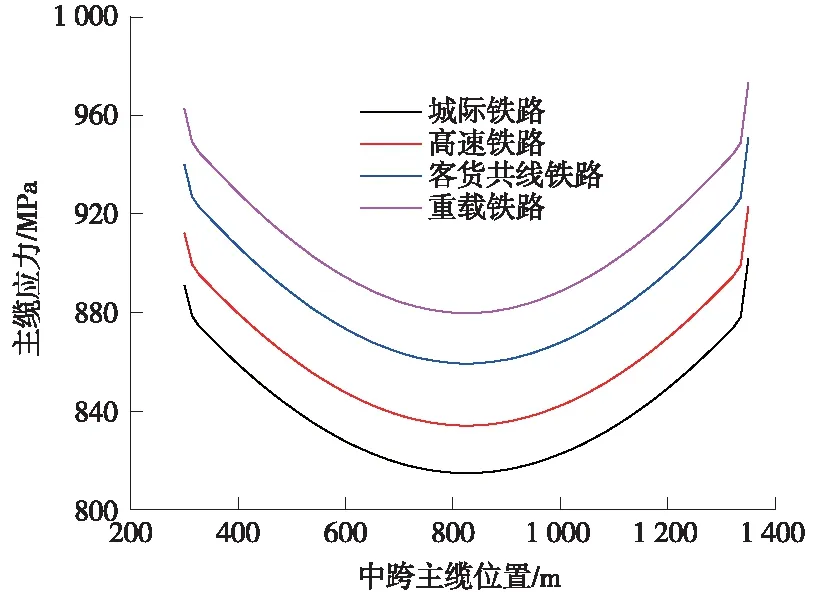
圖6 不同列車荷載下主纜應力

圖7對比了不同列車荷載下吊索的應力，在雙線重載列車荷載下，吊索應力由跨中的655 MPa變化到塔根部924 MPa。

圖7 不同列車荷載下吊索應力

結合本公鐵兩用懸索橋參數與我國高速重載鐵路現狀，參照大秦鐵路的實際運營情況對模型進行移動荷載的加載，與上述按照TB 3466—2016《鐵路列車荷載圖示》[9]進行加載的結果進行對比。

大秦鐵路是中國第一條雙線電氣化重載運煤專線，是中國西煤東運的主要通道之一，其運行的2萬t載重的重載列車長度達2 700 m，均布荷載約為72.6 kN/m，而已經進行試驗的3萬t載重的重載列車長度達到3 971 m，均布荷載為75.6 kN/m。因此，結合本公鐵兩用懸索橋的具體情況，在移動荷載加載時，算例按加載長度為全橋長度加載，集中荷載按照《鐵路列車荷載圖示》[9]取為250 kN，均布荷載取74 kN/m。

按客貨共線鐵路計算結果，橋梁跨中撓度為2.18 m，撓跨比約為1/550；主纜應力在846～912 MPa之間，安全系數約為2.0，需要再加大主纜的直徑或者使用高性能高強鋼材，如抗拉應力達到2 100 MPa；吊索應力在640～690 MPa之間，安全系數約為2.4，吊索也還需要加大直徑或使用高強高性能的鋼材，使安全系數在3～4之間；加勁梁跨中上弦桿應力為48.2 MPa，下弦桿應力為71.3 MPa，斜桿應力81.7 MPa，加勁桁架的應力比較富余。

4 材料設計標準

主纜在索塔頂的主索鞍及錨碇支墩的散索鞍處存在轉向，所以同時也承受彎曲應力；每根主纜都是由若干根鋼絲組成，制造時每根鋼絲的無應力長度都不可避免地存在誤差，而施工工藝也決定了在緊纜后每根鋼絲的松緊程度也不完全一致。由于上述兩個原因(主纜彎曲應力及受力不均勻性)，懸索橋主纜的安全系數一般取2.2～2.5。

吊索[11-13]主要有如下兩種形式：騎跨過索夾的鋼絲繩吊索(由若干根直徑不同的細鋼絲編制而成)和預制平行鋼絲吊索(有若干根直徑相同的平行鍍鋅鋼絲組成)。鋼絲繩和平行鋼絲吊索，安全系數分別取為4.0和3.0。

5 大跨度公鐵兩用懸索橋結構靜力特性參數研究

以矢跨比1/10，加勁梁梁高15 m，梁寬30 m為例，建立公鐵兩用懸索橋有限元基本計算模型，進行靜力計算分析。然后通過變化懸索橋的梁高、梁寬、邊中跨比、垂跨比、約束條件等，按中荷載作用分析這些參數對懸索橋豎橫向剛度的影響[14]。

5.1 不同支承體系對橋梁剛度的影響

懸索橋按照結構體系特點進行分類，可以分為如圖8所示的8種類型。

圖8 懸索橋結構體系

單跨雙鉸體系常見于高山峽谷地區或者主塔已達河流岸邊，兩側橋梁直接搭建在輔助墩上更為經濟，或者由于路線線型限制，橋梁邊跨為曲線，不能與主纜平行，無法使用吊索的情況[15-16]。

三跨雙鉸體系懸索橋和三跨連續體系懸索橋是世界上最常見也是應用最廣泛的懸索橋類型。由于此類結構受力較為合理，特別適用于大跨度懸索橋建設。

多跨連續體系懸索橋為多塔多跨結構(如武漢鸚鵡洲大橋)，由于主梁長度大，結構較柔，因此自振周期較長。為了提高橋梁的整體剛度，索塔的順橋向剛度以及主纜的垂跨比需要增加[17-19]。

自錨式體系懸索橋區別于地錨式懸索橋，是將主纜直接固定在邊跨加勁梁上，由于主纜產生的水平分力需要與加勁梁的軸向壓力相平衡，所以這就要求自錨式懸索橋的主梁必須是連續的[20]。

懸索橋支承體系的選擇需要綜合橋梁的功能、規模、建設條件、地理條件以及經濟性等各類因素確定，并結合相應的支承方式、附屬構造設施等，以滿足橋梁整體的剛度要求。本文將研究不同支承體系對懸索橋剛度的影響程度，從而合理選擇懸索橋支承體系。本文對比的支承體系分別是單跨帶伸出跨[21]、單跨雙鉸、三跨連續懸索橋。

(1)豎向剛度影響分析

在滿布活載的作用下，不同支承體系對應的豎向撓度和豎向轉角包絡圖分別如圖9、圖10所示，其中邊跨長度均為300 m。

圖9 不同支承體系對應的豎向撓度包絡圖

圖10 不同支承體系對應的豎向轉角包絡圖

從圖9、圖10可以看出，在移動荷載作用下，三跨連續體系懸索橋的豎向撓度以及轉角均與單跨帶伸出跨體系結果比較接近，三跨連續體系比其他兩種體系整體豎向撓度大約3%。而單跨雙鉸懸索橋，主跨加勁梁沒有邊跨的約束，最大豎向撓度比其他兩種體系增加約15.6%。可見宜避免采用單跨雙鉸體系，若遇到高山峽谷地區，邊跨較短或者不得不采用單跨雙鉸體系時，加勁梁梁端應增加約束措施。單跨雙鉸比其他兩種體系梁端最大轉角大51.6%，三跨連續與單跨帶伸出跨結果較為接近，加勁梁邊跨部分，三跨連續的轉角略大。綜上，公鐵兩用懸索橋支承體系宜采用單跨帶伸出跨體系。

(2)橫向剛度的影響分析

橋梁橫向剛度通過施加橫向風荷載進行定量分析，如圖11、圖12所示為不同的支承體系下加勁梁橫向變形和橫向轉角包絡圖。

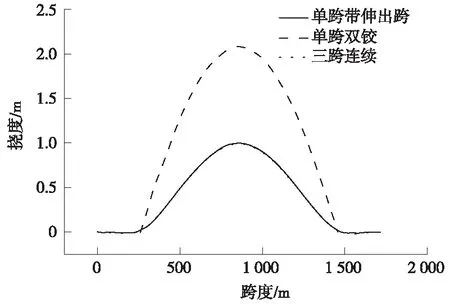
圖11 不同支承體系對應的橫向撓度包絡圖

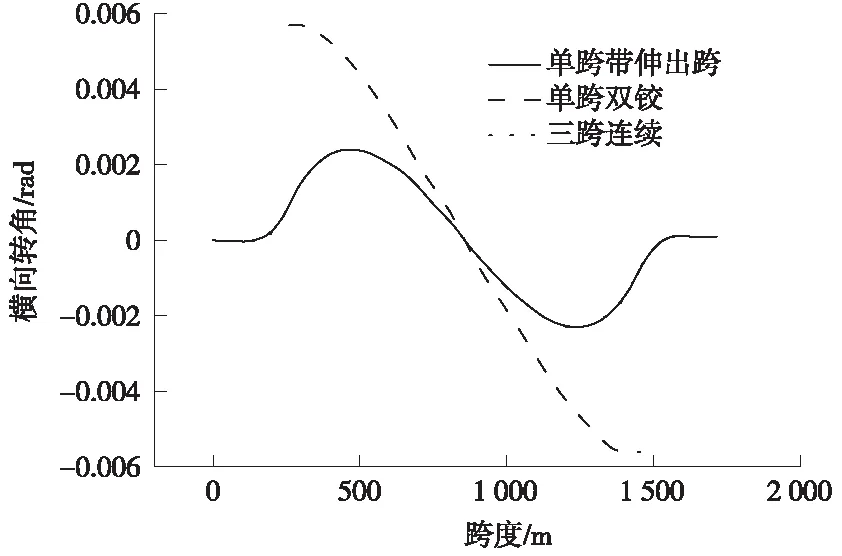
圖12 不同支承體系對應的橫向轉角包絡圖

從圖11和圖12可以看出，三種懸索橋支承體系中，單跨帶伸出跨和三跨連續體系在橫向荷載的作用下的變形和轉角相近，而這兩種支承體系的橫向變形和轉角均明顯小于單跨雙鉸體系，橫向撓度上單跨雙鉸體系會增加110%，橫向轉角增加142%。另外，由于單跨雙鉸體系懸索橋加勁梁梁端橫向約束小，其橫向最大轉角出現在橋塔處，而其他兩種體系最大轉角出現在約1/5跨處。以上結果表明單跨雙鉸體系懸索橋在風荷載作用下表現較差。若懸索橋位置處于風力較大地區，應盡量避免采用單跨雙鉸體系。

結合支承體系對公鐵兩用懸索橋剛度的影響分析可知，單跨帶伸出跨具有和三跨連續幾乎相同優越的豎向和橫向剛度，行車平順性優越，但是單跨帶伸出跨的經濟性更好，因此后續分析的公鐵兩用懸索橋均采用單跨帶伸出跨的支承體系。

5.2 邊跨輔助橋墩布置方式對橋梁剛度的影響

總結不同支承體系對懸索橋的影響，可以得到單跨帶伸出跨體系懸索橋結構特性與三跨連續較為接近，且結構可行性及經濟性較優。

在懸索橋橋型確定采用單跨帶伸出跨體系條件下，通過改變邊跨橋墩布置方式，研究不同的邊跨橋墩布置形式對于懸索橋剛度的影響。邊跨橋墩的布置形式有很多種。為了方便對比，邊跨輔助橋墩布置分為3種形式，分別為104 m、78 m+104 m、78 m×2+104 m。也就是第一個邊跨跨度為104 m，后續增加2個78 m的連續邊跨。在研究過程中，橋梁其他參數保持不變。

(1)豎向剛度影響分析

在滿布活載的作用下，對比不同的連續邊跨數量的橋梁計算結果，邊跨數量對于加勁梁的撓度和豎向轉角的影響很小。也就是說在確定了第一個輔助墩位置的情況下，繼續增加邊跨數量，并不會增大橋梁剛度。而橋梁邊跨跨數增加僅可以影響輔助墩位置處主梁的轉角，綜合考慮，單跨帶伸出跨的邊跨建議采用兩跨形式。

(2)橫向剛度影響分析

在橫向風荷載作用下，邊跨數量的不同對于橋梁橫向剛度來說影響也很小。但是主梁連續的長度增加，可以適當減小風荷載作用下加勁梁的橫向撓度和轉角的減小。

3種邊跨輔助墩的布置形式對公鐵兩用懸索橋的剛度的影響是不同的，但是(78+104) m的計算結果與(78×2+104) m的計算結果相近，差別不大，優越性相同，但(78+104) m這種布置形式更為經濟，后續的分析均采用(78+104) m的輔助墩的布置形式。

5.3 高跨比對橋梁剛度的影響

本節分析的懸索橋梁高分別為13.5，14,14.5 m，對應的懸吊結構重力分別為807,811 kN/m和815 kN/m，垂跨比都采用1/10，梁寬均取為30 m。

在列車活載作用下，隨著梁高的增加，懸索橋的豎向撓度和豎向轉角以及加勁梁的扭轉角均有所減小；最大撓度減小3.26%，跨中豎向轉角減小6.08%，扭轉角減小5.59%，所以適當的加高梁高能增加懸索橋的豎向剛度。后續的分析均按具有較高的14.5 m梁高尺寸進行分析。

5.4 寬跨比對橋梁剛度的影響

寬跨比，即加勁梁寬度與主跨的比值。已建的大跨度懸索橋中，懸索橋加勁梁寬跨比大致在140～160之間。為方便分析對比，選取的主桁桁寬分別為22.5，25，27.5 m和30 m共4種，對應的加勁梁寬跨比分別為1/53，1/48，1/43，1/40。對應的懸吊結構重力分別為780,792,804 kN/m和815 kN/m，垂跨比取為1/10，加勁梁高均為14.5m。

(1)豎向剛度影響分析

在列車活載作用下，不同梁寬對應的豎向最大撓度和中跨跨中的梁部轉角如表5所示。

表5 不同梁高對應豎向最大撓度和中跨跨中梁部轉角

從表5可知，隨著梁寬的增加，懸索橋的豎向撓度和豎向轉角以及加勁梁的扭轉角均有所減小；最大撓度減小4.7%，跨中豎向轉角減小13.1%，所以適當加寬梁寬能增加懸索橋的豎向剛度。

(2)橫向剛度影響分析

在風荷載作用下，加勁梁的寬跨比對于懸索橋橫向的撓度和轉角影響很大。寬跨比越大，橫向撓度和橫向轉角越小。當寬跨比由1/53增加到1/40時，橫向撓度將減小40.5%，橫向最大轉角減小45.7%。

5.5 懸索橋邊中跨比對橋梁剛度的影響

邊中跨比，也就是邊跨與主跨的比值。邊中跨比越大，意味著邊跨跨度越大，邊纜傾斜角度就越小，對應的邊纜內力會減小，懸索橋的剛度也會受到影響。

采用4種不同邊中跨比的懸索橋進行對比分析，為了對比結果明顯，邊跨分別為200，300，400，600 m，對應的邊中跨比分別是1/6，1/4，1/3，1/2。采用單跨帶伸出跨支承體系，邊跨橋墩布置方式采用78 m+104 m，除邊中跨比外，其他參數保持不變。

(1)豎向剛度影響分析

活載作用下，懸索橋減小邊中跨比，加勁梁豎向撓度、豎向轉角在邊中跨位置都減小。豎向撓度呈現向上提的趨勢，即加勁梁的下撓減小，而上拱增加。其中，加勁梁在主跨跨中處的下撓幅度減小最多，而豎向轉角變化不大。邊中跨比由1/2增加到1/6時，加勁梁豎向撓度最多可以減小11.4%，而豎向轉角最多僅減小2.9%。反映出邊中跨比對加勁梁的豎向撓度的影響較大。

(2)橫向剛度影響分析

在橫向風荷載作用下，改變懸索橋的邊中跨比，加勁梁的橫向撓度和轉角的變化都很小，幾乎可以忽略。

5.6 垂跨比對橋梁剛度的影響

垂跨比，即懸索橋主纜在主跨的垂度和主跨的比值。懸索橋主跨確定的情況下，主塔高度決定著垂跨比的大小。增加主塔高度，垂跨比也增加，橋塔施工難度加大，工程量也會增加；若減小懸索橋垂跨比，雖然可以減小主塔高度，但主纜傾斜角度減小，主纜在豎向內力不變的情況下，水平分力將增大較多，主纜截面將會增大。因此選定合理經濟的懸索橋垂跨比十分重要。

懸索橋垂跨比一般適合在1/8～1/12范圍內選取。分別選取垂跨比1/8、1/9、1/10、1/11，分析對懸索橋豎向剛度的影響。

(1)豎向剛度影響分析

在滿布活載的作用下，不同垂跨比懸索橋對應的豎向撓度包絡圖如圖13所示。

圖13 不同跨度對應的豎向撓度包絡圖

從圖13可以看出，隨著垂跨比的減小，懸索橋加勁梁豎向撓度增大，而主跨跨中加勁梁豎向撓度增大最多。隨著邊垂跨比從1/8減小到1/11，加勁梁豎向最大撓度增大約15%。

(2)橫向剛度影響分析

隨著懸索橋垂跨比變小，風荷載作用下的主梁橫向撓度同時減小。垂跨比從1/8減小到1/11，主梁橫向撓度減小11.4%。隨著垂跨比變小，主纜吊索橋塔的高度將下降，橋梁整體所受風荷載也變小，對于橋梁抗風都是有益的。

6 結語

綜合分析計算結果，得到結構參數(梁高、梁寬、邊中跨比、垂跨比、支承體系和邊跨輔助橋墩)對公鐵兩用懸索橋的影響規律。前述模型計算出的撓跨比都在1/500左右，所有撓跨比都能滿足條件，表明所給出豎向撓跨比的限值是合理的。所有參數分析時對應的橫向撓跨比，除單跨雙鉸懸索橋有一個特別大的值1/574外，其余模型計算出的撓跨比的值都在1/1 000左右，橫向撓跨比均能滿足給出的建議限值。

整體結構參數對于主梁橫向剛度的影響，在風荷載作用下，改變主梁寬跨比，對橋梁橫向撓度和轉角均影響較大。寬跨比增加，可有效減小橫向撓度和橫向轉角；對于懸索橋垂跨比的減小，風載下主梁橫向撓度和轉角同時減小。3種支承體系中，單跨雙鉸體系懸索橋在抗風中是最不利的。因此，大風地區盡量避免采用單跨雙鉸體系。綜合對比來看，單跨帶伸出跨的懸索橋支承體系是一種比較適宜的選擇。