基于非平穩時間序列分析的發動機訂單預測模型

譚祖健 官丹萍 莫 愁 丁振偉 李曉霞

（1.廣西玉柴機器股份有限公司，廣西 玉林 537005；2.桂林電子科技大學，廣西 桂林 541004）

0 前言

基于已有產品銷售數據預測將來的訂單變化趨勢，進而配備合適的生產所需零部件庫存，并制定合適的生產方案，能夠在很大程度上提高訂單快速交付的能力。對于如何準確地預測產品訂單，眾多研究者均取得過較好成果。杜瑩利用平滑指數模型優化了某汽車公司的訂單預測方法，并改善了該公司生產經營流程中的重復環節，降低了庫存量，提高了效益。佟晶博將動態神經網絡算法引入訂單預測模型中，建立了河蟹電商分銷系統，該系統能夠預測未來一段時間內各分銷商的訂單。李浩等人構建了一種融合VGG 網絡與全卷積網絡（FCN）的出租車多區域訂單預測模型，與基于BP 神經網絡、RBF 神經網絡的預測模型相比，該預測模型平均準確率更高且均方根誤差更低。也有一些研究的目標并非提出成套的預測方法，而是著眼于提升預測過程中某個環節的質量和/或簡便程度。例如DANIEL ORTIZ-ARROYO 等人在模糊邏輯預測模型中，將有序加權平均算子應用于原始時間序列劃分并重構，使一階預測模型精度比對比文獻高，盡管該模型精度仍達不到高階模型的水平，但仍然可以縮短計算時間。劉道元等人為了準確預測某批訂單的剩余完工時間（以便動態調整生產計劃、優化制造過程），提出了一種基于自組織映射（SOM）網絡-特征加權模糊C 均值（FWFCM）的特征選擇算法。在現有的公開文獻中，直接針對發動機訂單預測進行研究的文獻數量較少。

1 模型選擇及模型特性分析

1.1 發動機訂單序列特性分析與模型選擇

根據時間先后順序將一定時間范圍內的采樣數排列成1組或多組數列，這些時間序列可以表征某種特征變量隨著時間不斷變化的過程和趨勢。發動機月訂單數量、季度訂單數量就是一種典型的時間序列。但該時間序列在1 a 周期內的每個月、每個季度都不是固定在某個范圍內的，而是隨著企業產品質量、企業供貨能力、客戶需求以及社會宏觀經濟環境好壞等因素的變化呈一定規律的非平穩變化，而且這個變化是隱含的，需要進一步挖掘才能用一定的模型來表征。由于非平穩時間序列特征數據呈隨機變化的趨勢，其數理統計性質也會隨著時間推移而發生變化，因此對這種特性的數據進行未來趨勢預測時，必須選擇能評估和處理序列中隨機擾動項、能處理數理統計性質變化的模型。滿足這個要求的模型有自回歸條件異方差模型（ARCH 模型（Autoregressive Conditional Heteroskedasticity Model））、灰色模型和自回歸整合滑動平均模型（ARIMA 模型）等。其中，ARIMA 模型在建模時考慮了時間序列的自回歸特性和滑動平均特性，并進行了平穩化處理，因此比較適合分析發動機訂單時間序列和預測未來訂單。

1.2 模型特征分析

自回歸功能可以描述一組變量在前后期的變化特征，即用前期若干時刻的隨機變量的線性組合來表征后期某時段隨機變量的線性回歸。其與用自變量預測因變量的其他線性回歸不同，該功能是用前期的預測后期的（自身）。將該自回歸模型記為（），將隨機序列記為X，其模型結構如公式（1）所示。

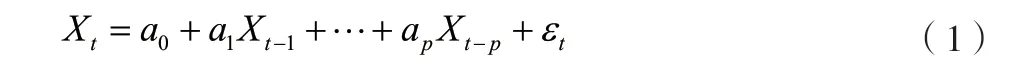
式中：為時間點；為模型階數；，，…，a為自回歸系數（當=0 時，（）去中心化）；{}為白噪聲序列。

對時間點來說，如果有? <，（Xε）=0，即如果任意小于時間點的時間點對應的變量與白噪聲序列相乘，其數學期望均為0，則表明前面的時間序列與后面的白噪聲不相關，這是ARIMA 模型自回歸功能的基本條件和優點。

對發動機訂單時間序列的非平穩性特征來說，線性回歸模型等簡單模型的精度較低。自回歸模型將盡量消除白噪聲影響作為建模目標，因此它可以獲得較高的精度。

對公式（1）來說，只有確定了系數a，其才有使用意義，否則公式（1）就是一個無窮多項式。可以用白噪聲序列ε，ε，ε，…，ε表示隨機序列X，并將滑動平均模型記為MA（），其模型結構如公式（2）所示。

式中：為多項式常數，由變量特征確定；為模型階數；，,…,b為滑動平均系數，且|b|<1，此處=1，2，…，。

如果設定了b的范圍，則公式（2）是收斂的。=1 的特例MA（1）如公式（3）所示。

由公式（3）可知，X為2 個擾動因子（白噪聲）ε和ε的加權平均。根據以上分析可知，MA（）模型是AR（）模型的模型階數受到某種限制時的情形。由于ARIMA 模型融合了AR（）模型和MA（）模型，且值和值的大小體現了這 2 個模型在 ARIMA 模型中作用的強弱，因此在應用時需要確定值和值。

由于類似發動機訂單這樣的時間序列有明顯的趨勢性和/或季節性，因此在建立ARIMA 模型時需要先去除這2 個趨勢，再進行平穩化處理。一般來說，進行1 次差分和2 次差分就可以剔除其中1 個趨勢和2 個趨勢。

1.3 ARIMA建模程序

使用ARIMA 模型進行訂單預測的一般步驟如下：首先，對樣本進行平穩性檢驗，如果不平穩，通常就進行若干次差分，直到樣本平穩。其次，對模型進行定階，確定ARIMA（，，）（為為檢驗樣本平穩性而進行差分的次數）中和值后即可建立模型。再次，對模型進行適應性檢驗，達到誤差要求后才可用于預測未來變量，否則需要重新進行平穩化處理或重新確定階數。ARIMA 建模和預測流程如圖1 所示。

圖1 ARIMA 預測建模流程

平穩性檢驗可以判斷特征樣本隱含的是確定性趨勢還是隨機趨勢（或者二者兼有）。主要方法有以檢驗單位根為手段的笛基-福勒檢驗（Dickey-Fuller 檢驗）和以檢驗誤差項自相關或異方差為手段的菲利普斯-佩隆檢驗（Phillips-Perron 檢驗）。在對模型進行定階時，確定值和值的方法主要有自相關函數法、偏自相關函數法、赤池信息準則（Akaike Information Criterion，AIC 準則）法和貝葉斯信息準則（Bayesian Information Criterion，BIC 準則）法；模型適應性檢檢驗的目的是評估建立的模型時間序列與樣本時間序列的相關性，評價手段是檢驗擬合殘差項{ε}是否為白噪聲。建立的模型建立的模型如果顯著有效，則表現為提取樣本中全部或接近全部相關信息后，殘差沒有相關性，即{ε}應為白噪聲。通常會通過楊-博克斯Q 統計量檢驗（Ljung-Box Q Test，LBQ 檢驗）來評估模型是否顯著有效。

2 實例應用及分析

以某發動機生產商1995—2017 年（共23 a）每季度的發動機訂單為樣本，基于以上理論，使用MATLAB 軟件編制相關程序，建立ARIMA（，，）模型，并預測未來3 a（2018—2020 年）的季度訂單。

2.1 建立一般預測模型

通過Phillips-Perron 檢驗對樣本進行平穩性檢測的方法如下：首先，用最小二乘法估計樣本回歸模型，得到參數估計和殘差序列。其次，利用殘差自相關中的信息計算統計量Z，如果Z滿足設定顯著性水平的限值，則認為該樣本平穩。在MATLAB 中調用pptest 函數進行Phillips-Perron 檢驗的程序語句為[h]=pptest（x,'model','AR'）。其中，（輸入參數）為檢驗的序列，該文為發動機訂單序列；'model','AR'為檢驗的模型選用AR（自回歸）模型；（即輸出參數）為測試結果的布爾決策向量，當=1 時，表示拒絕有單位根的假設，當=0 時，表示不能接受原假設，即模型有單位根。

將實例樣本發動機季度訂單序列作為語句中的量代入，得到=0，則該實例樣本不平穩。因為實例樣本為季度訂單，具有典型的季節性和趨勢性，所以首先，應以=4 的步長做1 次差分去除季節性。其次，以=1 的步長再做1 次差分去除趨勢性。最后，對差分后的時間序列進行同樣的檢驗，檢驗結果表明，該序列平穩。

使用AIC 準則對模型定階的基本原理是針對樣本時間序列建立 ARIMA 模型，用極大似然方法估計模型參數，不同的AR 階數（值）、MA 階數（值）組合會得到不同的殘差、方差的極大似然值，最小極大似然值對應的階次即為最優值、值。在該實例使用AIC 準則時，根據經驗確定最高階次為4，在MATLAB 軟件中運行AIC 準則程序得到的AIC 定階數值分布熱度圖如圖2 所示。圖2 中的數值均為熱度值，深淺不同的顏色表示不同熱度。由圖2 可知，有2 組階數組合的最小極大似然值為1.641，取階數較小者，得到最佳自回歸階數（）=3，滑動平均階數（）=3。

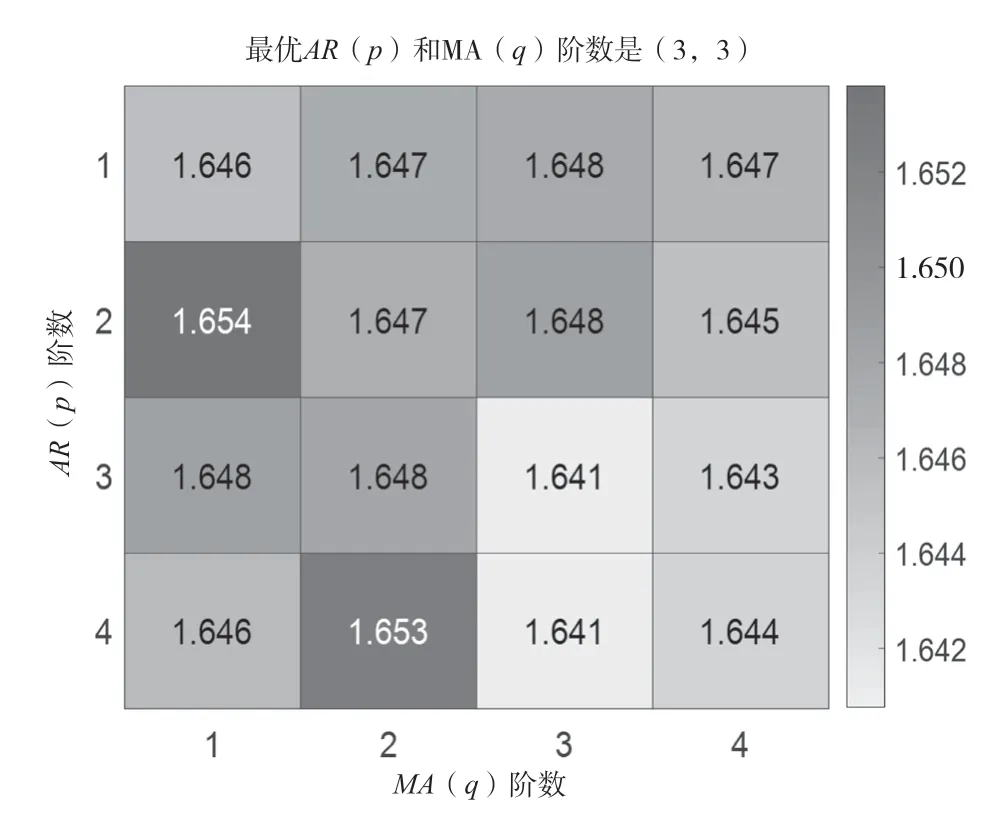
圖2 一般預測模型AIC 定階數值分布熱度圖

根據樣本平穩化處理時所做的差分次數以及使用AIC法則定階時的（）階數、（）階數，可建立模型ARIMA（3，2，3）。然后用LBQ 檢驗來評估模型是否顯著有效。在MATLAB 中調用 lbqtest 函數進行檢驗的程序語句為[h]=lbqtest（reg,'Lags',1:4,'alpha',0.05）。其中，（輸入變量）為用于檢驗的殘差序列；（輸入變量）為檢驗的滯后項數目，這里分別取1、2、3 和4 共4 個項數；（輸入變量）為假設檢驗的顯著性水平，這里取0.05；（輸出變量）為檢驗結果，因為滯后項數目是4，所以這里的測試次數為4 次。在每次得出的結果中，如果=1，則表示拒絕殘差無自相關的零假設，如果=0，則表示不拒絕殘差無自相關的零假設，即說明殘差沒有自相關性。該模型的檢驗結果顯示4 個項數均有=0，可知建立的模型顯著有效。

2.2 未來訂單預測及分析

基于第2.1.3 節建立的模型，可預測2018—2020 年的季度訂單數量。在MATLAB 軟件中調用forecast 函數預測未來訂單的程序語句為[Y,YMSE]=forecast(mdl,12,'Y0',x)。其中，mdl（輸入變量）為建立的ARIMA 模型，即預測的推理依據；12（輸入變量）為預測范圍，即預測未來12 個季度的訂單；'Y0'，意為前樣本響應數據為，即數據初值為發動機訂單序列；（輸出變量）為預測值，為的均值平方誤差。

運行此程序得到的結果如圖3 所示（”預測訂單1“部分）。為了分析預測訂單趨勢和以往實際發動機訂單的變化趨勢，該文將1995—2017 年發動機季度銷量繪制在同一圖中（即圖3“實際訂單”部分）。由圖3 可知，與實際訂單變化情況一樣，2018—2020 年的預測訂單逐年上升，且每年內4 個季度的訂單也逐季上升，呈現明顯的季節性。實際訂單與預測訂單的曲線變化趨勢的一致性較好。

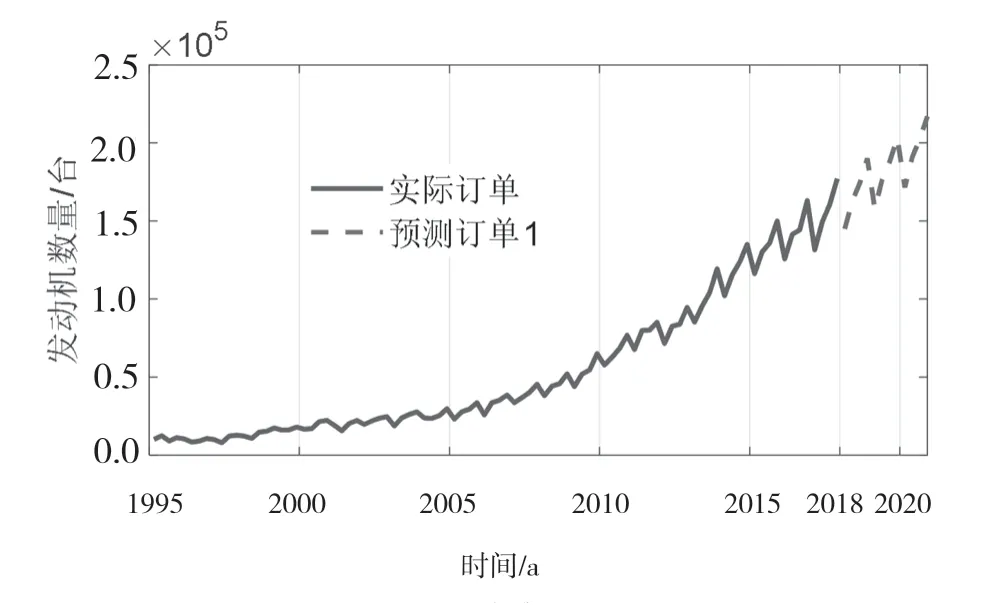
圖3 發動機實際訂單與預測訂單曲線

2.3 季節性預測與一般預測模型建模效果的比較分析

第2.1 節和第2.2 節是根據ARIMA 模型的一般流程來建模并分析的，而文獻[6]給出了一種在MATLAB 中直接利用arima 函數中的“Seasonality”來建立季節性模型的方法。與傳統方法相比，這種方法更簡潔，因為其保留了樣本的季節性，所以建模時只需要進行一次差分去除趨勢性即可。這種建模方法需要配合使用AIC 準則來判斷最優的（）階數和（）階數，方法同第2.1.2 節所述。在MATLAB 中調用ARIMA 函數建立模型的程序語句為model=arima('D',1,'Sea sonality',4,'SARLags',i,'SMALags',j)。

語句含義為根據括號內設置的參數建立一個ARIMA 模型。其中，'D',1 意為差分次數是1；'Seasonality',4 意為季節差分滯后算子多項式程度是4；'SARLags',i,'SMALags',j 意為（）階數和（）階數分別為由AIC 準則確定的最優的值和值。

基于一階差分樣本得到的AIC 定階數值分布熱度如圖4所示。由圖4 可知，各組（）和（）組合對應的極大似然值與樣本經過2 次差分后得到的結果不同，最佳（）=4，（）=1，因此可建立模型ARIMA（4，1，1），并用LBQ 檢驗模型殘差，由檢驗結果可知，該模型顯著有效。用該模型預測的2018—2020 年季度訂單數量如圖5 所示（“預測訂單 2”部分）。

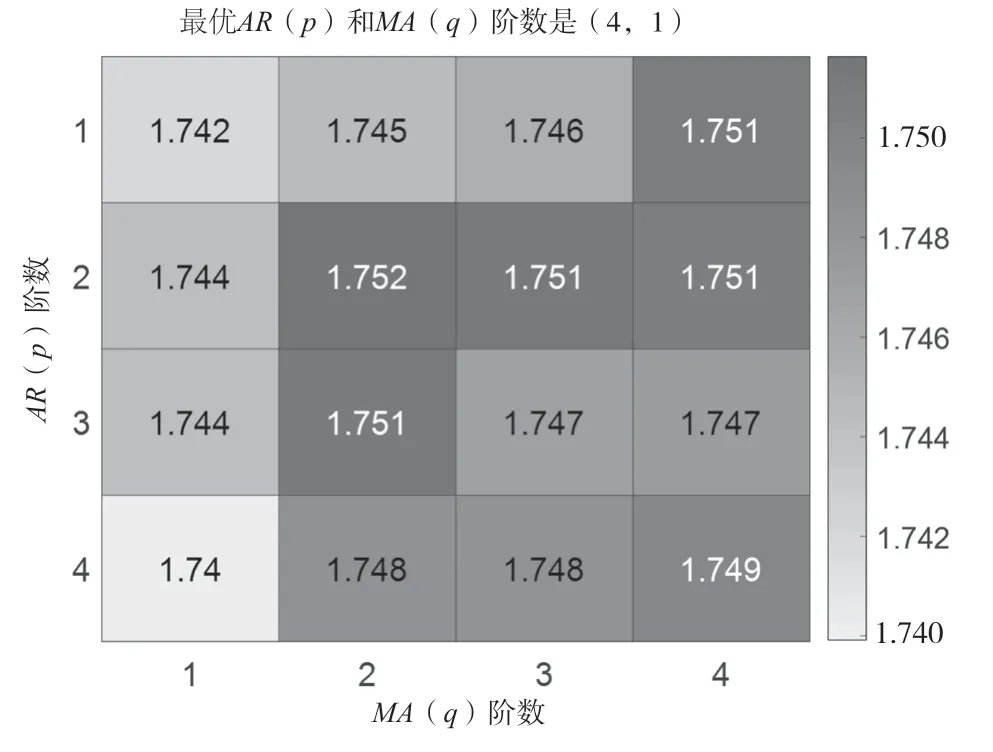
圖4 季節性預測模型AIC 定階數值分布熱度圖

為分析模型可信度，該文將2018—2020 年實際的發動機季度訂單與2 種建模方法所得的預測訂單進行比較，繪制的變化曲線圖如圖5 所示。由圖5 可知，2 種方法所得的預測訂單都很好地跟隨了實際訂單的變化，且除2020 年第一季度外，季節性預測模型所得預測訂單均更接近實際訂單的變化。2 種方法所得的2020 年第一季度預測訂單與實際訂單的相對誤差分別為6.2%和9.3%，而其他季度的相對誤差均為0.9%～2.3%，誤差較小。整體分析預測值與實際值的相關性，在顯著性水平=0.05 的情況下，2 種模型的預測結果均有決定系數=0.89，在滿意范圍內。

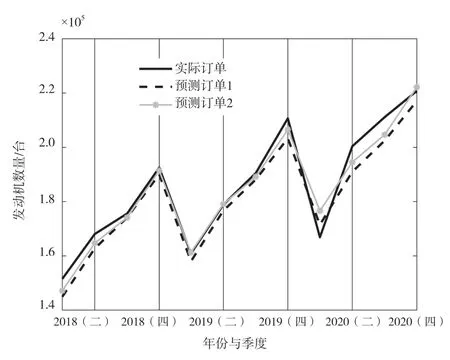
圖5 2018—2020 年預測訂單與實際訂單的比較

時間序列預測基于這樣一個假設：預測期與樣本采樣期的環境條件基本相同。而2020 年第一季度由于受新冠疫情影響，國內外生產經營環境嚴重惡化，樣本采樣公司當季銷量同比增幅極小，而當季的預測值與實際值較大誤差為9.3%。

3 結論

為了滿足快速交付訂單的客戶需求，首先，該文研究了某公司1995—2017 年（共23 a）的發動機銷量時間特性，選擇ARIMA 模型建立發動機訂單預測模型。其次，分析了ARIMA模型適用于非平穩時間序列分析的自回歸功能、滑動平均功能和平穩化處理特征，給出了訂單預測模型的建模步驟。再次，以某公司以往訂單為訓練樣本，使用該模型預測了2018—2020 年3 a 的季度訂單，結果表明，預測訂單的變化曲線與以往實際銷售數量的變化曲線的一致性較好。從次，將2018—2020 年的預測訂單與實際訂單進行比較，結果顯示兩者誤差較小，決定系數較高。最后，得出該文所建立的預測模型具有較高的可信度，可以對發動機訂單進行預測。