基于改進樽海鞘群和最小二乘支持向量機算法的新型彈藥質量評估方法

楊建新， 蘭小平， 馮亞東， 楊一銘， 郭志明

(1.中國兵器工業信息中心， 北京 100089； 2.中國兵器科學研究院， 北京 100089)

0 引言

彈藥產品通常采用批次化連續生產方式，在交付部隊前必須進行質量一致性檢驗，判斷產品質量在生產過程中是否穩定，是否符合制造與驗收規范的要求。由于彈藥產品屬于一次性消耗品，在靶場試驗時無法進行大樣本試射試驗。因此，根據已有試驗數據進行建模研究，在不增加試驗次數情況下通過研究彈藥產品的質量狀態，對彈藥批次質量進行評估，代替部分靶場試驗，是一種減少試驗次數、降低試驗消耗的有效途徑。

目前，彈藥質量評估已引起學者們的廣泛關注和研究。曹柬等提出了一種基于層次分析法和三角模糊數理論的模型，通過充分綜合專家組評估意見實現導彈系統性能的定量分析。吳曉云等借助粗集約簡和屬性重要性理論，建立了層次分析模型與粗集決策表間的聯系，實現了層次分析法對領域知識的充分利用及粗集對層次結構問題的決策支持，并將該方法用于某火箭炮武器系統改進方案的綜合評估中。張永久等通過研究不同參數對導彈質量性能的影響方式和程度，利用層次分析法結合專家征詢法建立質量指標體系和權重，實現對全彈質量綜合評判。李俊等采用粗糙集理論結合相關機器學習的方法，以導彈武器在壽命周期中的質量數據為基礎，從中自動分析、提取導彈武器的質量性能評估規則，在一定程度上實現了對武器質量狀況評估的客觀性；安進等在綜合考慮導彈質量評估流程的基礎上，運用模糊綜合評判法和組合賦權法，構建了基于關鍵控制點的質量評估模型，理論上能夠較客觀地對大型復雜產品質量進行綜合評估。黃睿等基于導彈質量數據信息，運用系統工程理論及分析方法設計了某型導彈性能質量評估系統，實現了對該型導彈性能質量的準確評估與預測。周璐等采用層次分析法對導彈的質量評定體系進行分類，構建導彈質量評估框架，對導彈各系統以及整體進行了質量綜合評定。上述研究存在以下不足：1)彈藥質量評估模型是通過層次分析、模糊評判、系統工程等理論并結合專家征詢打分的方法進行構建，質量評估結果難以克服主觀因素的影響，準確性和置信度不足；2)評估過程沒有充分利用彈藥制造過程的質量數據，難以給出客觀、準確的彈藥質量評估結果。

近年來，數據挖掘、機器學習等技術的興起為復雜產品質量管理提供了新的選擇。董海等對車身制造工藝過程數據進行實時采集與數據挖掘處理，建立車身尺寸裝配質量評估模型，實現了車身裝配質量的準確快速地預測。羅陽等利用基于貝葉斯估計的推力預測模型與基于高斯過程的類空化誤差補償，實現了水下螺旋槳推進器的推力預測。于勇等提出基于機器學習算法的質量預測與工藝參數優化方法，利用多種機器學習分類器構建基于工藝參數與質量分類標簽的質量預測模型，實現了機加零件的質量預測和工藝參數優化。顏永龍等通過建立基于反向傳播神經網絡和最小二乘支持向量機(LSSVM)的組合預測模型，并引入信息熵對殘差數據進行處理，實現了對風電機組質量狀態的在線預測。然而，利用數據挖掘、機器學習等技術進行彈藥質量評估的研究工作尚處于探索階段，目前的文獻中還未涉及基于彈藥實測數據進行彈藥質量評估的相關研究。

彈藥產品由于造價昂貴、危險性高，不可能做大量的現場試驗進行質量評估，這就涉及到小子樣情況下裝備的質量評估問題。貝葉斯(Bayes)方法作為一種研究小子樣問題的有效方法，可充分利用先驗知識彌補現有樣本量的不足，在確保產品質量的前提下有效地減少現場試驗量。LSSVM作為SVM的改進算法，通過引入最小二乘損失函數和等式化約束的方法，將最優化問題的求解轉化為求解線性方程，針對小樣本數據進行回歸預測時兼具全局最優和有較好的泛化性能的優點。基于此，本文將Bayes理論、樽海鞘群算法(SSA)以及LSSVM相結合，提出了一種基于Bayes-基于精英質心反向學習改進的樽海鞘群算法(ECOSSA)-LSSVM的新型彈藥產品質量評估方法。首先，以新型彈藥靶場試驗樣本數據為基礎，利用Bayes理論對當前批次彈藥發射成功率進行估計；其次，確定影響新型彈藥質量的關鍵質量特性，收集其制造過程的相關質量數據，對關鍵質量特性過程能力指數進行計算；然后，引入精英質心和反向學習策略對傳統SSA算法進行改進，并使用改進后的SSA算法對LSSVM中懲罰因子及核函數參數進行優化；最后，以彈藥制造過程關鍵質量特性過程能力指數為輸入、批次彈藥發射成功率為輸出，使用優化后的LSSVM算法完成新型彈藥質量評估模型的構建，并以某新型彈藥為例進行應用分析，驗證該方法的可行性和有效性。

1 相關理論

1.1 新型彈藥發射成功率估計

根據質量的定義，彈藥質量就是其能完成作戰目標的程度，在靶場試驗中表現為彈藥能否正常發射、飛行并精確打擊目標點。若彈藥發射成功，則飛行成功，落點偏差滿足設計要求，稱為成功，記為1；若彈藥發射失敗，則飛行失敗，落點偏差不合格，稱為失敗，記為0。假定某新型彈藥的試驗成功率為，進行次靶場試驗后獲得試驗樣本的子樣,,…,(為試驗樣本總量)，由于在靶場試驗中只有成功和失敗兩種結果，通常采用貝塔分布(,)作為Bayes估計時的先驗概率密度，其密度函數為

(1)

式中：和為先驗概率密度的超參數。

根據Bayes理論，得到后驗概率密度函數：

(2)

式中：為抽樣試驗成功的次數。

該分布是以(+,+-)為參數的貝塔分布，由共軛先驗分布可知的后驗分布仍然是貝塔分布(+,+-)。常用的Bayes點估計是后驗期望估計，對于貝塔分布(,)數學期望為

(3)

對于后驗分布貝塔分布(+,+-)，可知的Bayes估計為

(4)

先驗概率密度中超參數和需要用收集的先驗信息加以確定，新型彈藥由于缺乏歷史試驗數據，可以認為其先驗概率在[0，1]區間為均勻分布，此時==1，新型彈藥發射成功率的Bayes估計為

(5)

1.2 過程能力指數

彈藥生產過程一般包含原材料投料、機械加工、表面處理、裝配調試等業務環節，每個環節都會累積大量質量數據，這些數據通常反映了彈藥產品質量水平。在彈藥產品生產條件、工藝水平、原材料供應基本穩定的前提下，制造過程質量的穩定性直接影響彈藥最終質量狀態。

過程能力指數是指工序在一定時間內處于控制狀態下的實際加工能力，是衡量產品質量和性能的有效手段。彈藥產品通常采用連續批生產方式，處在統計控制狀態時其質量特性會出現正常波動，所處幅度是彈藥加工過程能力。過程能力指數主要有以下3種形式：過程能力指數，單側規范值的過程能力指數和。

1)對于雙側公差情況，過程能力指數的計算公式為

(6)

式中：表示質量特性的上限；表示質量特性的下限；為質量特性的方差。

2)對于單側公差情況，質量特性只做下限值的要求時，過程能力指數記為：

(7)

式中：表示總體均值。

3)對于單側公差情況，質量特性只做上限值的要求時，過程能力指數記為：

(8)

2 基于ECOSSA和LSSVM的新型彈藥質量評估模型

2.1 LSSVM

LSSVM是在標準SVM上的一種改進，通過將不等式約束轉換成等式約束，并以最小二乘線性系統取代二次規劃作為損失函數，具有全局最優、適應性強等優點。對于給定訓練樣本數據集{(,)，(,)，…，(,)，…，(,)}，,∈，其中為輸入變量，為期望值，使用非線性映射(·)將樣本輸入從原空間映射到高維特征空間，則LSSVM的回歸函數表示為

()=()+

(9)

式中：()為核空間映射函數；為權向量；為偏置參量。

依據結構風險最小化原則，LSSVM求解二次規劃問題可描述為

(10)

式中：為引入的松弛因子組成的向量；為第個松弛變量；為正則化常數。

引入拉格朗日乘子向量，則構造拉格朗日函數為

(11)

最優解的條件為

(12)

將(12)式轉化為求解線性方程組，即

(13)

式中：(,)為核函數，(,)=()()。

求解該線性方程組，即可得到LSSVM回歸估計為

(14)

本文中核函數采用機器學習中常用的徑向基函數(RBF)，RBF將輸入樣本點映射成新的特征向量，然后得到該特征向量的點乘。因此，RBF的本質是將每一個樣本點映射到一個無窮維特征空間，其表達式為

(,)=exp (-‖-‖)

(15)

對選用徑向核函數的LSSVM而言，正則參數和核函數參數的合理選擇直接影響最終模型的復雜度和精確度，因此正則系數和核函數參數十分重要。

2.2 改進的SSA

SSA作為一種新型元啟發式智能算法，算法結構簡單，利用“鏈”結構模式可有效避免傳統“群”結構模式(如粒子群優化、蟻群、灰狼群等)中因領導者前期搜索不充分而陷入局部極值情況的發生，并且該算法能夠有效尋找全局最優解，己成功應用于機械設備故障診斷、短期風機功率預測等問題的求解中。樽海鞘群體分為兩類：領導者和跟隨者，領導者位于樽海鞘鏈的最前面，負責探索食物的位置；其他個體則為追隨者，逐個相連。SSA定義每個樽海鞘個體的位置矢量用于維空間中搜索，為決策變量的數目。因此種群向量由×維矩陣構成，即

(16)

領導者以食物源為目標，不斷更新自身位置，因此食物源的位置是所有樽海鞘個體的目標位置，領導者的位置更新公式為

(17)

=2e-(4)

(18)

式中：為當前迭代次數；為最大迭代次數。

追隨者的位置更新可表示為

(19)

傳統SSA中，領導者的位置只受食物源位置的引導，當迭代后期搜尋到局部最優解時，當前策略很難有效地跳出局部最優，從而影響算法的速度及精度。為進一步提高基本SSA算法的求解精度和收斂速度，本文提出一種ECOSSA。該算法首先引入精英質心概念，使領導者的位置更新不再僅受食物影響，還能有效利用精英個體的有效信息，將領導者向群體中的精英個體牽引，然后利用反向學習策略在精英個體所構成的定義區間內產生反向解，引導搜索過程向全局最優解逼近，有效避免算法陷入局部最優，提高算法全局搜索性能及收斂速度。

精英質心。設(,,…,)是選取的樽海鞘群體中的個精英個體，每個個體都有維，精英質心的定義為

(20)

將群體中精英個體的位置信息加入領導者的位置更新過程，使領導者的位置更新不再只受上一代食物位置的牽引，還受到群體中精英個體的影響，充分利用精英個體的有效信息提高算法的探索能力，改進后領導者更新公式為

(21)

(22)

式中：為介于0和1之間的隨機數。

(23)

樽海鞘領導者在當前解空間和反向解空間中同時進行搜索，選擇兩個空間中最優解作為下一代領導者的位置，這樣算法更容易跳出局部最優解，提高算法的全局搜索性能。

改進后領導者位置更新公式如下：

(24)

式中：_和_分別表示領導者在第維上的當前解和反向解。

2.3 新型彈藥質量評估模型構建

基于LSSVM構建的新型彈藥質量評估模型預測精度與正則系數和核函數參數的選擇密切相關，如果和選擇不合理，將導致預測結果的精度低、可靠性不高。本文將ECOSSA用于LSSVM參數的尋優，適應度函數為預測的平均絕對誤差(MSE)，

(25)

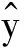
新型彈藥質量評估模型構建流程如圖1所示。

圖1中，，…，代表某個關鍵質量特性對應的過程能力指數向量，代表預測值向量。模型具體構建步驟如下：

在質量受控狀態下，對新型彈藥制造過程的質量數據進行采集，作為輸入樣本數據。

將上述新型彈藥產品分組進行靶場試驗，根據靶場試驗數據，利用Bayes理論對當前批次彈藥發射成功率進行估計，作為輸出樣本。

將樣本數據進行預處理，并分為訓練集和測試集。

初始化ECOSSA的各項參數。設定種群規模、最大迭代次數、精英個數及搜索空間[，]。

在搜索空間內隨機產生種群個體的位置。

將群體位置信息分別代入LSSVM，根據(25)式計算均方誤差MSE。

圖1 新型彈藥質量評估流程Fig.1 Quality evaluation processes of new ammunition

以均方誤差MSE作為樽海鞘的適應度值，將適應度最好的樽海鞘位置作為食物位置。

確定食物位置后，根據(24)式及(19)式更新領導者及跟隨者的位置。

計算更新后樽海鞘個體的適應度值，并與當前食物的適應度值進行比較，若更新后的樽海鞘適應度值優于食物，則將該樽海鞘的位置定義為新食物位置。

重復步驟6～步驟9，直到滿足算法終止條件，輸出最優適應度值和最優值所對應的LSSVM參數組合(，)。

將測試數據輸入新型彈藥質量評估模型模，對模型精準度進行驗證。

3 案例分析

3.1 試驗數據準備

某新型彈藥型號研制完成后，對收集到的歷次靶場試驗數據進行統計分析，得到各批次新型彈藥發射成功率的Bayes估計，如表1所示。

表1 新型彈藥發射成功率貝葉斯估計Tab.1 Firing success rateofnew ammunition based onBayesian estimation

由于新型彈藥制造過程中影響因素眾多，質量特性數據的合理選擇尤為重要。若選取的質量特性數據不同，則LSSVM方法中回歸映射的權向量也會不同，必然會影響所構建模型的評估結果。為保持一定的模型精度，需要選取最具代表性的質量特性數據來真實反映新型彈藥的評估建模過程，然而通過人工經驗進行特征數據選擇會引入主觀判別因素，影響模型評估精度。本文采用基于失效模式分析方法對彈藥制造過程質量影響因素及其關鍵部件制造過程質量控制要素進行識別，提取影響彈藥產品質量的關鍵質量特性。經過失效樹分析，影響該型彈藥的關鍵質量特性參數為10個，其中、、分別為零件1、零件2、零件3在加工階段的關鍵質量特性，、、、分別為部件4、部件5、部件6、部件7在裝配階段的關鍵質量特性，、、分別為部件8、部件9、部件10在整彈總裝總調階段的關鍵質量特性。

將樣本數據中前35個批次數據作為訓練樣本，后15個批次數據作為測試樣本，分別計算各個批次產品關鍵質量特性的過程能力指數。通過查閱圖紙，～均為雙側公差，故用(6)式計算其過程能力指數，數據如表2和表3所示。

3.2 仿真實驗與結果分析

以MATLAB R2018軟件為仿真實驗平臺，利用表2中新型彈藥樣本數據訓練基于ECOSSA和LSSVM的新型彈藥質量評估模型，并將評估模型得到的輸出結果與真實值進行對比，如圖2所示。從圖2中可知，評估模型輸出的預測值與真實值相近，表明評估模型對訓練樣本具有良好的擬合效果。

表2 訓練樣本集Tab.2 Training sample set

表3 測試樣本集Tab.3 Test sample set

圖2 訓練樣本預測值與真實值對比Fig.2 Comparison chart of predicted value and true value of training sample

為了進一步對ECOSSA-LSSVM模型的有效性進行驗證，本文選取LSSVM、基于SSA優化的LSSVM(SSA-LSSVM)、基于PSO算法優化的LSSVM(PSO-LSSVM)分別建立新型彈藥質量評估模型，利用表3中的測試數據對4種模型的預測效果進行對比，對比結果如表4所示。結果顯示，LSSVM模型誤差最大，平均誤差為3.17%，PSO-LSSVM與SSA-LSSVM平均誤差為2.28%和2.24%，本文設計的ECOSSA-LSSVM模型平均誤差最小，控制在2%以內。

圖3給出了各模型對測試樣本真值的預測情況。從圖3中可以看出，各模型的預測值都不同程度地接近真實值，其中ECOSSA-LSSVM模型對樣本的預測值與真實值近似度最高，表明本文設計的模型預測準確度高于對比組。

圖4和圖5所示為各模型預測結果的絕對誤差及相對誤差曲線圖。從圖4和圖5中可以看出：傳統的LSSVM模型誤差最大，最大誤差達到±5%；PSO-LSSVM與SSA-LSSVM模型的相對誤差在±4%之間波動；本文設計的ECOSSA-LSSVM模型誤差最小，控制在2%以內，且誤差的波動范圍比其他模型較小，表明本文設計的評估模型具有較好的泛化性與較強的魯棒性。

為更加科學、合理地驗證所設計模型的穩定性，對各模型預測結果的均方誤差進行計算，結果如圖6所示。由圖6可以看出，未經優化的LSSVM模型誤差波動范圍最大，均方誤差為9.2×10；PSO算法和SSA算法優化后的LSSVM模型穩定性略好于傳統LSSVM模型，均方誤差約為5.1×10；ECOSSA算法優化的LSSVM模型預測結果的均方誤差大大減小，僅為0.7×10，證明本文設計的評估模型的精度和穩定性更高，算法能夠更好地找到全局最優解。

表4 算法預測結果對比Tab.4 Comparison of predicted results

圖3 測試樣本預測值與真實值對比Fig.3 Comparison chart of predicted value and true value of test sample

圖4 絕對誤差對比Fig.4 Comparison chart of absolute error values

圖5 相對誤差對比Fig.5 Comparison chart of relative errors

圖6 均方誤差對比圖Fig.6 Comparison chart of mean square error

此外，為驗證本文ECOSSA的運行速度，將PSO算法、SSA及ECOSSA分別在10維和30維的CEC2017測試函數上進行計算，獨立運行10次并統計其平均運行時間，結果如圖7所示。由圖7可以看出：PSO算法、SSA及ECOSSA在10維函數上的平均運行時間分別為1.15 s、1.08 s和0.92 s，在30維函數上的平均運行時間分別為5.02 s、4.69 s和4.03 s；兩組實驗中ECOSSA算法的平均耗時均少于PSO算法和SSA，其中改進后的SSA運行時間與標準SSA對比，運行速度提升了15%左右，這歸功于通過引入精英質心和反向學習機制，ECOSSA在尋優過程中能夠更快地跳出局部最優，從而減少了算法運行時間。

圖7 運行時間對比圖Fig.7 Running time

4 結論

本文針對新型彈藥質量評估中樣本數量少、試驗消耗大、未有效利用制造過程質量數據等問題，提出一種基于ECOSSA和LSSVM的新型彈藥質量評估方法，通過建立彈藥制造過程中關鍵質量特性過程能力指數與彈藥發射成功率之間的關系，實現了基于彈藥制造過程質量數據對彈藥發射成功率的量化評估。得出主要結論如下：

1)引入精英質心的概念對SSA進行改進，能使領導者的位置更新有效利用上一代精英個體的有效信息，在此基礎上構造精英個體的反向解空間，引導搜索過程向全局最優解逼近，有效避免陷入局部最優解，提高算法全局搜索性能及收斂速度。

2)通過選取某新型彈藥產品相關樣本數據對本文設計的ECOSSA-LSSVM模型進行有效性驗證，并與LSSVM、PSO-LSSVM、SSA-LSSVM 3種模型進行對比分析。實驗結果顯示，ECOSSA-LSSVM模型將評估的平均誤差控制在2%以內，算法運行時間與標準SSA算法對比，運行速度提升了15%左右。證明了本文提出的新型彈藥質量評估模型可有效解決彈藥產品小子樣質量預測誤差大的問題，在實踐中具有很大的應用潛能。

3)對于不同類型的彈藥產品，采用本文方法進行彈藥質量評估模型構建時，選取的關鍵質量特性可能不同，但是評估模型構建過程和計算方法一致；與此同時，對于已經積累了大量靶試數據的非新型彈藥產品，靶試成功率的先驗概率可以由歷史試驗數據統計獲得，Bayes估計結果將更準確，由此訓練的評估模型和彈藥質量評估結果也將更趨向于實際。