混合動力履帶車輛機電聯合制動控制

張偉， 劉輝， 韓立金， 劉寶帥， 張勛， 張萬年

(北京理工大學 機械與車輛學院， 北京 100081)

0 引言

制動性能是體現履帶車輛機動性的重要指標，隨著履帶車輛向高速化、重載化和智能化方向發展，混合動力與純電驅動等新能源車輛技術逐步應用于履帶車輛領域。引入電驅動技術的履帶車輛采用機電式聯合制動系統，與傳統履帶車輛機械式和機- 液混合式[1]制動系統相比，機電聯合制動系統不僅能夠回收制動能量、提高能源利用率，而且能顯著減小機械制動器的磨損與熱負荷，從而延長使用壽命[2-3]，同時該制動方式控制靈活、響應快，對改善制動過程中普遍存在的履帶滑移現象、提升履帶車輛的制動性和行駛安全性具有較大應用潛力，特別是在泥濘、冰雪等路面上制動出現的履帶打滑、主動輪抱死等失穩工況具有顯著優勢[4-6]。

機電聯合制動系統能夠滿足高速、頻繁、長時間和大制動力需求，相關研究對于行駛環境惡劣的履帶車輛具有重要意義。目前，針對民用輪式車輛的機電聯合制動研究較多，已研發出豐富的理論成果和應用技術[7-12]，但是針對履帶車輛研究較少，主要集中在機電聯合制動力矩分配控制策略方面。周秋君等[13]針對電傳動履帶車輛制動過程，分析了高、中、低速條件下電氣制動、機械制動和機電聯合制動的特性，提出理想三段式制動控制策略，改善了制動器的溫升，延長了制動器的壽命。馬田等[14]研究發現理想三段式聯合制動策略存在制動時間過長的問題，摒棄高速純電氣制動的策略，提出改進的兩段式機電聯合制動控制策略。李峰等[3]針對三段式機電聯合制動控制策略的不足，基于模糊控制思想，提出基于車速、踏板行程和電池荷電狀態(SOC)等因素的機電聯合制動力分配模糊控制策略，該策略具有更好的制動效能，但未考慮電機制動力矩的飽和因素，存在動態協調失準隱患。曾慶含等[15]充分考慮電機制動能力約束，基于駕駛員意圖識別，改進了模糊控制策略。但該策略以電氣制動分配系數為參考值，以機械制動力補償電氣制動，存在響應時間不匹配問題，動態波動較大。張曉辰等[16]同樣采用模糊控制策略，為解決傳統門限控制策略中門限參數漂移適應能力差、模式切換頻繁、能量回收率低等問題，采用粒子群優化算法對模糊隸屬度函數進行了優化。生輝等[17-19]針對高速電驅動履帶車輛，分析了機械制動器、電機和電液緩速器3種制動系統制動轉矩的動態特性，提出前饋- 反饋動態協調控制算法，解決了擾動情況下多系統聯合制動的力矩波動問題。此外，陳朝萌等[4]、張舒陽[5]等、Zhang等[6]關注履帶車輛的制動穩定性，分析履帶滑移問題，研究了在履帶- 地面附著極限條件下的機電聯合制動控制策略，有效減少了主動輪抱死和履帶過大滑移現象。

以上研究主要針對雙側電驅動履帶車輛，對于雙模混聯式混合動力履帶車輛機電聯合制動的研究尚未涉及。本文以裝配機電復合傳動(EMT)系統的某型重載混合動力履帶車輛為對象，進行機電聯合制動智能控制理論研究，充分考慮地面附著條件、運行工況、電機狀態等約束條件，兼顧制動安全性、制動穩定性、能量回收效率以及路況適應性等控制目標，設計了一種以電機制動能力飽和度為控制目標的全工況機電聯合制動控制策略，并進行了仿真驗證。

1 系統模型

1.1 雙模混聯混合動力履帶車輛系統構型

雙電機混聯式混合動力履帶車輛的傳動系統結構[20]如圖1所示。該型混合動力履帶車輛傳動系統由發動機、電池組、雙驅動電機、前傳動、離合器、制動器、行星齒輪組機構等組成。圖1中，CL為離合器，BK表示制動器，k1、k2、k3為行星輪系參數。車輛參數如表1所示。

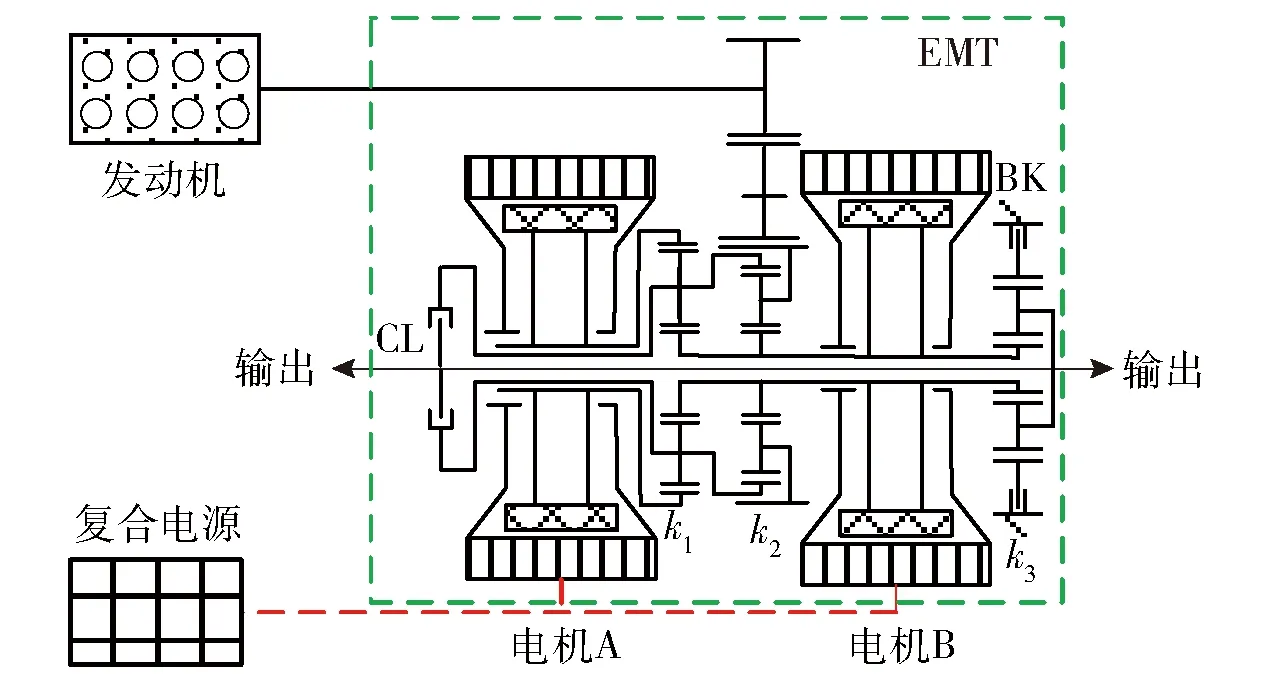
圖1 前傳動及耦合機構系統結構Fig.1 Structure of front transmission and coupling mechanism

通過離合器和制動器的狀態切換組合，可以實現多種驅動模式，其中混合驅動模式有兩種，分別為電動無極變速1(EVT1)模式和電動無極變速2(EVT2)模式。混合驅動模式下發動機、電機、離合器狀態如表2所示。

表1 雙模混聯混合動力履帶車輛基本參數Tab.1 Basic parameters of dual-mode hybrid tracked vehicle

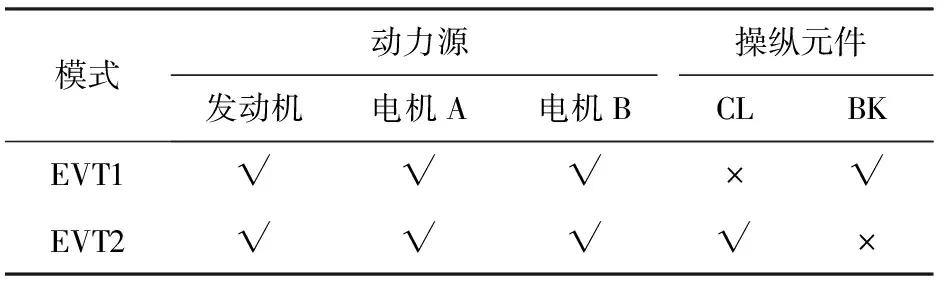
表2 混動模式下部件狀態Tab.2 Component status in hybrid mode

1.2 整車縱向動力學模型

履帶車輛制動過程受力如圖2所示。圖2中，v為車速，Fw為空氣阻力，Ff為滾動阻力，Fb為制動阻力，Fp為坡道阻力，Fn為履帶接地面法向力，α為坡度角，G為整車重力，其中G=mg，g為重力加速度。

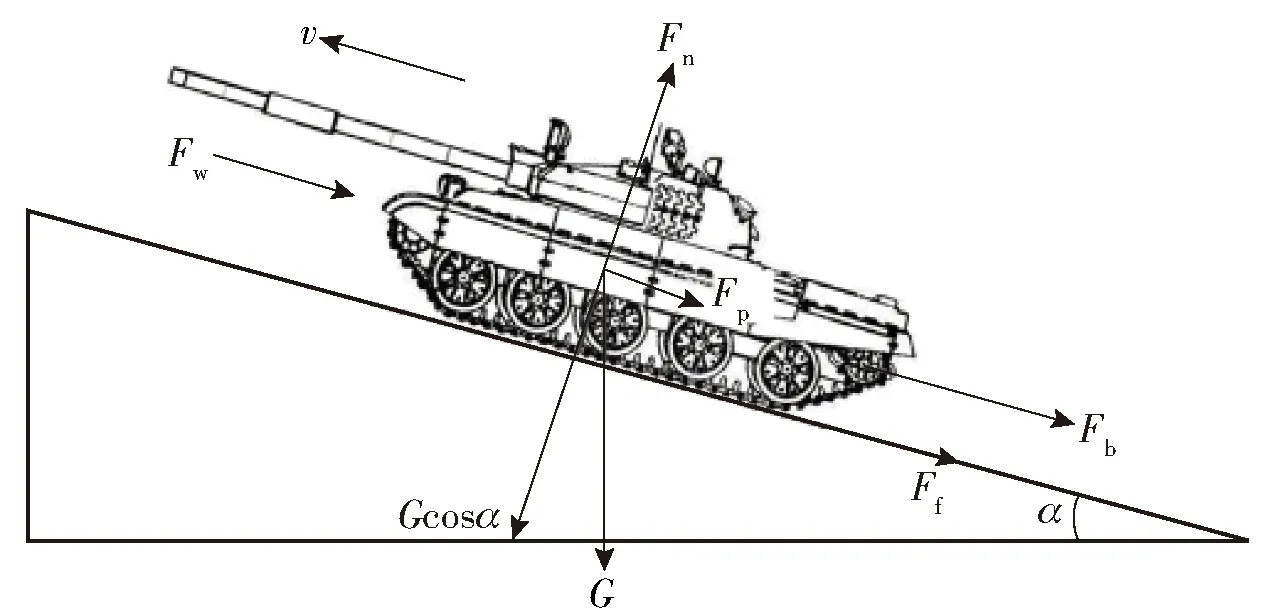
圖2 履帶車輛縱向受力分析Fig.2 Longitudinal force analysis of tracked vehicle

因此有

(1)

式中：Ω為旋轉質量轉換系數；

(2)

f為滾動阻力系數，由試驗測定，A為履帶車輛正投影面積，CD為空氣阻力系數。

1.3 行走系統動力學模型

假設制動過程中履帶是柔軟的不可拉伸的帶，且履帶上的所有的點都處于同一個平面內，如圖3所示。圖3中，Tb為主動輪制動力矩。

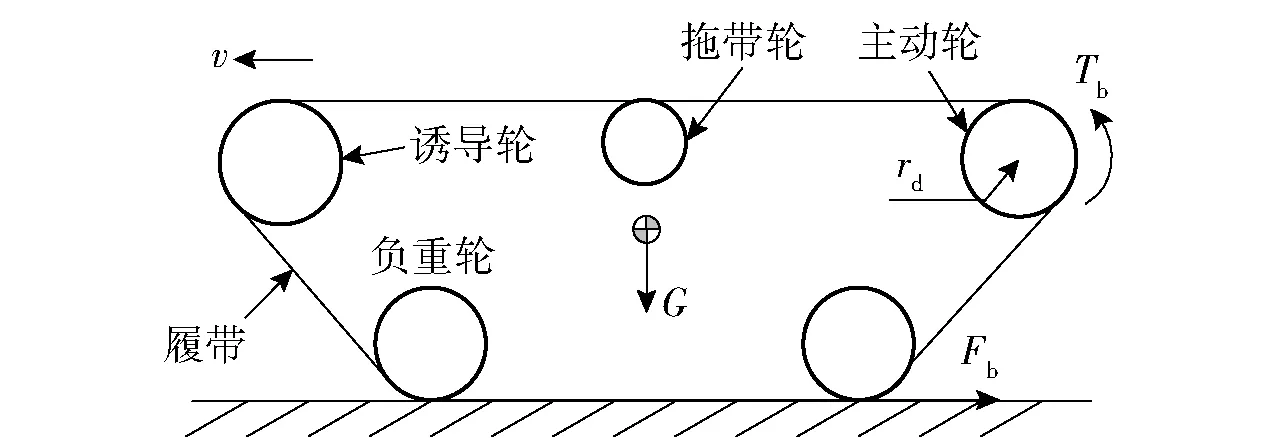
圖3 制動過程履帶受力分析圖Fig.3 Track force diagram during braking

地面制動力可簡化為履帶與主動輪之間的相互作用力，則履帶車輛制動動力學模型為

(3)

式中：ωd為主動輪轉速。若地面不打滑，則有v=rdωd。

聯立(1)式～(3)式，可得

(4)

地面施加的制動力Fb并不能夠無限增大，其上限主要是土壤抗剪切強度決定的。Fb的最大值與履帶接地面法向力Fn的比值為地面附著系數μ，即

Fb≤μ·Fn

(5)

根據履帶- 土壤接觸動力學模型[5]，有

μ=(1-λ)μΔ+μv

(6)

式中：λ為履帶滑動實際滑移率，λ=0時履帶純滾動，λ=1時履帶抱死拖滑；μΔ為履帶與地面間靜摩擦系數，其最大值為μs，對應門限變形量為Δmax；μv為履帶與地面動摩擦系數，其最大值和最大靜摩擦系數相等，即μv_max=μs，對應相對速度us，在履帶抱死拖滑時值為μd，對應相對門限速度為ud。其中，各參量表達式為

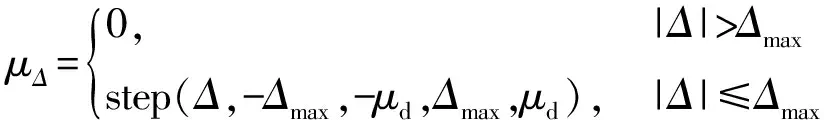
(7)

ur為履帶接地段相對地面速度。當ur=us時路面附著系數μ有最大值。典型地面附著系數試驗數[4]如圖4所示，可見μ峰值區間位于λ值25%～30%區間。

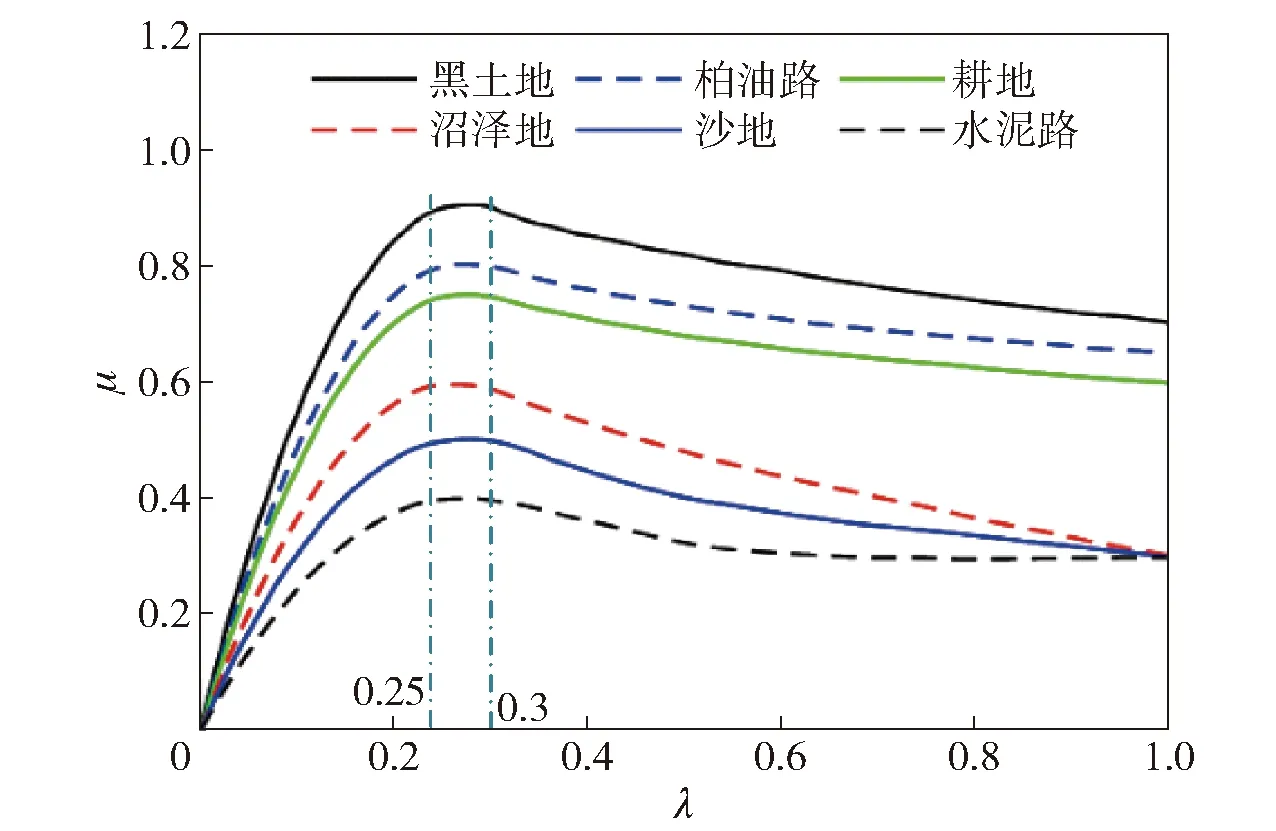
圖4 履帶車輛典型地面附著系數- 滑移率曲線Fig.4 Common ground adhesion coefficient-slip ratio curve

1.4 驅動系統模型

機械制動力矩控制器及液壓系統動態響應模型可以近似為1階慣性系統：

(8)

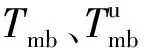
發動機及其控制器可簡化為轉矩響應傳遞函數模型[20]為

(9)

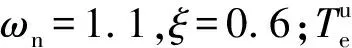
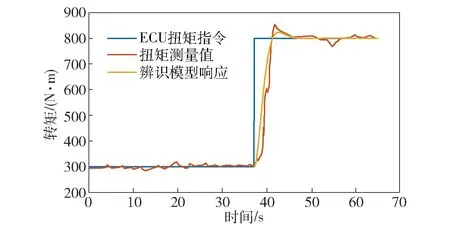
圖5 發動機轉矩模型辨識試驗(ωe=2 400 r/min)Fig.5 Engine torque model identification test(ωe=2 400 r/min)

面向控制的永磁同步電機模型可簡化為1階傳遞函數[21]。電機動態響應轉矩為

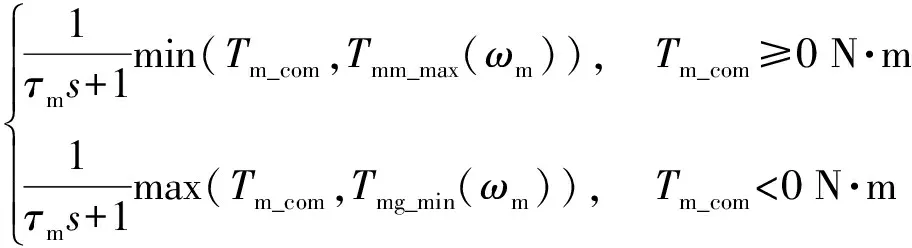
(10)

式中：τm為轉矩響應時間常數；Tm_com為目標轉矩；Tmm_max為驅動工況最大轉矩；Tmg_min為發電工況最大轉矩；ωm為電機轉速。

1.5 傳動系統模型

動力耦合及變速機構由多個行星排、離合器、前傳動、側傳動等組成，是2自由度慣性耦合系統。設行星機構的特性參數為k1、k2，根據圖1中行星輪系的連接關系，EVT1和EVT2模式穩態工況下耦合機構靜態模型可分別由(11)式和(12)式描述：

(11)

(12)

式中：ωA、ωB、ωi、ωo分別為電機A、電機B、輸入軸和輸出軸轉速；TA、TB、Ti、To分別為電機A、電機B、輸入軸和輸出軸轉矩。

由行星輪系運動傳遞關系，可得EVT1和EVT2模式下的系統動態模型分別為(13)式和(14)式：

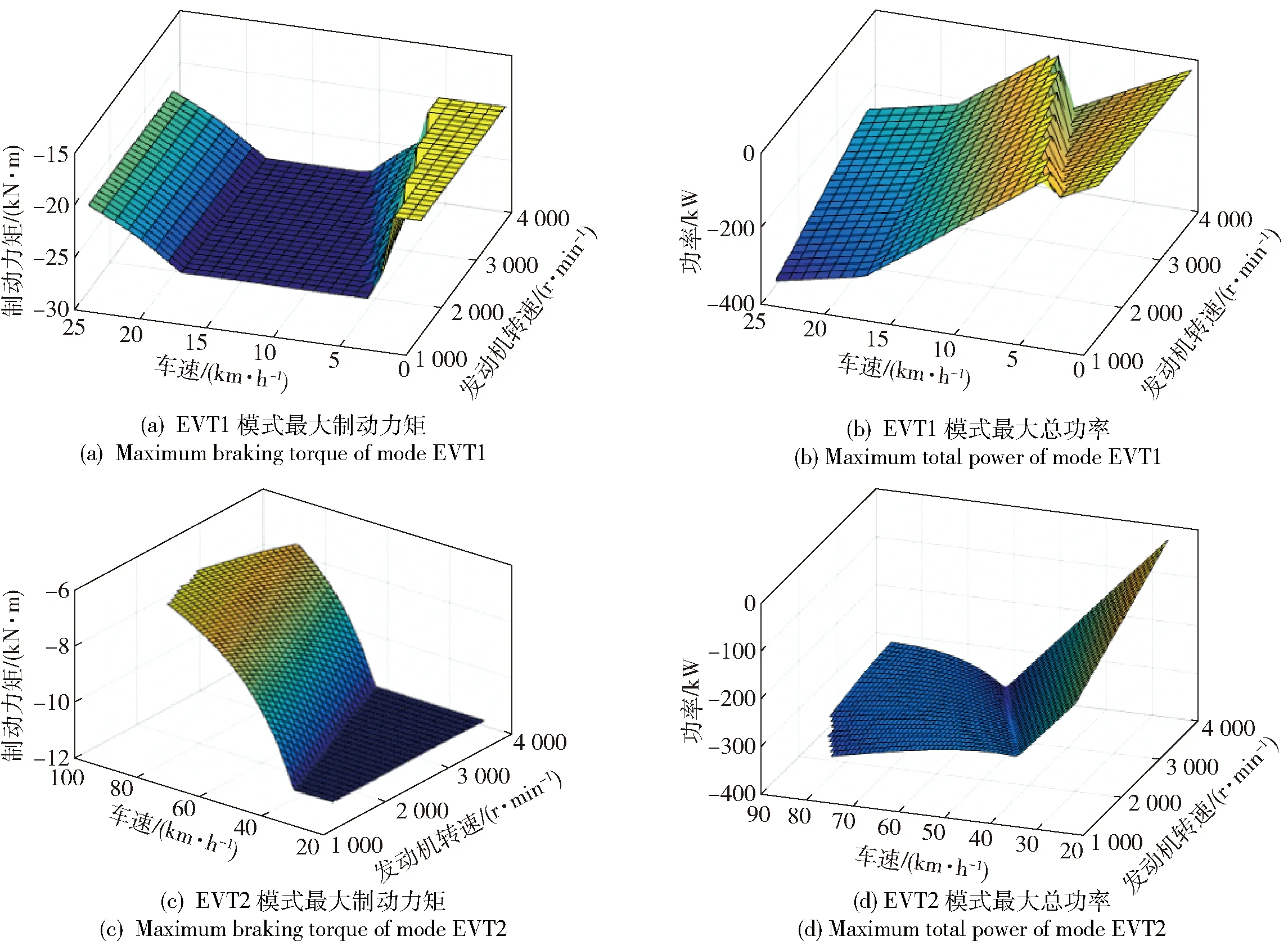
圖6 電機制動力特性Fig.6 Motor braking force characteristics

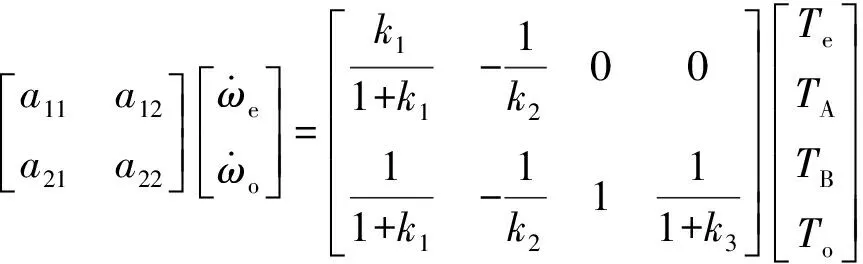
(13)

(14)

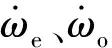
發動機、電機A、電機B工況約束如下：

(15)

式中：ωe,min、ωe，max分別為發動機最小轉速和最大轉速；Te，min、Te，max分別為發動機工作轉矩限值；ωm0、ωm,max分別為電機基速和額定轉速；ωκ、Tκ(κ=A、B)分別為兩個電機的實際轉速和轉矩；Pm,max為電機最大輸出功率。

聯立(13)式、(14)式和(15)式，可計算出雙電機復合制動特性如圖6所示。

2 控制策略設計

為緩解機械制動器工作強度，同時回收制動能量，設計了可變分配比例的并聯式復合制動結構[22]，如圖7所示。并聯式制動分配策略根據制動踏板計算總制動力，采用動態協調方法控制機械和電機兩種制動系統之間制動力的分配。在低制動強度條件下電機制動力占比較大，隨著制動強度升高，電機制動力進入飽和區，機械制動力占比增加。

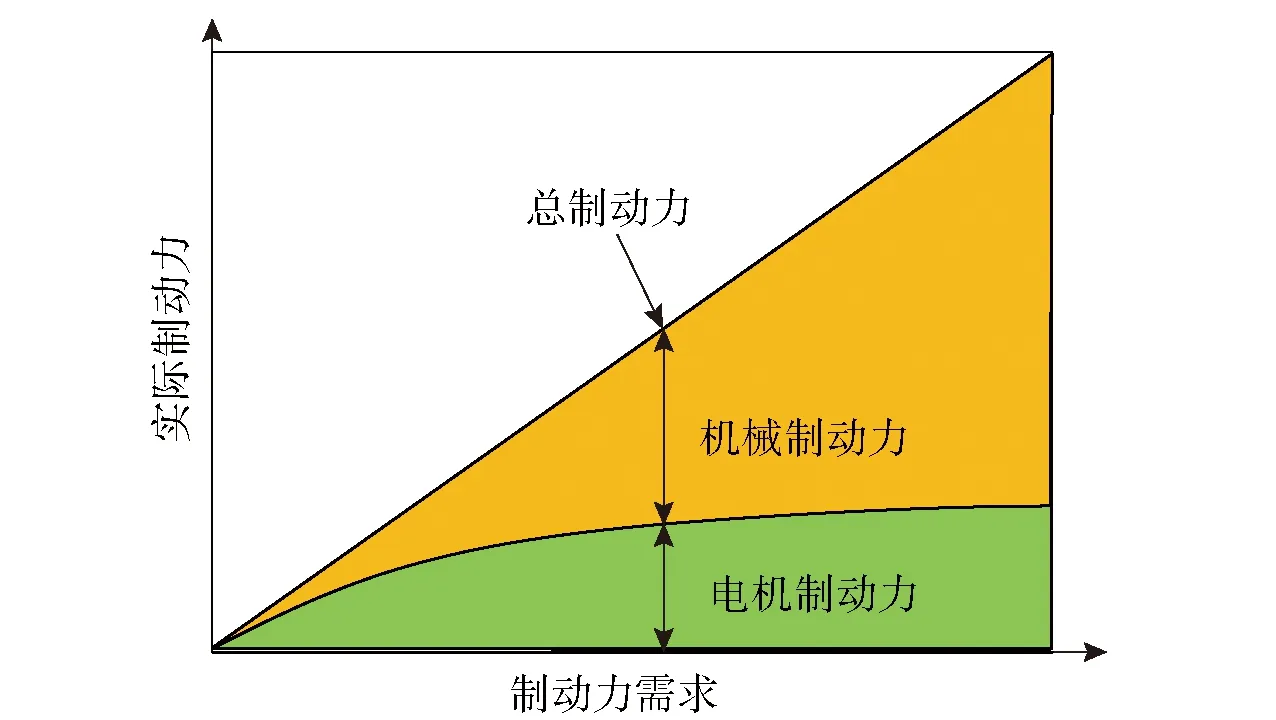
圖7 可變比例的并聯式機電聯合制動分配策略Fig.7 Braking distribution strategy with variable proportion

總制動力需求受履帶- 地面最大附著力限制，行駛過程中地面附著系數的時變特性導致地面制動力峰值波動，路面附著系數不足時主動輪易抱死，導致履帶拖滑車輛失穩。本文基于路面附著系數識別，提出電機制動飽和度模糊控制方法，設計分層制動控制器，以確保全路況條件下控制策略的有效性。

機電聯合制動系統總體控制框架如圖8所示。圖8中，Tb1為駕駛員意圖制動力矩，Tb2為最優滑移率控制輸出力矩，k為電機制動飽和度，TA，max、TB，max分別為當前車輛運行狀態下電機A、B可提供的最大制動力矩，未達到目標制動力矩的部分由機械制動器來進行提供。

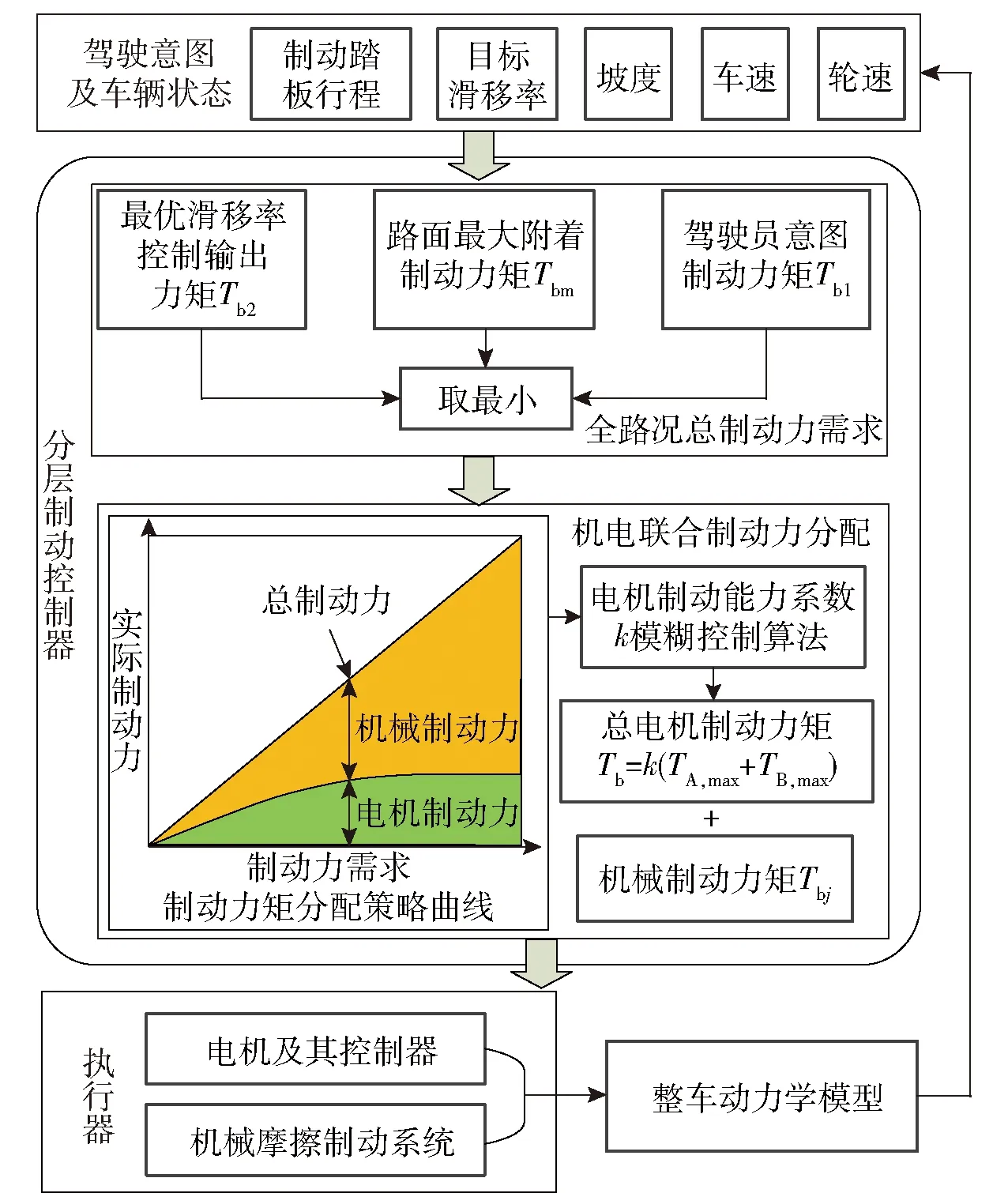
圖8 機電聯合制動控制框架Fig.8 Control block diagram of electromechanical braking

上層控制器根據車輛狀態和駕駛意圖計算附著條件約束下全路況整車需求制動力，下層控制器基于模糊控制方法計算總電機制動力分配系數，并實時求解機械制動力矩，最后向執行器輸出機電制動力矩控制指令。

2.1 總需求制動力矩

總制動力需求取決于駕駛員意圖制動力矩Tb1、路面最大附著制動力矩Tbm和最優滑移率控制輸出力矩Tb2三者之間的大小關系，即

Tb=min{Tb1,Tbm,Tb2}

(16)

駕駛員意圖制動力矩由制動踏板開度決定，即

(17)

式中：δ、δ0、δmax分別為制動踏板實際行程、最小有效行程和最大有效行程。

由(5)式可知，路面最大附著制動力矩Tbm為

Tbm=mgμ

(18)

針對路面附著不足導致履帶滑移失穩問題，采用滑模變結構控制算法進行滑移率控制，計算最優滑移率控制輸出力矩Tb2。

選取滑模變結構切換函數為

Θ=λ-λobj

(19)

式中：λobj為目標滑移率，當路面種類不變時λobj為常數。

履帶滑移率為

(20)

聯立(16)式和(17)式，并對(16)式求導，可得

(21)

為縮短趨近時間、減小抖振現象，采用冪次趨近率和等速趨近率相結合的混合趨近率[23]如下

(22)

式中：ε表示系統運動點趨近切換面的速率，ε>0；1>α>0；sat(·)為飽和函數；電機制動飽和度k定義如下，

(23)

Tm為實際輸出電機制動力矩。

由(3)式可寫出如下關系式：

(24)

(24)式代入(21)式，與(22)式聯立，可求解最優滑移率控制輸出制動力矩Tb2，得到

(25)

2.2 機電聯合制動分配策略設計

基于雙電機制動性能邊界及電機制動飽和度設計機電聯合制動控制策略。以制動強度z、SOC、車速v作為輸入，電機制動飽和度k作為輸出，制定控制規則如下：

1)緊急制動時，目標制動力矩大，采用機電復合制動，盡可能多地提供制動力矩；中度制動時，電機制動飽和度稍大，可充分回收制動能量；輕度制動時，目標制動力矩較小，可單獨采用電機制動。

2)當SOC較低時，盡量使用電機制動充電；當SOC水平較高時，應減少或停止電機制動。

3)當車速較高時，機械制動器摩擦劇烈，為減輕機械制動器使用壓力、避免熱衰退，電機制動保持較高飽和度；當車速較低時，EVT1模式發電功率小，回收制動能量有限，為保證制動可靠性，需要降低電機制動飽和度。

將制動強度z、車速v、SOC和電機的制動飽和度k分別進行歸一化，并分割為3個、5個、4個、5個語言變量，論域為[0，1]。由此得到分割后的變量模糊集合如表3所示。

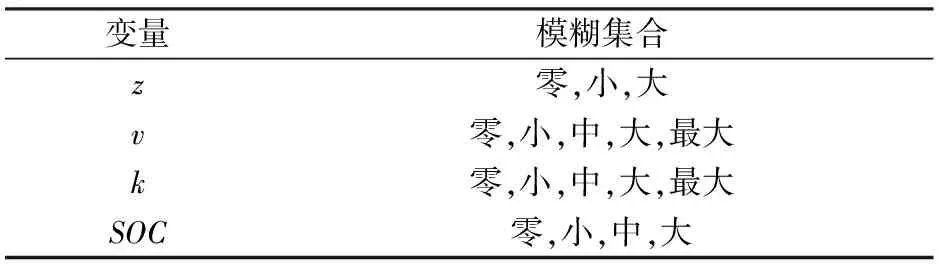
表3 變量模糊集合Tab.3 Variable fuzzy sets

基于上述3個基本原則，考慮雙電機復合制動特性，優先保證制動性能，并根據當前情況盡可能減少機械制動器載荷，同時提升制動能量回收率，根據表3可制定模糊規則60條。

3 控制參數識別與優化

3.1 路面附著系數識別

在非公路條件下，路面附著條件變化頻繁，地面最大制動力估計的準確性依賴于路面附著系數的辨識精度。本文采用擴張型狀態觀測器[24]識別路面附著系數μ。

對于線性控制系統

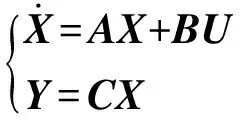
(26)

式中：X為狀態變量；U為系統輸入；Y為系統輸出；A、B、C分別為系統矩陣、輸入矩陣和輸出矩陣。

構造出以下新的系統

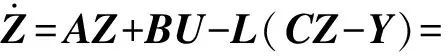
(27)

式中：Z為觀測器狀態變量；L為觀測器增益矩陣。

若存在矩陣L，使矩陣(A-LC)為李亞普諾夫穩定矩陣，則狀態Z可以估算原系統狀態變量X。系統(26)式可作為原系統(23)式的狀態觀測器，寫作

(28)

式中：e為系統的輸出誤差。

由(24)式履帶車輛動力學模型，有

(29)

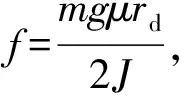
(30)

μ為非線性變化的量，可得非線性系統

(31)

由(28)式可得如下形式擴張型狀態觀測器[25]

(32)

令l1=-β1φ1(e),l2=-β2φ2(e)，β1、β2為觀測器的增益系數，φ1、φ2為連續函數。則(32)式變為

(33)

當eβ2φ2(e)≥0且eβ2φ2(e)≥0時，可以確保觀測器的輸出信號z1、z2分別為x1、x2的觀測值。

為避免高頻震顫現象，將函數φχ(e)(χ=1，2)取為在原點附近具有直線段的連續冪函數fal(e，αχ，γ)，

(34)

式中：γ為線性段的區間長度。

擴張型狀態觀測器(33)式變為

(35)

故有

(36)

可計算得到路面附著系數的估計值為

(37)

在建立擴張型狀態觀測器的基礎上，需要選取α1、α2、β1、β2等參數，αχ按(38)式選取

(38)

在fal函數中，一般取γ=5h，h為系統仿真步長，h的大小與被擴張狀態的幅值M相關，按照h=0.25M-1進行取值。由(38)式可得α1=1，α2=0.5，M=2mgrd/J，故有

(39)

利用帶寬的概念，使用二項式的展開式系數來確定狀態觀測器的增益參數[26]；根據擴張狀態觀測器參數與斐波那契數列之間的關系[27]，并給出了h-1的冪次形式經驗公式如下：

(40)

在實際應用中，由于具體研究對象和系統的不同，通常把經驗公式計算的值作為參考值，再通過數值仿真在參考值附近尋找合適的參數。優化參數后取β1=300，β2=2 000。

在實際過程中，履帶車輛行駛的路面往往是多種復雜道路，例如由耕地路面跨越柏油路面再進入耕地路面這種附著系數突變的工況，為驗證設計觀測器的有效性，在附著系數突變的堅實土壤路面工況下進行制動仿真分析，取初始車速v0=36 km/h，仿真結果如圖9所示。

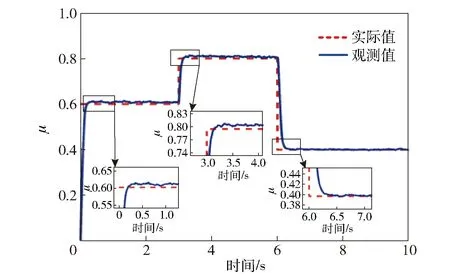
圖9 變路面附著系數觀測結果Fig.9 Observation results of variable road adhesion coefficient

由圖9可知，在附著系數突變的路面上所設計觀測器能準確識別路面附著系數，分別在0.28 s、3.24 s、6.26 s處到達穩定并收斂至實際值0.5、0.7和0.3，平均響應速度為0.26 s，路面附著系數觀測值和路面附著系數實際值誤差小，表明該算法識別速度快，精度高。

3.2 分配策略參數優化

將制動強度z、車速v、電池SOC 3個參數采用三角形隸屬度函數，對于模糊控制器的輸出電機制動飽和度k的隸屬度函數采用高斯型函數。將隸屬度函數參數化，如圖10所示。

采用遺傳算法分別對圖10中制動強度z、SOC、車速v的隸屬度函數參數a1～g1，a2～i2，a3～f3等參數進行優化。

選取電機制動飽和度k值的累積作為目標函數，種群數目設置為200，適應度函數選取為

(41)

遺傳算法優化隸屬度函數流程如圖11所示。

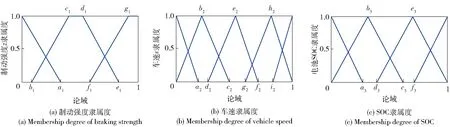
圖10 隸屬度函數參數化圖Fig.10 Parameterization of membership function

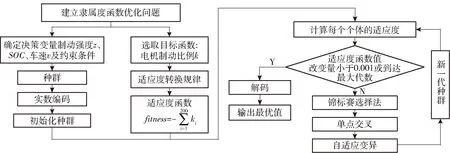
圖11 遺傳算法優化隸屬度函數流程圖Fig.11 Flow chart of membership function optimization based on genetic algorithm

選擇操作采用錦標賽法，在種群中抽取數量為n的個體進行比較，獲得適應度最高的個體，將其遺傳到下一代中，重復該操作使種群規模與初始規模一致。采用單點交叉方法，交叉概率取0.8。為增加種群的多樣性，同時提高算法的局部搜索能力變異操作，采用自適應變異方法。優化結果如圖12所示。

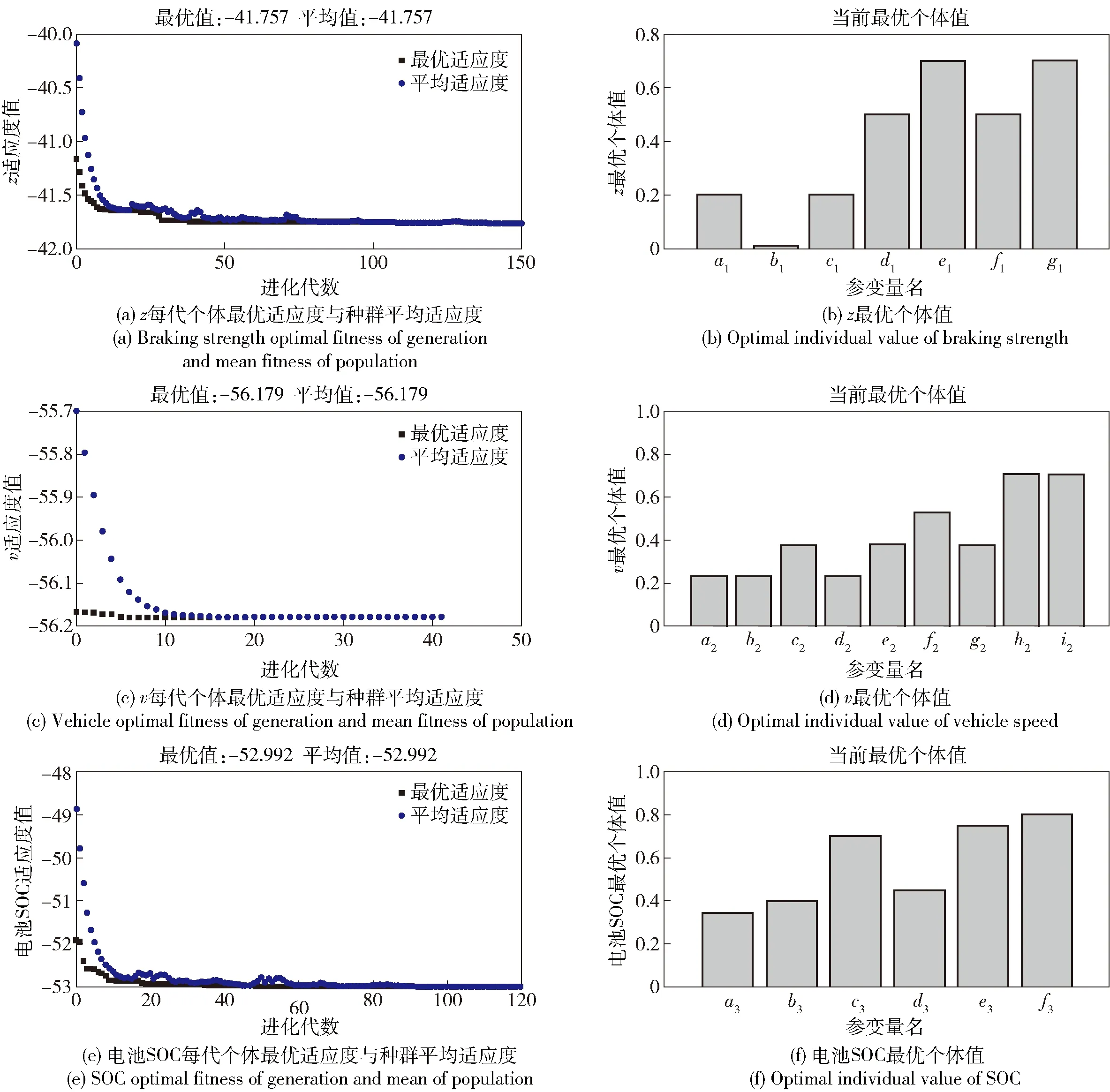
圖12 遺傳算法優化結果Fig.12 Optimization results of genetic algorithm

由圖12可知，在第82代左右到達穩定，在達到150代最大迭代次數時停止迭代，此時第150代中個體最優適應度為41.757，種群平均適應度為41.757。優化后的隸屬度函數結果如表4所示。

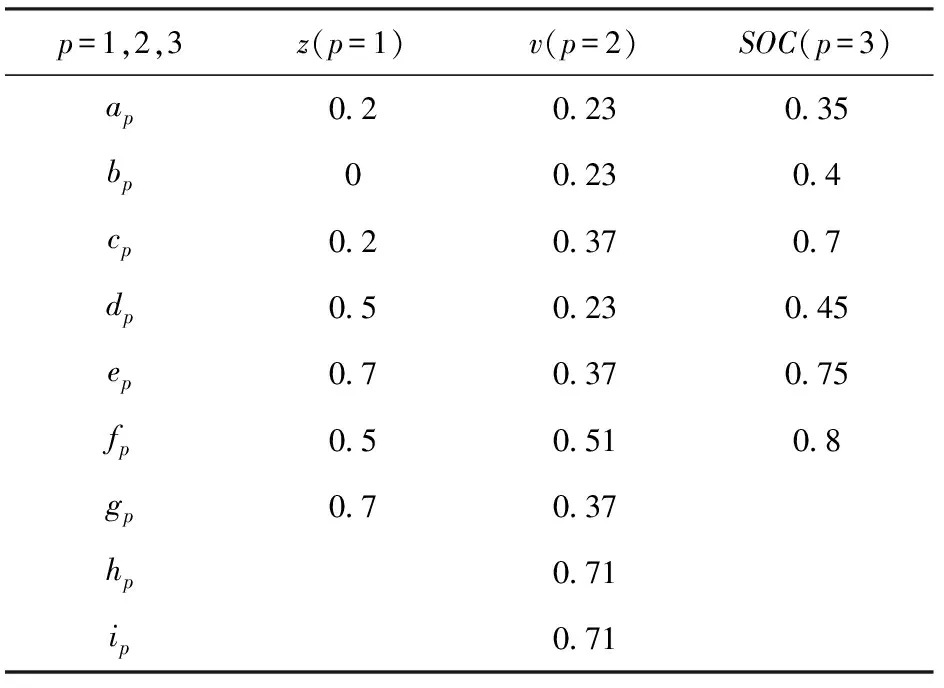
表4 隸屬度函數優化結果Tab.4 Optimization results of membership function

優化后隸屬度函數圖形如圖13所示。電機制動飽和度k隨歸一化車速- SOC、k隨車速- 制動強度、k隨SOC- 制動強度的變化如圖14所示。

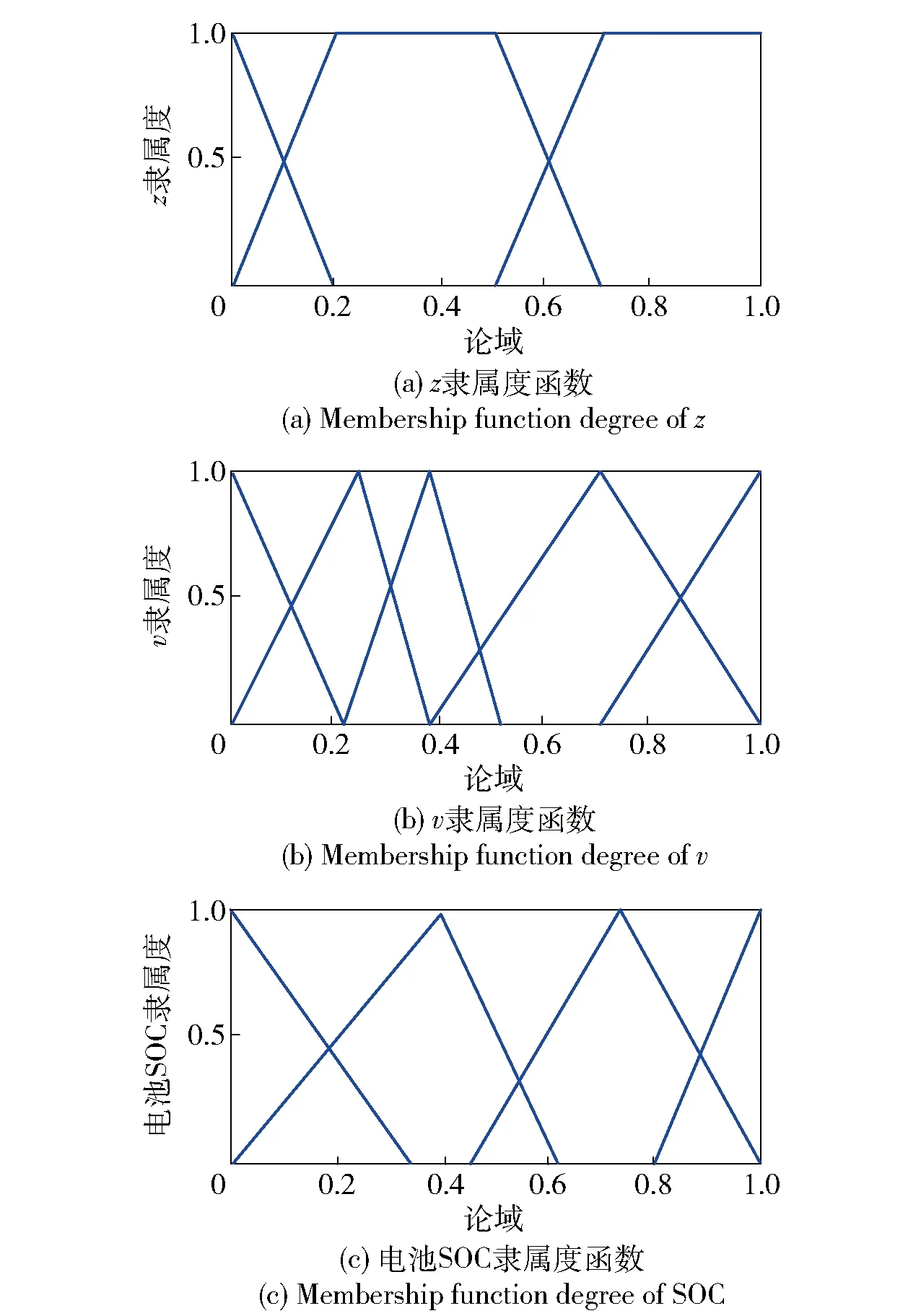
圖13 優化后隸屬度函數Fig.13 Membership function after optimization

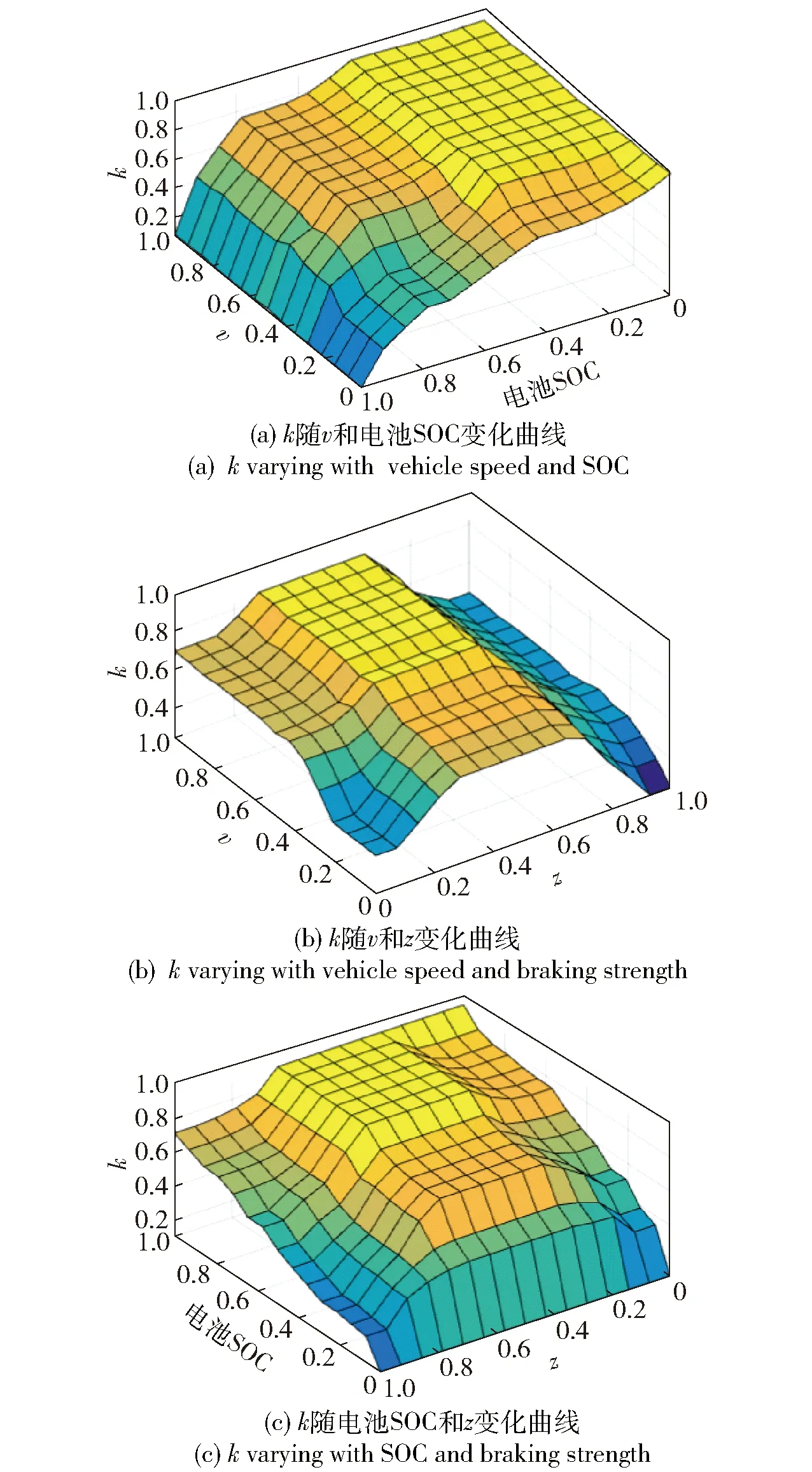
圖14 履帶車輛機電聯合制動模糊規則圖Fig.14 Fuzzy rule diagram of electromechanical braking of tracked vehicle

4 控制算法驗證

為了驗證混合動力履帶車輛機電聯合制動控制策略的有效性和實時性，利用仿真實驗及硬件在環平臺進行驗證。選擇高速緊急制動工況進行模擬，制動初速度為85 km/h、制動踏板開度為95%。

仿真結果如表5所示，從中可見電機制動比例變化范圍為4.3%～14.3%，電機制動比例平均值為8.96%，證明電機制動可以有效輔助機械制動，降低機械制動器使用強度。

表5 緊急制動仿真結果Tab.5 Simulation results of emergency braking

制動過程如圖15所示。圖15(a)表明經過4.5 s車速減為0 km/h，制動效果良好。制動力矩變化見圖15(b)，電機制動力矩快速響應目標制動力矩，初始階段機械制動力矩受作動器影響有0.25 s延遲；0.25 s以后，目標制動力超出當前車輛狀態下地面最大制動力，總制動力目標按照最大地面制動力輸出，整車滑移率逐漸上升(見圖15(c))；0.4 s滑移率到達目標控制區域，目標制動力矩開始按照滑移率控制策略執行，總制動力矩小幅度波動。0.65 s時，整車滑移率開始穩定在0.27，總制動力矩保持穩定。

車輛在3.5 s時由EVT2模式切換至EVT1模式，電機制動力矩突變，電機A、電機B總制動力矩升高。初始階段，電機制動飽和度k較大，這是由于電池SOC較低，車速較高，制動強度大。車速繼續下降，EVT1模式下總的發電功率較小(見圖15(d))，回收制動能量有限，為保證制動可靠性，電機制動飽和度變小。電制動飽和度變化趨勢合理，與制定聯合制動策略基本原則相符合，說明模糊控制規則設計合理。

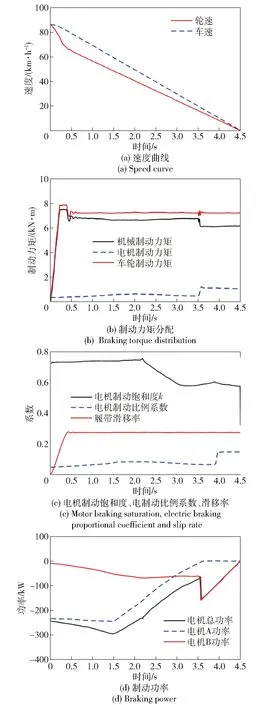
圖15 初速度85 km/h緊急制動仿真結果Fig.15 Simulation results of emergency braking (v0=85 km/h)

將仿真控制器算法通過代碼自動生成，下載到快速原型控制器RaidECU中。將電機及其控制器、耦合機構，機械制動器等機械系統以及履帶車輛和輪- 履- 路等動態模型下載到下位機系統，通過總線與控制器通訊。硬件在環實驗結果如圖16所示。

對比圖16和圖15可知，制動過程中，制動力矩和電機制動功率吻合較好，只在模式切換過程中出現較大波動，結果表明：所設計的全工況機電聯合制動控制算法實時性較好，能快速響應制動需求，并有效回收制動能量。

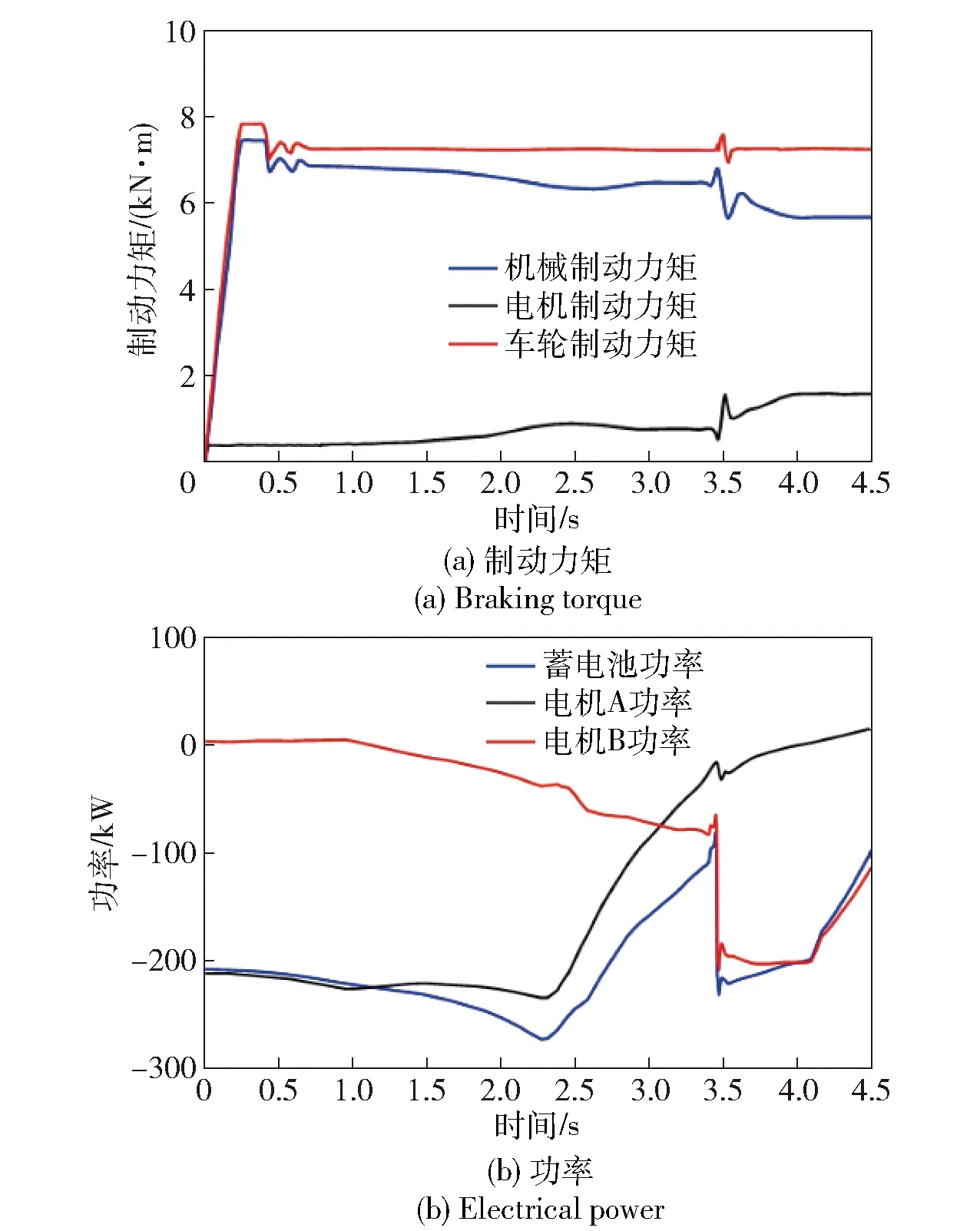
圖16 硬件在環實驗結果Fig.16 Results of Hardware-in-the-loop test

5 結論

本文以混聯式混合動力履帶車輛為對象，研究全路況機電聯合制動控制策略并進行了仿真驗證。得出主要結論如下：

1)應用擴張型狀態觀測器理論設計路面附著系數觀測器可以有效識別履帶車輛路面動態附著系數。算法速度快，精度高，穩定可靠，所識別的路面附著系數可用于機電聯合制動策略制定。

2)高速緊急制動仿真表明，制動開始0.5 s內滑移率穩定在最佳滑移率0.2左右，所設計的滑模控制算法可以有效控制低附路面上緊急制動工況的履帶滑移率。

3)以電機制動能力飽和度為控制目標的機電聯合制動控制算法充分考慮了制動強度、車速、電池SOC等因素對制動能量回收的影響，有效融合了能量回收效率和電機穩定性指標，解決了底層機械/電機制動力的協調分配問題。