基于UR5機械臂的軌跡跟蹤控制算法研究

王佳　胡旭曉　吳躍成

摘? 要：為了在現有基礎上提高機械臂軌跡跟蹤控制的精度，采用自適應模糊反演控制算法對六自由度機械臂UR5進行軌跡跟蹤控制算法研究。用拉格朗日法對UR5機械臂進行動力學建模以避免系統的不確定因素影響。由于UR5機械臂滿足Pieper準則，故對其進行模型簡化，減少運算量，并用拉格朗日法對前兩個自由度進行動力學方程推導，該算法在角位移和角速度跟蹤方面都表現出了很好的性能。

關鍵詞：UR5;模型簡化;拉格朗日法;軌跡跟蹤;自適應模糊反演控制

中圖分類號：TP241.2? ? ?文獻標識碼：A

Research on Trajectory Tracking Control Algorithm based on UR5 Manipulator

WANG Jia， HU Xuxiao， WU Yuecheng

Abstract： In order to improve the accuracy of manipulator trajectory tracking control on the existing basis， this paper proposes to study the trajectory tracking control algorithm of 6-DOF （degree of freedom） manipulator UR5 by using the adaptive fuzzy inversion control algorithm. The dynamic modeling of UR5 manipulator is established by Lagrange method to avoid the influence of uncertain factors of the system. Since the UR5 manipulator meets the Pieper criterion， its model is simplified to reduce the amount of computation， and the dynamic equations of the first two degrees of freedom are deduced by Lagrange method. The algorithm shows good performance in angular displacement and angular velocity tracking.

Keywords： UR5; model simplification; Lagrange method; tracking; adaptive fuzzy inversion control

1? ?引言（Introduction）

隨著工業技術的發展，機械臂逐漸成為工業領域自動化水平最高的科技產品之一[1]。在處于確定環境下的生產中，它可以代替人進行繁重的勞動，以實現生產的機械化和自動化并提高產品的質量和生產效率，在有害環境下作業還能夠保障人身安全。但當環境發生變化或變得復雜而無法精確測量機械臂的各個參數，以及難以建立精確的動力學模型時，這些不確定因素均會限制機械臂的運動控制，尤其是在機械臂自主進行接觸式操作如切割、電焊等方面將會面臨非常大的挑戰[2]。PID或PD控制[3]是目前工業機器人應用最為廣泛的一種控制算法，雖易于操作但難以保證機械臂的動態性能，當啟動時的輸出力矩過大時容易造成機械臂損壞。本文選用不需要精確模型的控制策略進行跟蹤控制研究，避免了因模型建立不夠精確而降低控制精度的問題。

2? UR5機械臂動力學模型的建立（Dynamic model establishment of UR5 manipulator）

2.1? ?UR5機械臂簡介

UR5機械臂[4]是由Universal Robots公司開發的靈活、輕型的六關節工業機器人，由六個關節和擠壓鋁管組成，所有關節均為轉動關節。關節1—6分別命名為：機座、肩部、肘部、手腕1、手腕2和手腕3。其中機座可以用來確定機器臂的安裝位置。UR5機械臂質量較小（僅18.4 kg），可以方便地在生產場地移動，而且不需要煩瑣的安裝與設置就可以迅速地融入生產線中，與員工交互合作，并可處理最大5 kg的有效負載。UR5機械臂編程可通過教學編程模式實現，用戶扶住機械臂，手動引導機械臂按所需的路徑及移動模式運行一次，它就能自動記住移動路徑和模式。UR5機械臂可通過一套獨特的、友好的圖形用戶界面進行操作，在觸摸屏幕上有多種功能供用戶選擇。任何重復性的生產過程都能夠使用它并從中受益，這使得UR5機械臂的應用十分廣泛。

UR5機械臂前三個關節主要控制末端的位置，后三個關節主要控制末端的姿態[5]。通過各個關節之間的協調運動，它可以在其工作范圍內任意移動。UR5機械臂實物圖如圖1所示。

2.2? ?模型簡化

由于通用工業機械臂滿足Pieper準則[6]，即后三個關節軸相交于一點，因此，前三個關節主要完成機械臂末端位置運動，且動力學參數值（轉動慣量、質量等）較大，非線性效應比較明顯;后三個關節主要完成機械臂末端位姿調整，動力學參數值較小。在誤差允許范圍內，考慮將六自由度機械臂模型簡化為前三個自由度機械臂模型，并將后三個關節看作動力效應的外部干擾，對其進行動力學分析。實驗表明，當只考慮機械臂前三個關節時其動力學特性與考慮全部六個關節相比不失一般性，且誤差較小。這不僅減少了計算量，對于參數辨識來講，減少了待辨識的參數，也使獲得相對精確較高的動力學模型變得更加容易。簡化模型如圖2所示。

2.3? ?拉格朗日法建立動力學方程

拉格朗日力學[7]與牛頓力學完全等效，其優勢在于只需要寫出拉格朗日量，就可由簡單求導得到完整的動力學微分方程而無須進行受力分析;方程的形式不隨廣義坐標的選取而改變;無須解方程即可得到一些守恒量。

利用牛頓力學分析動力學時，在分析的過程中可以知道所有連桿生成運動的方向以及大小，但分析太過復雜。UR5機械臂動力學模型是一個非常復雜的非線性模型，若使用牛頓力學，出錯的機會就會大大提高。而拉格朗日力學是基于能量項對系統變量及時間的微分方法，是以能量的角度來看待系統的。

歐拉-拉格朗日運動方程為：

（1）

其中，L是拉格朗日函數，K是系統動能，P是系統勢能。

系統的拉格朗日方程為：

（2）

其中，為機械臂關節i的力矩，和為關節位置和速度。

最終寫成如下公式：

（3）

其中，M為機械臂的慣性矩陣，是與角加速度相關的項;C為科氏力與離心力項矩陣，是與角速度有關的項;G為重力項，不受角速度和角加速度的影響，僅與機械臂所處位置有關;為外部輸入力矩，q為機械臂的角位移。

（4）

（5）

其中，A為離心力系數，B為科氏力系數。

（6）

（7）

（8）

由于機械臂的動力學模型還受到外界干擾的影響，令外界干擾為d，動力學模型可建立為：

（9）

假設系統參數是未知但有界的，且系統具有以下特性：

（1）慣性矩陣是正定對稱矩陣，且有界，即存在，;

（2）慣性矩陣、向心力和科氏力矩存在以下關系：

（10）

3? 自適應模糊反演控制算法（Adaptive-fuzzy-backstepping control algorithm）

3.1? ?反演控制算法

反演控制算法是一種非線性系統設計的方法[8]，它是將下一級的變量當作虛擬輸入作用在該一級系統上，同時根據上一級系統建立Lyapunov函數，實現系統穩定，直到最后一個系統實現控制，得到輸入量。反演控制算法保證在任何情況下存在Lyapunov函數，使得該系統穩定，同時利用該函數找到一個參考輸入，最終實現對輸入的推導和設計。

機械臂動態方程可寫為：

（11）

令，則動態方程可改寫為：

（12）

定義誤差：

（13）

（14）

式中，為虛擬控制量，通過選取，使得趨近0;為控制軌跡，為期望軌跡，為控制角速度。

取：

（15）

對于第一個子系統，Lyapunov函數為：

（16）

（17）

若為0，則第一個子系統穩定。

（18）

控制律設計為：

（19）

對于第二個子系統，Lyapunov函數為：

（20）

（21）

當時，第二個子系統穩定。

反演控制[9]算法具有如下優勢：

（1）其設計的控制器以及Lyapunov函數的過程都非常清晰明了，具有系統化、結構化的特點。

（2）對于高階的非線性系統也可以取得非常好的控制效果，消除了經典無源性設計中相對階是1的限制。

（3）不確定性要滿足匹配條件的要求，控制不確定非線性系統時有著明顯的優越性。

3.2? ?自適應模糊控制

模糊控制就是將模糊數學的基本思想和理論應用到控制的領域。模糊控制[10]的一般流程包括：

（1）確定模糊控制器的結構：確定控制器的輸入、輸出。

（2）定義輸入、輸出的模糊集。

（3）定義輸入、輸出的隸屬度函數。

（4）建立模糊控制規則。

（5）建立模糊控制集。

（6）進行模糊推理。

傳統的基于模型的控制方法非常依賴于精確的動態模型。但是對于UR5六自由度非線性的復雜系統來說，是很難實現精確控制的。而模糊控制不依賴于被控對象精確的數學模型，適合動態特性不易獲取的控制對象。同時，模糊控制是以人類的經驗積累為出發點的，且這種控制的魯棒性好，可以用于逼近參數不確定的各種線性和非線性系統的模型。

式（21）中，當時，，此時：

（22）

將式（19）代入式（22）中得：

（23）

式（23）中，包含機器人的建模信息。由于機械臂的精確動力學模型是很難建立的，因此我們采用自適應模糊控制，這種控制方式不需要精確的模型信息。假設是用來逼近的模糊系統。這里我們采用單值模糊化、乘積推理機和重心平均反模糊化。

假設模糊系統由N 條模糊規則構成，第 條模糊規則表達形式為：

： IF? is? and ... is ，then? is 。

（=1，2，…，N）

其中，為（j=1，2，…，n）的隸屬函數。

則模糊系統的輸出為：

（24）

其中，，，。

對于的模糊逼近，分別采用逼近（1）、（2）的形式，相應的模糊系統設計為：

（25）

（26）

（27）

其中，，。

定義最優逼近常量，對于給定的任意小的常量（>0），如下不等式成立：

設計自適應控制律為：

（28）

4? ?實驗結果及分析（Experiment analysis）

對UR5機械臂進行模型簡化后，并對前兩個自由度進行軌跡跟蹤控制，采用的控制算法為自適應模糊控制算法。

UR5機械臂動力學參數各個連桿質心位置及質量如表1所示。

表1 UR5機械臂動力學參數

Tab.1 Dynamic parameters of UR5 manipulator

連桿編號 xi/m yi/m zi/m m/kg Li/m

1 0 -1.93e-3 -26.51e-3 3.7 0.892

2 212.5e-3 0 113.36e-3 8.393 0.425

本文以UR5機械臂為研究對象，對UR5機械臂進行動力學軌跡規劃控制。設期望軌跡分別為、

。

系統的初始狀態為。外界擾動。

建立二自由度機械臂自適應模糊反演控制系統Simulink仿真模型，如圖3所示，其中control為控制器子程序，D1plant為運算實際軌跡子程序。

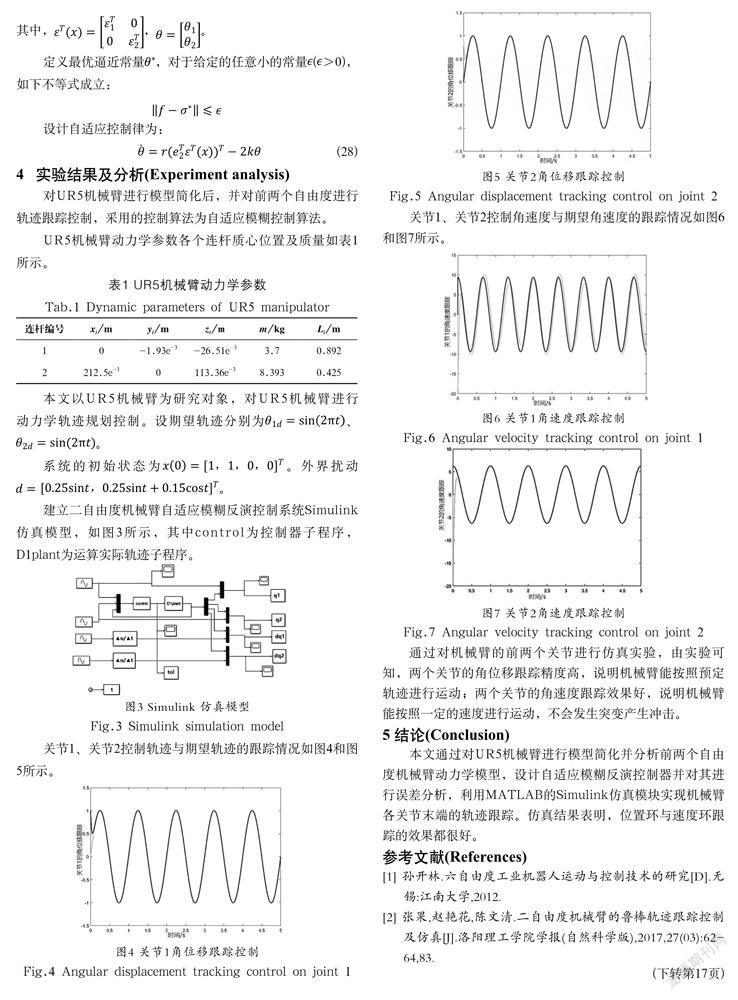
關節1、關節2控制軌跡與期望軌跡的跟蹤情況如圖4和圖5所示。

關節1、關節2控制角速度與期望角速度的跟蹤情況如圖6和圖7所示。

通過對機械臂的前兩個關節進行仿真實驗，由實驗可知，兩個關節的角位移跟蹤精度高，說明機械臂能按照預定軌跡進行運動;兩個關節的角速度跟蹤效果好，說明機械臂能按照一定的速度進行運動，不會發生突變產生沖擊。

5 結論（Conclusion）

本文通過對UR5機械臂進行模型簡化并分析前兩個自由度機械臂動力學模型，設計自適應模糊反演控制器并對其進行誤差分析，利用MATLAB的Simulink仿真模塊實現機械臂各關節末端的軌跡跟蹤。仿真結果表明，位置環與速度環跟蹤的效果都很好。

參考文獻（References）

[1] 孫開林.六自由度工業機器人運動與控制技術的研究[D].無錫：江南大學，2012.

[2] 張果，趙艷花，陳文清.二自由度機械臂的魯棒軌跡跟蹤控制及仿真[J].洛陽理工學院學報（自然科學版），2017，27（03）：62-64，83.

[3] 李巖，丁浩，孫中波，等.基于一種加速PD型迭代學習控制算法的機械臂軌跡跟蹤[J].科學技術與工程，2019，19（26）：265-269.

[4] 蔡肖肖.UR5型機器人的運動學分析與標定實驗研究[D].杭州：浙江理工大學，2017.

[5] 王海，付邦晨，薛彬，等.六自由度柔性關節機械臂的動力學分析[J].中國機械工程，2016，27（08）：1096-1101.

[6] 晁智強，王飛，李華瑩，等.六自由度工業機械臂動力學模型簡化分析[J].火力與指揮控制，2018，43（02）：112-115.

[7] 宋花.六自由度機械臂軌跡跟蹤控制[D].包頭：內蒙古科技大學，2020.

[8] 馬宇豪.六自由度機械臂避障軌跡規劃及控制算法研究[D].北京：中國科學院大學（中國科學院西安光學精密機械研究所），2019.

[9] PIKASO P， MUKHERJEE V， HINSERMU A， et al. Generalized adaptive backstepping sliding mode control for synchronizing chaotic systems with uncertainties and disturbance[J]. Mathematics and Computers in Simulation， 2021， 190（01）：793-807.

[10] CHEN Z， WANG D， DAO G H， et al. Environmental impact of the effluents discharging from full-scale wastewater treatment plants evaluated by a hybrid fuzzy approach[J]. Science of the Total Environment， 2021， 50（08）：790-798.

作者簡介：

王? 佳（1998-），女，碩士生.研究領域：六自由度機械臂軌跡跟蹤控制.

胡旭曉（1965-），男，博士，教授.研究領域：圖像處理，機器人軌跡跟蹤控制.

吳躍成（1966-），男，博士，副教授.研究領域：人機交互.