改進直通濾波SAC-IA粗配準算法

宮德寧,吳琳娜,李榮華,盧祺

(1.大連交通大學 機械工程學院，遼寧 大連 116028；2.上海宇航系統研究所，上海 201109)

隨著航天技術的飛速發展，空間在軌服務成為當前亟需技術，主要包括輔助變軌、碎片移除、在軌燃料加注與延壽、在軌裝配和在軌維修等.空間目標三維重建是空間在軌服務的關鍵，三維重建技術主要包括可見光序列圖像和激光雷達方法.Yingying Gu[1]通過單目相機測量，提出了一種在復雜光照條件下可以穩定提取目標圖像投影角度的圖像處理方法.劉玉[2]驗證激光雷達的航天器相對位姿測量技術方法合理可行,測量精度高,可滿足近距離操控中相對導航任務需求,對國內后續開展工程應具有較大參考價值.尹芳[3]針對激光3D點云數據跟蹤配準中產生的累積誤差問題，提出了位姿圖優化的SLAM技術框架的方法.點云數據配準是空間目標三維重建必要途徑，準確的點云配準可以提高三維重建精度.

點云配準分為粗配準[4〗和精配準[5].粗配準也叫初始配準，用于處理兩幅未知點云位姿信息，為精配準提供良好的初值.近年來為了提高配準精度，越來越多的學者開始研究粗配準算法.Rusu[6]提出了計算點云特征描述的子方法，描述了中心點與其領域范圍點之間的空間差異，形成點特征直方圖(Point Feature Histograms,PFH).R.B.Rusueta[7]提出了一種基于FPFH特征的配準算法，該算法不僅提高了點云配準精度，也顯著性提高了點云配準的效率.隨著配準算法的進一步研究，NDT算法[8]、3DSC算法[9]和4PCS算法[10]開始得到廣泛應用.Chen[11]首次在點云配準中運用RANSAC算法，繼而Rusu[6]通過快速點特征直方圖(Fast Point Feature Histograms,FPFH)描述子和RANSAC原理，提出了SAC-IA(Sample Consensus Initial Alignment)算法.

利用NDT、3DSC、4PCS和FPFH等傳統算法實現了點云的粗配準，對部分點云數據能夠得到較好的結果，為精確配準提供較好的初始旋轉矩陣，但對于衛星點云等平面特征多且特征單一的特殊點云模型，容易產生異部分誤匹配，導致粗配準失敗.針對以上問題，本文提出改進直通濾波SAC-IA粗配準算法，首先對點云數據處理時，先需要進行離群點與噪聲的去除；其次采用PCA算法計算點云數據中心點，去除均值，得到協方差矩陣，從而得出特征值以及特征向量；然后特征向量方向為主成分方向規定成分方向為Z軸進行坐標變換，再對Z軸方向進行直通濾波，保留衛星主體部分，去除太陽能帆板，再進行主體部分下采樣濾波，能有效提高配準精度；最后計算2個待配準點云的法向量，使用Kd-Tree樹結構對點云的FPFH特征進行加速計算，得到目標點云和待配準點云的FPFH特征.再根據2個點云相似的FPFH特征，使用SAC-IA算法求解變換矩陣，同時對前期PCA算法處理后的點云進行逆變換，求累積矩陣變換，完成點云粗配準，具體點云粗配準路線見圖1.

圖1 配準路線圖

1 改進點云直通濾波

根據真實衛星尺寸進行1∶1三維建模，經MeshLab軟件處理三維模型，生成衛星點云數據，最后在通過MATLAB對數據仿真，得到局部可視點云，仿真過程中加入噪點，模擬真實數據情況.在處理點云數據時，大多數需要通過濾波重采樣來對點云進行預處理，在保留特征的前提下節省特征子計算時間，提高點云配準精度和時效性[12].考慮到衛星點云初始目標的太陽能帆板平面部分和目標點云衛星主體平面部分點云造成誤匹配，為了得到準確的點對對應關系，本文首先去除點云離群點，然后采用PCA變換分析方法估算點云的法向信息，獲得點云的三個主方向，獲取質心，求得協方差矩陣，從而求解出矩陣的特征值和特征向量，特征向量即為主方向.接著校正主方向垂直，變換矩陣為M，對點云進行坐標變換，這樣無論衛星在任何位姿下，都能準確地保留中主體部分.計算過程如下：

(1)求每個維度的平均值

(1)

(2)

(3)

式中：N是點云中點的總個數.

(2)求協方差矩陣以及對應的特征值、特征向量

(4)

Cλ=μλ

(5)

利用矩陣知識，求協防差矩陣C的特征值λ和相對應的特征向量μ，特征向量為主方向.

(3)用(1)，(2)中獲得的點云主方向和質心，將輸入點云轉換到原點位置，且主方向與坐標系Z軸方向重合.再進行點云直通濾波，如圖2所示，因為衛星的點云主體寬度尺寸已知為A，所以直通濾波時選取濾波范圍A，剔除兩側太陽板，保留衛星目標的主體部分,點云數據通過對主體點云進行下采樣濾波處理，不僅提高了計算效率，而且能有效防止對應點對之間產生錯誤，提高準確率.

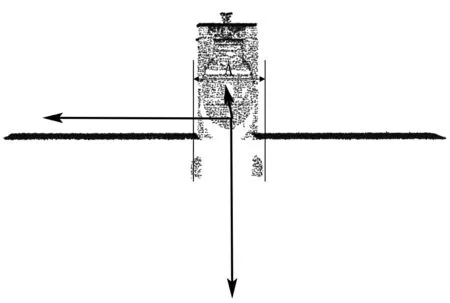
圖2 改進點云濾波圖

2 點云配準

在點云的初配準中，首先計算經過濾波處理衛星點云主體部分中每個點的FPFH，然后使用SAC-IA算法在目標點云中查找與待配準點云中具有相似FPFH特征的點，從這些相似點中構建對應點對應關系．計算旋轉變換矩陣，旋轉平移待配準點云完成配準.

FPFH是由PFH改進而來的，首先計算查詢點與鄰域點之間的關系，而不計算鄰域點與鄰域點之間的關系特征，接著再確定查詢點與鄰近點的理論復雜度.雖然FPFH沒有對近鄰點所有組合進行計算，可能會導致重要點對的丟失，但在進行權重和鄰近點的重新計算過程中，降低了信息復雜度，增加了適用性，有效提升運算速率.

FPFH在計算Pq和其k鄰域點Pk1～Pk5，構建每一個領域點的局部坐標系，分別計算出每個k領域點的四元組，獲得特征直方圖，不計算領域點與領域點之間的關系，得到簡化的點特征直方圖(Simple Point Feature Histograms, SPFH).如圖3所示，分別以Pk1～Pk5作為目標點尋找其k鄰域點并計算法向量、構建局部坐標系、獲得Pq和其鄰域點為目標點的SPFH.點Pq的FPFH特征計算公式為：

(6)

式中：Pq和Pk為相鄰點；ωk是Pq和Pk的距離權重.

在式(6)中，以Pq和其鄰域點Pk之間的距離作為權重.首先獲取衛星點云全部點的簡化特征直方圖，接著通過點云的簡化特征直方圖與鄰域點的SPFH值重新加權計算，最后得到衛星點云的快速點特征直方圖,如圖3所示.

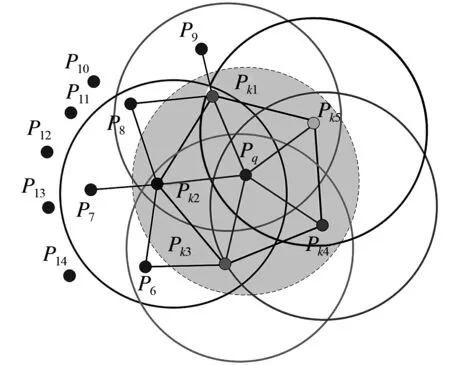
圖3 FPFH計算原理圖

計算完衛星主體部分特征描述子之后，通過采樣一致性初始配準算法(Sample Consensus Initial Aligment)來尋找兩幅衛星點云的對應點，從而得出旋轉平移矩陣.具體步驟如下：

(1)從待配準點云A′中選取m(m>3)個采樣點，規定采樣點之間的最小距離，能保證采樣點具有不同的快速點特征直方圖特征.

(2)查找待配準衛星點云A′的點與目標衛星點云B′中的點具有相似的快速點特征直方圖特征，選取相似特征的點云作為待配準點云與目標點云的對應點.

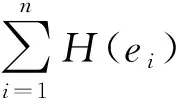
(7)

式中，ei為第i組對應點變換之后的距離差，L為預先給定值.

3 坐標變換

配準的結果不僅要從圖像得出，也要從最后得出的平移 、旋轉數據上體現，二者需要相輔相成，而坐標變換也是點云配準得到平移、旋轉誤差的重要途徑.本文在求初始點云跟目標點云之間的變換經過了兩次變換，首先是兩幅點云的主成分方向變換，然后是經過變換后的點云配準變換，所以求取初始點云與目標點云之間的位姿變換需要對兩次變換矩陣整體求逆變換，得到的矩陣是要求取的誤差矩陣.具體流程如圖4所示.

圖4 矩陣變換流程圖

其中點云A是初始點云，點云B是目標點云.最后配準過程輸出結果是矩陣P.在矩陣變換過程中，符合下列計算規則，其中C,D,E為可逆的4×4階矩陣：

(8)

(9)

(10)

如果CD=E，那么

(11)

在矩陣進行變換時，

CD=E?C=ED-

(12)

所以根據式(12)可以得出：

P=M×N×O-

(13)

4 結果與分析

本文實驗平臺配置如表1所示.

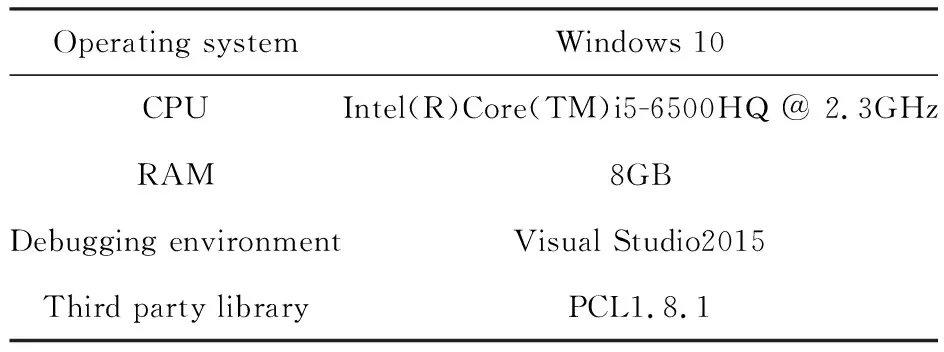
表1 系統環境配置

如圖5所示，采用了一組仿真數據自旋4.979章動5.103 7章動角56.68的第0幀和第5幀兩組可視點云進行實驗，兩組數據由于掃描數據時相機的站位不同，自身遮擋重疊部位點云數據無法顯示，不能得到全部點云.圖5中的原始點云數據有16 782個點，目標點云數據有19 054個點.

圖5 輸入點云模型

由于點云數據遮擋部分不同，形成的可視點云數據對應部分減少，增加配準難度，對效率和精度影響大.首先對點云進行主成分分析，接著對點云進行變換，最后對點云進行直通濾波，圖6(a)為處理后的原始點數據，圖6(b)為處理后的目標點云數據.

(a) 處理后的原始點云

(b) 處理后的目標點云圖6 直通濾波處理后的結果

為了驗證本文算法的有效性，跟傳統的3DCS、4PSC、FPFH、NDT粗配準算法進行比較.通過對比配準前后點云模型在X、Y、Z軸的旋轉誤差和平移誤差來判定配準精度，從而得出配準結果.為驗證算法的有效性，控制其他閾值對配準結果的影響，對仿真數據進行相同的濾波，去除離群點，進行配準，并記錄了不同點云配準方法完成衛星點云粗配準所需的時間和平移旋轉誤差，配準實驗效果如圖7所示.

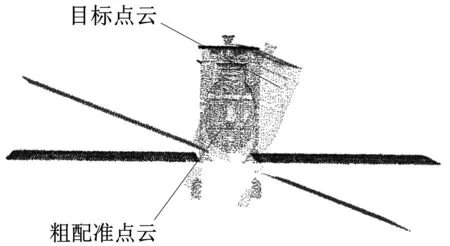
(a) 3DSC配準

在配準效率方面，通過點云配準所需要的時間來反應.實驗數據如表2所示.

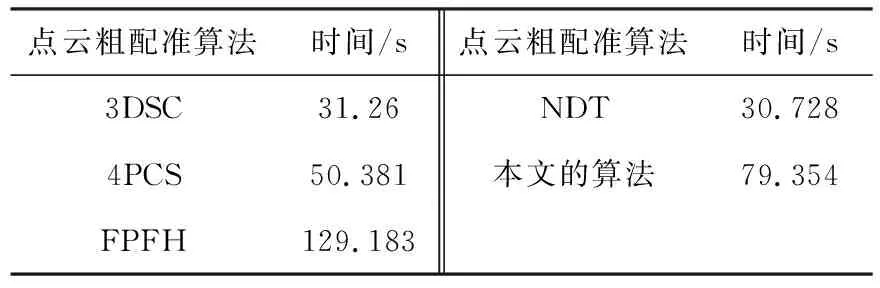
表2 配準時間表

在配準精度方面，通過不同坐標軸的旋轉誤差來反應，如表3和圖8所示.

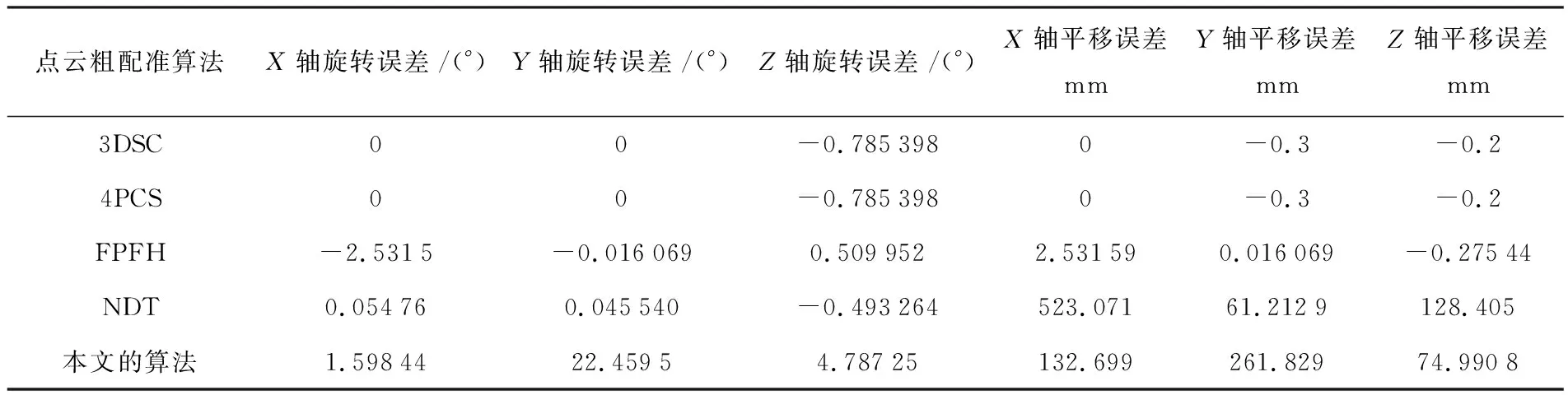
表3 誤差記錄表

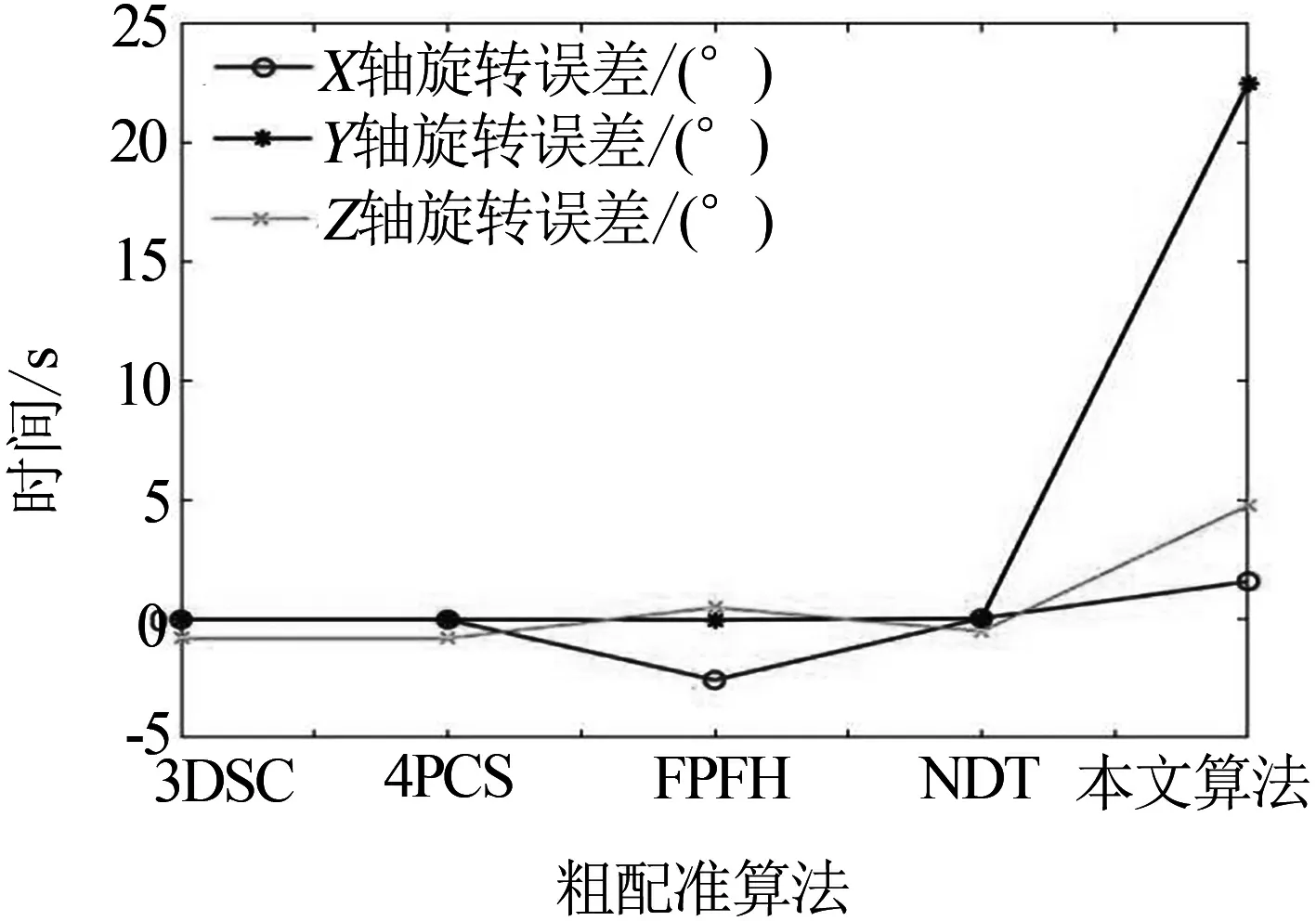
(a) 粗配準旋轉誤差

在基于局部特征的描述算法中3DSC的點云配準時間要明顯小于FPFH，由于快速點特征直方圖需要計算查詢點與鄰域點之間的關系，消耗時間長.3DSC需要計算出點云的曲面形狀特征，增加了計算量，由于點云的數量多，計算查詢點與領域點之間的關系消耗的時間要遠大于計算出點云的曲面形狀特征.衛星點云由于曲面特征少，平面特征較多導致3DSC計算形狀特征配準失敗；在基于全局特征的描述方法中4PCS需要計算兩幅點云共面的四點基，然后依據放射性不變的原理，進行剛體變化，衛星模型由于其特征大多數是直面特征，導致計算時間短，配準失敗；NDT計算正態分布是一個一次性的工作(初始化)，不需要消耗大量代價計算最近鄰搜索匹配點概率密度函數，在兩幅圖像采集之間的時間可以離線計算出來，配準效率高，但是精度低，受點云的模型影響大；本文提出的算法雖然在前期進行點云主成分分析和坐標變換時占用了時間，但是在后面配準過程中采用直通濾波后的點云數據，在保證足夠配準所需的特征前提下，大大減少了點云的數量，去除部分相似特征部分，如圖8所示，在不同算法的配準結果中，本文所提算法的配準效果最好，能提高效率和配準精度.由此可見，本文算法能夠對衛星點云，可以實現高精度、高效率的點云粗配準.

5 結論

針對衛星目標的幾何形狀特殊、平面特征多以及配準方法適合度低等問題，本文通過對SAC-IA粗配準算法的直通濾波改進，并跟傳統的粗配準算法進行比較，本文的算法能夠有效完成衛星點云粗配準工作；3DSC和4PCS由于衛星點云模型的特殊結構無法完成配準工作；FPFH和NDT雖然在配準效率方面較高，但是其精確性較低.首先對衛星點云的主成分分析，確定主成分方向，將點云主成分方向與Z軸重合進行坐標變換，再對其直通濾波保留衛星主體部分，接著對其進行粗配準，最后進行點云坐標變換.這樣不僅保證點云有足夠的特征進行配準，而且也能夠有效防止配準失敗和提高配準效率.