韌性視域下北極航行風險級聯效應分析

馬曉雪 何佩龍 喬衛亮 劉陽

(1 大連海事大學,公共管理與人文藝術學院,遼寧 大連 116026;2 大連海事大學,航運經濟與管理學院,遼寧 大連 116026;3 大連海事大學,輪機工程學院,遼寧 大連 116026)

0 引言

北極航線航行環境正醞釀重大變化并有望在夏季實現全線通航[1],國際社會對北極的關注度也因此變得越來越高。針對北極通航安全風險,目前已經形成了較為完整的研究體系。對于北極航線安全風險模糊性特征造成的認知障礙,李振福等[2]利用盲數理論提出了處理盲信息灰信息等不確定信息的方法;與之類似,后悔理論也被應用于北極航線安全風險分析中[3];另外,王銳等[4]借助灰色系統理論在處理不確定信息方面的優勢對北極環境數據中的確定性信息進行了分析。為更好地解決由北極安全風險動態性造成的認知困境,馬曉雪等[5]依托動態貝葉斯理論實現了對北極航線安全風險的動態把握。目前應用韌性理論來研究北極安全風險的成果并不多見,付姍姍等[6]依托韌性工程構建了涉及四因素五方面的極地船舶航行框架,為后續研究提供了參考。以上研究多從“人-機-環-管”的框架下認識船舶航行風險,將研究重點聚焦在風險及其后果上,未重點考慮應對風險的能力建設,且缺少對風險間耦合級聯效應的探討;鑒于此,引入韌性理論重新認識北極航行風險,并依托模糊認知圖模型深度分析安全風險的級聯效應。

1 韌性及韌性視域下北極航行風險認知

1.1 韌性理論及其釋義

正如“韌性”釋義為跳回的動作,韌性最早被認知是在工程領域并用來解釋木材受驟然壓力不會斷裂的現象。Holling[7]將韌性理論引入生態學并對“生態韌性”的概念做了反復修正,認為韌性屬于系統自身特性并決定著系統內部關聯的持續性,系統韌性測度以其維持穩態所吸收的擾動量級來計算;隨后在 Holling 的研究基礎上,Berkes 和Folke[8]Gunderson[9]拓展了生態韌性概念,致力于探索“社會-生態系統”中的韌性思維,重點關注了系統穩態變化;Carpenter 等[10]在此基礎上細化了擾動量的具體內涵,將其歸結于吸收的擾動量自組織與學習適應程度。隨著對系統結構機制運行認識的深入,一種源于適應循環理論的演進韌性概念被提出,Folke 等[11]重點強調了持續韌性適應性轉變性,可見演進韌性更關注持續適應并在優化中實現狀態恢復的能力。概而言之,作為研究和分析負面事件的新視域,韌性摒棄了傳統風險管理規避風險或“亡羊補牢”的消極姿態,從系統自身角度出發,將負面事件內化為穩定狀態下的一部分,即為一種“共存”思維。借助“共存”思維所構建的安全邏輯,承認容許并主動應對負面事件。這種安全邏輯普遍被認為應包含吸收適應及變革三個維度[12-15],見表1。因此,總體來看,韌性是系統維持或恢復動態穩定狀態的內在能力,保證系統在面對擾動后能夠繼續運行,以“吸收能力”“適應能力”和“變革能力”為具體表現形式。

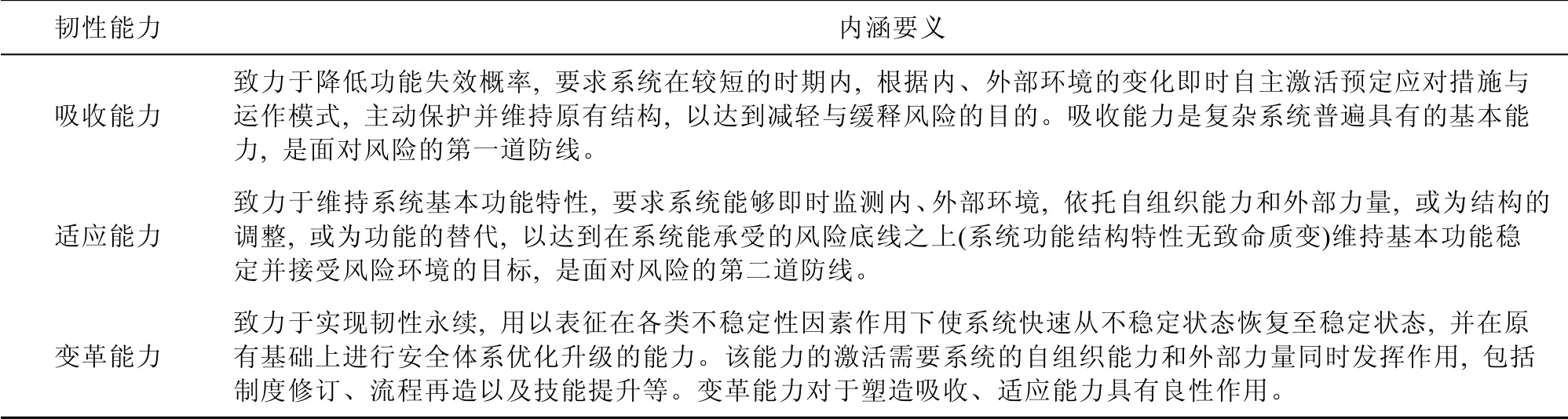
表1 韌性能力的內涵要義Table 1.The connotation of resilience

1.2 韌性視域下的風險及北極航行風險的韌性認知

韌性理論繼承了傳統風險管理與脆弱性研究的優勢,從系統角度出發探討“安全”與“風險”的內在邏輯。Crichton[16]認為風險作為發生損失的概率,應從三方面界定,即危險源脆弱性和暴露度,其中“危險源”指環境中本當存在的風險,“脆弱性”與“暴露度”則決定了系統會不會受到干擾。與其類似,作為韌性理論研究的集大成者,Hollnagel[17]強調了外力在系統韌性建構中引發的負面作用,而這種外力通常源于環境,Hollnagel 的“外力”與Crichton 的“危險源”不謀而合,共同探討了環境中本當存在的風險造成系統能力變化的關鍵作用。但不同的是,Hollnagel 等[18]認為“系統面臨的風險并不是失效概率造成的,而是系統自身功能變化引發擾動的后果”。這一觀點突破了傳統脆弱性視角下的風險定義,將風險發生的原因歸結于系統自身的功能可變性,從系統能力角度出發探尋“韌性能力”與“安全風險”的內在邏輯。“在擾動前后有效調整系統功能可以維護系統韌性”[19],在Hollnagel 等看來,擾動是造成系統韌性發生變化的關鍵因素,控制擾動應以調整系統功能為前提。根據前文可知,擾動來源于系統自身的功能變化,因此,若要達到韌性永續,需要從系統功能可變性角度出發反觀“風險”,即若要維持系統韌性,需要控制哪些擾動,那么“韌性視域下的風險”便應運而生。然而,擾動并不會“憑空出現”,根據前文可知,外力是系統韌性變化的源頭,因此,將“本質性風險”納入“韌性視域下的風險”范疇。同時,將以本質性風險作用于系統自身引發系統功能變化所形成的擾動視作“誘致性風險”。“本質性風險”與“誘致性風險”共同構成“韌性視域下的風險”內涵,見圖1。根據上節對韌性能力的分析,將“誘致性風險”具體分為常規性風險變例性風險與宏觀性風險,以此構建新的研究范式,來認識北極航行安全風險,見表2。

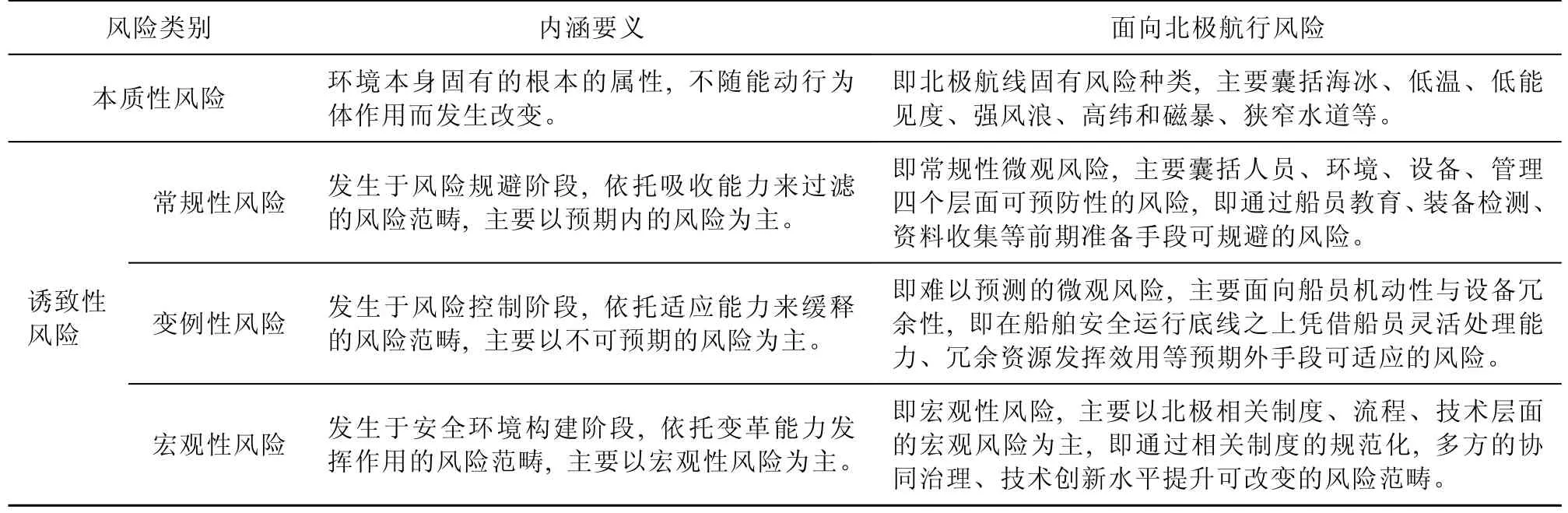
表2 韌性視域下的風險及北極航行風險的韌性認知Table 2.Risks under the resilience perspective and the resilience perception of Arctic navigation risks

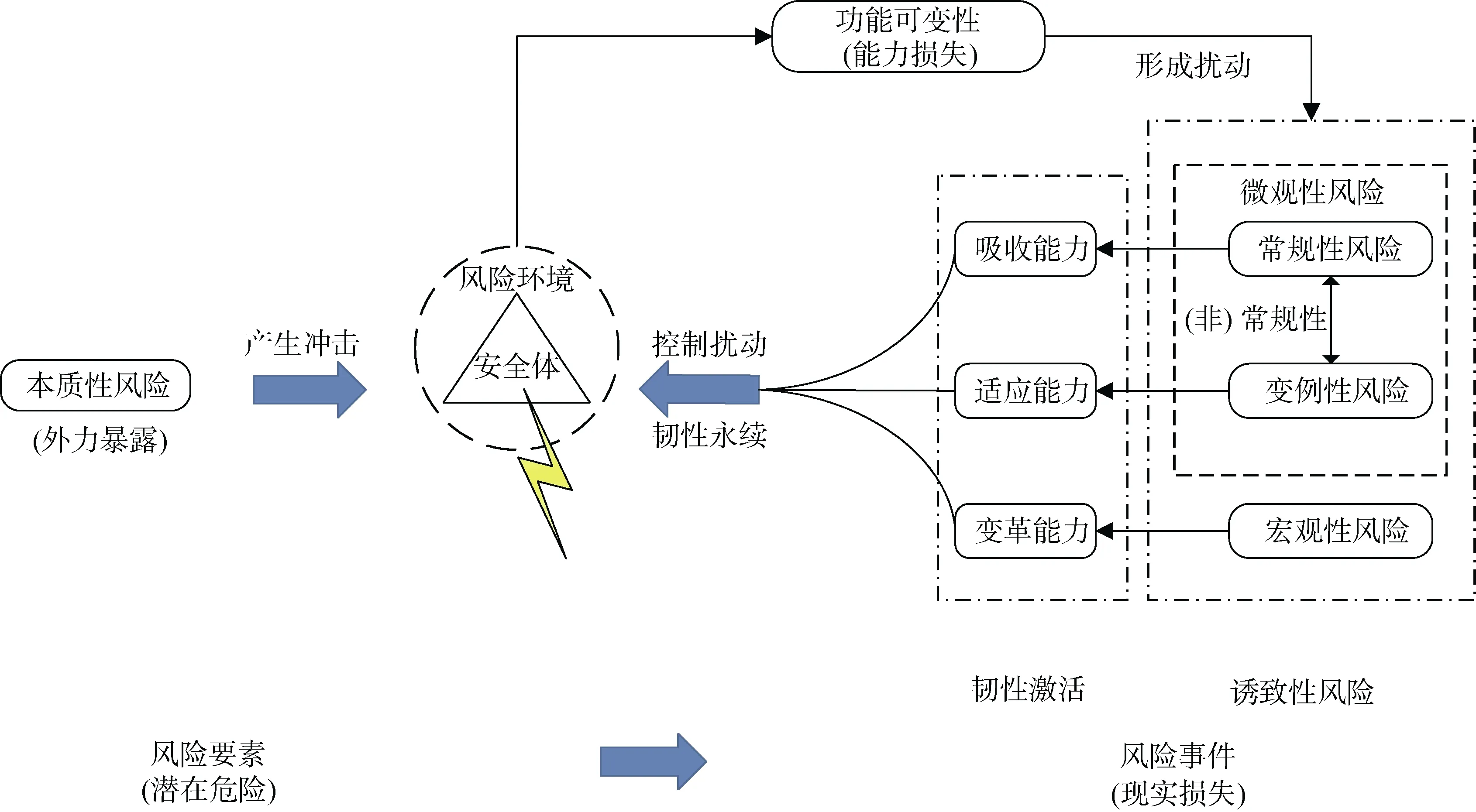
圖1 韌性視域下的風險分析邏輯Fig.1.Risk analysis logic from the perspective of resilience

一般情況下,風險通常被認為是一種潛在的危險,而風險事件的發生使潛在的危險轉化成為現實的損失[20]。從這個意義上來說,當風險尚未對系統安全產生沖擊效果,即風險處于暴露狀態時,風險表現為潛在“風險要素”;當風險對系統產生沖擊效果,即風險處于沖擊狀態時,風險表現為“風險事件”(或稱“風險事故”)。以潛在危險與現實損失劃分“風險要素”與“風險事件”不僅有助于從可變及動態角度掌握風險內涵,更適應了“韌性視域下風險”以及“風險級聯效應”的分析要求。

根據表2,確定韌性視域下北極航行風險的典型風險要素(見表3)。

表3 韌性視域下北極航行安全風險要素Table 3.Arctic navigation safety risk indicators under the resilience perspective

長期以來,針對風險管控問題,研究思路基本是基于“人-機-環-管”四個維度,依托“風險識別-風險評價-風險控制”三個環節構建分析模型,以實現風險規避或控制為最終目標[36-37]。與其不同,韌性理論以肯定并接受環境的非安全性和持續變化為前提,將風險管控視角從外部轉向對研究對象本身功能可變性的剖析。作為一種新探索,“韌性視域下的風險”正是建立在對功能可變性剖析的基礎之上。將“韌性視域下的風險”引入北極航行風險研究,其創新與優勢主要體現為以下幾點。

(1)傳統風險管理研究視角是“由外而內”的,“韌性視域下的風險”是“由內而外”的。這種思維摒棄以外部風險的不確定性為起點對風險問題進行剖析的方式,將研究對象轉向北極安全主體自身,實現從“不可控”到“可控”。

(2)傳統風險管理研究的最終目標是“風險控制”,“韌性視域下的風險”是“風險適應”。“防不勝防”反映了復雜社會環境下應對風險威脅的被動困境,尤其是在北極這個具有高度不確定性與未知性的研究領域下,傳統風險管理模式更是“捉襟見肘”。與傳統風險管理模式不同,“韌性視域下的風險”淡化了“風險防御”概念,承認并主張與未知性共存,以追求安全永續,更適用于探討復雜模糊的北極風險問題。

(3)傳統風險管理研究應對風險威脅是“消極被動”的,“韌性視域下的風險”是“積極主動”的。“識別-評價-控制”從側面反映出風險管理過程的滯后性。類似于病毒變異,北極風險也是持續動態變化的,當我們在識別風險時,風險或早已產生威脅。與其不同,“韌性視域下的風險”從系統自身出發,將風險視為內生產物和功能的邏輯體現了風險管理的態度轉向,更利于我們直面北極風險問題。

2 風險級聯效應及北極航行風險級聯效應的認識

2.1 風險因果關系:風險級聯效應的邏輯起點

逆境下的風險并不固定,而是動態變化的,如果忽視風險間的關聯性往往會導致風險認知偏差[38]。正如前文所述,韌性理論強調對持續穩定狀態的追求,而風險又如此復雜,因此對風險的分析,僅做到認識風險遠遠不夠,有必要準確把握風險間的關系,以保證系統能夠實現韌性的永續。

風險級聯效應常被簡單認為是多米諾骨牌效應,但這顯然是不準確也不嚴謹的。作為理解風險社會的重要視角,“級聯”及“級聯效應”受到供應鏈風險管理災難管理運營風險管理等多個研究領域的關注,但“級聯效應”在不同的應用場景中,其概念并不固定。在供應鏈風險管理中,更傾向于以“風險傳播”來定義風險級聯效應,將其界定為供應鏈網絡中某個節點發生故障,進而產生連鎖反應,放大風險破壞效果的過程[39-40]。在災難管理領域,Caroleo 等[41]將級聯效應定義為特定隱患發生所可能導致的事件鏈。雖然學界目前對“級聯效應”的描述并不一致,但是通過文獻梳理發現,目前有關風險級聯效應的研究多從風險要素間的因果關系出發來討論級聯過程,Feng 等[42]則借助貝葉斯網絡分析定義風險要素及其因果關系,以此為基礎探討風險級聯過程的復雜性和不確定性。與之類似,Fang 和Marle[43]開發了決策支持系統框架,構建的網絡結構將“節點”視作風險,“邊”視作因果關系,以此展開模擬,闡釋了忽略項目風險的級聯效應會導致決策過程失誤的觀點。

綜合來看,風險間存在著普遍的因果關系,它既是引發風險級聯效應的源頭[44],也是主要驅動因素。作為“導火索”,風險“因果關系”與“級聯”“級聯效應”存在著復雜的聯系。具體來看,當多個風險要素均未產生擾動效果時,它們之間普遍存在潛在的因果關系,這種關系是靜態的,不會對系統安全產生影響。所謂“級聯”是指當某個風險要素產生沖擊效果后,該要素與其他風險要素間的因果關系便活躍起來,進而激活其他風險要素,形成“風險事件”的過程。所謂風險“級聯效應”是指在風險“級聯”的基礎之上,多個風險要素共同產生沖擊效果,驅動因果關系,促成二次甚至更多次級聯,形成復雜風險事件鏈的動態過程。可以說風險“因果關系”是“級聯效應”的本質和內生動力,“級聯效應”是“因果關系”的外在表現形式,而風險由潛在“風險要素”激活為“風險事件”的過程便是促成“因果關系”轉變為“級聯效應”的催化劑。

2.2 北極航行風險因果關系

根據級聯效應理論分析可知,探討風險要素之間的因果關系是展開級聯效應分析的第一步。因此,依據相關文獻資料事故報告及專家意見收集來確定二級指標間的因果關系,見表4。在獲取風險要素因果關系后,以此為基礎展開北極航行風險級聯效應分析。

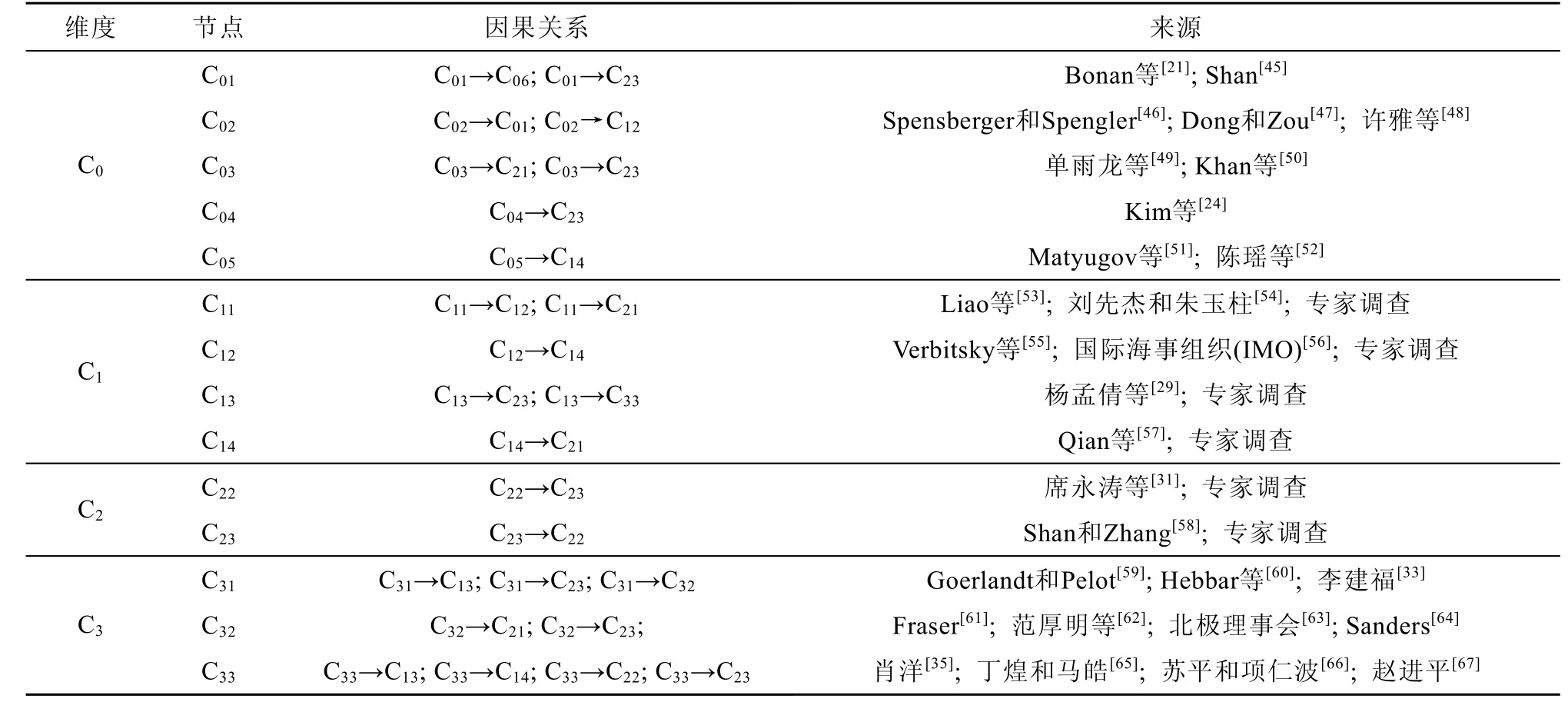
表4 北極航行風險要素因果關系說明及來源Table 4.The causal relationship between the secondary indicators and the references

3 因果知識表示的FCM 分析法

3.1 模糊認知圖分析法:表示與推理

Aexlord 首次提出了一種由概念節點有向弧及關聯權重三元素所構成的認知圖模型并將其應用于商業或制度決策的過程。其中,概念節點代表事件,有向弧表示兩者間的因果關系,權重則代表兩者間的關聯效果。而后Kosko[68]在Aexlord的基礎上改進了離散的關聯效果并確定了[-1,1]的關聯強度區間以適應于模糊推理,模糊認知圖(Fuzzy Cognitive Map,FCM)模型應運而生。

(1)FCM 的結構表示

FCM 將模糊理論與網絡結構結合。基本圖解結構由概念節點和有向弧組成,所有概念節點間的聯系及相互作用組成了一個動態系統。圖2 即為一個簡單的FCM 模型,具有5 個概念節點(C1C2C3C4C5),其中C1對C2存在有向弧,含義為概念節點C1狀態值的改變會導致概念節點C2狀態值的改變,其關聯程度為有向弧權值w12,其余5 條有向弧也具備相似的含義。由圖解結構模型可得FCM 鄰接矩陣。

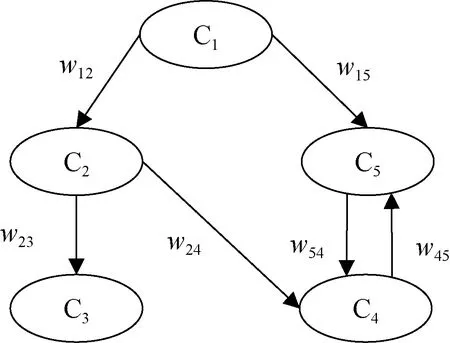
圖2 模糊認知圖結構示意圖Fig.2.Schematic diagram of FCM structure

(2)FCM 的數學表示與推理機制

FCM 基本模型以簡單的四元組G=(C,X,W,f)進行數學表示,其中,由n個概念節點組成的集合C={C1,C2,…,Cn};概念節點C1至Cn在某一時刻的狀態值組成的集合X={x1,x2,…,xn};任意兩個概念節點Ci對Cj的有向弧權值所構成的集合W={wij},則W={wij}n×n即為整個FCM 模型的鄰接矩陣;f代表閾值函數,其目的是將每次迭代后的節點狀態值轉化為[-1,1]。每個節點在不同時間點的狀態值不同,若在時間點t時,n個概念節點組成的狀態值集合X(t)={x1(t),x2(t),…,xn(t)},那么在時間點t+1 時,n個概念節點的狀態值即為:

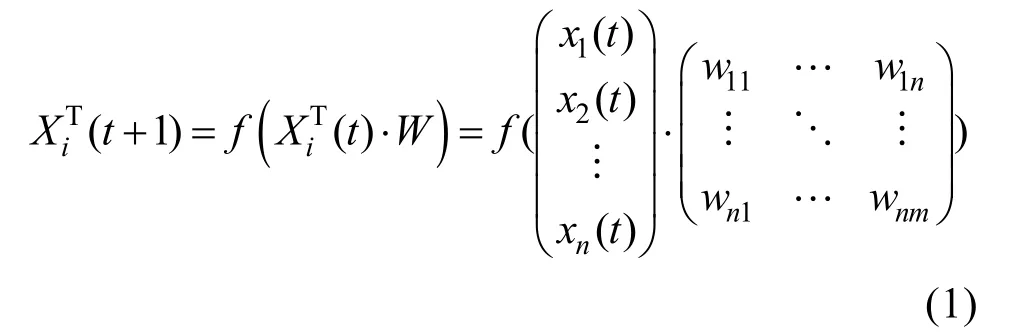
常見的閾值函數有雙曲正切函數,Sigmoid 函數。根據模糊特征,選擇陡度參數λ的Sigmoid函數為閾值函數:

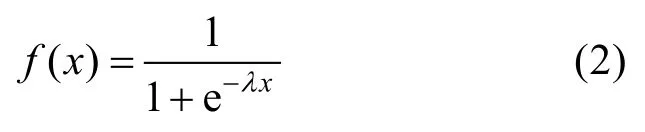
對概念節點的狀態值進行迭代計算后,將最終穩定至一個固定點或極限循環兩種狀態。但實際上,FCM 推理也可能會使各個節點進入無限不循環狀態,即為一種混沌狀態。

3.2 模糊認知圖分析法有向弧權值:模糊層次分析法

FCM 因果關系形成后,對存在因果關系的兩個概念節點間的有向弧權重做進一步分析。文章引入梯形模糊數法及專家置信度水平來進行模糊綜合評估[69]。首先收集并量化專家評語。邀請海上交通安全領域北極安全領域內共5 位專家并展開問卷調查,將調查結果轉化為梯形模糊數A=(a1,a2,a3,a4)(表5)。其次,計算專家置信度。受異質專家的個人閱歷知識背景行業經驗的影響,專家評語往往不可一概而論。引入專家置信度(專家權重)概念,從職位水平(epl)學歷水平(edl)經驗水平(eel)和適任水平(ecl)來確定專家綜合置信程度,評分標準見表6。專家評語置信度(el)以及專家置信度Q(Eu)的計算公式分別為:

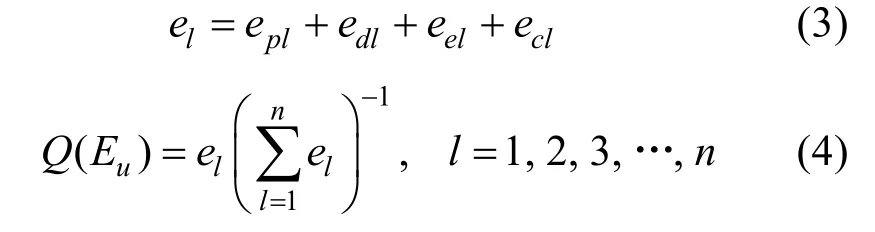
表5 專家評語標度Table 5.Expert comment scale

表6 專家置信度評分標準Table 6.Expert confidence scoring standards

第m位專家評語為Pm(m=1,2,…,n),分別計算專家評語的平均一致度和一致性系數并進行去模糊化處理,測量有向弧權重。

第1 步,評語間相似度計算:若以Pu(a1,a2,a3,a4)和Pv(b1,b2,b3,b4)表示兩位專家評語的梯形模糊數標度,那么兩位專家間評語相似度Suv(Pu,Pv)表示為:

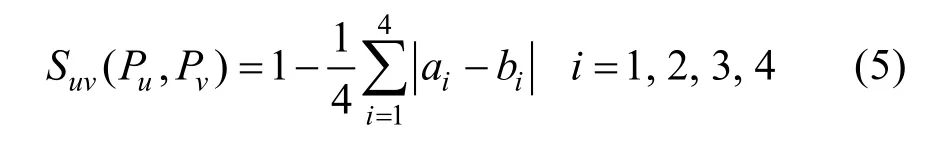
第2 步,平均一致度計算:若有n位專家,第u位專家評語平均一致度AA(Pu)表示為:

第3 步,相對一致度計算:若有n位專家,第u位專家評語相對一致度RA(Pu)表示為:

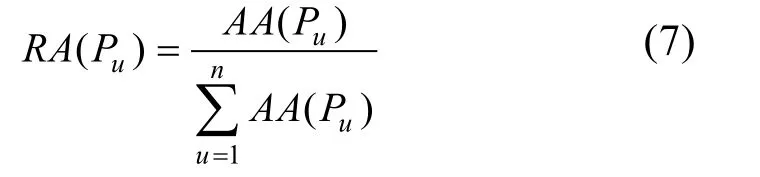
第4 步,一致性系數計算:Q(Eu)對于RA(Pu)的重要程度以β表示,β取0.5,第u位專家的一致性系數CC(Pu)表示為:

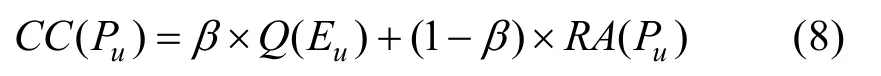
第5 步,聚類模糊數計算:聚類模糊數以RA表示為:

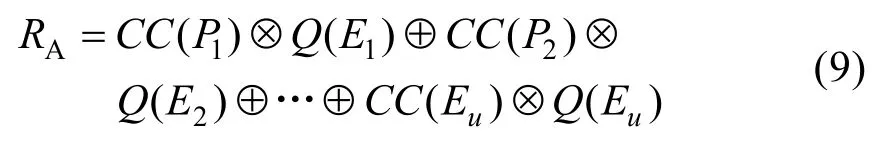
第6 步,去模糊化處理:采用中心面積法去模糊化,以μM(x)表示聚合的隸屬函數,去模糊化權重以AV表示為:

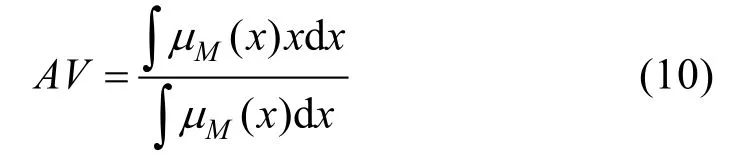
當模糊綜合評價集采用梯形模糊數標度時,若梯形模糊數為A=(a1,a2,a3,a4),則有:

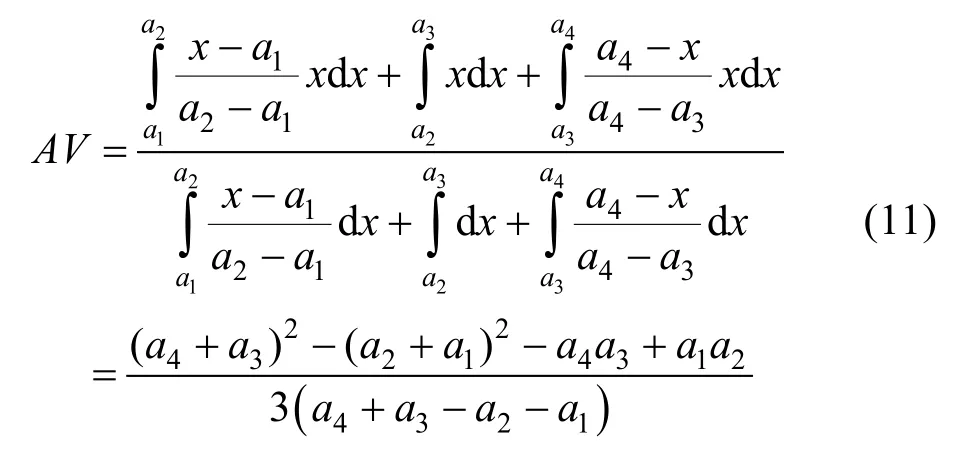
4 韌性視域下北極航行風險級聯效應分析

4.1 風險指標判斷標準與情景選定

根據前文分析可知,風險存在兩種表現形式,當風險狀態未達到既定閾值時,風險僅可被視作具有潛在危險性的“風險要素”;當風險達到甚至超過既定閾值時,風險由潛在危險狀態轉變為具有現實損失的破壞性“風險事件”。因此,確定閾值以判斷風險表現至關重要。在綜合國內外北極航線風險等級界定標準以及廣泛征詢專家意見的基礎上,結合前期研究成果以及研究區域背景狀況,針對定量客觀指標,即本質性風險,構建判斷層來界定風險要素及其量值范圍(表7)。對于定性指標,即誘致性風險,由于指標自身具有一定的籠統性和不確定性,很難以統一的標準來界定其量值范圍,因此誘致性風險量值范圍主要通過領域內專家和具有北極航行經驗船員的打分結果獲得。表7 為獲取北極航行風險因果關系強度以及級聯效應情景模擬分析提供了重要的指示性參考。

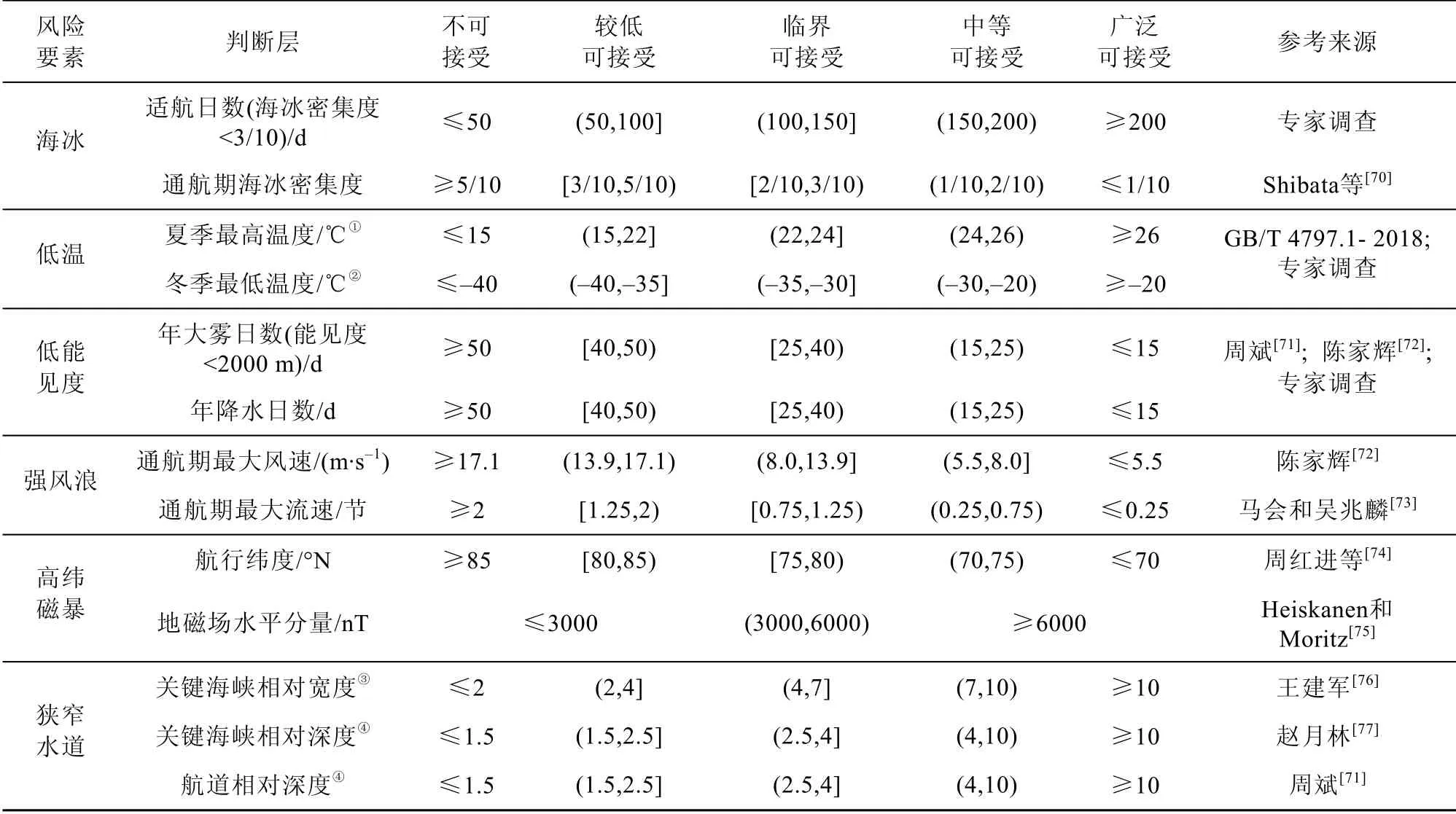
表7 北極航行本質性安全風險指標判斷標準及參考來源Table 7.Judgement standards for essential risk of Arctic navigation and reference sources

通過文獻分析與專家意見收集,確定當風險節點中的任意一個判斷層指標達到“較低可接受”水平時,風險節點便處于激活狀態。處于激活狀態的風險節點具備兩種能力,一是能夠對系統產生干擾,二是能夠促使與其相關的因果關系鏈活躍起來,進而產生風險級聯。從北極客觀環境出發,以表8 收集到的事故報告分析為基礎,將“海冰”“低溫”兩個本質性風險確定為北極航行常態化風險要素,將“船員適任性低”及“國際交流渠道狹窄”兩個誘致性風險確定為高頻風險要素。以此為例分別開展本質性風險級聯效應情景分析以及誘致性風險級聯效應情景分析。

表8 底層數據統計信息及其來源Table 8.The underlying data statistics and their sources

4.2 北極航行風險FCM 模型構建

根據表4 北極航行風險因果關系,構建由一級指標間一級與二級指標間以及二級指標間的聯合模糊認知圖模型(圖3)。

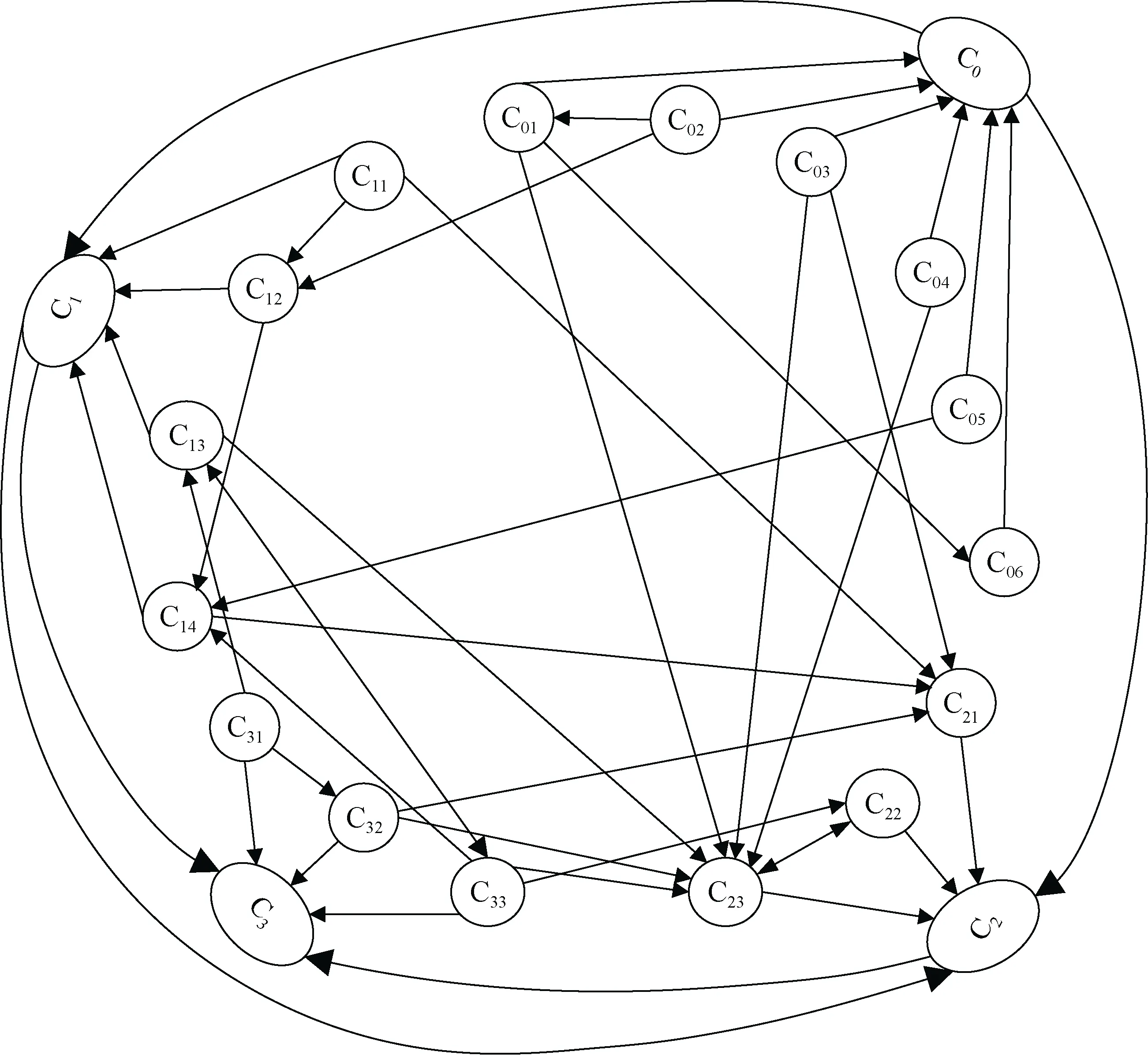
圖3 韌性視域下北極航行風險的模糊認知圖Fig.3.A fuzzy cognition map of Arctic navigation risks from the perspective of resilience

4.3 北極航行風險因果關聯程度分析

為保證研究結果科學可靠,以表7 和表8 為指示性參考,選擇北極安全海上交通安全領域內的科研專家和有經驗的船員組成異質專家組展開討論與調查。根據表6 及公式(3)(4)對每位專家的置信度進行計算,專家信息及置信度水平見表9。

表9 專家信息及置信度水平Table 9.Expert information and the confidence level

根據公式(5)～(11)計算存在因果關系的有向弧權值,三類因果關系的有向弧權值測量結果見表10。

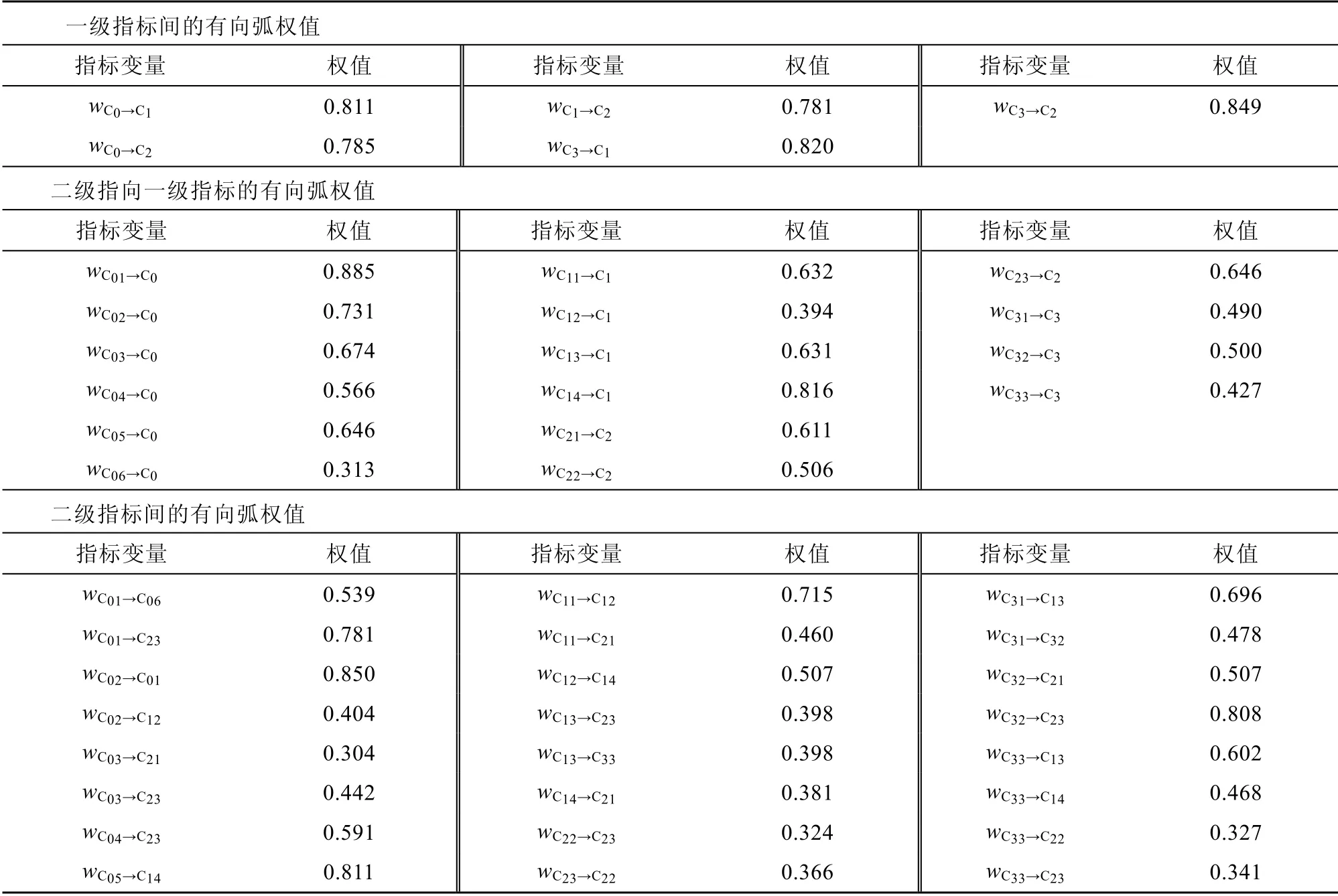
表10 FCM 有向弧權值Table 10.FCM directed arc weights

本研究共確定了45 條有向弧權值,其中,一級指標間,C3→C2的因果關系最強,有向弧權值達到0.849;C3→C1的因果關系次之,有向弧權值達到0.820,表明在一般情況下,“宏觀性風險”對導致“常規性風險”與“變例性風險”具有很強的效果。一級與二級指標間,C01→C0的因果關系最強,有向弧權值達到0.885,表明在一般情況下“海冰”對導致“本質性風險”水平的提高具有很強的效果;C14→C1的因果關系次之,有向弧權值為0.816,表明在一般情況下,“導助航設備失靈”對導致“常規性風險”水平的提高具有很強的效果。二級指標間,C02→C01的因果關系最強,有向弧權值達到0.850,表明在一般情況下“低溫”對導致“海冰”具有很強的效果,C05→C14的因果關系次之,有向弧權值為0.811,表明在一般情況下“高緯和磁暴”對導致“導助航設備失靈”具有很強的效果。

4.4 情景一:北極航行本質性風險的級聯效應分析

激活模糊認知圖中特定節點開展情景模擬分析。激活特定風險節點后,經過多次迭代,如果模型中其他風險節點的狀態值不再發生明顯變化,符合收斂性要求,則表明該情景具有現實意義,此時,所有節點的最終狀態值與初始狀態值之間的差值表征該節點與激活風險節點之間的級聯強弱[80]。如果多次迭代后,其他風險節點狀態值無法收斂,表明激活的風險節點與其他任何風險節點間不存在明顯的級聯關系。以本質性風險中的“海冰C01”和“低溫C02”作激活風險節點為例,風險的級聯效應分析過程為:

(1)第一階段:以C01C02為激活節點

第1 步,定義初始向量,賦予初始向量狀態值:20 個概念節點組成的初始狀態值集合X(0)={1,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0}。

第2 步,遞推下一時刻狀態值,迭代狀態值:根據公式(1)得出下一時刻狀態值。

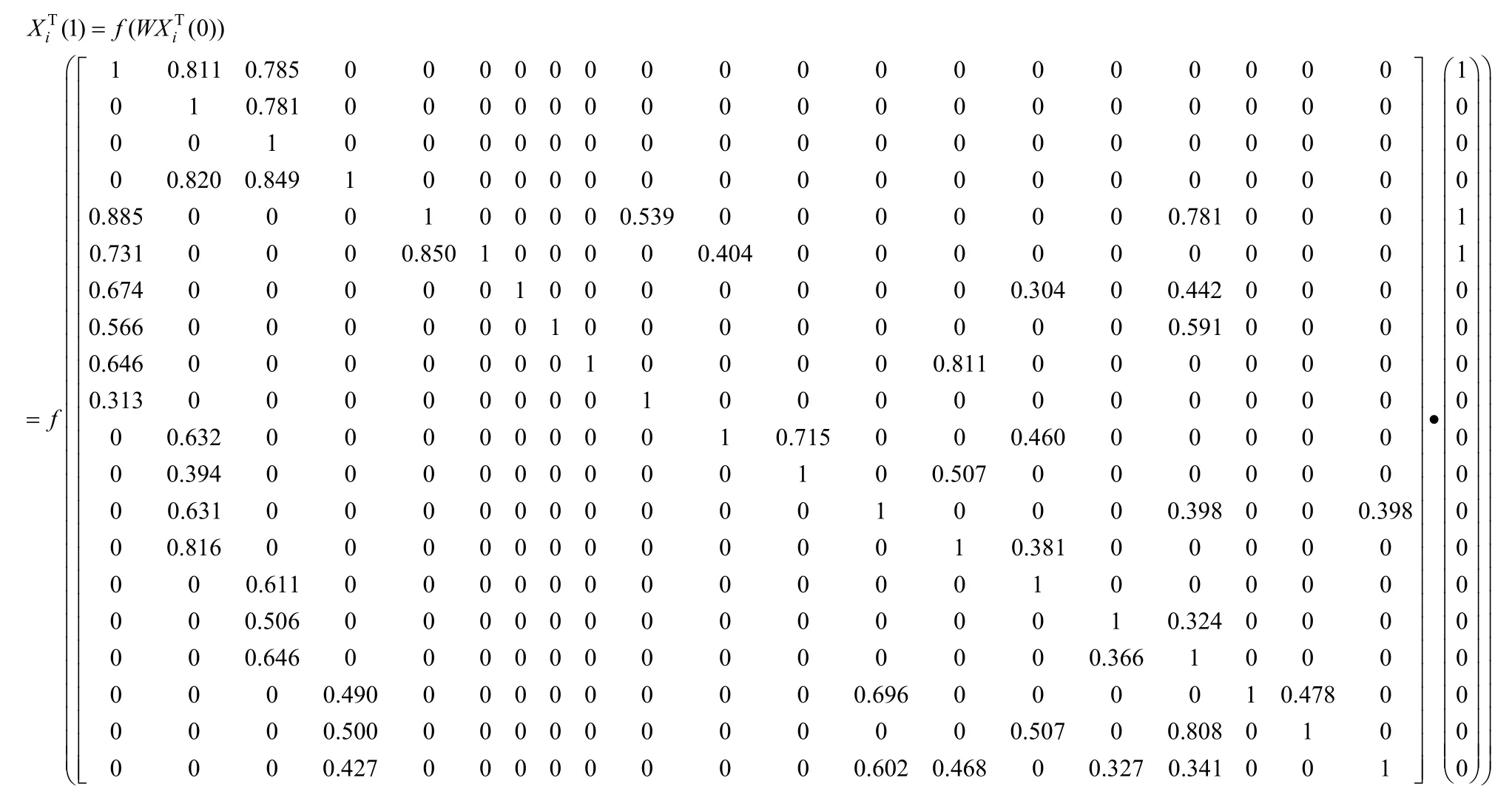
根據公式(2)代入變換函數,其中λ取5,則有:

第3 步,校準狀態向量:滿足X(t)=X(t+ 1),則迭代結束,X(t+ 1)為最終狀態向量值。顯然X(1)≠X(0),即X(1)不是模型最終狀態向量值,需要繼續迭代計算。

第4 步,多次迭代直至狀態值穩定:在本情境下,經過13 次迭代計算,得到X(12)=X(13),即X(13)為最終狀態向量值。部分迭代次數狀態向量值及數值變化幅度M(Ci)如表11所示,其中Is表示第s次迭代。

表11 部分時刻各節點狀態向量值及數值變化幅度(情景一:第一階段)Table 11.The state vector value and numerical change range of each node at some time(scenario 1:first stage)

在推理的過程中,激活節點以外的其他節點狀態值均發生了變化,表明其他風險節點均與“海冰”和“低溫”存在一定的級聯關系。M(Ci)表示第i個節點初始狀態值與收斂狀態值之間的差值,數值越小,表明該節點與激活風險節點的級聯性越強。按照M(Ci)由小到大依次是“獲援概率極低C23”(0.0197)“狹窄水道C06”(0.0629)“維護保養不到位 C12”(0.1173),其他節點的M(Ci)均在0.49 附近,這說明在“海冰”“低溫”風險環境下,最容易導致的風險事件依次是“獲援概率極低”“狹窄水道”“維護保養不到位”。那么在下一階段的情景模擬過程中,激活節點便由2 個擴大到5 個。

(2)第二階段:以C01C02C06C12C23為激活節點

以“海冰”“低溫”“狹窄水道”“維護保養不到位”“獲援概率極低”驅動模糊認知圖模型,重復第一階段的第1～4 步,觀察M(Ci),結果如表12所示。

根據表12,經過第二階段的推理發現,以源激活節點(“海冰”“低溫”)及一次級聯節點(“維護保養不到位”“獲援概率極低”“狹窄水道”)為新的激活節點驅動模糊認知圖模型,除了一次級聯節點M(Ci)較第一階段明顯變小以外,按照M(Ci)由小到大依次是“導助航設備失靈 C14”(0.0733)“設備搶修速度慢C22”(0.1379),其他節點M(Ci)均在0.49 附近。這說明在該情景下,當風險事件遞進至第二階段時,最容易導致的風險事件依次是“導助航設備失靈”“設備搶修速度慢”。

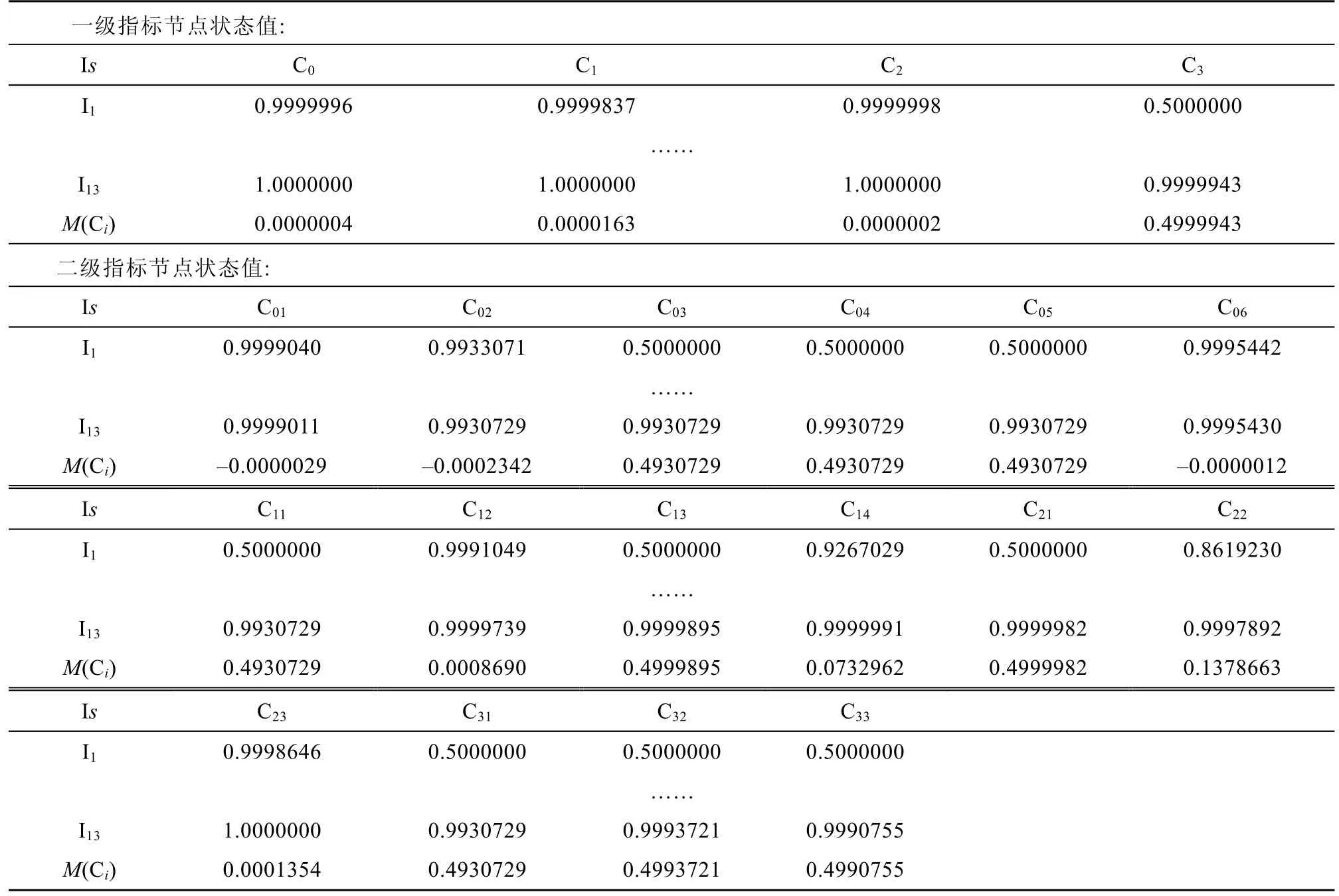
表12 部分時刻各節點狀態向量值及數值變化幅度(情景一:第二階段)Table 12.The state vector value and numerical change range of each node at some time(scenario 1:second stage)

(3)第三階段:以C01C02C06C12C14C22C23為激活節點

以“海冰”“低溫”“狹窄水道”“維護保養不到位”“導助航設備失靈”“設備搶修速度慢”“獲援概率極低”驅動模糊認知圖模型,重復第一階段的第1～4 步,觀察M(Ci),結果如表13所示。

根據表13,經過第三階段的推理發現,以源激活節點(“海冰”“低溫”)一次級聯節點(“維護保養不到位”“獲援概率極低”“狹窄水道”)及二次級聯節點(“導助航設備失靈”“設備搶修速度慢”)為新的激活節點驅動模糊認知圖模型,除了二次級聯節點M(Ci)較第一階段明顯變小以外,只有“疏散調度能力弱C21”對應的M(Ci)明顯變小,為0.1296。這說明在該情景下,當風險事件遞進至第三階段,最容易導致的風險事件是“疏散調度能力弱”。

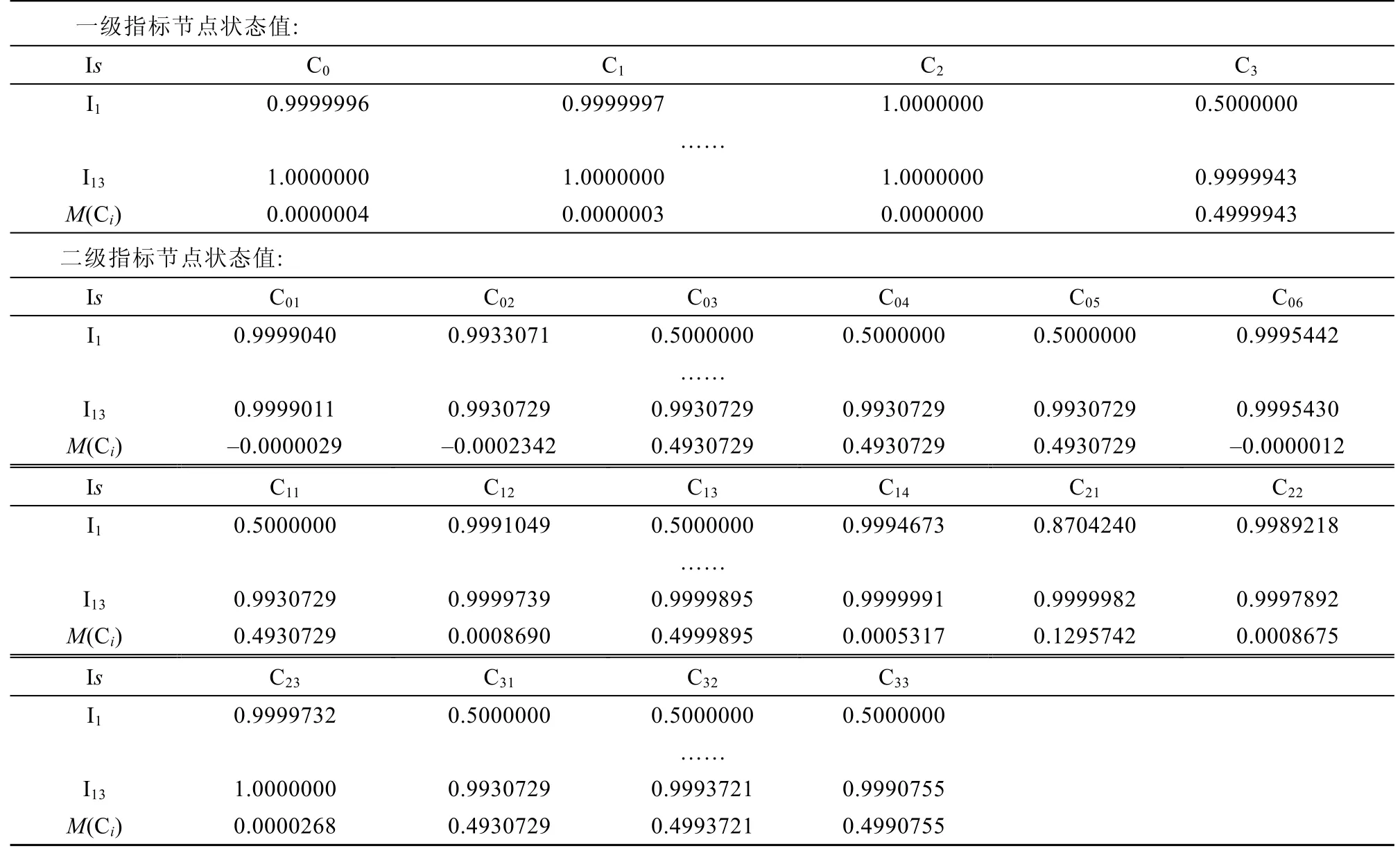
表13 部分時刻各節點狀態向量值及數值變化幅度(情景一:第三階段)Table 13.The state vector value and numerical change range of each node at some time(scenario 1:third stage)

(4)第四階段:以C01C02C06C12C14C21C22C23為激活節點

以“海冰”“低溫”“狹窄水道”“維護保養不到位”“導助航設備失靈”“疏散調度能力弱”“設備搶修速度慢”“獲援概率極低”驅動模糊認知圖模型,重復第一階段的第1～4 步,觀察M(Ci),結果如表14所示。

根據表 14,經過第四階段的推理發現,以源激活節點(“海冰”“低溫”)一次級聯節點(“維護保養不到位”“獲援概率極低”“狹窄水道”)二次級聯節點(“導助航設備失靈”“設備搶修速度慢”)及三次級聯節點(“疏散調度能力弱”)為新的激活節點驅動模糊認知圖模型,除了三次級聯節點的M(Ci)較第二階段明顯變小以外,其余節點M(Ci)均沒有發現明顯的變化,即沒有導致新的風險發生。則以“海冰”“低溫”為源激活節點的風險級聯過程情景模擬結束。

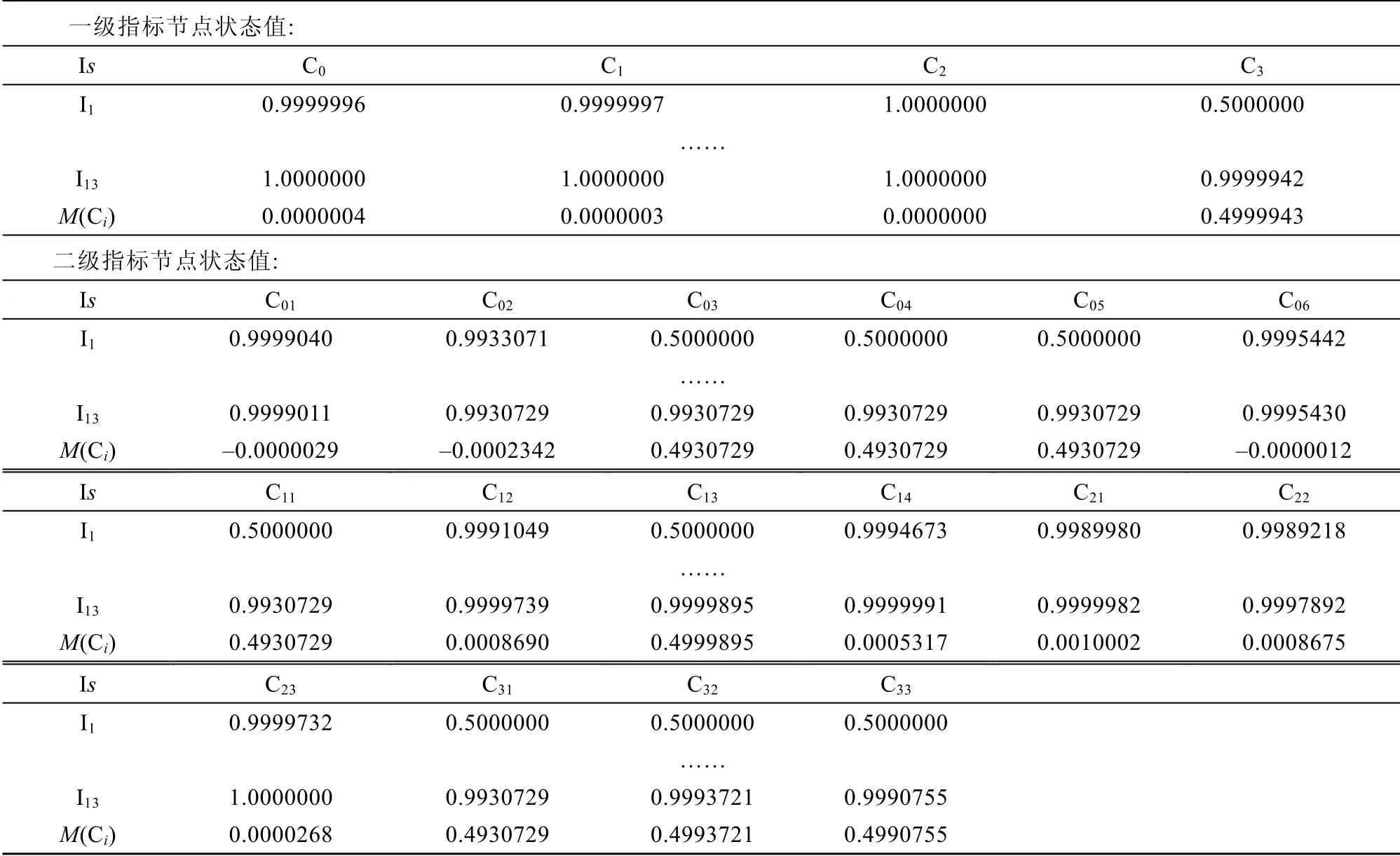
表14 部分時刻各節點狀態向量值及數值變化幅度(情景一:第四階段)Table 14.The state vector value and numerical change range of each node at some time(scenario 1:fourth stage)

4.5 情景二:北極航行誘致性風險的級聯效應分析

“海冰C01”與“低溫C02”是北極航行常態化風險要素,在分析誘致性風險級聯效應過程中也應處于激活狀態。在分析表8 中相關事故報告

的基礎上,選取“船員適任性低C11”“國際交流渠道狹窄C31”兩個誘致性風險要素作為激活節點,開展風險級聯效應分析工作,計算過程同第4.4 節。

(1)第一階段:以C01C02C11C31為激活節點

以“海冰”“低溫”“船員適任性低”“國際交流渠道狹窄”為激活節點驅動模糊認知圖模型,重復4.4 節的第1～4 步,觀察M(Ci),結果如表15所示。

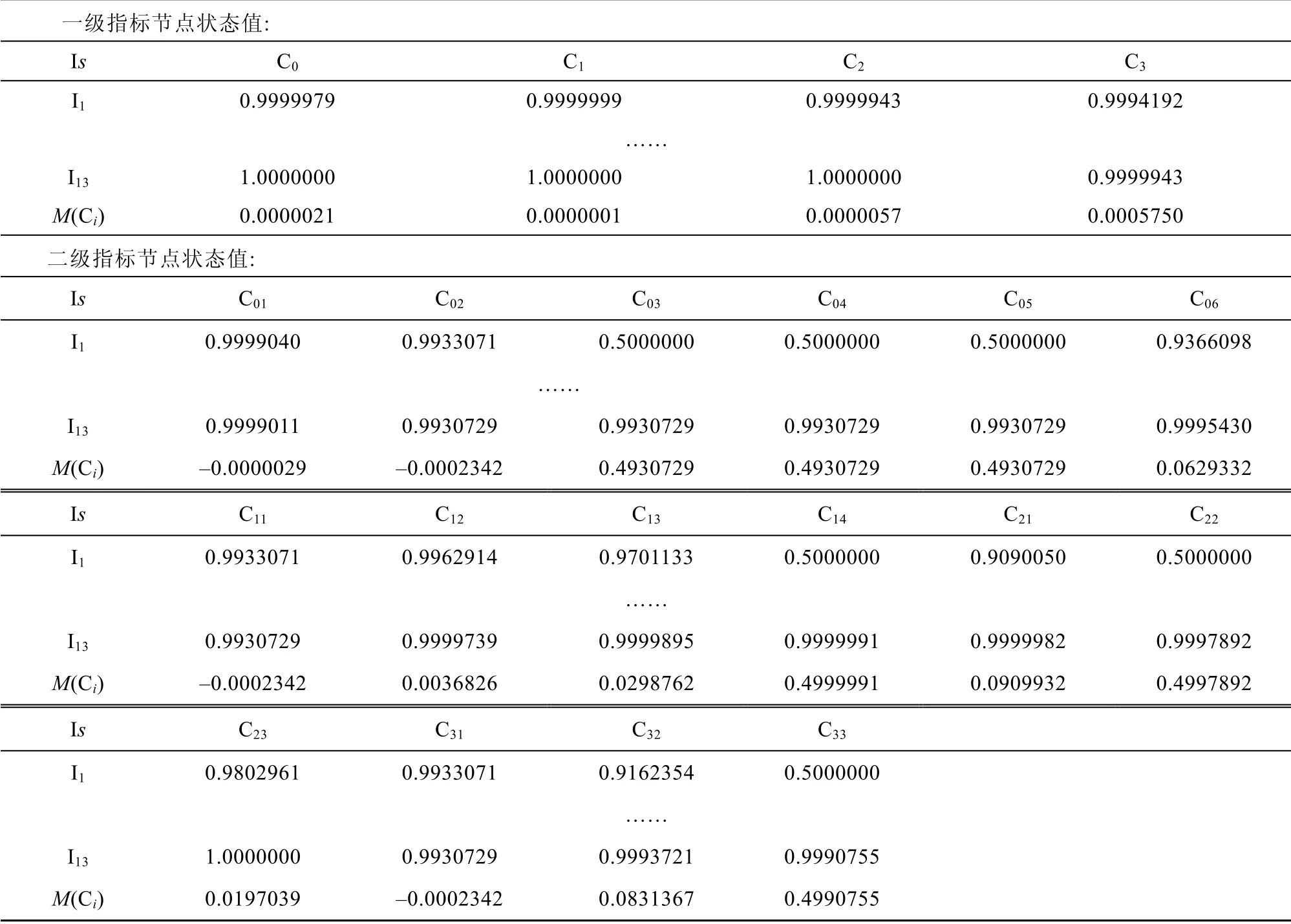
表15 部分時刻各節點狀態向量值及數值變化幅度(情景二:第一階段)Table 15.The state vector value and numerical change range of each node at some time(scenario 2:first stage)

根據表15,經過第一階段的推理發現,每個風險節點的狀態值均有所不同,表明以C01C02C11C31為激活風險驅動模糊認知圖展開情景模擬具有現實意義。按照M(Ci)由小到大依次是“維護保養不到位C12”(0.0037)“獲援概率極低C23”(0.0197)“北極航行資料缺失C13”(0.0299)“狹窄水道C06”(0.0629)“北極救援力量匱乏C32”(0.0831)及“疏散調度能力弱C21”(0.0910),其他節點M(Ci)均在0.49 附近。這說明在常態化風險環境下(海冰和低溫),“船員適任性低”以及“國際交流渠道狹窄”形成的風險組合最容易導致的風險事件依次是“維護保養不到位”“獲援概率極低”“北極航行資料缺失”“狹窄水道”“北極救援力量匱乏”及“疏散調度能力弱”。

(2)第二階段:以C01C02C06C11C12C13C21C23C31C32為激活節點

以“海冰”“低溫”“狹窄水道”“船員適任性低”“維護保養不到位”“北極航行資料缺失”“疏散調度能力弱”“獲援概率極低”“國際交流渠道狹窄”“北極救援力量匱乏”為激活節點驅動模糊認知圖模型,重復4.4 節中第1～4步,觀察M(Ci),結果如表16所示。

表16 部分時刻各節點狀態向量值及數值變化幅度(情景二:第二階段)Table 16.The state vector value and numerical change range of each node at some time(scenario 2:second stage)

根據表16,經過第二階段的推理發現,以源激活節點(“海冰”“低溫”“船員適任性低”“國際交流渠道狹窄”)及一次級聯節點(“維護保養不到位”“獲援概率極低”“北極航行資料缺失”“狹窄水道”“北極救援力量匱乏”及“疏散調度能力弱”)為新的激活節點驅動模糊認知圖模型,除了一次級聯節點的M(Ci)較第一階段明顯變小以外,按照M(Ci)由小到大依次是“導助航設備失靈C14”(0.0733)“科考及技術創新不足C33”(0.1193)“設備搶修速度慢C22”(0.1379)。這說明在該情景下,當風險遞進至第二階段,最容易導致的風險事件依次是“導助航設備失靈”“科考及技術創新不足”“設備搶修速度慢”。同時,可以發現,當風險狀況遞進至該階段時,除了部分本質性風險M(Ci)沒有明顯變化外,其他風險均被激活,表明誘致性風險相對于本質性風險在風險級聯過程中的連鎖效應更迅速也更為猛烈。由于各個節點均被激活,在此情景下,風險級聯效應模擬過程結束。

4.6 結果解析與方法評析

根據模擬過程,做出如下分析。

以“海冰”“低溫”為源激活節點開展北極航行風險級聯效應的情景模擬結果顯示:風險級聯效應共經歷了四個階段,最容易導致“獲援概率極低”“狹窄水道”“維護保養不到位”。整體來看,級聯過程激活的6 個風險節點均對應韌性理論下的吸收和適應能力。因此,未來北極航行安全保障基礎能力建設過程中應重點發展風險的吸收和適應能力。

以“海冰”“低溫”“船員適任性低”“國際交流渠道狹窄”為源激活節點開展北極航行風險級聯效應的情景模擬結果顯示:風險級聯效應共經歷了兩個階段,最容易導致“維護保養不到位”“獲援概率極低”“北極航行資料缺失”。整體來看,級聯過程中,誘致性風險下的全部節點均被激活。因此,在誘致性風險主動發揮作用時,北極航行安全保障基礎能力建設過程中應同時關注風險的吸收適應和變革能力。

北極水域環境復雜多變,脆弱敏感,非傳統性安全風險越來越成為北極航行風險研究的關注重點[31]。從風險識別到風險評價,再到風險控制,北極航行風險管理研究逐步體系化。傳統視角下的北極航行風險要素識別主要集中于兩大方面:一方面,基于“人-機-環-管”的北極航行風險分析成為主流框架[81],其中也有對四大維度中某一要素(如海冰[82]磁場[74]等)的細化研究;另一方面,依托碰撞或擱淺事故展開的風險分析模式也較為常見[27,83]。其次,在分析方法方面,除了有貝葉斯網絡[5]事故樹[84]神經網絡[49]等定量分析模型的引入以外,也有基于理論層面的定性探討[85]。從傳統分析方法取得的結論來看,譬如:有借助加權綜合評價展開北極東北航道風險區劃分析,得出了海冰風速對北極安全航行影響較大的結論[86];有依托模糊層次分析法從經濟技術政治安全幾個角度對北極航道綜合性風險進行排序[87],證明了航行安全和地緣政治領域的風險點對北極航行有重要的影響;同時也有基于“馬爾科夫鏈-蒙特卡洛方法”構建了云模型,得出北極航行風險隨時間變化波動明顯的結論[88]。從研究方法到研究結果,總結來看,依托于傳統風險分析方法所得出的研究結論主要集中于兩個方面,一是能夠識別出北極航行關鍵風險要素,二是證實了風險要素間存在著動態變化過程。所以,將以上兩個研究議題結合起來,深入探討關鍵風險要素之間的互動關聯,模擬(還原)這種動態變化過程,為突破風險困境提出保障能力建設策略顯得更加重要。這是目前國內外學者較少關注的問題。因此,突破現有對于風險要素識別及其自身影響效果分析的研究界限,基于韌性理論,依托模糊認知圖模型,模擬了兩種情景下的風險級聯過程。與現有研究方法取得的結果不同,該方法能夠明晰北極航行風險級聯效應究竟如何放大,明確風險之間的關聯傳遞過程。同時,更為重要的一點是,所采用的“風險-韌性”框架能夠直接從量化結果中明確北極航行安全保障能力建設的著力點,這實際上擺脫了先問題分析,后對策建議,將兩者割裂來看的研究范式,實現了“問題”與“對策”融合,這也恰恰體現了“風險”與“韌性”的內在邏輯與韌性理論研究優勢。

5 結論

北極航行風險具有模糊多變的特征,傳統風險分析范式的研究視角始終困囿于“由外而內”“風險控制”“消極被動”的層面。因此,在現實與技術的矛盾下,應對北極航行風險很難擺脫左支右絀的困境。韌性理論框架下的北極航行風險研究實現了“由內到外”“由‘風險控制’到‘風險適應’”“由‘消極被動’到‘積極主動’”的姿態轉變,即在承認北極航行風險模糊復雜可變敏感的前提下,應該如何從安全主體角度出發來看待和控制北極航行風險。在該理論的指引下展開風險指標識別,將“韌性”與“級聯效應”結合,首次探討了北極航行風險的級聯效應,改變了傳統分析方法集中于北極航行風險的表面性研究,真正將風險串聯起來。另外,將模糊認知圖分析法引入北極航行風險分析中來,為風險理論中的級聯效應研究提供了量化分析路徑。

本研究基于韌性理論的三個能力要素(吸收適應變革)提出了一個以韌性視角來認知北極航行風險(本質性常規性變例性宏觀性)的研究范式,并以此為切入點對北極船舶航行安全風險級聯效應做深入分析。引入梯形模糊數和模糊層次分析法來量化各風險節點間的因果關系強度,構建了可用于韌性視域下北極航行安全風險分析的模糊認知圖,為采取模擬實體方法研究北極航行安全風險提供了通用模型。最后針對兩種風險情景,通過級聯效應分析,模擬風險級聯過程,指出為獲取持續安全狀態所應當重點關注的韌性能力。研究表明:北極常態化風險環境(海冰和低溫)下,風險級聯效應共產生四個階段,最容易導致“獲援概率極低”“狹窄水道”“維護保養不到位”等,此情景下應重點關注風險的吸收和適應能力;在常態化風險環境耦合“船員適任性低”和“國際交流渠道狹窄”兩個誘致性風險的情景下,風險級聯效應共產生兩個階段,最容易導致“維護保養不到位”“獲援概率極低”“北極航行資料缺失”等,此種情景風險級聯效應的過程更為迅速和猛烈,應同時兼顧風險的吸收適應和變革能力。