n-直覺多邊形模糊有序加權距離算子及其在綠色供應商評價中的應用

陳 媛，耿秀麗 （上海理工大學 管理學院，上海 200093）

0 引言

不確定信息的處理是多屬性決策研究中的重要問題。Zadeh在1965年提出模糊集理論并將其用于解決不確定信息。Atanassov為改進傳統模糊集中僅考慮隸屬度的缺陷，提出了直覺模糊集的概念，在單一隸屬度的基礎上增加了非隸屬度，從而能在處理模糊性決策問題時更好地表達不確定性。然而直覺模糊集的域與模糊集相同，仍然是離散集。為了克服這種限制，相關文獻將離散直覺模糊集擴展到連續直覺模糊集。連續直覺模糊集可以處理不同維度的信息，主要包括三角形直覺模糊集和梯形直覺模糊集。三角形直覺模糊集和梯形直覺模糊集的隸屬度和非隸屬度是三角形模糊數和梯形模糊數。多邊形模糊數是一個分段線性隸屬函數的概念推廣以及線性插值模糊數參數表示模糊數的一個特殊情況，在模糊信息處理中具有明顯的優勢。文獻[3]研究了一種基于多邊形模糊數概念的新數學形式化方法，它可以自然擴展到更高維的多邊形模糊集，并將多邊形模糊數成功應用于模糊神經網絡的構建。作為模糊集的擴展形式，多邊形模糊集近似為一般有限的模糊集，并能克服基于Zadeh的擴展原理的模糊組算術運算的復雜性。文獻[4]基于直覺模糊集和多邊形模糊集提出了n-直覺多邊形模糊集（n-intuitionistic polygonal fuzzy sets），給出了n-IPFSs的算術運算和漢明距離，并將該方法應用于多屬性決策問題。n-直覺多邊形模糊集是三角形直覺模糊集或梯形直覺模糊集的泛化，借助于有序實數描述模糊信息，并且可以根據任意精度調節模糊集的復雜性和近似模糊集的效果，更生動地描述了客觀事物的模糊性，使模糊信息處理更準確。作為梯形直覺模糊集或三角形直覺模糊集的推廣，n-IPFSs可以克服決策信息的不完整或不準確描述的缺點，并使模糊信息處理更準確。

信息測量在決策理論的發展及應用中起著至關重要的作用。距離測度是衡量決策中不同參數偏差的常用工具，用于比較替代方案和理想方案的接近或遠離的程度，獲取最優選擇。目前n-IPFSs的研究尚處于初級階段，其距離算子的相關研究較少。常見的距離算子包括：算數平均算子、幾何平均算子、加權平均算子。文獻[5]基于有序加權平均算子的思路提出了有序加權距離（OWD）算子，其主要的優點是其能夠通過對極大或極小的偏差賦予較低或較高的權重，從而削減或加強這些偏差對集結結果的影響。文獻[6]開發了猶豫模糊有序加權距離算子（HFOWD）。文獻[7-8]將有序加權距離應用到畢達哥拉斯模糊情境中。文獻[9-12]將有序加權距離測度拓展到直覺模糊集中。文獻[13]提出了多人多準則誘導有序加權平均距離算子（MP-MC-IOWAD）。

本文從有序加權視角研究n-直覺多邊形模糊有序加權距離測度并將其運用到多屬性決策中。首先，提出n-直覺多邊形模糊距離算子（n-IPFOWD），并給出其權重計算方法；其次，提出了一種基于n-IPFOWD的n-直覺多邊形模糊多屬性決策方法；最后，通過案例應用說明其可行性和有效性。

1 基本概念

1.1 n-直覺多邊形模糊集

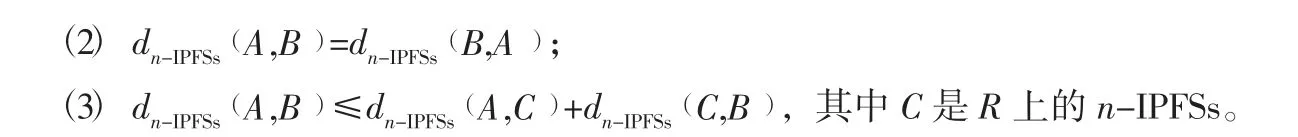
定義4：設是R上的一個n-直覺多邊形模糊集，n∈N，其得分函數為：

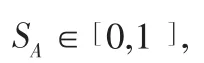
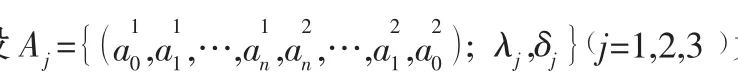
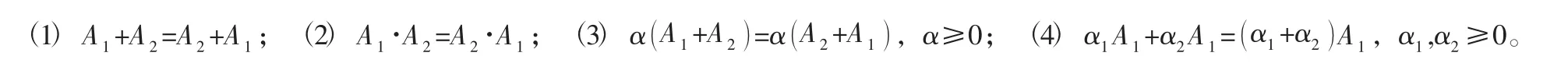
1.2 有序加權距離算子

基于OWA算子的思路，Xu和Chen提出有序加權距離（OWD）算子，定義如下：

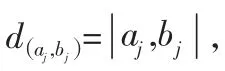
特別的，當λ=1，λ=2和λ→0時，OWD測度分別稱為有序加權平均距離算子（OWHD），有序加權Euclidean距離算子（OWED）和有序加權幾何距離算子（OWGD）。

2 n-直覺多邊形模糊有序加權距離算子

在n-直覺多邊形模糊集距離測度和有序加權距離算子的基礎上，定義n-直覺多邊形模糊有序加權距離算子。

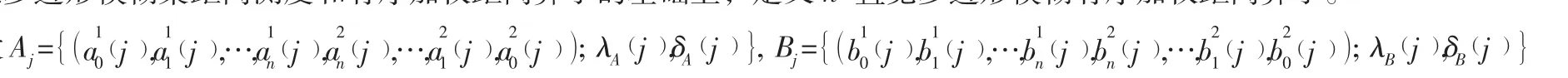
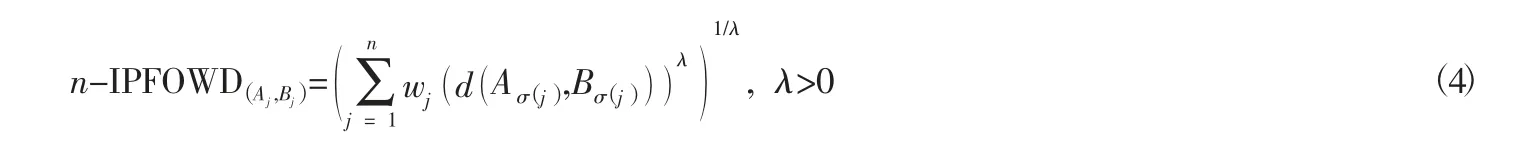
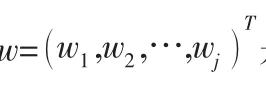
當λ=1，λ=2和λ→0時，可將n-IPFOWD算子分別稱為n-直覺多邊形模糊有序加權平均距離算子（n-IPFOWHD），n-直覺多邊形模糊有序加權Euclidean距離算子（n-IPFOWED）和n-直覺多邊形模糊有序加權幾何距離算子（n-IPFOWGD）。

從式（4）中發現，n-IPFOWD相關聯的權重向量如何確定是關鍵，下面基于A和B之間的漢明距離給出一種與n-IPFOWD相關聯的權重計算方法。

3 基于n-IPFOWD的n-直覺多邊形模糊多屬性決策方法

假設一個n-直覺多邊形模糊多屬性決策問題包括m個備選方案和n個評價指標，令G={g,g,…,g}表示方案集，C息，得到一列決策矩陣Y。根據n-IPFOWD算子，給出解決n-直覺多邊形模糊多屬性決策問題的方法。具體步驟如下：

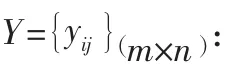
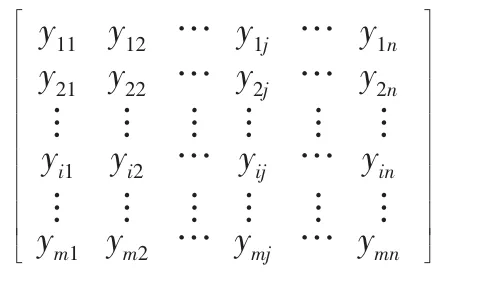
步驟二：建立標準化的n-IPFSs的評估矩陣H=h{}：

步驟三：用熵權法確定屬性權重：

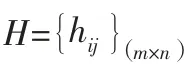
（2）根據得分值的歸一化結果，得到信息熵e，其中如果l=0，則lln=0：

（3）利用信息熵方法計算第j個屬性的權值q：

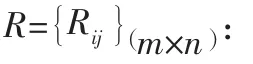
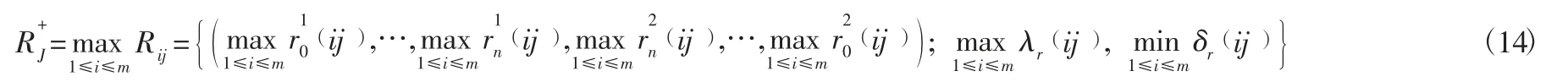
成本型指標的理想解如下：

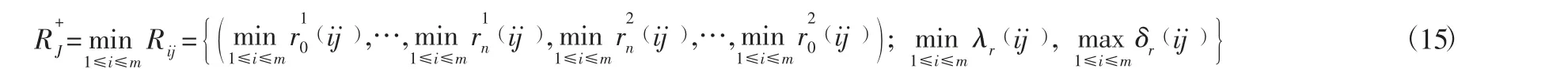
步驟六：應用n-IPFOWD算子，計算備選方案與理想方案之間的距離d（i=1,2,…,n）：

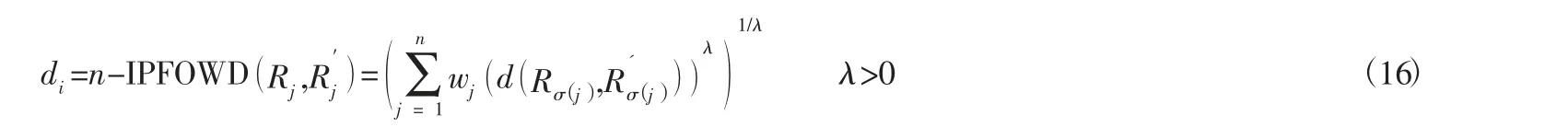
當λ=1，λ=2和λ→0時，d可分別表示在n-IPFOWHD算子、n-IPFOWED算子以及n-IPFOWGD算子下備選方案與理想方案之間的距離。

步驟七：將d,d,…,d按從小到大排序，則距離最小所對應的方案為最優方案。

4 實例應用

建筑行業是我國的重要產業，據統計，中國建筑材料工業2020年二氧化碳排放14.8億噸，比上年上升2.7%。此外，建筑材料工業的電力消耗可間接折算約合1.7億噸二氧化碳排放量。其中墻體材料工業二氧化碳排放1322萬噸，墻體材料工業的電力消耗可間接折算約合612萬噸二氧化碳排放量。隨著國家生態文明發展觀的提出和科學技術的進步，以及碳達峰的戰略目標下，越來越多的企業也開始將綠色環保環境因素納入其合作企業考核評價體系中。W企業多年來始終服務于國家戰略，投身綠色發展理念的實踐當中，經過50多年來的不斷努力，W企業已經確保了綠色施工領域的行業領先地位。W企業現準備為在建設的綠色科技示范樓采購一批墻面裝修涂料，經過初選有g,g,g,g和g五家實力較強的企業進入最終的評選階段。假設根據以下五個指標選擇綠色環保能力強的合作企業：產品對環境的無害性（c）、能源低碳化（c）、企業生產潔凈化（c）、廢物資源化（c）和企業發展可持續化（c）。邀請相關專家組建決策團對合作企業進行評價，語言術語為S＝{S＝很差，S＝差，S＝較差，S＝中等，S＝較好，S＝好，S＝很好}。在n-IPFSs中，n作為一個變量保持了線性運算的緊密性。假設n=3，采用3-直覺多邊形模糊集表達專家評估語言信息，評估語言信息與3-直覺多邊形模糊集之間的轉換標準如表1所示。

(2)一定要對所設計的系統有一個清晰的思路，例如哪些設備的管路需要開啟/關閉，哪些管路的流量需要調節，哪些運行參數需要監測，哪些設備或者管路工作時需要安全保護等。這一方面需要專業理論知識的支持，更重要的是要經常去已建成并投入使用的冷、熱源系統機房參觀、調研，掌握系統的運行方式和特點，才能做到合理地配置配件。

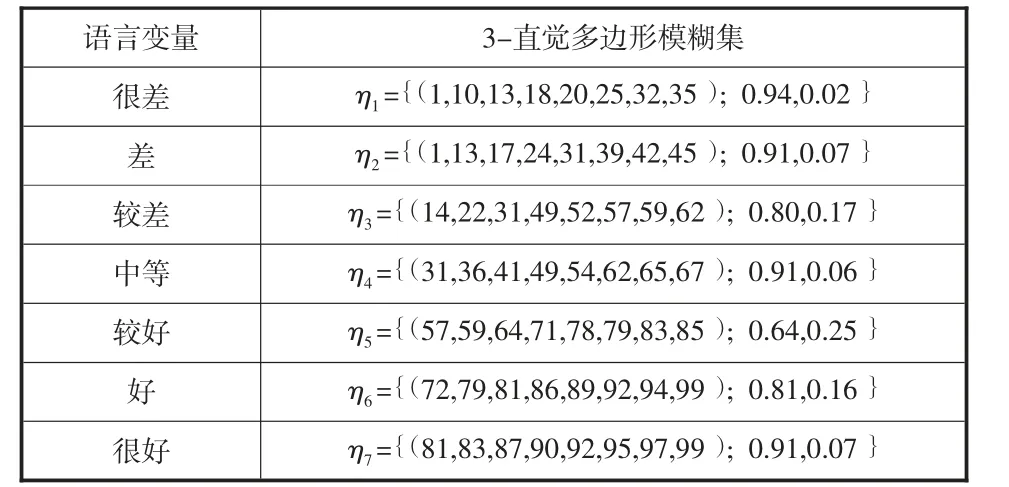
表1 評估語言信息與3-直覺多邊形模糊集之間的轉換標準

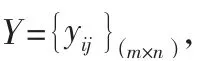
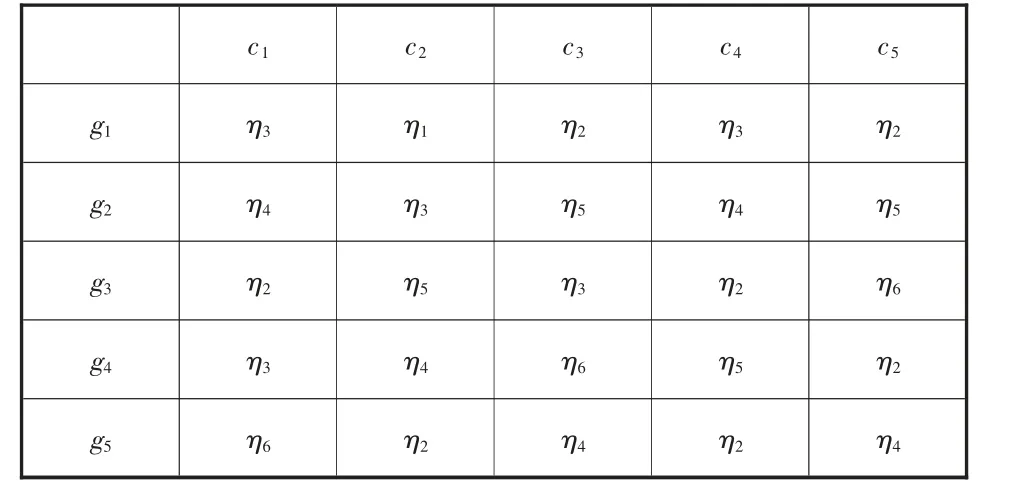
表2 專家評估矩陣Y

步驟二：構建標準化評估矩陣；使用公式（6）和公式（7）獲取θ，θ=99,θ=85,θ=99,θ=85,θ=99，得到專家評估信息的標準化結果。企業g的標準化評估信息如下所示：

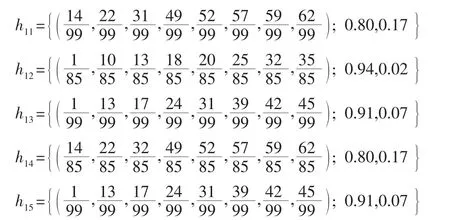
步驟三：用熵權法確定屬性權重。

首先采用公式（10）得到各企業的歸一化得分值為l=0.1548，l=0.1280，l=0.1259，l=0.1907，l=0.1295，l=0.2445，l=0.1970，l=0.1588，l=0.3012，l=0.1634，l=0.1265，l=0.2030，l=0.1541，l=0.1558，l=0.3272，l=0.1548，l=0.3111，l=0.3179，l=0.1965，l=0.1295，l=0.3194，l=0.1609,l=0.2433，l=0.1558，l=0.2504。再采用公式（11）和公式（12）得到各指標信息熵（e）以及熵權（q），計算結果如表3所所示。

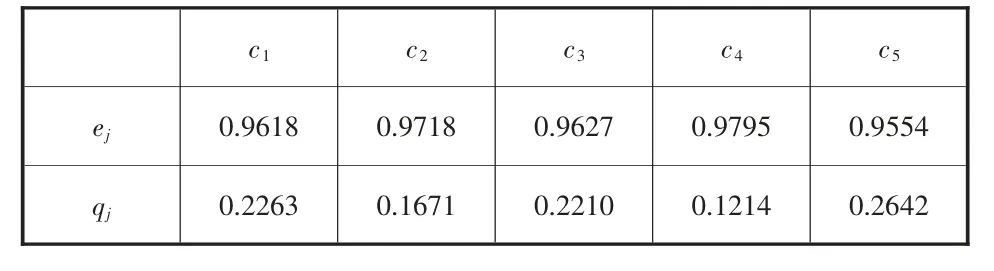
表3 信息熵和熵權值計算結果

步驟四：運用公式（13）建立加權標準化評估矩陣R={R}），部分加權標準化評估信息結果如下：

步驟六：運用n-IPFOWD算子，采用公式（16）并令λ=1，λ=2和λ→0，分別計算各備選方案g（i=1,2,…,n）與理想方案在n-IPFOWHD算子、n-IPFOWED算子以及n-IPFOWGD算子下的距離d（i=1,2,…,n）；計算結果如表4所示。

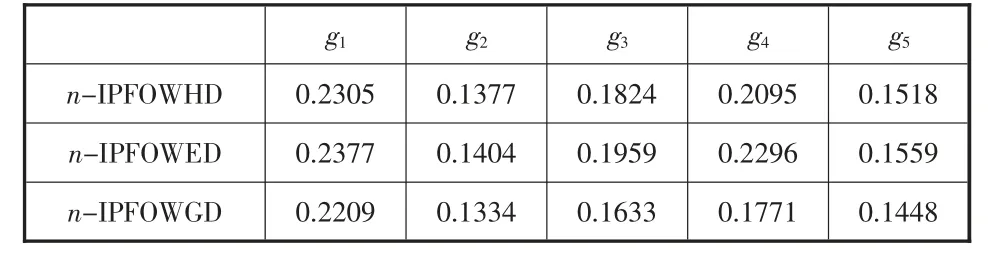
表4 備選方案與理想方案在各種有序加權距離算子下距離

步驟七：將d,d,…,d按從小到大排序，則距離最小所對應的方案為最優方案。

依據距離大小對企業進行排序，距離越小對應的企業綠色環保能力最強。不同有序加權距離算子下的排名結果是相同的，g始終是最佳方案，即企業g是綠色環保能力最強的企業。圖1表示出在不同有序加權距離算子下的各企業與理想方案的接近度比較。

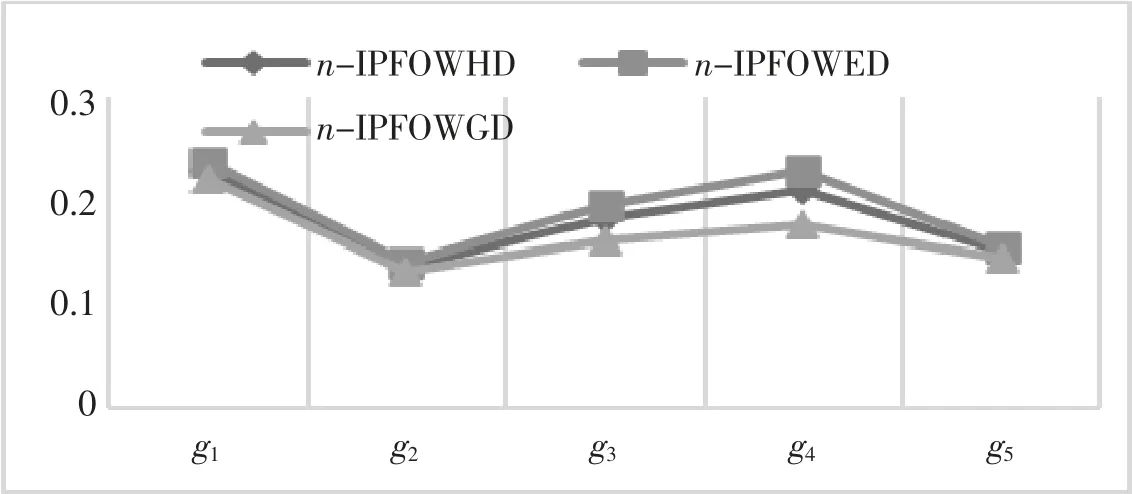
圖1 不同有序加權距離算子下各企業的排名結果

由以上分析可知，本文提出的n-IPFOWD算子可以對n-直覺多邊形模糊集的語義信息進行有效處理。n-直覺多邊形模糊集借助于有序實數描述模糊信息，可以根據任意精度調節模糊集的復雜性和近似模糊集的效果，生動地描述了客觀事物的模糊性，使模糊信息處理更準確。n-IPFOWD算子不僅強調集成數據的重要性，而且體現數據所在位置的重要性，可以通過對較大的偏差賦予較高的權重，從而削減這些偏差對集結結果的影響。專家可以根據風險偏好和實際問題選擇合適的參數λ，從而為決策者提供更多的選擇。

5 結束語

作為三角形直覺模糊集和梯形直覺模糊集的拓展形式。n-直覺多邊形模糊集可以根據任意精度調節模糊集的復雜性和近似模糊集的效果，使模糊信息處理更準確。目前n-IPFSs的研究尚處于初級階段，其距離算子的相關研究較少。本文從有序加權視角研究了n-直覺多邊形模糊距離算子（n-IPFOWD）及其在多屬性決策中的應用。首先，定義了n-直覺多邊形模糊距離算子n-IPFOWD，該距離算子能夠有效削減信息偏差，提高決策的科學性和合理性。其次提出了一種基于n-IPFOWD的n-直覺多邊形模糊多屬性決策方法。通過利用n-IPFOWD計算備選方案與理想解的距離，根據大小選擇最優方案，該方法拓展了n-IPFOWD的應用，豐富了n-直覺多邊形模糊集的研究成果。最后通過綠色供應商評價案例結果說明了本文所研究方法的有效性和靈活性。