一種優化的灰狼算法
楊寒石, 吳皓月, 孔德貴
(1.黑龍江大學 電子工程學院, 哈爾濱 150080; 2.黑龍江大學 計算機科學技術學院, 哈爾濱 150080)
0 引 言
傳統灰狼算法(Grey wolf algorithm,GWA)是一種模擬狼群狩獵行為的智能算法,已經廣泛應用于無人機航路規劃和電機控制等研究領域[1-4]。然而,GWA算法存在局部開發能力較弱、早熟收斂和初始種群分布不均勻等問題。針對這些問題,學者們主要從種群初始化、控制參數、狼群搜索機制以及灰狼位置更新策略等方面對GWA算法進行了優化[5-7]。2015年,Saremi等將進化種群動態算子(Evolutionary population dynamic, EPD)引入到GWA算法中,顯著提高了算法的局部搜索能力和收斂速度[8]。2017年,龍文等采用佳點集法替代GWA算法中利用隨機數初始化種群的方法,增加了初始種群的多樣性[9]。2020年,甄永琦等將差分進化算法(Differential evolution algorithm,DEA)與GWA算法相結合,利用DE算法的交叉算子和變異算子改進灰狼位置更新公式,提高了GWA算法的局部開發能力[10]。2020年,劉彬等利用競爭策略動態更新α狼、β狼和δ狼的位置,提高了GWA算法的全局搜索能力[11]。2021年,王穎等結合云模型理論,通過動態權重法調整收斂因子,平衡GWA算法的全局搜索和局部開發能力[12]。2021年,Mohammad等將維度學習搜索策略(Dimensional learning high,DLH)引入傳統灰狼算法,提高了算法的全局搜索能力和標準測試函數的尋優精度[13]。這些對GWO算法的優化均未考慮灰狼個體經驗對灰狼位置更新的影響以及算法后期種群多樣性喪失的問題,會導致GWO算法局部開發能力差、過早收斂和收斂精度低等問題。針對這些問題,本文從四個方面優化了傳統的GWO算法,這里稱之為優化的灰狼算法(Optimized grey wolf agorithm, OGWA)。第一,利用Cat映射和反向學習初始化種群,增加初始種群的多樣性;第二,在灰狼位置更新公式中引入粒子群算法(Particle swarm optimization,PSO)的個體經驗公式,避免算法提前收斂停滯;第三,用非線性控制參數替換傳統灰狼算法的線性控制參數,使收斂因子在算法前期緩慢遞減,在后期迅速遞減,改善了算法的搜索能力和開發能力;第四,利用Levy飛行理論對α狼進行全局搜索,維持算法后期種群的多樣性,降低算法后期陷入局部最優的風險。通過與GWA算法、PSO算法和蟻群算法(Ant colony optimization,ACO)的仿真比較發現,LIGWA算法具有較高的求解精度和良好的穩定性。
1 傳統灰狼算法
GWA算法是一種通過模擬灰狼群體等級制度和狩獵行為來實現參數尋優的算法。GWA算法中將灰狼群體分為四個社會等級:第一等級是灰狼群體的領導者,稱為α狼,負責對狼群的狩獵對象、棲息地選擇等決策;第二等級稱為β狼,負責協助α狼管理群體;第三等級稱為δ狼,主要負責偵察和狩獵等工作;第四等級稱為ω狼,社會地位最低,需要服從前三個等級狼的領導。
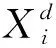
(1)
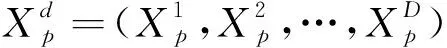
(2)
(3)
式中:Rand1和Rand2表示[0,1]間的隨機數;a為線性控制參數,其值隨著迭代次數的增大線性遞減,計算如式(4)所示:
(4)
式中tmax為最大迭代次數。
在灰狼狩獵過程中,當種群搜索到獵物位置時,α狼、β狼和δ狼距離獵物位置最近,因此,可以依據α狼、β狼和δ狼的位置Xα、Xβ和Xδ計算灰狼向獵物移動的位置,具體如式(5)~式(8)所示。
首先由式(5)~式(7)計算出其余灰狼的移動方向。
(5)
(6)
(7)
然后由式(8)更新灰狼的位置:
(8)
2 優化的灰狼算法
2.1 Cat混沌映射和反向學習相結合的種群初始化策略
2015年,劉建軍等采用混沌映射初始化種群,可以增加初始種群的均勻性;2019年,張新明等在種群初始化的過程中引入反向學習理論可以增加初始種群的多樣性[14-15]。本文將Cat混沌映射和反向學習兩種方法相結合對種群進行初始化,提高初始種群的多樣性和均勻性。Cat混沌映射具有較好的遍歷均勻性,可以使初始種群均勻分布,Cat映射的數學描述如式(9)所示[16]:
(9)
利用Cat混沌映射和反向學習初始化種群,首先,要利用Cat混沌映射產生N×D維初始解矩陣C,這里N代表種群規模,D代表維度。然后,利用反向學習理論為C中的每個初始解產生與之對應的反向解,得到反向解矩陣O,計算公式為:
(10)
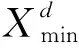
最后對初始解矩陣C和反向解矩陣O合并,得到2N×D維解矩陣J,對J中D個列向量的元素從小到大進行排序,選取每一個列向量中較小的前N個元素作為初始解,組成N×D維的優良種群矩陣。
2.2 引入粒子群個體位置更新策略
在灰狼狩獵的過程中,從式(5)~式(8)可以看出,灰狼的位置主要是根據α狼、β狼和δ狼的位置Xα、Xβ和Xδ進行更新的,在位置更新中忽略了灰狼個體經驗,容易導致算法過早收斂[17-18]。相比較而言,PSO算法在位置更新方面有不容易過早收斂的優勢。在優化的灰狼算法中,利用PSO算法中更新粒子個體位置信息的方法更新灰狼個體的位置信息,灰狼位置更新式(8)可以寫成式(11):
(11)
式中,灰狼個體位置更新公式:
vdi(+1)=w·(vdi(t)+G1·Rand3·(Xdi,α-Xdi(t))+G2·Rand4·(Xdi,β-Xdi(t))+G3·Rand5·(Xdi,δ-Xdi(t)))
(12)
G=2×Rand
(13)

2.3 非線性控制參數策略
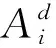
(14)
式中:t為當前的迭代次數;tmax為最大迭代次數。
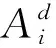
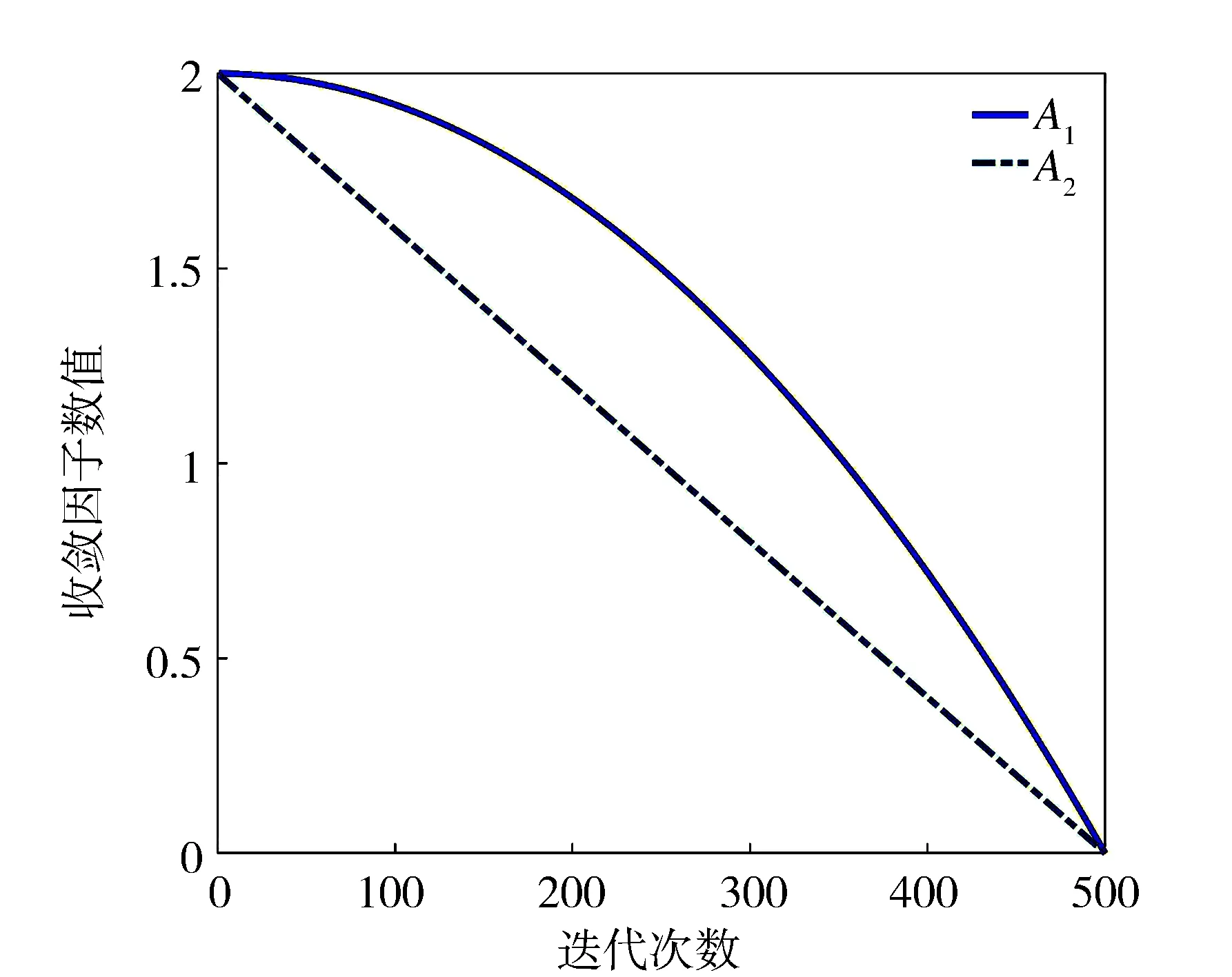
圖1 收斂因子的變化曲線
2.4 引入Levy飛行更新α狼位置
在GWA算法中,α狼的位置代表最優解。在搜尋獵物的過程中,所有的灰狼均向α狼靠近,這會導致種群在迭代過程中逐漸失去多樣性,使算法過早收斂[22]。針對這一不足,利用Levy飛行對α狼進行位置更新,α狼位置更新公式為:
(15)
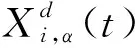
b=Random(size(αposion))
(16)
(17)
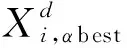
(18)
(19)
式中σu和σv分別由式(20)和式(21)計算:
(20)
σv=1
(21)
2.5 LIGWA算法步驟
綜上所述,優化灰狼算法(LIGWA)的實現步驟如下:
Step1: 設置種群規模N、個體學習參數G1、G2、G3、δ和tmax。
Step2: 利用上面所述Cat映射和反向學習產生初始種群Xi,i=1,2,…,N。
Step3: 計算種群中灰狼個體的適應度值并從小到大排序,將適應度值最小的灰狼位置作為歷史最優解Xα,適應度值第二小的灰狼位置作為第二最優解Xβ,適應度值第三小的灰狼位置作為第三最優解Xδ。
Step4: 利用式(15)~式(21)對α狼進行全局搜索,更新α狼的位置。
Step5: 利用式(14)計算非線性控制參數a*,按照式(2)更新收斂因子。
Step6: 對除Step 3中確定的α狼、β狼和δ狼之外的灰狼個體按式(5)~式(7)計算灰狼移動方向。
Step7: 利用式(11)更新灰狼位置。
Step8: 判斷算法當前的迭代次數是否達到最大迭代次數tmax,若滿足,則輸出α狼的適應度值,否則返回執行Step 3重新計算適應度值,更新Xα、Xβ和Xδ。
3 仿真實驗與分析
3.1 標準測試函數
為了測試LIGWA算法的性能,選取6個標準測試函數進行仿真實驗,函數的表達式如表1所示。其中f1~f3為單峰函數,用來檢驗算法的尋優精度;f4~f6為連續多峰函數,用來檢驗算法后期的局部開發能力。

表1 標準測試函數
3.2 與GWA算法的比較分析
利用LIGWA算法和GWA算法分別對表1的函數進行求解。仿真實驗中兩種算法的狼群規模均為N=30,tmax=1 000。兩種算法分別獨立運行30次,求解函數的最優值、最差值、平均值和標準差。最優值代表算法求解函數得到的最小值,最差值代表算法求解函數得到的最大值,平均值代表算法的求解精度,標準差代表算法的穩定性。仿真實驗結果如表2所示,函數收斂曲線如圖2~圖7所示。
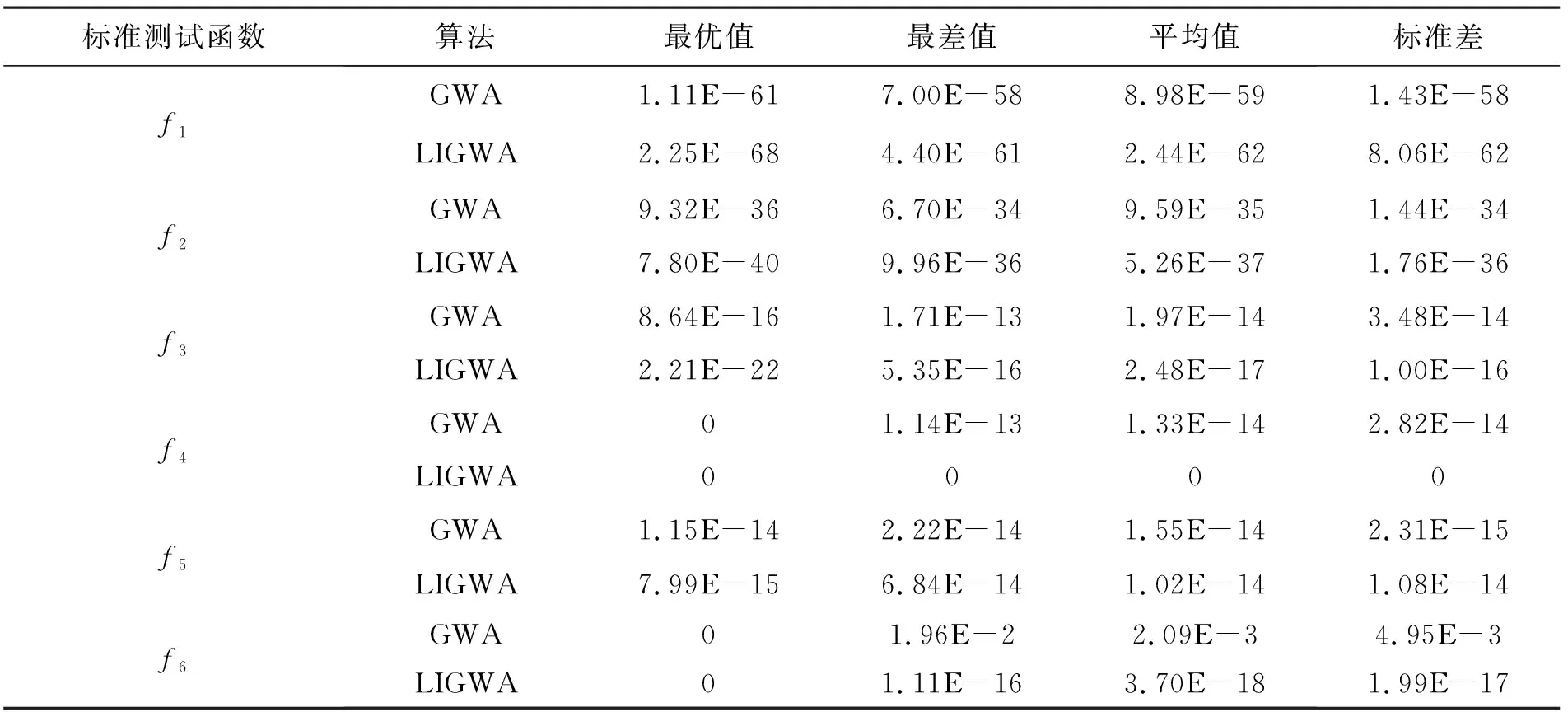
表2 LIGWA算法和GWA算法的仿真實驗結果對比
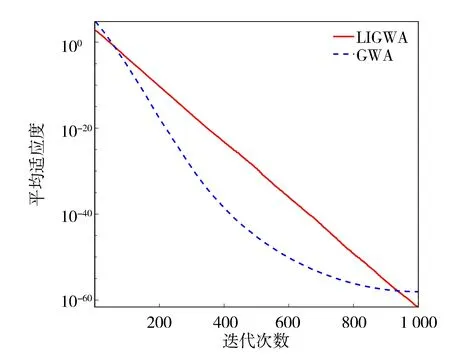
圖2 函數f1的收斂曲線
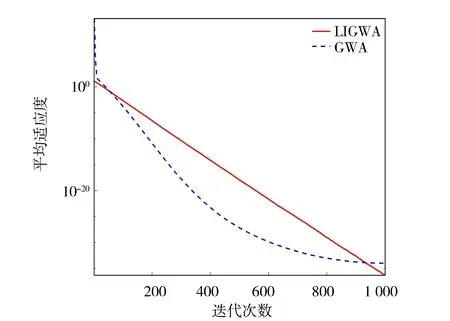
圖3 函數f2的收斂曲線
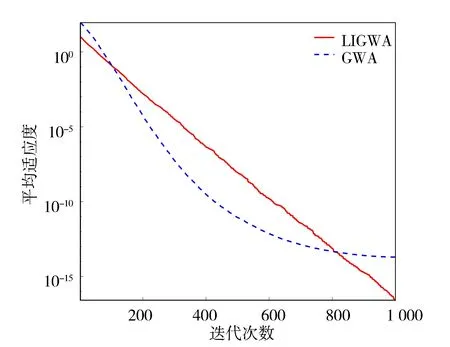
圖4 函數f3的收斂曲線
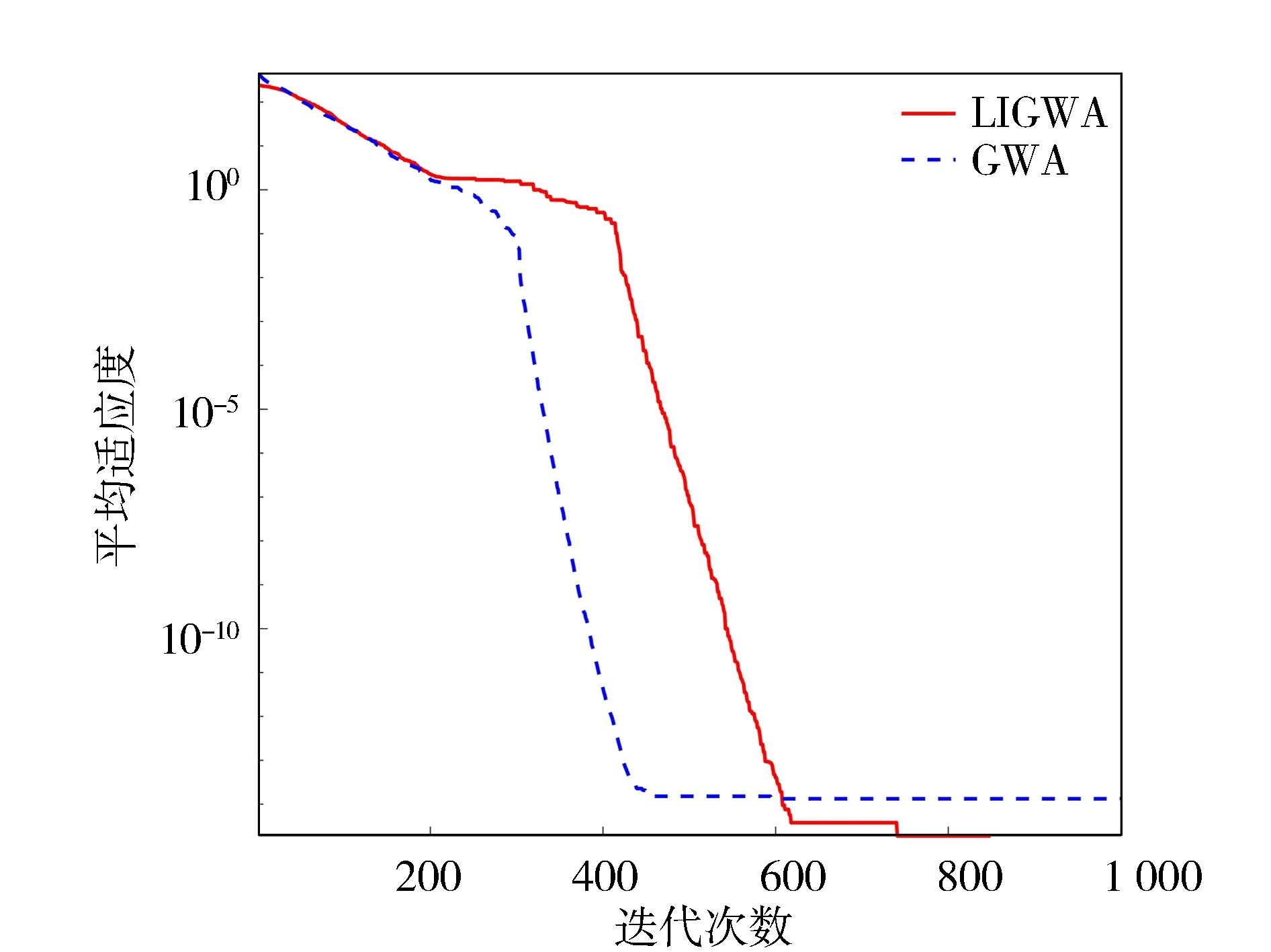
圖5 函數f4的收斂曲線
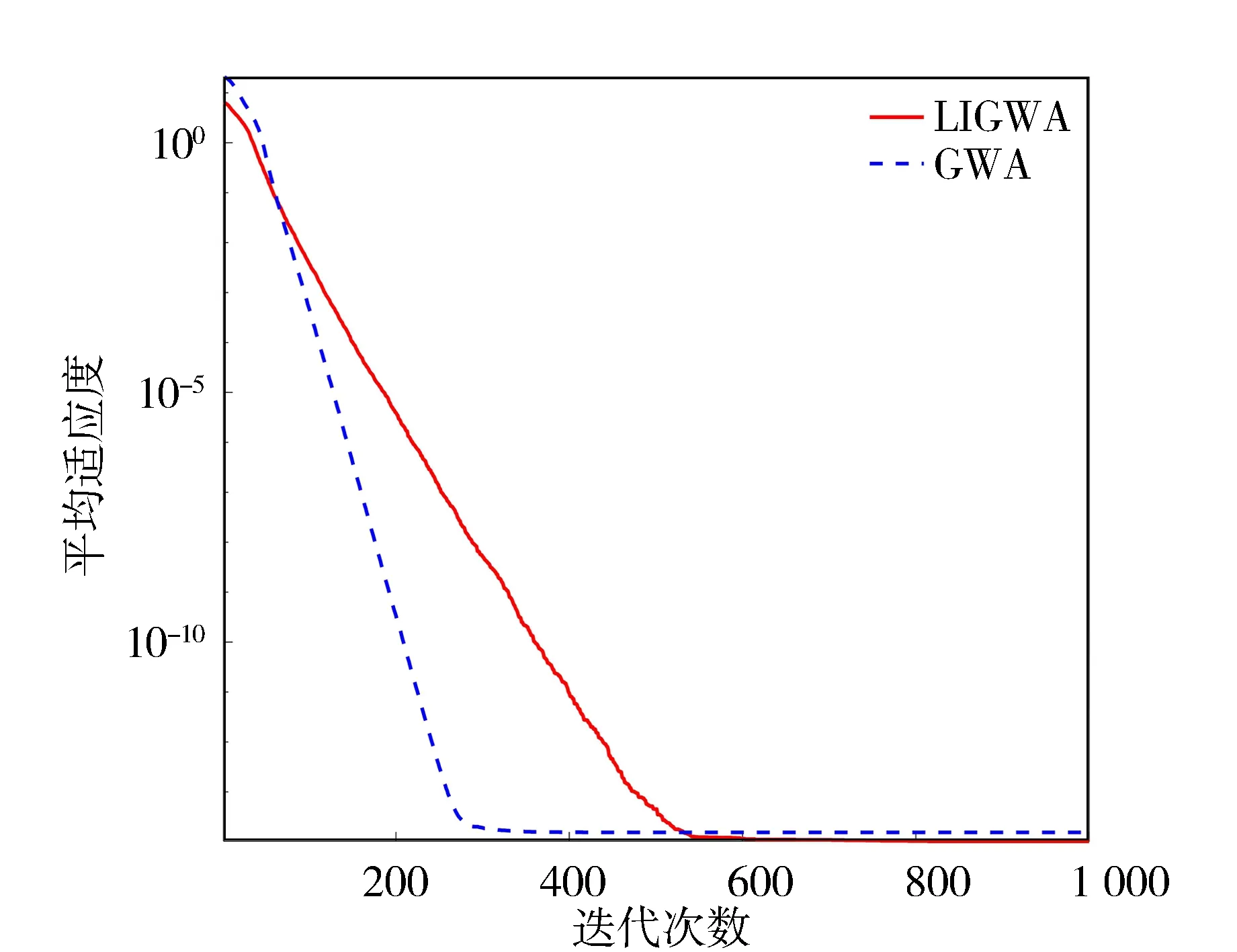
圖6 函數f5的收斂曲線
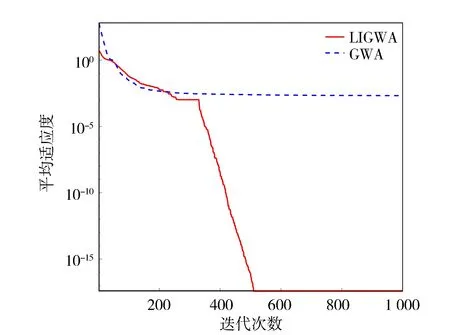
圖7 函數f6的收斂曲線
從表2中的對比結果可知, LIGWA算法在6個標準測試函數上的求解精度均優于GWA算法,其中在函數f6的計算上,LIGWA算法的求解精度高出了GWA算法大約1 015個數量級,說明LIGWA算法能有效地提高全局搜索能力,降低算法后期陷入局部最優的風險。LIGWA算法在函數f1~f4、f6上的標準差小于GWA算法,而在函數f5上的標準差比GWA高出1個數量級,表明LIGWA算法在大部分測試函數上具有較好的穩定性。
由圖2~圖4可以看出,LIGWA算法的求解精度明顯高于GWA算法,說明LIGWA算法能有效地提高算法前期的全局搜索能力和函數求解精度。由圖5~圖7中可以看出,GWA算法在種群迭代到500代之前就已經收斂,而LIGWA算法在迭代到500代之后才開始收斂,說明LIGWA算法能夠提高局部開發能力,改善了GWA算法后期容易陷入局部最優和GWA算法收斂早熟的缺陷。由圖2~圖7也可以看出,相比于GWA算法,LIGWA算法的收斂速度較慢,這是由于LIGWA算法在灰狼位置更新過程中考慮了灰狼個體經驗對位置更新的影響,灰狼位置更新公式變得復雜,增加了計算時長。所以,LIGWA算法是以犧牲收斂速度來提高函數求解精度以及平衡全局搜索和局部開發能力的。
3.3 與其他算法的比較分析
為進一步測試LIGWA算法的性能,將其與PSA算法和ACA算法進行對比分析,實驗結果如表3所示,其中PSO算法和ACO算法的仿真實驗結果來源于徐辰華等數據[23]。
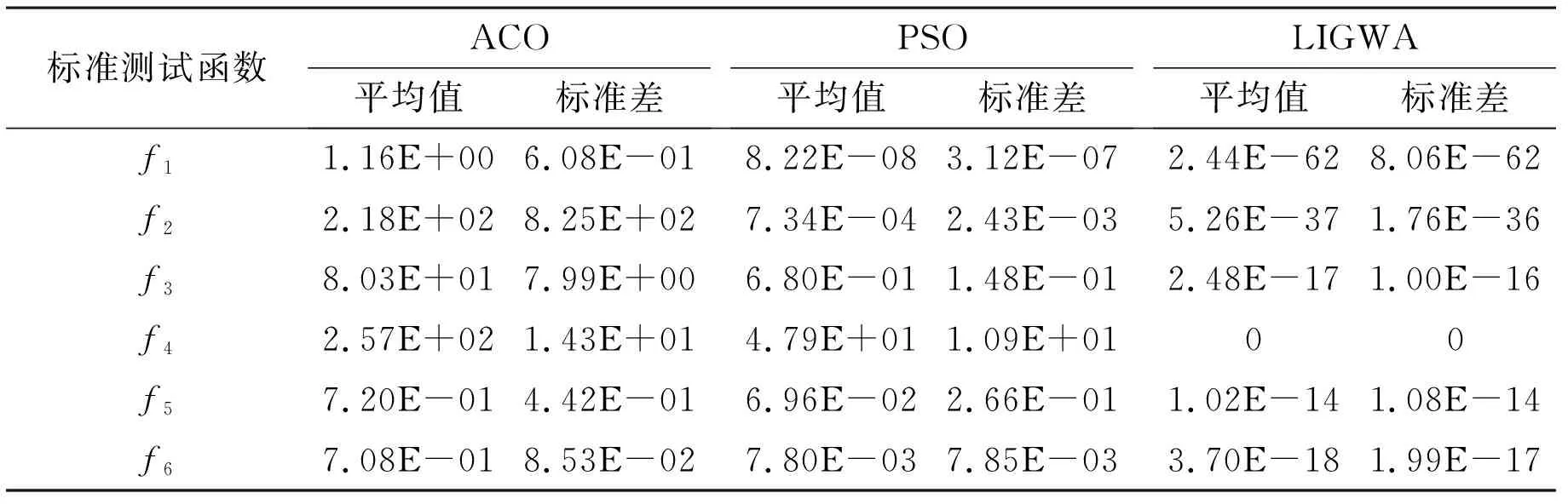
表3 不同算法的仿真實驗結果對比
從表3可以看出,在單峰函數和多峰函數的求解精度上,LIGWA算法的求解精度明顯優于PSO算法和ACO算法,其中在函數f4的求解上,LIGWA算法的求解精度達到了函數最小值0;在算法穩定性上,LIGWA算法在函數f1~f6的標準差均小于PSO算法和ACA算法,其中LIGWA算法在函數f4上的標準差達到了0,證明本文提出的LIGWA算法是可行的。
4 結 論
為了解決傳統灰狼算法存在局部開發能力弱、早熟收斂和初始種群分布不均勻等問題,提出了一種優化的灰狼算法。通過求解6個標準測試函數并與GWA算法、PSO算法和ACO算法進行對比,證明了優化灰狼算法具有較高的求解精度,改善了GWA算法早熟收斂的缺點,提高了GWA算法后期的局部開發能力,能夠有效地處理單峰和連續多峰函數的尋優問題,解決神經網絡、支持向量機和極限學習機等機器學習算法中目標函數的優化問題。

