基于EEG 信號特征提取與SVM 算法的睡眠自動分期*

張 章 周新淳 趙鴻浩 張雪華

（1.寶雞職業技術學院機電信息學院 寶雞 721000）（2.寶雞文理學院物理與光電技術學院 寶雞 721016）（3.陜西烽火通信集團有限公司寶雞研發中心 寶雞 721006）

1 引言

睡眠是人類生命活動的基礎需求之一，從日常的生活經驗中可以發現，提高學習效率和記憶力的一個前提條件就是保證充足的睡眠［1］。睡眠性疾病與個人精神狀態有關，往往難以發現和確診，因此對睡眠數據進行分析是發現和診斷與睡眠有關的疾病和加速睡眠相關的研究是十分重要的，而睡眠分期任務就是睡眠數據分析中必不可少的一個工作［2］。腦電信號（Electroencephalogram，EEG）是睡眠數據中的一個重要采集內容，它含有豐富的與大腦生理活動相關的信息，作為生物電信號，它的變化特性極其復雜，是神經醫學類學科分析病理和判斷病情著重參考的一個信息，它還能準確反映大腦的活動狀況，在睡眠研究中應用逐漸普遍［3］。通過檢測平臺所記錄下的EEG 信號數據量大，希望人工判斷會大大增加醫生或相關人員的工作量，會花費大量時間，降低工作效率增加治療周期，并且因為主觀性高也會容易引起較大爭議。尋找一種可以根據EEG 信號特點來完成睡眠數據快速準確的自動分期方法成為了解決睡眠分期問題的重要途徑。

近年來許多學者通過引入模式識別的方法來完成EEG 信號的自動分期任務，其中被使用較多的方法有支持向量機（Support Vector Machine，SVM）和神經網絡等算法［4］。Anderer 等將決策樹的方法應用于睡眠分期取得了80%的準確率［5］。Zhang Junming 與Wu Yan 提出了基于復值卷積神經網絡（Complex-valued Convolutional Neural Network，CCNN）的新的睡眠階段分類系統，該方法通過對EEG 信號所提取的特征進行訓練學習，然后根據所學特征對睡眠階段進行分類，結果表明此方法的分類性能與收斂速度優于卷積神經網絡（Convolutional Neural Network，CNN）［6］。北京理工大學的由育陽等提出了一種基于正態逆高斯和特征貢獻度的睡眠分期實驗框架，并設計了多分類器組合自動睡眠分期算法，獲得了較高的準確率［7］。

本文提取了EEG 節律信號的能量特征，通過小波包分解可以提取EEG 信號節律波的能量特征［8］，除此之外還提取了其非線性特征計算每幀數據的排列熵和樣本熵，使用SVM 方法對劃分的測試集進行分類完成睡眠自動分期任務。

2 睡眠分期

2.1 EEG節律信號

EEG 里的信號有著一定的特征頻率范圍和空間分布特征，依據信號的頻率特性可以劃分出四種節律波。EEG 帶寬范圍為0～100Hz，但是節律波的有效信號在0～30Hz的范圍之內。

1）δ波（Delta）：頻率在0.5Hz～4Hz 之間，振幅在20μV～200μV 之間。δ波作為大腦中自發產生的頻率最低的信號波，會在人深度睡眠、深度麻醉缺氧或者大腦有器質性病變時被檢測到［9］。

2）θ波（Theta）：頻率范圍為4Hz～8Hz，振幅大概為10μV～50μV。θ波有著較低的頻率，正常情況下，人處于清醒狀態時大腦不會自發產生θ波，只有在困倦疲乏時，人的中樞神經系統受到抑制，此時會有θ節律波出現。

3）α波（Alpha）：頻率范圍為8Hz～13Hz，信號幅度在20μV～100μV 之間，檢測位置在頭枕部位。α波頻率較快，是EEG 中節律性最明顯的信號波。只有人在放松或者閉眼的狀態下，α波才能被穩定檢測到，一旦受檢者運動、睜眼或者想象運動時就會減少甚至消失。

4）β波（Beta）：頻率范圍在13Hz～30Hz之間，信號幅度為5μV～20μV。按照頻率不同，β波又可分為β1波和β2波兩種，是EEG 節律波中的一種快波。當這一頻段波被檢測到時，說明大腦皮層處在比較興奮的狀態，此時人思維比較活躍，可能正在進行邏輯思考或者情緒起伏較大［10～11］。因此β波可以認為是大腦清醒的標識。

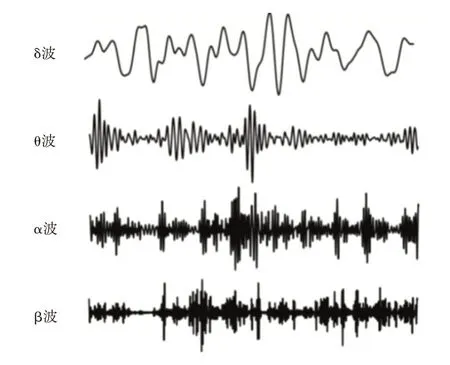
圖1 EEG信號4種節律波

2.2 睡眠時期劃分與各時期特點

1）睡眠時期劃分

在不同睡眠過程中，人的眼部電信號、腦部電信號等不同的生理電信號的變化特點有所區別，Anthony Kates 和Allan Rechtschaffen 以此為 依據提出了R&K 睡眠分期標準，在該標準中，睡眠一共被分為6 個時期即：W 期、R 期、睡眠I 期（S1）、睡眠II期（S2）、睡眠III 期（S3）、睡眠IV 期（S4）［12］，其中S1、S2、S3和S4同屬于NR期，按照這一標準來劃分的睡眠階段判斷此標準比較標準，因此R&K 睡眠分期標準的提出對睡眠分期的發展有巨大貢獻。

2）各睡眠時期特點

在不同的睡眠階段，每種基本特征波占比不同。在W 期α波和β波為主要部分，以α波的占比在50%以上。S1期α波的占比降到50%以下，以低幅θ波為主。S1 時期只是睡眠時期的一個過度階段，在總睡眠長度中占比較短，只占有總睡眠時間的5%左右。S2 期階段腦電信號的幅值增大，δ波占20%以下。此時雖然大腦為無意識狀態，但仍屬于淺睡眠時期還是容易受外界環境影響的，此睡眠時期的總長度應占睡眠的時期的45%左右。S3 和S4期的信號中以低頻δ波為主，占20%以上，現多被統一劃分為深度睡眠時期，由于在此期間腦電信號以δ波為主，所以也被稱為δ睡眠。深度睡眠時期受不易受外界影響，是人身體機能恢復的重要時期，時間長度占睡眠時間長度的20%左右。REM 期此階段伴隨眼球的快速自主轉動，除了尖峰波表現不明顯外，與S1期的波形相同。

3 算法步驟

3.1 EEG信號去噪處理

將特定的電極筆放置在受檢者頭皮表面，探測并記錄下各個點位的電勢差隨著時間的變化從而得到EEG 信號［13］。從頭皮處探測到的EEG 電信號通常十分微弱，容易受儀器本身所產生的噪聲影響，在對EEG 信號處理之前需要進行濾波平滑的預處理，這里選用小波域值去噪。

如前面所述，采集到的EEG 信號記錄的是各點位電勢差隨時間的變化，在時間域上有一定的連續性。在小波域上，有效連續性信號經分解計算得到的小波系數的模值通常數值較大，但是儀器本身所產生的噪聲一般為熱噪聲也就是高斯白噪聲，其在時間域上并不具備連續性，即使經過小波變換，高斯白噪聲在小波域上依然具有很強的隨機性［14］。因此在小波域上，有效連續性信號對應的系數遠大于噪聲所對應的系數，再利用閾值函數對小波系數進行處理，將處理過后的信號做小波重構，就可以得到EEG 去噪平滑之后的信號。在此過程中對于小波基函數的選擇、分解層數的不同和閾值規則的設計都會對EEG信號去噪平滑效果產生影響。

巴特沃斯濾波器可使通頻帶內的頻率響應曲線最大限度平坦，EEG 信號帶寬在0～100Hz，但是有效信號在0～30Hz 的范圍內所以，設定巴特沃斯帶通濾波器的采樣頻率為300（＞2*100），對小波濾波默認采用軟閾值濾波，選用Daubechies8 小波基，采用最大小波分解的層數，濾波后再進行小波重構。對一幀數據進行二階巴特沃斯帶通濾波和小波閾值濾波結果如圖2所示。

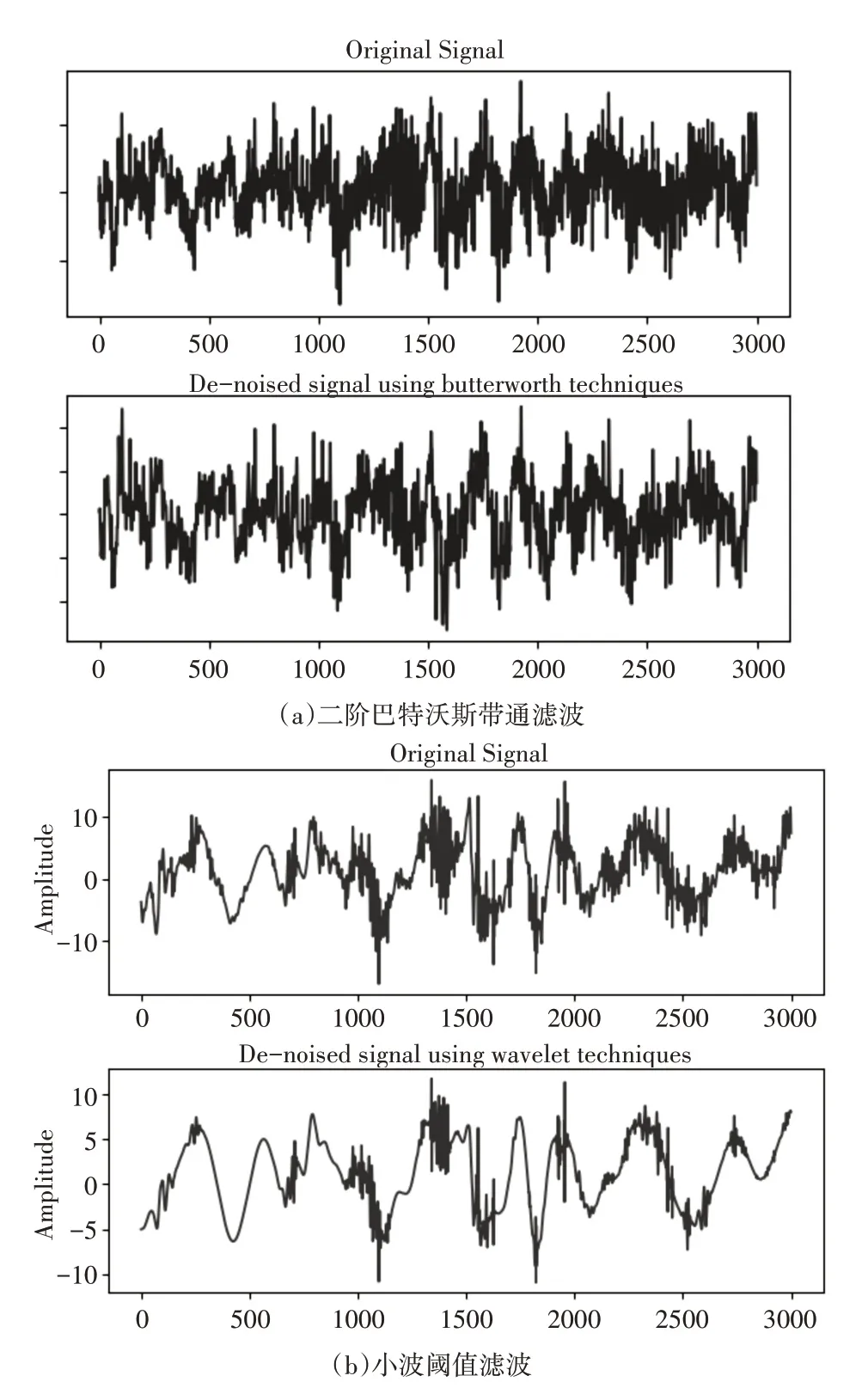
圖2 去噪濾波效果

對同一幀數據兩濾波器濾波情況對比，小波閾值方法對EEG 進行去噪處理后尖波噪聲信號和斷點有了明顯改善，同時EEG的峰值有較完整的保留。

3.2 節律波提取

對數據進行小波包分解（Wavelet Packet Decomposition，WPD）。小波分解（wavelet transform）無法對EEG 中的高頻部分繼續分解，與小波分解不同，小波包分解既可以對低頻部分進行分解重構，也可以對近似分量和細節分量再次分解從而分析信號的高頻部分［15～16］。針對不同頻率段的信號，小波包分解可以通過調整分解層數以調整頻率分辨率，選擇最優基函數，很大程度上提高了對信號局部分析的優勢。

對EEG 信號進行9層分解，按照采樣定律計算最小分辨率：

式中，fs為采樣頻率。

根據四個腦電節律的頻率范圍（0～30Hz），分別計算它們所包含的最少分解節點數，在計算時盡量選用低層節點，然后按照各節律波頻率設置相應的頻段濾波器。用［i，j］表示小波包分解的第i個節點到第j 個節點，同時考慮代小波包分解節點劃分存在頻帶交錯現象［17］。得到四個腦電節律所包含的分解節點及其對應的頻帶關系如表1所示。

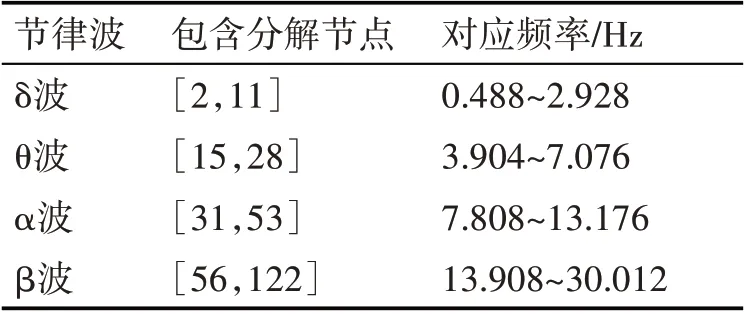
表1 節律波所包含分解節點與對應頻率

圖3 EEG節律波提取

3.3 能量特征提取

EEG 各節律波能量分別為：Eα、Eβ、Eδ、Eθ。不同睡眠時期能量也不相同，所以可以將能量作為睡眠分期的特征參數。信號g（t）的總能量表示為式（2）。

j 表示節律波；Ej表示對應節律波信號g（t）重構之后的能量值；i表示信號樣本的采樣點數量，i=0，1…m；xi表示重構信號的采樣點對應幅值。

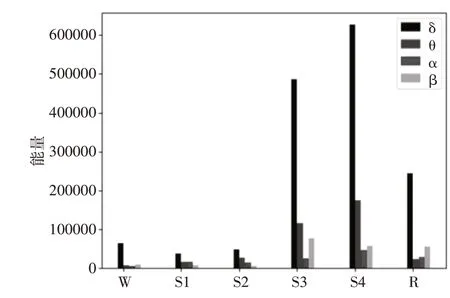
圖4 各時期節律波能量值

3.4 非線性特征提取

針對非線性數據，除提取能量特征外還需要提取非線性特征，計算每幀數據的排列熵和樣本熵。

3.4.1 排列熵計算

1）對時間序列X 進行相空間重構（相空間大小記為m），得到矩陣。矩陣的每一行都是一個相空間長度的序列［18］。

2）對矩陣的每一行按升序重新排列，排序后記錄該行排序前的下標順序得到一組符號序列。

3）統計每一行的下標順序出現的次數/m！，作為該行的概率，計算時間序列所有行的信息熵求和即為排列熵。

由以上計算步驟可知，當每一行的下標符號序列概率P=1/m！時，排列熵值，記為HPE，達到最大值。此時時間序列的復雜度越高（在符號序列中沒有重復的，或者重復的很少）。反過來，當HPE 值變小的時候，表示時間序列越規則。

3.4.2 樣本熵的計算

設原始數據時間序列長度為N 表示為{u(i)，1 ≤i≤N}，按如下步驟計算樣本熵：

1）構 造m 維 空 間 的 向 量X(1)，X(2)，…，X(N–m+1)，其X(i)={u(i)，u(i+1)，…，u(i+m-1)}。

2）將向量X(i) 和X(j) 之間的距離d[X(i)，X(j)]定義為X(i)和X(j)向量對應元素的最大差值，具體為d[X(i)，X(j)]=max|u(i+k)-u(j+k)|。

3）對于每一個{i，1 ≤i≤N-m+1}，在滿足容許偏差為r的條件下，統計d[X(i)，X(j)]＜r的個數，記為Nm(i)，計算Nm(i)的數目與向量間距離總數的比值計作Cmi(r)。

4）對于i求平均值計作φm(r)如式（3）。

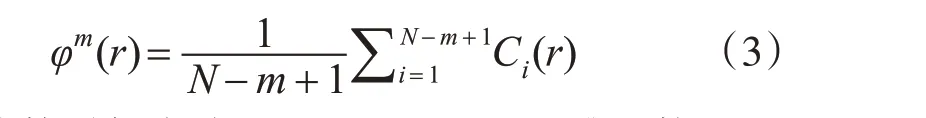
5）維數增加變成m+1后，對于m+1維重構后的序列向量重復上述步驟1）～4）得到Cm+1（r），φm+1(r)表示為式（4）和式（5）。

6）在N 取有限值的情況下此序列樣本熵為式（6）。

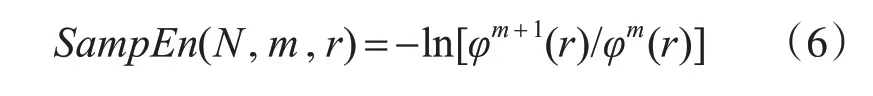
m=1或2時樣本熵值對信號序列的長度N依賴性最好［19］，此時計算得到的熵值較為合理。

3.5 支持向量機分類

支持向量機的基礎是Vapnik 所創建的統計學理論（Statistical Learning Theory，SLT），一種新的機器學習方法。統計學理論所采用的是結構風險最小化（Structural Risk Minimization，SRM）準則，這樣在得到最小化樣本點時，使得結構風險同樣取得最低，可以提高模型的適應性和泛化能力，并且不會受到數據維數的限制［20］。在進行線性分類時，將分類面取在離兩類樣本距離較大的地方；進行非線性分類時通過高維空間變換，將非線性分類變成高維空間的線性分類問題［20～22］。非線性映射是SVM 方法的理論基礎，SVM利用內積核函數代替向高維空間的非線性映射，對特征空間劃分的最優超平面是SVM 的目標，最大化分類邊際的思想是SVM 方法的核心。支持向量機有著以下優點：

1）支持向量是SVM 的訓練結果，在SVM 分類決策中起決定作用的是支持向量。因此，模型需要存儲空間小，算法魯棒性強；

2）無任何前提假設，不涉及概率測度。

4 實驗數據與結果

4.1 數據說明

此次數據為所采集EEG 信號中的一部分，共有8490000 個采樣點，采樣頻率100Hz，每幀數據3000 采樣點即30s 為一幀，共2830 幀，為不平衡數據。樣本標簽中，W，S1，S2，S3，S4，R，M 共有2830個。

睡眠階段為W，S1，S2，S3，S4，R，M（運動時間）和‘Unscored’（無法判斷）。

表2 數據說明

對無意義數據進行剔除，刪除標簽為9 和幀數只有1 的M 時期的數據，只針對有意義W，S1，S2，S3，S4，R進行分類。

4.2 實驗結果

本實驗軟件環境為Windows 10 操作系統，Pycharm Professional Edition，Python3.9，硬件環境為Intel（R）Core（TM）i5-10200H CPU，NVIDIA Ge-Force RTX 2060GPU。根據提取的特征表，使用SVM 分類模型進行分類，訓練集與測試集比例為7∶3；得到分類結果，其準確率為84.45%。

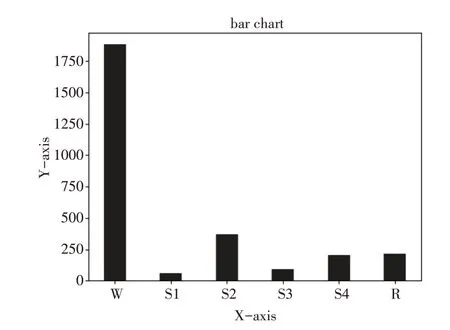
圖5 各睡眠時期在數據中占比

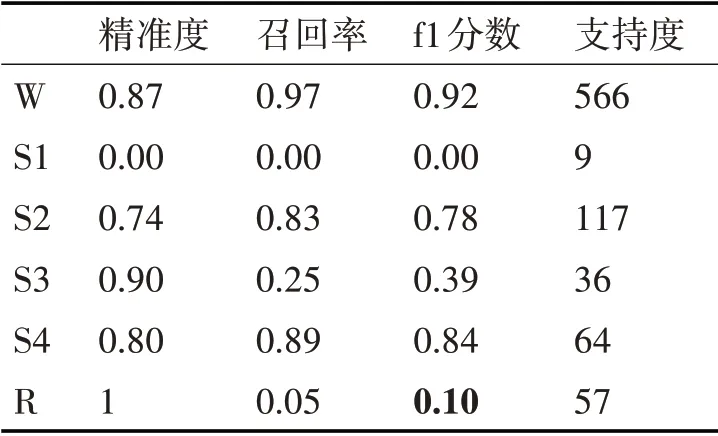
表3 分類結果

測試集共849幀數據，其中R 和S3時期有著較高的準確率，但是召回率較低；S1 時期召回率為0，所以準確率也為0；W、S2、S4 時期都有著較高的召回率和準確率。測試集總體準曲率達到一個較高的水平。

5 結語

受檢者通常需要整晚采集EEG 信號，數據量大，依賴人工逐幀識別進行分期的方法主觀意識強，工作效率低，并且需要較多經驗積累才能準確判斷。利用機器學習的原理，通過特征提取和SVM模型處理睡眠分期任務可以大大提高了工作效率，和準確率。本文完成了利用小波變換的方法對EEG信號進行去噪處理，通過與二階巴特沃斯帶通濾波相比較可以發現此方法去噪平滑效果更好；小波包分解則可以提取出EEG 中的幾種節律波并計算出相應能量值；再計算排列熵和樣本熵以更好地反映EEG 的非線性特征；利用SVM 分類模型得出了分類結果相比于組合KNN分類器提高了2%。