基于BRDPSO 算法的織物表面瑕疵檢測*

張家瑋 李岳陽 羅海馳

（1.江南大學江蘇省模式識別與計算智能工程實驗室 無錫 214122）（2.江南大學輕工過程先進控制教育部重點實驗室 無錫 214122）

1 引言

紡織工業是我國歷史悠久的傳統產業，也是中國工業化進程中的支柱性產業［1］。但在織物的生產過程中，表面瑕疵是最容易出現的質量問題之一。目前，部分企業仍選擇傳統的人工目測法，這種方法易受主觀因素影響，不僅檢測速度慢，準確率也不能達到企業標準。隨著市場對產品要求的不斷提高，大部分企業都急需尋找一種效率更高的瑕疵檢測方法。

常用的織物瑕疵檢測算法過程主要包括圖像預處理、圖像特征提取和分類器分類三個部分，其中圖像特征提取和分類器的模型構建是關鍵的步驟。許多文獻已經表明，特征并非越多越好，冗余和不相關的特征會嚴重影響瑕疵檢測的精度和效率。因此使用離散粒子群算法（BPSO）、主成分分析（PCA）等方法從初始特征空間提取出有效特征的同時又能為后續識別工作降低計算復雜度，提高瑕疵檢測的實時性［2～3］。另外也有大量的研究證明，設置錯誤的參數會導致分類器性能大幅降低，因此使用；量子粒子群算法（QPSO）等對分類器的參數進行優化是提高瑕疵識別準確率的有效途徑之一［4］。

對于特征提取和分類器模型構建，不少學者使用兩步操作的方法，即先使用BPSO 算法或者PCA算法對特征向量進行降維處理，減少特征維度，再使用PSO 算法或遺傳算法（GA）優化分類器模型參數［5］。但這會浪費大量的訓練時間，同時特征選擇和分類器模型參數尋優這兩者之間不是獨立的，而是相互影響和相互聯系的，特征選擇與參數尋優同步進行可以更好地檢測出瑕疵圖像［6］。

因此，本文提出二進制隨機漂移粒子群（BRDPSO）算法，并將此算法結合隨機森林（RF）分類器實現同步特征選擇與參數優化，以保證分類器檢測的實時性、準確性與可靠性。同時將所提出的BRDPSO-RF 算法應用在織物表面瑕疵檢測方面，實驗證明了算法的有效性。

2 二進制隨機漂移粒子群算法

2.1 粒子群優化算法

粒子群優化算法（Particle Swarm Optimization，PSO）是1995 年由Eberhart 和Kennedy 等提出的一種源于對鳥群捕食行為進行模擬的算法［7］。優化問題的解被稱為搜索空間，而搜索空間中的每一只鳥，被稱為“粒子”。每個粒子都對應一個適應值。在迭代的時候，這些粒子通過“自我認知”與“社會認知”追尋群體中的最優粒子以得到問題的最優解。

2.2 隨機漂移粒子群優化算法

隨機漂移粒子群算法（Random Drift Particle Swarm Optimization，RDPSO）是由Jun Sun 等提出的一種PSO變體，其靈感來自放置在外部電場中的金屬導體中的自由電子模型［8］。通過自由電子模型可以知道，電子具有無規則隨機熱運動與定向漂移運動，這兩者運動引導電子到外部電場中具有最小勢能的位置［9］。假如將電場中潛在的勢能函數視為優化問題的目標函數，電子的位置視為問題的一種解決方案，那么電子的移動吸引過程便如同優化算法求解最優解的進化過程［10］。在RDPSO 算法中，電子被視為“粒子”。因而粒子的更新方程式：

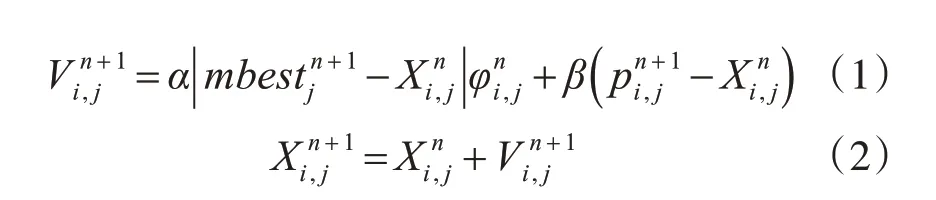
所有粒子個體最好位置的平均值mbest的更新方程如下：

式中：N是粒子群中的粒子數量，Pbest是粒子的個體最好位置。

吸引子pi，j的更新方程如下：

式中：Gbest是所有粒子的全局最好位置，是服從均勻隨機分布的隨機數。

本文為了解決實際問題中的離散空間優化問題將二進制編碼引入RDPSO 算法中，提出了二進制隨機漂移粒子群算法（Binary Random Drift Particle Swarm Optimization，BRDPSO）。

2.3 二進制隨機漂移粒子群算法

在BRDPSO 算法中，粒子包含兩個部分，即隨機森林待優化參數部分和特征掩碼部分，如圖1 所示，粒子前5 位十進制數表示的K1～K5分別代表隨機森林需要優化的5 個參數，后n 位二進制串表示特征掩碼，“1”表示被選中，“0”表示未被選中，Fn值由特征向量維數決定。

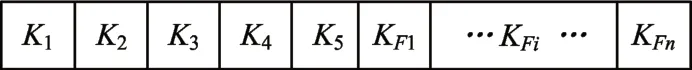
圖1 粒子結構圖

BRDPSO算法的適應度函數Fit可表示為

式中：Accuracy是隨機森林檢測的準確率；ones是BRDPSO 算法選擇的特征數；all代表原始的特征向量維數；wa是準確率權重；wf是特征子集權重，兩者滿足下面的關系：

在BRDPSO 算法中，十進制參數部分的更新方式同RDPSO 算法，而二進制位串部分采用新的更新方式。

平均最好位置mbest的二進制位串部分的求解方法如圖2所示，假設現共有4個粒子，每個粒子有8 位二進制位串，根據這4 個粒子個體最好位置Pbest，通過統計群體中粒子二進制位串編碼的每一位出現0，1 的概率大小，出現0 的次數多，則mbest對應的為0；反之，則為1；當對應位出現的0和1 次數一樣的時候，隨機選擇為0 或者為1［11］。比如，圖2 中4 個粒子個體最好位置Pbesti的第5位和第8位分別有兩個1和兩個0，所以mbest的對應位是隨機產生的。在后續描述BRDPSO 算法中，將平均最好位置mbest的二進制位串部分的求解函數記為Get_mbest(Pbest)。

圖2 mbest 的二進制位串部分的求解方法

第i個粒子的吸引子Pi的二進制位串部份的更新方式類似于遺傳算法中的交叉操作，可以使用單點交叉或多點交叉。在本文中使用的是兩點交叉，更新方式如圖3所示。

圖3 Pi 的二進制位串部份的更新方式

假設Pbesti和Gbest均由8 位二進制串組成。首先隨機將Pbesti和Gbest分為3部分。要求每一部分至少有2 位二進制串，且最多不超過3 位。再通過交叉操作得到pi1和pi2兩個子代，其中，pi1的前3 位來自Pbesti，第3～5 位來自Gbest，最后2 位來自Pbesti；pi2的前3 位來自Gbest，第3～5 位來自Pbesti，最后2 位來自Gbest。最后隨機選擇pi1或pi2作為第i個粒子的吸引子pi的二進制位串部份。在后續描述BRDPSO 算法中將pi的二進制位串部份的求解函數記為Get_p(Pbesti，Gbest)。

在BRDPSO 算法的二進制位串部分，每一個粒子的位置都被限定為0 或1。而0 或1 的位置選擇則由粒子速度決定。此時速度不再表示位置變化的大小，它反映的是該粒子在某一維取1 的概率。因此，由式（1）更新速度得到后，需要通過轉換函數限制概率值在［0，1］之間，本文采用sigmoid函數，即：

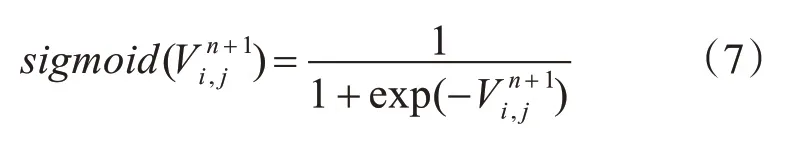
故二進制粒子位串部分粒子位置更新公式如下：

式中：rand()是在（0，1）區間上服從均勻分布的隨機數。

3 實驗過程

本文提出的基于BRDPSO-RF 算法的織物表面瑕疵檢測，其具體流程描述如下。

1）對獲取到的全部織物圖像進行預處理，包括圖像灰度化、中值濾波和同態濾波，以達到圖像增強和去除噪聲的效果；

2）對預處理后的圖像應用基于紋理特征的方法（包括灰度梯度共生矩陣、灰度共生矩陣和局部二值模式LBP）提取特征，得到原始特征數據集；

3）將原始特征數據集隨機劃分為訓練集數據和測試集數據；

4）構造二進制隨機漂移粒子群-隨機森林（BRDPSO-RF）模型，利用訓練集訓練模型，以得出最優特征子集和最佳隨機森林RF分類器參數；

5）根據步驟4）得到的最優特征子集和最佳隨機森林RF 分類器參數，構建新的BRDPSO-RF 模型，對測試集進行瑕疵檢測。

3.1 圖像預處理

實驗中所用的織物均由文獻［12］作者提供，織物的圖像大小均為256×256 像素，色織物的花色背景包括方格紋、星形紋和點紋，瑕疵類型包括斷頭疵、破洞、粗細不同的污漬等。圖4 所示的是其中具有代表性的瑕疵圖像。

圖4 原始圖像

本文的算法只基于圖像的灰度信息，所以先將彩色圖像灰度化。然后使用中值濾波方法去除圖像噪聲，同時保護圖像的邊緣信息。最后使用同態濾波方法減小光照不均的影響，并達到增強圖像對比度和細節的目的。預處理后的圖像如圖5所示。

圖5 預處理后的圖像

3.2 特征提取

本文使用灰度梯度共生矩陣、灰度共生矩陣和LBP提取圖像的紋理特征。

灰度梯度共生矩陣（gray-gradient co-occurrence matrix，GGCM）反映一幅圖像各像素點的灰度和梯度的關系，圖像的灰度是其構成的基礎，而梯度則是構成圖像邊緣輪廓的主要元素，將二者結合起來使用，能夠很好地表征圖像的紋理特征［13］。本實驗選取出了灰度梯度共生矩陣中15 個常用的統計特性，用來描述灰度圖像紋理特征。

1973 年Haralick［14］等提出了用灰度共生矩陣（Gray-level co-occurrence matrix，GLCM）來描述紋理特征。本實驗選取對比度、相異性、同質性、相關度、能量和ASM這6 個特征量來表示紋理特征。選取方式為：在θ(0?，45?，90?，135?)這4 個方向計算灰度共生矩陣，并得到了4組6維特征向量，通過求平均值得到了最后的唯一一組6 維特征向量用以表示基于灰度共生矩陣提取的紋理特征向量。

局部二值模式LBP（Local Binary Patterns，LBP）是由Ojala提出的一種基于灰度描述圖像紋理特征的不相關算子，它通過描述圖像任意一點與其周圍點的灰度值大小關系來表征圖像的局部紋理特征［15］。本實驗使用旋轉不變LBP 提取了256 維紋理特征向量。

3.3 同步特征選擇與參數優化過程

第一步：初始化粒子群，假設粒子的數量為N，維度（搜索空間）為D，并將當前粒子位置賦給粒子個體最好位置，即，其中i=1，2，…，N。

第二步：根據上面式（3）計算平均最好位置mbestj的隨機森林模型參數部分的值，由Get_mbest(Pbest)得到二進制位串部分的值。

第三步：根據式（5）計算每個粒子的適應度函數值。

第四步：粒子個體最優位置更新方式如下：

根據式（5）的適應度函數計算方法，準確率越高越好，選取的特征數量越少越好，因此適應值越大越好。

粒子全局最優位置是所有粒子個體最優位置的最佳值，其更新方式如下：

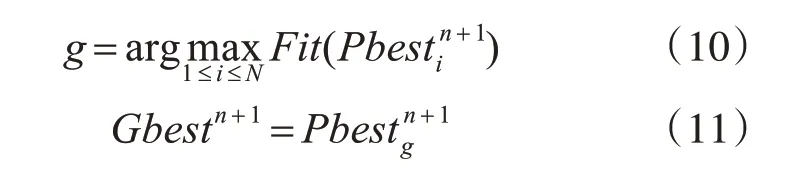
式中：g為所有粒子個體最優位置的最佳值所對應的粒子編號。

第五步：根據式（4）計算吸引子pi的隨機森林模型參數部分的值，并由Get_p(Pbesti，Gbest)計算pi的二進制位串部分的值。

第六步：根據式（1）更新粒子的速度。

第七步：粒子位置的隨機森林模型參數部分的值根據式（2）更新，并根據式（8）更新粒子位置的二進制位串部分的值。

第八步：重復第二步～第七步，直至達到最大迭代次數，得到最終的Gbest。訓練完成后，Gbest的前5 維為最佳的隨機森林參數組合，后n維是最優特征子集，其中“1”表示選擇此特征，“0”表示不選此特征；

第九步：將挑選出的特征向量作為新的特征數據集，同時采用優化后的隨機森林參數，構造BRDPSO-RF 模型，對測試集進行織物表面瑕疵檢測，輸出最終的準確率、漏檢率和運行時間。

4 實驗結果分析

4.1 評價指標

在織物瑕疵檢測中，瑕疵檢測的準確程度和檢測算法的實時性是非常重要的指標。所以本文選取檢測準確率（ACC）、漏檢率（Miss）以及檢測時間（Time）來衡量算法的有效性。ACC和Miss的計算公式如下：

式中：TP代表正確檢測到的無瑕疵樣本的數量，TN代表正確檢測到的有瑕疵樣本的數量，FP代表把有瑕疵樣本檢測為無瑕疵的數量，P代表無瑕疵樣本的全部數量，N代表有瑕疵樣本的全部數量。

4.2 實驗結果及分析

算法采用Python 語言實現，開發環境為Jupyter Notebook，運行環境為Windows 10。樣本圖像是文獻［12］作者提供的75張大小均為256×256 像素的圖像，其中花色背景有三種，分別是方格紋、星形紋和點紋；瑕疵類型有5 種，分別是斷頭疵、破洞、粗細不同的污漬、跳花以及打結。本文先使用重疊的方式對樣本圖像進行分割，并將分割后得到的大小為64×64 像素的小圖像作為最終樣本數據。

本文粒子群的參數設置如表1所示。

表1 粒子群的參數設置

表1 中的熱系數α和漂移系數β分別滿足如下更新方程式：

式中：T是最大迭代次數，t是當前迭代次數；α1和α0分別是α的最大值和最小值；β1和β0分別是β的最大值和最小值。

RF分類器的參數范圍設置如表2所示。

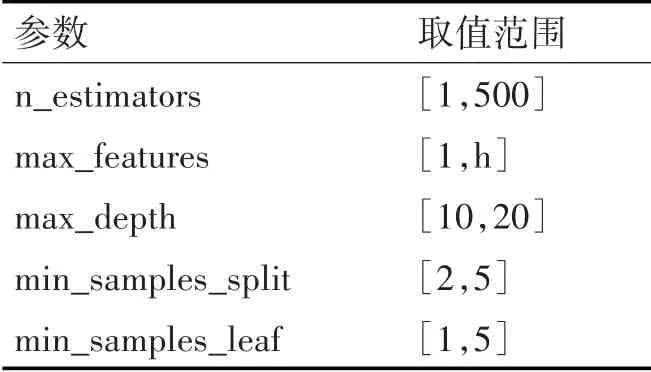
表2 RF分類器的參數取值范圍設置

式中：h代表每次迭代挑選出的特征向量數目。

實驗中取wa=0.9 ，并將本文提出的BRDPSO-RF模型與未進行特征選擇，未進行參數優化的RF 模型；只進行特征選擇，未進行參數優化的BRDPSO-RF1 模型；采用全部特征，只進行參數優化的RDPSO-RF模型；分開進行特征選擇和參數優化的BRDPSO-RF2 模型以及PCA-RF 模型進行對比。表3 示出了在不同背景下，不同模型在5 種類型瑕疵檢測上的結果對比。

從表3 中可以看出，本文提出的BRDPSO-RF模型在準確率和漏檢率方面更優于其他模型。在平均準確率上提高了2.86%～10.27%，其中在瑕疵類型為污漬的圖像檢測上更是將準確率提升到了96.91%；在漏檢率上減少了0.49%～13.26%。從運行時間這方面來看，只進行特征挑選的BRDPSORF1模型更優于其他模型，但是運行時間不止與模型本身有關，還與隨機森林分類器的參數和CPU的使用情況相關。因而綜合來看，從檢測的準確率，漏檢率，特征向量選擇能力以及運行效率等方面綜合考慮，本文提出的BRDPSO-RF 模型均優于以上提及的模型。

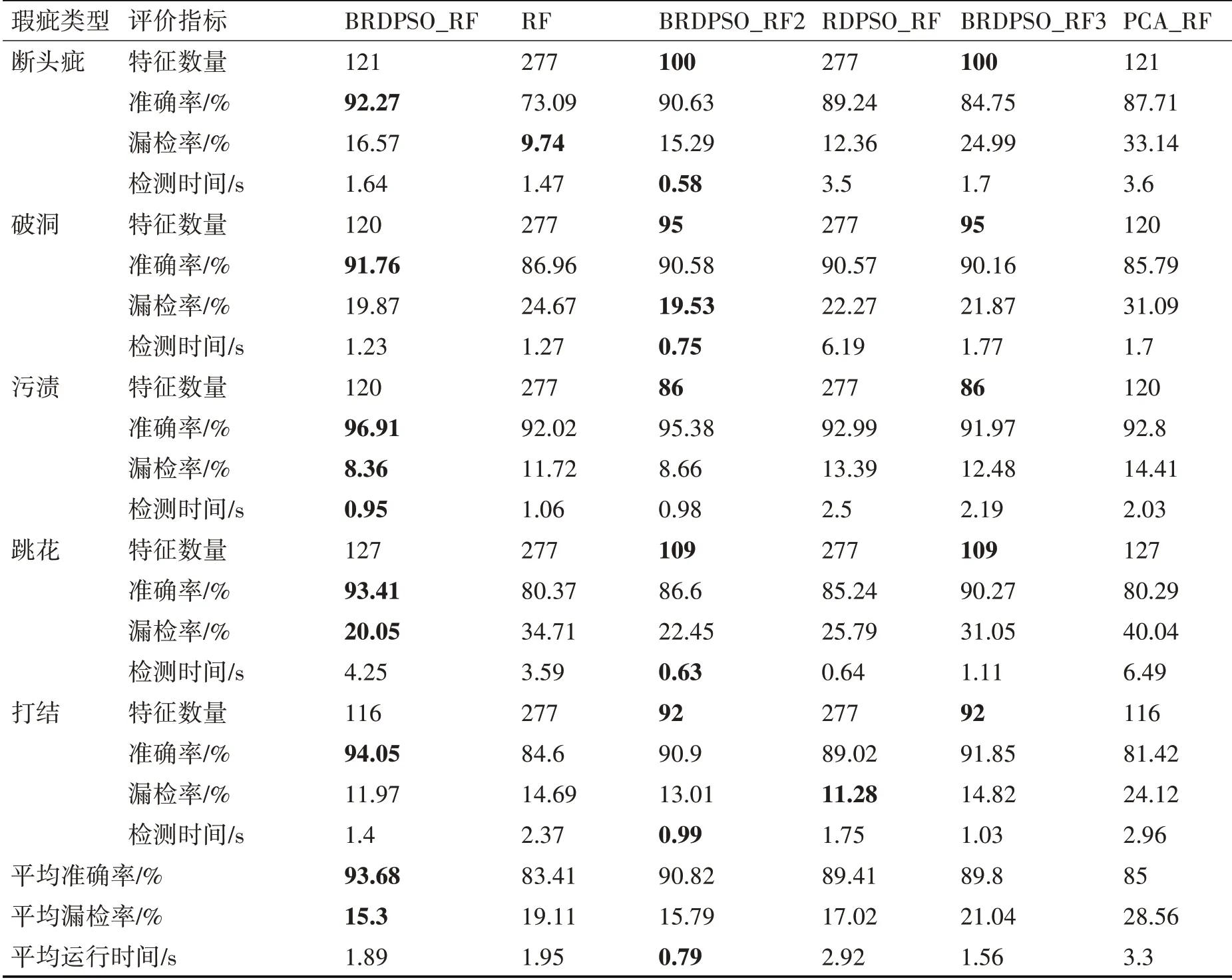
表3 不同模型在5種類型瑕疵檢測上的結果對比

5 結語

本文從同步特征選擇與參數優化的角度出發，創新性地提出了二進制隨機漂移粒子群（BRDPSO）算法，并將該算法與隨機森林算法相結合，構造BRDPSO-RF 模型，然后將該模型應用于織物表面瑕疵檢測中。文中詳細地給出了BRDPSO 算法的迭代方程，并結合隨機森林（RF）算法給出了解決織物表面瑕疵檢測問題的步驟。最后，通過與單獨優化方法、分開優化方法和未優化方法進行對比實驗，證明本文提出的同步特征選擇與參數優化BRDPSO-RF 模型可以去掉冗余的特征，減少特征數量，從而達到減少計算量，保證在實際使用時系統檢測瑕疵的實時性要求，并且具有最優的檢測準確率和漏檢率。