有限厚度模型校準二維MoS2 的Bimodal-AFM 楊氏模量測量1)

陳 珊 * 彭金峰 *, 黃 樂 曾 辛 ** 李立豪 * 何文遠 * 鄭學軍 *

* (湘潭大學機械工程學院,湖南湘潭 411105)

? (湘潭宏大真空技術股份有限公司,湖南湘潭 411104)

** (湖南威勝電氣有限公司,湖南湘潭 411199)

引言

自2004 年首次使用機械剝離法制備出單層石墨烯以來[1],石墨烯和過渡金屬硫族化合物(TMDs)等層狀二維材料,因具有特殊物化性質和廣闊應用前景而受到人們廣泛關注[2].其中,二維二硫化鉬(MoS2)是一種被廣泛研究的典型TMDs 層狀結構材料,在納米摩擦、微電子、儲氫、催化劑、太陽能電池和固體潤滑劑等方面具備巨大的應用潛力[3-4].MoS2大規模應用直接或間接地取決于其力學特性[5],因此研究二維MoS2材料的力學性能和界面力學問題,是材料從實驗室走向具體應用不可或缺的重要步驟.力學特性不僅決定了器件結構和制備工藝,更影響著器件的性能、穩定性和使用壽命[6].此外,力學特性也主導了二維材料在外界作用下的力學響應,對微納尺度下應變調控具有指導意義.

隨著越來越多的二維材料被發現,對其力學性能和相應力學行為的系統研究卻相對滯后.受限于二維結構和原子級厚度特征,發展精細力學表征和測量技術一直是研究重點和難點.現有二維材料彈性模量的測量方法主要有:納米壓痕法[7]、鼓泡法[8]、原位納米力學測試法[9]和雙模原子力顯微鏡(Bimodal-AFM)法[10-11].納米壓痕法是用原子力顯微鏡(AFM)探針下壓懸浮于預制孔上的二維材料,并分析連續加載條件下的力-位移曲線[8].然而,該方法需要AFM 探針與二維懸浮膜中心精確對準,稍有偏差就會導致較大誤差;并且樣品難以轉移到指定的圓孔上,因此通過這種測試方法得到二維材料的力學性能結果不確定性偏大.此外,二維材料通常直接沉積在襯底上并非處于懸浮狀態,從這種懸浮膜上測量出的力學性能參數并不直接適用于器件結構.鼓泡法將二維材料轉移至帶孔基底上,然后在樣品一側利用液壓或氣壓加載裝置施加載荷,最后記錄不同載荷下的撓度,即可得到二維材料的載荷-撓度曲線,進而計算出彈性模量和殘余應力[9].但這種方法制樣困難,且加載不連續.基于掃描電子顯微鏡(SEM)的原位納米力學系統,可以對二維材料進行高分辨原位拉伸/壓縮實驗[10],獲得彈性模量、屈服極限及破壞極限等重要力學參數,但在測試過程中電子束可能會造成樣品結構破壞.Bimodal-AFM 中的振幅調制-頻率調制模式是高效測量材料和界面納米力學特性的方法,能同時測得樣品表面形貌和納米力學特性,提供包括楊氏模量、壓痕深度等在內的彈性信息,且不會限制成像采集速率[11].Bimodal-AFM 已用于二維材料的力學性能測量,如Si/SiO2基底上的單層MoS2納米片和浸泡在液體中的雙分子層脂質薄膜[11-12].然而,在Bimodal-AFM 測量中剛性襯底對納米材料楊氏模量的影響不可忽略,會導致對實際值的高估[13-14].Gisbert 和Garcia[12]采用有限厚度模型校準了襯底效應來獲得真實楊氏模量分布圖,但目前在文獻中仍鮮有報道直接證明襯底效應的假象和驗證Gisbert 方法的有效性.

本文采用二維材料力學性能測量新方法—Bimodal-AFM 測量襯底上單/雙層MoS2納米片的楊氏模量值.并基于第一性原理計算單/雙層MoS2的彈性系數和楊氏模量值,通過對比Bimodal-AFM 實驗方法測得和第一性原理計算的楊氏模量結果,驗證Bimodal-AFM 方法測量結果的準確性,以期為低維材料微納米力學性能測試提供借鑒指導[15].

1 實驗設計

1.1 樣品制備

化學氣相沉積法是一種廣泛應用于可控生長二維納米材料的技術.化學氣相沉積法制備二維MoS2納米片裝置如圖1 所示.首先,按照質量比10:1 稱取硫粉(99.5%,阿拉丁)和三氧化鉬(99.95%,阿拉丁)作為前驅體,分別盛放在兩個瓷舟中.雙溫區管式爐的第一溫區放置裝有硫粉的瓷舟,以5 °C/min 的升溫速率加熱到240 °C 并保溫15 min.在管式爐的第二溫區放置裝有三氧化鉬粉末的瓷舟,并將Si/SiO2(300 nm) 襯底反扣在瓷舟上,以25 °C/min 的升溫速率加熱到680 °C 并保溫15 min.在此溫度下,MoO3粉末被硫蒸汽還原,形成具有揮發性的亞氧化物MoOx[16].這些亞氧化物擴散到基底上,與硫蒸汽反應生成MoS2薄膜.在沉積過程中使用高純氬氣作為載流氣體和保護氣體,加熱前先以200 mL/min 的流量通氬氣20 min,以排除反應管中其他雜質氣體,然后通以150 mL/min 流量的氬氣持續到實驗結束,并冷卻到室溫.

圖1 化學氣相沉積法制備MoS2 裝置示意圖Fig.1 Schematic diagram of MoS2 preparation by chemical vapor deposition

1.2 材料表征

用拉曼光譜測試系統(Raman,Invia RM200,UK) 表征樣品振動特性;用場發射掃描電鏡(FESEM,SU5000,Japan)表征樣品形貌和微觀結構;用X 射線光電子能譜儀(XPS,ESCALAB 250 Xi,UK) 表征樣品中元素化學價態;用原子力顯微鏡(AFM,Cypher S,USA)表征樣品表面形貌并且測量楊氏模量.

1.3 Bimodal-AFM

振幅調制-頻率調制模式屬于Bimodal-AFM 的一種模式,其原理如圖2 所示.利用兩個不同頻率的激勵信號來激勵懸臂振動,第一模式中用低頻激勵信號來激勵懸臂振動,采用振幅調制(AM)模式可以得到樣品的表面形貌,從懸臂的偏轉信號中可以提取頻率f1,幅度A1和相位 φ1.第二模式中用高頻激勵信號來激勵懸臂振動,基于頻率調制(FM)用一個小的振幅A2來測量頻移 Δf2,第二模式的反饋通過頻移 Δf2調整頻率使其相位 φ2維持在 π /2[17-18],同時獲得第二模式的共振頻率和振幅,分別反映了樣品的彈性和黏性[19].Bimodal AFM 對彈性模量的測量有著非常寬泛的適用范圍,從1 MPa 到幾百GPa,是一種適用面廣且分辨率高的力學性質表征的新技術.

圖2 Bimodal-AFM 模式原理示意圖Fig.2 Schematic diagram of in Bimodal-AFM mode

振幅調制-頻率調制模式具體設置如下:在探針-樣品距離為500 nm 狀態下,設置第一、第二模態的自由共振振幅電信號為2 V 和25 mV;為保證第一模態相偏移低于90°,然后將第一模態振幅Set Point 設為800 mV.所有樣品掃描頻率為1.5 Hz 以及數據采集像素為256 × 256.單層MoS2的測試區域為5 μm × 5 μm,雙層MoS2的測試區域為11 μm ×11 μm.測試采用硅探針(AC160 TS-R3,Nanoworld,USA),通過熱噪聲法標定探針懸臂梁彈性常數為36.9 N/m[20].實驗環境溫度為25 °C,相對濕度為30%.

1.4 Bimodal-AFM 襯底效應修正理論

由于襯底效應的存在,Bimodal-AFM 測量沉積在襯底上薄膜材料的楊氏模量時,襯底效應一般會導致對薄膜材料實際模量值的高估[13].因此需要考慮修正襯底效應來消除其影響,校準Bimodal-AFM 測量的彈性特性結果.從矩形懸臂梁的彈性梁方程出發,Bimodal-AFM 激勵模態下探針針尖運動可近似描述為[21]

其中,fi,f0i,Qi,ki和Fi是第i個模式下的驅動頻率、自由共振頻率、質量因子、剛度和驅動力.z(t)為懸臂末端的總撓度,z0,z1和z2分別為靜態、第一、第二模態偏轉,Ai為模態i的振幅,φ1為第一模態的相偏移,并且保持第二模態的相偏移 φ2=π/2 不變.為了便于解析表達式的推導,假設A2的值遠小于A1的值,且z0對于A1和A2可忽略.如圖2 所示,Bimodal-AFM 主要觀測值為A1,φ1和f2以及第二模態驅動力F2,可以通過上述實驗結果計算得到楊氏模量.基于方程(1)考慮Virial 定理,則第一、第二模式激勵下有如下關系

對運動方程式(3)和式(4)在一個周期內積分,可以在相互作用力未知的情況下用觀測值表示上述方程

基于Hertz 接觸力學,半徑為R的球體與平坦半無限彈性材料接觸時排斥力為[22]

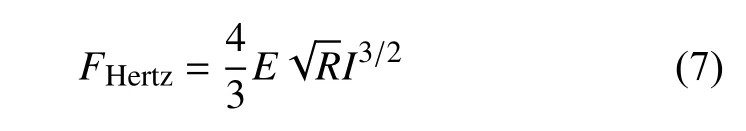
其中，I表示壓痕深度,可設置自由振幅A01改變I大小,在Bimodal-AFM 測試中可直接獲得,在該近似下界面有效楊氏模量Eeff有如下關系[17]

其中,Etip和vtip為針尖的楊氏模量和泊松比,Es和vs為樣品的楊氏模量和泊松比.文獻[12]基于有限厚度模型推導了Bimodal-AFM 襯底效應修正的關于薄膜楊氏模量解析表達式

其中,h為樣品厚度.基于方程(11) 將在下文中對Bimodal-AFM 測量的楊氏模量值進行基底效應校準,相關計算參數有:探針半徑R、探針彈簧常數k1、單層MoS2和雙層MoS2厚度h;并需要調用壓痕深度、第一模態振幅和相偏移通道的數據.

2 實驗結果與分析

2.1 MoS2 及探針的結構和形貌分析

為了表征化學氣相沉積法制備MoS2納米片微觀結構,用拉曼光譜表征振動特性來確定層數,并通過FE-SEM 表征表面形貌.圖3(a),圖3(b)分別為MoS2納米片的拉曼和SEM 圖.圖3(a)中,單層MoS2拉曼光譜在384.78 cm-1和403.89 cm-1處有兩個明顯的振動峰,雙層MoS2拉曼光譜在383.5 cm-1和404.2 cm-1處有兩個明顯的振動峰,對應2H-MoS2的面內振動模式和面外振動模式 A1g[23],這兩種振動模式有強烈的厚度依賴性,前者的頻率隨著厚度增加而降低,后者的頻率則隨著厚度增加而增加[24].和 A1g峰值頻率差 Δw可以用來判別MoS2的層數,圖3(a)藍線和紅線的 Δw分別為19.11 cm-1和20.7 cm-1[25],證明實驗所用的納米片層數為單層和雙層.圖3(b)為MoS2的SEM 形貌,樣品形狀呈現尺寸約為3 μm 的三角形,說明樣品是單晶生長的MoS2.

圖3 MoS2 微觀結構表征Fig.3 Micro-structure characterization of MoS2

在室溫條件下,Bimodal-AFM 測試用探針(AC160 TS-R3,Nano-world,USA)的平均法向彈性常數校準為26 N/m,一階共振頻率為300 kHz,以及二階共振頻率為1.169 MHz.懸臂上鍍有100 nm 厚的鋁膜,用于反射AFM 設備中偏轉傳感器的光線.圖4中SEM 圖像可知,Bimodal-AFM 納米力學實驗用的探針半徑R約為13 nm.

圖4 探針針尖SEM 圖Fig.4 SEM image of probe tip

通過XPS 對MoS2中各元素的化學價態進行了分析,結果如圖5 所示.圖5(a)為MoS2的全譜,從圖中可以明顯看到C1s,O1s,Mo3d 和S2p 的特征峰,圖5(b) 為Mo3d 的高分辨譜,MoS2在229.78 eV 和232.88 eV 處存在一組峰,分別對應于Mo4+3d5/2和Mo4+3d3/2,圖5 (c)為MoS2中S2p 的高分辨譜,MoS2在162.66 eV 和163.87 eV 處存在一組峰,對應于S2-2p3/2和S2-2p1/2,圖5 中各個峰的位置與文獻[26]結果一致.

圖5 MoS2 的XPS 光譜圖Fig.5 The XPS spectra of MoS2

2.2 二維MoS2 的Bimodal-AFM 納米力學圖譜

圖6 為單層MoS2的Bimodal-AFM 納米力學測試結果圖,圖6(a)為化學氣相沉積法制備的MoS2納米片/SiO2(300 nm)樣品AFM 形貌圖,從圖中可得出樣品厚度約為0.8 nm,可以認為該MoS2樣品為單分子層納米片[27],這和圖3(a)中單層MoS2的拉曼光譜測試結果一致.圖6(b),圖6(c)為第一和第二模式的振幅圖,從圖中可以看出第二模式下的振幅A2遠小于第一模式振幅A1,振幅A1穩定在48.5 nm附近,振幅A2在497～ 503 pm 范圍內變動.圖6(d)為第一模式相位圖,用來測量樣品交互剛度,從圖中可以看出相位 φ1小于π /2,且SiO2區 域相位小于MoS2區域相位.圖6(e)為壓痕深度圖,SiO2區域的壓痕深度大于MoS2區域的壓痕深度,圖中最大壓痕深度為25.5 pm.圖6(f)為Bimodal-AFM 模式下直接測得單層MoS2/SiO2樣品的楊氏模量分布圖,可以看出MoS2區域的楊氏模量高于SiO2區域,兩者的模量分布與圖6(a) 形貌分布一致,這表明Bimodal-AFM 測得的原始信號可以定性區分二維材料及襯底的力學性質,圖6(g)為利用有限厚度模型校準后得到的楊氏模量分布圖.從圖6(f)和圖6(g)中提取的單層MoS2楊氏模量直方圖顯示在圖6(h)中,統計得到單層MoS2楊氏模量的直接測量值為56.3±2.76 GPa,經校準后為211.81±23.78 GPa,經過校準后結果與文獻[28]報道數值270±100 GPa 相符合.直接測量值和文獻[28]報道結果相差較大,這可能是襯底效應所導致的.Bimodal-AFM 測試時,在探針正下方的被測區域會產生彈塑性變形,并且材料與探針接觸部分先發生塑性變形,然后在接觸區域的外場通常產生比塑性變形大得多的彈性變形區.當探針下方材料的彈塑性變形均只發生在MoS2薄膜中的時候,實驗得到的結果是薄膜/襯底體系中MoS2膜的力學性能;然而,當探針下方材料的彈性變形區延伸到襯底時,則測試結果反映的是薄膜和襯底的綜合力學性能[29].對于僅厚0.8 nm 的單層MoS2而言,如圖6(e) 所示MoS2區域壓痕深度在15 pm 左右,襯底SiO2的力學性能對測量結果可能存在影響,這時測試結果為單層MoS2和SiO2的綜合力學性能.

圖6 單層MoS2 Bimodal-AFM 實驗結果:(a) AFM 形貌圖;(b)第一模態的振幅;(c)第二模態的振幅;(d)第一模態的相偏移;(e)壓痕深度;(f)校準前楊氏模量分布圖;(g)校準后楊氏模量分布圖;(h)校準前后楊氏模量直方圖Fig.6 Experimental results of Bimodal-AFM for monolayer MoS2:(a)AFM morphology;(b)amplitude of the first mode;(c)amplitude of the second mode;(d)phase shift of the first mode;(e)indentation depth;(f)Young's modulus before calibration;(g)Young's modulus after calibration;(h) histogram of Young's modulus before and after calibration

圖7 為雙層MoS2的Bimodal-AFM 納米力學測試結果圖,從圖7(a)中可得出樣品厚度約為1.5 nm,這和圖3(a)中雙層MoS2的拉曼光譜測試結果一致,可以認為MoS2樣品為雙分子層納米片[27].圖7(b)和圖7(c)為第一和第二模式振幅圖.圖7(d)為第一模式相位圖,φ1小于 π /2 .圖7(e)為壓痕深度圖,SiO2區域的壓痕深度大于MoS2區域的壓痕深度,圖中最大壓痕深度為33.5 pm.圖7(f)和圖7(g)分別為校準前后的楊氏模量分布圖,從圖7(f)和圖7(g)中提取的雙層MoS2楊氏模量直方圖顯示在圖7(h)中,從圖中可以看出實驗測得雙層MoS2的楊氏模量值為219.94±9.72 GPa,校準后的楊氏模量值為205.18±14.09 GPa,經過校準后結果更接近文獻報道數值200±60 GPa[28].可以看出,單層MoS2的楊氏模量高于雙層MoS2,與納米壓痕法測量結果一致[28].

圖7 雙層MoS2 Bimodal-AFM 實驗結果:(a) AFM 形貌圖;(b)第一模態的振幅;(c)第二模態的振幅;(d)第一模態的相偏移;(e)壓痕深度;(f)校準前楊氏模量分布圖;(g)校準后楊氏模量分布圖;(h)校準前后楊氏模量直方圖Fig.7 Experimental results of Bimodal-AFM for bilayer MoS2:(a) AFM morphology;(b) amplitude of the first mode;(c) amplitude of the second mode;(d)phase shift of the first mode;(e) indentation depth;(f) Young's modulus before calibration;(g) Young's modulus after calibration;(h) histogram of Young's modulus before and after calibration

圖7 雙層MoS2 Bimodal-AFM 實驗結果:(a)AFM 形貌圖;(b)第一模態的振幅;(c)第二模態的振幅;(d)第一模態的相偏移;(e)壓痕深度;(f)校準前楊氏模量分布圖;(g)校準后楊氏模量分布圖;(h)校準前后楊氏模量直方圖(續)Fig.7 Experimental results of Bimodal-AFM for bilayer MoS2:(a)AFM morphology;(b)amplitude of the first mode;(c)amplitude of the second mode;(d)phase shift of the first mode;(e)indentation depth;(f)Young's modulus before calibration;(g)Young's modulus after calibration;(h) histogram of Young's modulus before and after calibration (continued)

2.3 第一性原理計算方法與結果

為了驗證有限厚度模型校準后的楊氏模量值準確性,通過VASP 軟件對單/雙層MoS2的力學性能進行了第一性原理計算.在計算中選擇廣義梯度近似的Perdew-Burke-Ernzerhof 泛函描述電子的交換關聯能作用[30].計算過程中單/雙層MoS2采用4 × 6 × 1和4 × 6 × 2 的超胞,自洽迭代次數為200 次,迭代計算自洽精度為1 × 10-7eV,每個原子上的作用力小于0.01 eV/A.體系布里淵區采用3 × 2 × 1 的K 空間網格,平面波截斷能為500 eV.通過對單層/雙層MoS2超胞模型進行結構弛豫,使整個體系的總能量最小,優化后的雙層MoS2的幾何結構如圖8(a)和圖8(b)所示.結構優化后,通過Vaspkit 軟件包生成能量-應變法計算二維材料力學性能的輸入文件及后處理計算結果[31].

二維MoS2為六方晶系,獨立彈性系數為C11,C12,C22和C66,面內應力應變關系可以表示為[32]

基于能量-應變法可以得到Cij(ij=1,2,6)[33]

其中 εij為拉壓應變,E(V0,0) 和E(V,{εi}) 分別是施加應變前后體系的總能量,對應的晶胞體積分別是V0和V,計算得到的單層和雙層MoS2應變-應變能關系如圖8(c)和圖8(e)所示,將結果代入(12)式即可得到單層和雙層的彈性面內剛度矩陣為

圖8 第一性原理計算模型與結果Fig.8 The first-principle calculation model and results

和式(12)對照后可以得到

剛度矩陣和柔度矩陣都是二階張量,滿足坐標轉換關系,據此可以推導出不同方向面內彈性模量[35]

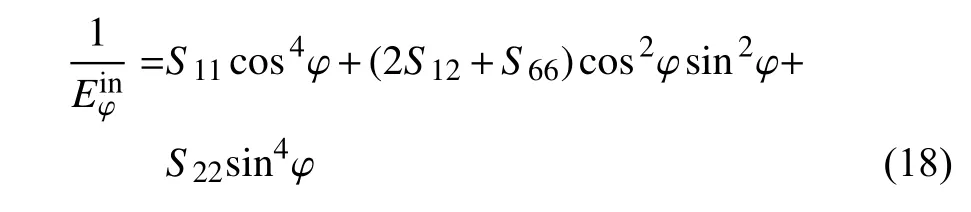
式中Eφ為任意方向面內彈性模量,φ 為方向角度.Sij為柔度矩陣分量,可用剛度矩陣分量表示為

據此,可以得到單/雙層MoS2面內楊氏模量和剪切模量的極圖,結果如圖8(d)和圖8(f)所示.基于第一性原理計算得到單層MoS2剪切模量為50.34±1 N/m,楊氏模量為125.79±1 N/m.雙層MoS2的剪切模量為93.53±4.64 N/m,楊氏模量為236.5±13.5 N/m.為了將第一性原理算得與Bimodal-AFM 測得的楊氏模量值作比較,將計算得到的楊氏模量值除以單/雙層MoS2的理論厚度0.65 和1.3 nm,以轉換成三維楊氏模量[36].經換算后單層MoS2楊氏模量理論計算值為193.5±1 GPa,與經校準后實驗楊氏模量結果(211.81±23.78 GPa) 相差9.45%,但比用SiO2作為標樣校準Bimodal-AFM 測量的楊氏模量結果265±13 GPa[11]更接近理論值.經換算后雙層MoS2楊氏模量理論計算值為181.9±13.5 GPa,與經校準后實驗楊氏模量結果(205.18±14.09 GPa)相差12.79%.這表明,對于單/雙層MoS2,第一性原理計算的楊氏模量結果與校準后實驗楊氏模量結果相當.在引入基底修正模型的基礎上,結合計算和實驗證明Bimodal-AFM 可以準確測量二維材料楊氏模量,驗證了Bimodal-AFM 的有效性和準確性.因此,Bimodal-AFM 力學性能參數測試方法,避免了制備懸空二維材料等繁瑣步驟,實現了二維材料楊氏模量的準確測量,并可以克服傳統方法制樣困難、加載周期長、載荷加載不連續等不足,為程序化測試二維薄膜材料的力學性能提供了可靠實驗基礎,擴展了納米尺度下的精細力學測量技術.

3 結論

彈性模量是二維材料的基本力學特性參數之一,對其器件應用及應變調控有重要影響,因此精確測量二維材料彈性模量十分重要.借助Bimodal-AFM 的振幅調制-頻率調制模式,測量了SiO2基底上生長的單層和雙層MoS2楊氏模量.利用有限厚度模型校準了實驗測得的楊氏模量值,得到了與基于第一性原理能量-應變法算得的楊氏模量值相當的結果,驗證了Gisbert 方法的有效性.Bimodal-AFM 是測量二維材料力學特性的高效方法,可以同時采集樣品的形貌、力學性能,且不會對成像采集速率造成額外的限制,豐富了納米尺度力學特性表征手段.