Nb3Sn 超導線圈力學性能精確分析的雙向均質(zhì)化方法1)

何 安 * 李健博 * 薛 存

* (長安大學理學院,西安 710064)

? (西北工業(yè)大學力學與土木建筑學院,西安 710072)

引言

大科學裝置、未來能源變革性發(fā)展、先進醫(yī)用設備等重大需求牽引下,對磁場強度的要求不斷提高.得益于超導體的強大載流能力(超導載流能力是銅的100 倍以上),高場超導磁體是科學儀器、醫(yī)療、工業(yè)加工、電力裝備和國防特種裝備的核心技術.高磁場的超導磁體伴隨著高電流密度,因此磁體會受到很大的洛倫茲力作用.大規(guī)模的超導磁體主要是由復合材料結(jié)構(gòu)的超導線材或帶材繞制加工裝配而成,在運行過程中較大的電磁力可能會導致磁體產(chǎn)生塑性變形或者局部的機械破壞[1].超導磁體的電磁性能以及運轉(zhuǎn)穩(wěn)定性甚至失超均和磁體的力學變形密切相關,因此準確分析磁體運行時的應力/應變場至關重要[2-4].為了提高超導材料的力學性能,過去的幾十年間,大量的實驗和理論研究了不同形狀和磁化過程中簡單結(jié)構(gòu)超導材料的磁彈性行為.1993 年Ikuta 等[5]首次觀測到了Bi 系單晶超導體中磁通釘扎引起的磁致伸縮行為.Johansen[6-7]根據(jù)臨界態(tài)模型理論研究了長方形和圓柱形塊狀超導體的磁彈性行為,接著根據(jù)Bean 模型和場相關的臨界態(tài)模型Yong 等[8-9]探討了塊狀超導體的斷裂問題[10].另外考慮退磁效應,超導薄帶和圓盤的磁彈性行為也被廣泛報道[11-13].

Nb3Sn 超導材料因其良好的超導性能而被廣泛應用于超導磁體線圈中,但是Nb3Sn 是典型的脆性材料,當對其施加約0.5%的拉伸應變時,就可能會發(fā)生力學失效行為.不僅如此,Nb3Sn 的超導性能對其所處的應力-應變狀態(tài)很敏感,其臨界電流密度會隨著施加應變的增大而迅速減小,并且當所處磁場越強時,臨界電流的退化行為越顯著[14-16].對于理論分析力學變形對超導宏觀臨界性能的影響,楊緒佳等[17]建立從微觀晶格結(jié)構(gòu)到宏觀Nb3Sn 復合超導線的多尺度模型,研究了Nb3Sn 復合超導體臨界性能的力學應變效應.為了保證Nb3Sn 超導磁體線圈安全穩(wěn)定運行,精確預測超導線圈的力學行為具有重要的科學意義.由于高場超導磁體結(jié)構(gòu)復雜,大量的研究工作致力于分析超導磁體線圈的力學性能[18-22],Boso 等[23-25]利用均質(zhì)化方法,考慮 Nb3Sn 超導股線的微觀結(jié)構(gòu)的有限元模型,研究了 Nb3Sn 超導線從制備到工作溫度下所產(chǎn)生的熱應變和等效力學性質(zhì).Zhu 等[26]和 Jia 等[27]先后利用離散單元法,分別建立了二維和三維的離散元模型,研究了 CICC 超導電纜在橫向載荷作用下股線間的接觸問題.Jing等[28]采用復合材料細觀力學中的 Mori-Tanaka 方法建立了考慮絞鈕效應的理論模型.該模型中將連續(xù)的超導芯絲束等效為無限多個取向不同的薄片,分析了超導股線在熱應力和外加荷載作用下芯絲軸向的力學行為和臨界電流的分布情況.Liu 等[29]采用變化局部坐標系下的離散單元方法模擬表征了絞紐的Nb3Sn 股線的力學行為.

由于超導磁體處于強磁場和大電流環(huán)境下,需要考慮電磁場對超導線圈的作用,許多研究者對超導磁體線圈在電磁體力作用下的力學行為展開了研究[30-31],Guan 等[32-33]使用有限元法計算了超導磁體的電磁應力.Wu 等[34-35]建立了超導離子源FECR的六極磁體以及裝配結(jié)構(gòu)的三維有限元模型,分析了大型超導磁體模型的電磁、力、熱多場下的力學行為.Zhang 等[36]建立了超導螺線管詳細有限元模型,采用均質(zhì)化方法分析了線圈超導線直徑變化引起的磁體應力變化.采用有限元均質(zhì)化模型,文獻[37]研究了含36 根MgB2芯絲的超導線繞制的MRI 超導磁體在電磁體力和熱應力作用下的力學行為.

然而目前為止大多數(shù)針對超導線圈力學行為的理論研究僅僅將超導磁體作為各向異性均質(zhì)化模型進行處理,得到的是超導線圈的平均應力-應變場,很難反映超導線圈內(nèi)部各材料實際的應力-應變規(guī)律.由于超導磁體線圈按照其實際的復合結(jié)構(gòu)建模計算量巨大,本文提出了一種精度高而且計算代價低的雙向均質(zhì)化建模方法,用來分析Nb3Sn 超導磁體內(nèi)部各材料的應力-應變.與已有單向均質(zhì)化方法相比,改進的方法具有雙向和返回特征,能夠更加精確地描述復合超導線圈結(jié)構(gòu)的精細應力-應變場.本文的內(nèi)容安排如下:首先基于代表性體積單元等效方法,建立超導磁體等效均質(zhì)化有限元模型,將線圈在外加荷載下均質(zhì)化有限元模型與小匝數(shù)真實線圈模型的結(jié)果進行對比,發(fā)現(xiàn)均質(zhì)化模型與真實模型相比誤差較大.本文提出的多尺度分析方法很好地解決了這個問題,為了驗證該方法的有效性和準確性,將線圈匝數(shù)較小時計算的真實結(jié)構(gòu)超導線的應力-應變場與該方法所得的結(jié)果進行對比,兩者最大誤差小于5%,最后基于提出的多尺度計算方法,詳細研究了大尺寸多匝數(shù)的超導線圈不同位置處的應力-應變的變化規(guī)律.

1 等效均質(zhì)化模型的局限性

1.1 均勻化等效參數(shù)計算方法

超導線圈一般是由微米級的超導芯絲復合成毫米級的超導線,再由超導線經(jīng)過一匝一匝、一層一層繞制而成,跨越了多個數(shù)量級,最后形成復雜的復合結(jié)構(gòu)體系.常見的超導線圈如圖1(a)所示,通入環(huán)形電流I0,產(chǎn)生的感應磁場使得線圈受到徑向洛倫茲力作用,圖1(b)表示超導線圈橫截面由1558 根超導線組成,線圈具有很強對稱性和周期性,從橫截面任意選取一個代表性單元如圖1(c)所示.該單元由54 根Nb3Sn 超導芯絲(紅色六邊形)、銅基(淺綠色部分)和環(huán)氧樹脂(最外層的深綠色部分)組成.研究線圈時若要從超導芯絲尺度開始建模,需要消耗大量的計算資源,并且需要大量的計算時間.為了避免大規(guī)模數(shù)值計算,人們提出了均質(zhì)化模型,其主要思想是在結(jié)構(gòu)復雜的區(qū)域中尋找一個代表性體積單元,使得該代表體元具有普遍的適用性,能夠代表該單元所覆蓋區(qū)域的所有材料集合的力學性質(zhì),對于選定的代表體元的性質(zhì)可以通過均勻化方法計算得出.本文要研究的Nb3Sn 超導線線圈是由銅、環(huán)氧樹脂、Nb3Sn 芯絲三種材料組成的復合結(jié)構(gòu).Nb3Sn超導線的性質(zhì)是與其幾何構(gòu)型相關的,其性質(zhì)表現(xiàn)為正交各向異性材料,不能只通過楊氏模量和泊松比這兩個材料參數(shù)來確定.

圖1 超導線圈電磁力示意圖及其代表性體單元Fig.1 Schematic diagram of electromagnetic force and microscopic material composition of superconducting coil

一般材料的彈性本構(gòu)關系可以寫成

這里 σ 為應力張量,ε 為應變張量,D為四階對稱彈性張量.當材料的性質(zhì)在任一點處關于三個正交平面對稱時,該材料就是正交各向異性的.Nb3Sn 超導股線就可以看作是正交各向異性材料.此時,材料常數(shù)從各向異性材料的21 個常數(shù)減少到正交各向異性材料的9 個常數(shù),在這種情況下,材料的線彈性更容易由給出材料的工程常數(shù)及與材料三個主方向的楊氏模量E1,E2,E3;泊松比 ν12,ν13,ν23,ν31,ν21,ν32和剪切模量G12,G13,G23來描述.這些常數(shù)可以給出材料的柔度矩陣,用柔度矩陣表示為

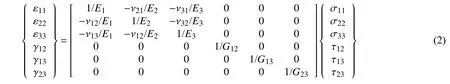
其中 νij和 νji有如下關系

本文目的是確定柔度矩陣中的材料參數(shù),通常的方法是尋找平均場之間的本構(gòu)關系以及與體積平均變量相關的本構(gòu)關系.體積平均變量的關系由“代表性體積單元”確定,為了獲得期望場的體積平均,需要在RVE 上施加一系列試驗性的位移邊界條件進而得到對應方向的平均應力狀態(tài).因此RVE 等效體的本構(gòu)關系可以表示為.正交各向異性材料可以通過有限元方法施加六種單獨的位移邊界條件求解得到C進而得到等效材料參數(shù)

其中,由給定六個單獨的單位應變,可以計算得到在RVE 上施加的位移大小: λi=εijxj,xj表示的是RVE沿著j方向上的長度.六個位移條件

上式的前三種情形為代表性單元施加的單軸應變邊界條件,后三種情形為代表性單元施加的純剪切應變邊界條件.由有限元方法在RVE 積分點上計算得到平均應力,V 代表RVE 的體積,nj是沿著j方向的單位向量分量.一旦得到RVE 在六個位移條件下的平均應力,便可由剛度矩陣計算得到材料的等效參數(shù).

如圖1(c)所示便是本文研究的超導線圈的一個代表性體積單元,此單元包含三種材料組分,最外層的環(huán)氧樹脂邊長為1.4 mm,銅基直徑1.3 mm,Nb3Sn六邊形芯絲邊長0.06 mm.為了消除材料參數(shù)的選取對計算結(jié)果的影響,本文選用了Nb3Sn、銅和環(huán)氧樹脂三種材料的兩組力學參數(shù)如表1 所示,使用RVE 方法計算出超導線圈的兩組等效參數(shù)即工程常數(shù)如表2 所示(其中參數(shù)符號下標數(shù)字1,2 和3 分別對應超導線單元的徑向、軸向和環(huán)向).值得注意的是文中表1 給出的兩組材料參數(shù)中,第一組材料參數(shù)是對應實際工程材料的參數(shù)(見文獻[38-39]).為了進一步驗證所提計算方法的正確性,不是僅適用于特定某種材料,所以除了實際工程材料參數(shù)外,還隨便選取了第二組材料參數(shù)進行驗證.但是在驗證計算方法正確性之后,均采用第一組材料參數(shù)(對應實際工程材料)進行有限元計算和分析.

表1 兩組超導線各材料組分力學參數(shù)Table 1 Mechanical parameters of each material component for two kinds of superconductors

表2 兩組超導線的等效力學參數(shù)Table 2 Equivalent mechanical parameters for two kinds of superconductors

本文在超導線圈結(jié)構(gòu)和復合結(jié)構(gòu)的單根超導線兩個尺度上進行了力學分析,出發(fā)點是單根超導線,其復合結(jié)構(gòu)包括多根超導芯絲、銅基材料和環(huán)氧樹脂,這三種材料的力學屬性(包括力學本構(gòu)及力學參數(shù))仍然建立在宏觀尺度,沒有涉及到晶格和晶粒尺度.每一種材料都認為是宏觀各向同性的,例如對于多晶Nb3Sn 材料,盡管每個晶粒的晶格取向不同,但很多晶粒在宏觀統(tǒng)計上認為是各向同性的,本構(gòu)關系也是各向同性的.以單根超導線的一個扭距長度(大約13 mm)為基礎,采用均質(zhì)化方法得到超導線圈結(jié)構(gòu)的各方向的等效力學參數(shù),論文中表里面的各方向不同等效力學參數(shù)是由于單根超導線復合結(jié)構(gòu)導致的.

1.2 等效均質(zhì)化模型與真實線圈應力-應變結(jié)果對比

得到線圈等效力學參數(shù)后,借助有限元分析軟件ABAQUS,計算超導線圈在施加電磁體力后的應力-應變 (為了方便,本文的線圈計算結(jié)果均僅展示一半線圈結(jié)構(gòu)).首先檢測等效均質(zhì)化模型的準確性,將等效均質(zhì)化模型與真實結(jié)構(gòu)的線圈模型在相同荷載下的應力-應變結(jié)果進行對比分析.如圖2(a)所示為直徑100 mm 的線圈及其橫截面 3 ×3 排布超導線的復合結(jié)構(gòu)模型,圖2(b)是圖2(a)線圈的等效均質(zhì)化模型.由于圓形線圈的對稱結(jié)構(gòu),在半圓線圈的端面施加對稱邊界條件,計算結(jié)果與圓形線圈的結(jié)果相同,圖2(a) 和圖2(b) 兩種模型均采用相同的C3D8R 單元網(wǎng)格,在線圈外側(cè)施加同等大小的壓強荷載.

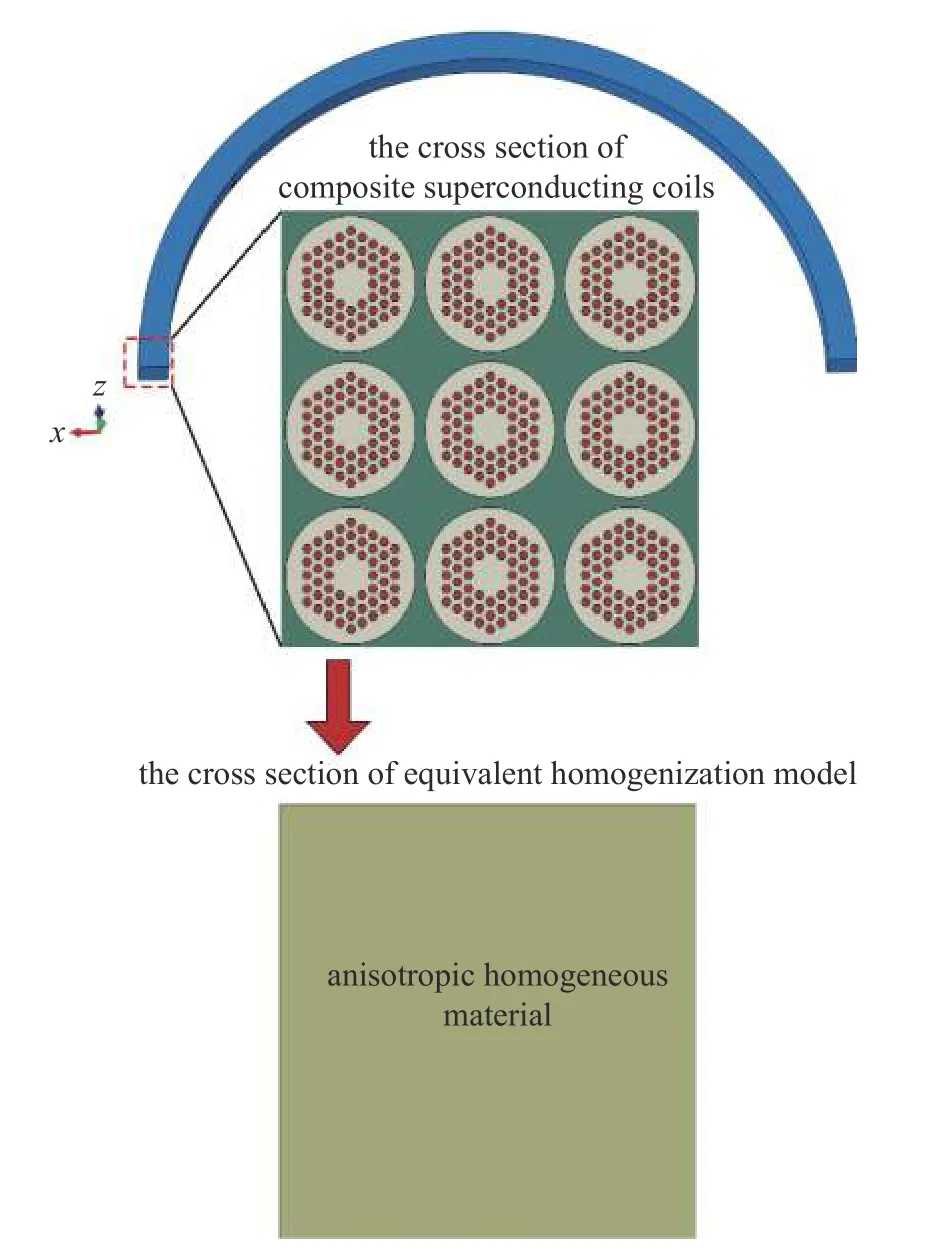
圖2 超導線 3 ×3 排布的復合線圈結(jié)構(gòu)和等效均質(zhì)化模型Fig.2 The actual structure and equivalent homogenization structure of 3×3superconducting coils

圖3 分別給出了超導線 3 ×3 排布的線圈真實結(jié)構(gòu)和等效均質(zhì)化模型用第一組材料參數(shù)計算得到位移、應力和應變結(jié)果.通過圖3(a)的位移場云圖可以看出,相同荷載下兩種結(jié)構(gòu)的位移場吻合較好,數(shù)值相差在1%以內(nèi),分布規(guī)律相同.然而相比位移場結(jié)果,這兩種模型的應力和應變的結(jié)果相差較大.從圖3(b)可以看出等效均質(zhì)化模型的米塞斯應力分布較為均勻,等效均質(zhì)化模型的應力最大值分布于線圈的內(nèi)側(cè).而復合材料線圈結(jié)構(gòu)的應力由材料不同而分層分布,應力的最大值分布于銅基層,兩者的應力最大值相差近30%,最小值相差近60%.從圖3(c)可知兩者的最大主應變數(shù)值相差近27%,說明等效均質(zhì)化模型同樣不能很好地反映出真實結(jié)構(gòu)下線圈各層的應變場情況.由于復合材料中不同材料之間的彈性模量相差較大,等效均質(zhì)化模型計算結(jié)果僅能反映整體結(jié)構(gòu)的一個平均水平,無法評估不同材料的具體應力-應變水平是否達到屈服或者破壞.在對比了芯絲 3 ×3 的線圈模型以后,進一步對比了同一組參數(shù)下的超導線 3 ×5 以及 5 ×5 排布的真實線圈結(jié)構(gòu)和等效均質(zhì)化模型的計算結(jié)果(由于篇幅限制,本文不再展示),得出了均質(zhì)化模型與真實線圈結(jié)構(gòu)應力-應變場相差較大的結(jié)論.

圖3 3 ×3 線圈模型(a)真實結(jié)構(gòu)和(b)等效模型的位移場云圖;(c)真實結(jié)構(gòu)和(d)等效模型的Mises 應力云圖;(e)真實結(jié)構(gòu)和(f)等效模型的最大主應變云圖Fig.3 Displacement distributions of (a) actual structure and (b) equivalent model of 3 ×3 superconducting coils;Mises stress distributions of (c)actual structure and (d) equivalent model;Maximum principal strain distributions of (e) actual structure and (f) equivalent model

因此,要想準確表征Nb3Sn 芯絲、銅基和環(huán)氧樹脂各種材料的應力-應變,需要考慮包含這三種材料組分的精細有限元模型,但是隨著線圈匝數(shù)和層數(shù)的增加,有的大型磁體的芯絲數(shù)量已經(jīng)達到上萬根,這對計算機的建模和計算是艱難的挑戰(zhàn),在上文進行 3 ×5 ,5 ×5 模型對比分析的過程中計算已經(jīng)較為困難.尚且需要一種對計算資源要求低,且計算結(jié)果吻合度較高的方法.

2 多尺度計算方法及其精確性驗證

等效均質(zhì)化模型僅能反映超導線圈位移場,不能表征超導線圈內(nèi)各材料精確的應力-應變分布.針對以上問題,本文對整個線圈采用均質(zhì)化模型,通過提取精細化超導線單元的位移場,提出了一種計算精度高但是代價低的多尺度建模方法,用來計算超導線圈內(nèi)各種材料的應力-應變場.由于等效均勻化模型能較好地反映出真實線圈的位移場,因此在從等效均質(zhì)化模型得到位移場的基礎上,把線圈中間部位約2°轉(zhuǎn)角對應的弧段截取出來作為研究超導線單元如圖4(a)所示.當線圈的直徑較大,在線圈中提取的微小弧段可以近似看成是直超導線長方體超導線單元結(jié)構(gòu).通過分析可知在超導線單元結(jié)構(gòu)的六個面上的每一個結(jié)點都有對應全局坐標系下的三個方向位移的分量.借助ABAQUS 的后處理模塊,將六個面的所有結(jié)點位移導出,將對應的位移場數(shù)據(jù)處理作為新的位移荷載(共18 組),由于提取的超導線單元近似為長方體,因此僅需處理每個面對應法向的位移作為位移場荷載(共6 組).通過分析每個面法向的所有結(jié)點位移數(shù)據(jù),發(fā)現(xiàn)所有結(jié)點的大小差距較小且分布均勻,采取求和取平均的方法即可得到每個面的對應方向的平均位移荷載大小.導入新建的對應尺寸的超導線單元模型(圖4(b))進行分析計算,便可以得出線圈對應部位的各材料的應力-應變分布情況.

圖4 復合超導線圈結(jié)構(gòu)內(nèi)部截取的微弧段和施加等效位移荷載的超導線單元示意圖Fig.4 Schematic diagram of micro segment from the composite superconducting coil and the unit cell with equivalent displacement load

為了驗證此方法對于分析線圈內(nèi)部應力-應變場的準確性,計算了 3 ×3 排布線圈內(nèi)部的真實應力-應變場與施加位移荷載的超導線單元結(jié)果,同時計算了不同材料參數(shù)下的 3 ×3 線圈的對比結(jié)果.圖5(a)和圖5(b)分別展示了線圈內(nèi)部截取的微弧段和施加位移荷載的超導線單元的米塞斯應力云圖,通過對比可以看出,施加位移荷載的超導線單元各處的應力分布和大小與真實線圈對應位置的結(jié)果較為吻合,且可以看出各層材料之間不同的應力分布,由于Nb3Sn 芯絲的彈性模量大于另外兩種材料,因此應力最大值分布于Nb3Sn 芯絲中,兩者應力數(shù)值相差近2%.從線圈內(nèi)的微弧段和施加位移荷載的超導線單元的徑向和軸向應變云圖,可以看到應變的分布基本吻合,數(shù)值相差均在5%以內(nèi).由圖6 的對比結(jié)果來看,盡管第二組材料參數(shù)中銅和Nb3Sn 的彈性模量差距較大,但是應力-應變的對比結(jié)果都較為吻合,因此材料參數(shù)的變化并不影響此方法計算結(jié)果的準確性.

圖5 第一組材料參數(shù)下 3 ×3 線圈內(nèi)部截取的(a)微弧段(實際結(jié)果)和(b)施加位移荷載的超導線單元的Mises 應力云;(c)微弧段和(d)超導線單元的徑向應變云圖;(e)微弧段和(f)超導線單元的軸向應變云圖Fig.5 Mises stress distributions of micro segment from (a) the superconducting coil and (b) the unit cell;radial strain distributions of (c) segment and(d) the unit cell;axial strain distributions of (e) segment and (f) the unit cell for the first set of material parameters

圖6 第二組材料參數(shù)下 3 ×3 超導線圈內(nèi)部截取的(a)微弧段和(b)施加位移荷載的超導線單元的Mises 應力云圖;(c)微弧段和(d)超導線單元的徑向應變云圖;(e)微弧段和(f)超導線單元的軸向應變云圖Fig.6 Mises stress distributions of micro segment from (a) the superconducting coil and (b) the unit cell;radial strain distributions of (c) segment and(d) the unit cell;axial strain distributions of (e) segment and (f) the unit cell for the second set of material parameters

進一步,對比 3 ×5 線圈實際模型與多尺度模型的結(jié)果,如圖7 所示,采用本文提出的方法得到超導線單元的米塞斯應力、徑向應變和軸向應變均與真實線圈的結(jié)果吻合較好.Nb3Sn 芯絲和銅基部分的應力大于環(huán)氧樹脂的數(shù)值,而環(huán)氧樹脂的應變大于Nb3Sn 芯絲和銅基的.

圖7 3 ×5 線圈內(nèi)部截取的(a)微弧段和(b)施加位移荷載的超導線單元的Mises 應力云圖;(c)微弧段和(d)超導線單元的徑向應變云圖;(e)微弧段和(f)超導線單元的軸向應變云圖Fig.7 Mises stress distributions of micro segment from (a) superconducting coils and (b) the unit cell with displacement load;radial strain distributions in (c) micro segment and (d) the unit cell;axial strain distribution in (e) micro segment and (f) the unit cell

在此基礎上圖8 展示了微弧段和超導線單元中不同材料的米塞斯應力分布,由于施加的位移荷載均為各面法向的均勻荷載,在長方體超導線單元中各層材料應力分布具有明顯的對稱性.從圖8 中可以看出環(huán)氧樹脂層區(qū)域米塞斯應力最大值分布于中間部位的邊緣位置,銅基和芯絲層應力最大值分布于材料的左右兩側(cè)較小的區(qū)域,而線圈對應的超導線單元應力受彎曲弧度的影響,體現(xiàn)出應力隨著徑向從內(nèi)向外的遞減趨勢,應力最大值位于超導線單元內(nèi)側(cè).從應力數(shù)值來看,銅層和芯絲層整體應力數(shù)值變化較小,相差不超過1%,并且兩種模型的最大應力數(shù)值基本吻合一致.

圖8 3 ×5 線圈截取(a)微弧段和(b)施加位移荷載的超導線單元內(nèi)環(huán)氧樹脂的Mises 應力云圖;(c)微弧段和(d)超導線單元內(nèi)銅基的Mises 應力云圖;(e)微弧段和(f)超導線單元內(nèi)Nb3Sn 芯絲的Mises 應力云圖Fig.8 Mises stress distributions of epoxy resin in (a) micro segment and (b) the unit cell;cooper matrix in (c) micro segment and (d) the unit cell;Nb3Sn filaments in (e) micro segment and (f) the unit cell

3 電磁體力下超導線圈應力-應變規(guī)律

3.1 超導線圈電磁體力計算

超導磁體在通電運行時,磁體內(nèi)部會受到巨大洛倫茲力的作用.根據(jù)畢奧-薩伐爾定律

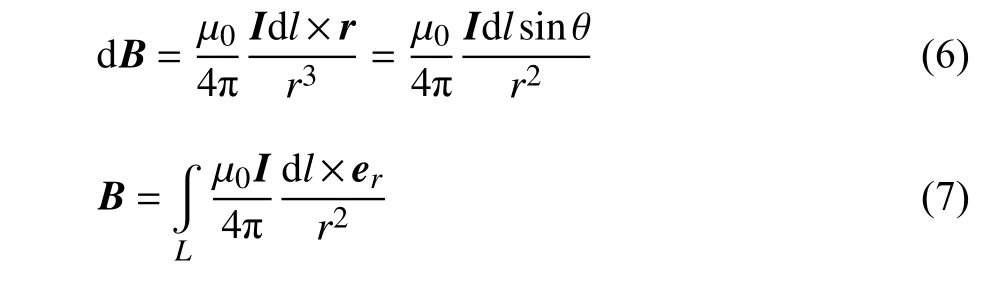
其中,dl是微電流元,L是線圈環(huán)向的路徑,er為電流元指向待求場點的單位向量,μ0為真空磁導率.式(7)和式(8)可以得到環(huán)形超導線圈通電運行下的磁場分布和大小.超導線圈受到的洛倫茲力可以由下面的計算式得到

本文研究的超導磁體具有很強的軸對稱性,在柱坐標系下,磁體受到的洛倫茲力只有徑向分量Fr和軸向分量Fz.圖9 所示為輸入700 A 電流下,超導線圈某個xz截面上的洛倫茲力大小以及方向,箭頭所指為洛倫茲力的方向.可以看到洛倫茲力在線圈的外部區(qū)域較大,在線圈中心位置處較小,線圈的內(nèi)側(cè)表面洛倫茲力最大,洛倫茲力在線圈上下部分呈對稱分布.

圖9 超導線圈xz 截面上電磁體力大小及方向Fig.9 Electromagnetic force distributions in xz cross section of superconducting coil

3.2 超導線圈各層材料應力-應變隨匝數(shù)/層數(shù)變化情況

基于以上雙向均質(zhì)化方法對超導線圈力學性質(zhì)分析的準確性,采用該方法對超導線圈在電磁體力下的應力-應變進行分析,給出不同位置各材料的力學性質(zhì)隨匝數(shù)/層數(shù)的變化規(guī)律.線圈模型中Nb3Sn 超導線沿著徑向排布38 層,沿著軸向排布41 匝,線圈的整體尺寸達到內(nèi)徑167.6 mm,外徑215.75 mm,軸向高60 mm.圖10 給出的是超導線圈橫截面超導線的排布情況,為了簡便計算,選取橫截面中具有代表性的層數(shù)和匝數(shù)進行計算,例如選取線圈的上、中、下三匝(紅色虛線)作為超導線單元提取路徑,沿著z軸選取左、中、右三層(黃色虛線)作為超導線單元提取路徑,其中每條線上的一個點是一個代表性單元.分別計算超導線單元內(nèi)各材料的力學性質(zhì)隨層數(shù)和匝數(shù)變化情況.

圖10 超導線圈橫截面超導線的排布情況及提取超導線單元路徑示意圖Fig.10 Schematic diagram of the location of the unit cells in the superconducting coil

圖11 給出了超導線圈第1,21 和41 匝位置處環(huán)氧樹脂、銅基和Nb3Sn 芯絲的最大主應力隨層數(shù)的變化規(guī)律,從圖11 可知線圈上、下表面處的最大主應力相等(第1 匝和第41 匝的結(jié)果重合).這是由于電磁體力在線圈內(nèi)關于z方向?qū)ΨQ分布導致的,即電磁體力在線圈上下表面處數(shù)值相等且外部的電磁體力數(shù)值高于內(nèi)部,所以線圈上下表面處的最大主應力基本上大于中間處的數(shù)值,在線圈中間第21 匝的端部主應力最大.比較這三種材料的應力值,環(huán)氧樹脂區(qū)域的應力值最小,銅基居中而Nb3Sn 芯絲最大,這是因為環(huán)氧樹脂、銅的彈性模量低于Nb3Sn.另外線圈上下邊界處環(huán)氧樹脂的應力隨著層數(shù)的增加而略微增大但整體變化幅度不大,銅基和芯絲的應力數(shù)值遠高于環(huán)氧樹脂,而銅基和Nb3Sn芯絲的應力隨著層數(shù)的增加而減少,由此可知線圈內(nèi)側(cè)的應力容易達到應力極限從而發(fā)生強度失效.

圖11 超導線圈第1,21 和41 匝的最大主應力隨層數(shù)的變化情況Fig.11 Variations of the maximum principal stress versus layer for the 1st,21st and 41st turn in superconducting coils

圖12 和圖13 展示了線圈第1,21 和41 匝位置處環(huán)氧樹脂、銅基和Nb3Sn 芯絲的徑向和軸向應變隨層數(shù)的變化情況.這三種材料的徑向和軸向應變均為壓應變,第1 和第41 匝的徑向和軸向應變數(shù)值基本重合,體現(xiàn)了電磁體力的對稱性.徑向應變數(shù)值沿著層數(shù)先增大后減小,所以徑向應變在線圈的中間層最大.圖13 展示的三種材料的軸向應變隨著層數(shù)的增加而降低,即軸向應變在線圈內(nèi)側(cè)最大.線圈中間匝數(shù)的軸向應變均高于線圈其他區(qū)域,因此軸向應變在線圈第21 匝最大,在線圈上下表面最小.環(huán)氧樹脂的軸向壓應變在線圈中間達到了1.9%,而銅基和芯絲的軸向壓應變最大僅有0.38%.根據(jù)線圈不同匝數(shù)下的徑向和軸向應變分布情況,徑向應變在線圈的第19 層最大,軸向應變在線圈內(nèi)側(cè)中間匝數(shù)處即第1 層和第21 匝相交處最大,線圈環(huán)氧樹脂區(qū)域的應變相較于其他材料的數(shù)值更大.

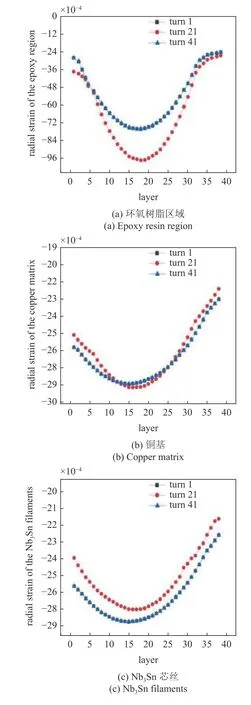
圖12 超導線圈不同匝數(shù)的徑向應變隨層數(shù)的變化情況Fig.12 Variations of radial strain as a function of layer in superconducting coils

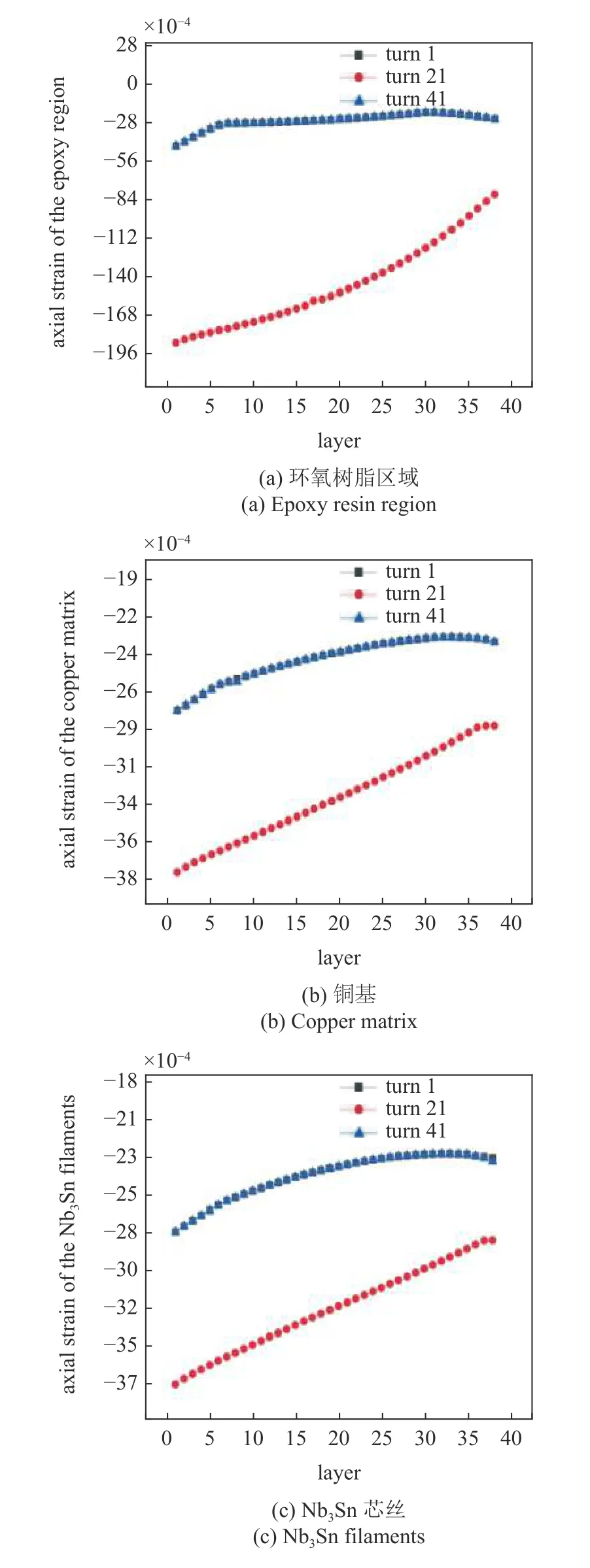
圖13 超導線圈不同匝數(shù)的軸向應變隨層數(shù)的變化情況Fig.13 Variations of axial strain versus layer in superconducting coils

為了分析線圈的力學性質(zhì)沿著z方向的變化情況,圖14 給出了線圈第1,19 和38 層的各材料的最大主應力隨著匝數(shù)的變化情況.這三種材料在線圈內(nèi)側(cè)第1 層的主應力最大,在線圈中間層次之,在線圈外側(cè)最小,這是因為電磁體力在線圈內(nèi)側(cè)最大.最內(nèi)側(cè)和最外側(cè)的應力數(shù)值隨著z軸方向變化不明顯,然而線圈中間層的主應力在中間匝處最小,在上下兩端處最大,且這些應力隨匝數(shù)的變化關于第21 匝呈對稱分布,這是由于電磁體力的對稱性造成的.

圖14 超導線圈不同層數(shù)的最大主應力隨匝數(shù)的變化情況Fig.14 Variations of the maximum principal stress versus turn in superconducting coils

圖15 和圖16 分別展示超導線圈第1,19 和38 層處三種材料的徑向和軸向應變隨著匝數(shù)變化的情況曲線.線圈的徑向和軸向應變均為壓應變且關于第21 匝位置對稱.從圖15 可以看出,超導線圈中間即第19 層的徑向壓應變最大,線圈內(nèi)側(cè)徑向應變次之,線圈外側(cè)應變最小,可以發(fā)現(xiàn)線圈內(nèi)部的徑向應變大于線圈外部,這是由于線圈截面整體是一個受壓變形的狀態(tài),內(nèi)部區(qū)域的變形大于外部的變形,徑向應變隨著匝數(shù)的變化幅度不大,環(huán)氧樹脂區(qū)域的徑向應變數(shù)值高于銅基和芯絲區(qū)域.圖16 給出超導線圈軸向應變隨著匝數(shù)先增大后減小,在線圈中間第21 匝處達到最大值.軸向應變數(shù)值隨著層數(shù)的增加逐層減小,在線圈的內(nèi)層軸向應變最大,軸向應變的這個變化規(guī)律與圖13 一致.相比于銅基和Nb3Sn 芯絲,環(huán)氧樹脂區(qū)域產(chǎn)生的軸向和徑向應變最大.

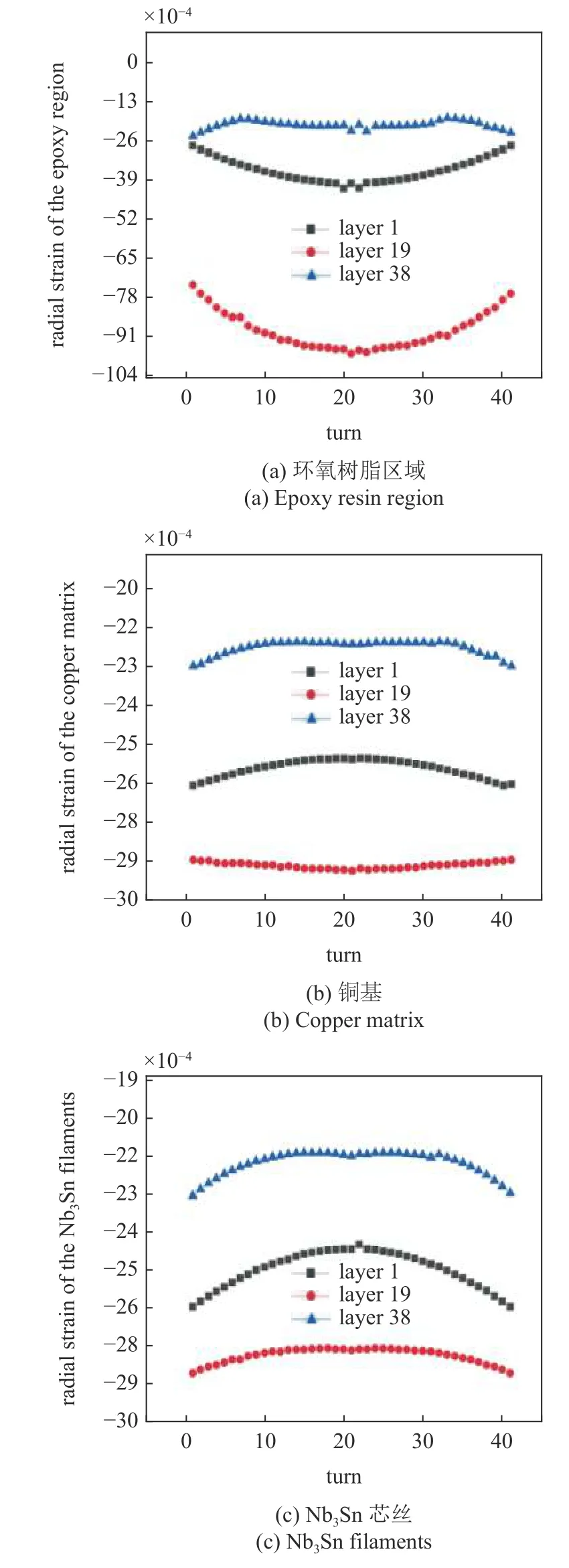
圖15 超導線圈不同層數(shù)的徑向應變隨匝數(shù)的變化情況Fig.15 Variations of radial strain as a function of turn in superconducting coils

圖16 超導線圈不同層數(shù)的軸向應變隨匝數(shù)的變化情況Fig.16 Variations of axial strain versus turn in superconducting coils

4 總結(jié)

針對復雜的多尺度超導線圈結(jié)構(gòu),采用等效均質(zhì)化模型計算的超導線圈應力-應變與實際結(jié)果存在較大差距,等效均質(zhì)化模型僅能反應超導線圈整體的平均應力-應變情況.為了改進均質(zhì)化模型,提高精確性,本文提出雙向均質(zhì)化方法分析超導線圈在電磁力作用下內(nèi)部各材料的應力-應變規(guī)律.相比均質(zhì)化模型,本文提出的方法計算的應力-應變結(jié)果與線圈實際的結(jié)果誤差控制在5%以內(nèi).在滿足精確性需求的同時,多尺度分析方法是在均質(zhì)化模型的基礎上,根據(jù)位移荷載計算超導線單元內(nèi)各材料的力學行為,簡化了復合線圈模型的復雜建模過程同時不失準確性,因此本文提出的多尺度分析方法計算精度高且計算代價低.依據(jù)此方法計算超導線圈運行過程中電磁力作用下的應力-應變結(jié)果并得到如下結(jié)論,超導線圈內(nèi)側(cè)的應力高于線圈其他區(qū)域,即內(nèi)側(cè)容易發(fā)生強度失效破壞.組成線圈的這三種材料中環(huán)氧樹脂的最大主應力數(shù)值最低,Nb3Sn 芯絲的最大主應力數(shù)值最大.最大主應力數(shù)值隨著層數(shù)的增加逐漸減小,隨著匝數(shù)的變化呈對稱分布.從超導線圈不同位置的徑向和軸向應變曲線可知,線圈內(nèi)側(cè)中間處的軸向應變最大,線圈中間層的徑向應變較大.根據(jù)這些結(jié)果可以準確預測超導線圈在電磁體力作用下的危險位置和力學失效行為,為超導磁體的安全穩(wěn)定運行提供理論依據(jù).