考慮材料各向異性的熔絲制造PLA 點(diǎn)陣結(jié)構(gòu)彈性各向同性設(shè)計(jì)1)
王書恒 戴 時(shí) 吳鑫偉 馬永彬 鄧子辰
(西北工業(yè)大學(xué)工程力學(xué)系,西安 710129)
(復(fù)雜系統(tǒng)動(dòng)力學(xué)與控制工業(yè)和信息化部重點(diǎn)實(shí)驗(yàn)室,西安 710072)
引言
諸多國(guó)家重大工業(yè)裝備及其極端服役環(huán)境均對(duì)高性能、輕量化的結(jié)構(gòu)提出了迫切需求.材料-結(jié)構(gòu)一體化設(shè)計(jì)是獲得高性能、輕量化結(jié)構(gòu)最有效的途徑之一.以增材制造技術(shù)為代表的先進(jìn)制造技術(shù)的快速發(fā)展,極大地拓展了裝備結(jié)構(gòu)的選材和創(chuàng)新設(shè)計(jì)空間[1-4],為實(shí)現(xiàn)材料-結(jié)構(gòu)一體化設(shè)計(jì)提供了最有力的保障.輕質(zhì)點(diǎn)陣結(jié)構(gòu)因具有極大的可設(shè)計(jì)空間和多功能特性已廣泛應(yīng)用于航空航天、船舶汽車等工程領(lǐng)域[5-7].然而,目前多數(shù)點(diǎn)陣結(jié)構(gòu)的力學(xué)性能呈現(xiàn)明顯的各向異性,它們僅在部分方向上具有較高的承載能力[8].結(jié)構(gòu)的各向異性在許多應(yīng)用中被視為一種有害的特性,特別是當(dāng)各向異性結(jié)構(gòu)被用作結(jié)構(gòu)構(gòu)件或者能量吸收材料時(shí),由于工程中的載荷往往存在不確定性,在這種情況下自然不希望結(jié)構(gòu)部件在部分方向上的力學(xué)性能明顯較弱[9-10].此外,由于增材制造技術(shù)大多遵循“點(diǎn)-線-面-體”的“增材”制造過(guò)程,材料在制備成形過(guò)程中往往會(huì)發(fā)生多種相變,使得最終材料內(nèi)部存在許多孔洞和裂紋等缺陷,力學(xué)性能上也呈現(xiàn)不同程度的各向異性[4,11-17],從而增加了增材制造材料與結(jié)構(gòu)力學(xué)性能預(yù)測(cè)與設(shè)計(jì)的難度.
熔絲制造技術(shù),也稱為熔融沉積成型技術(shù),以成本低、操作方便以及原材料種類多而廣泛使用.國(guó)內(nèi)外學(xué)者圍繞熔絲制造材料力學(xué)性能各向異性開展了廣泛研究工作.Zou 等[18]采用各向同性和橫觀各向同性模型來(lái)預(yù)測(cè)不同打印角度下ABS 材料的力學(xué)性能,發(fā)現(xiàn)橫觀各向同性模型預(yù)測(cè)得到的結(jié)果更為準(zhǔn)確.Xia 等[19]和徐可[20]基于橫觀各向同性假設(shè)建立了ABS 材料的彈塑性本構(gòu)模型并通過(guò)實(shí)驗(yàn)測(cè)試和數(shù)值仿真驗(yàn)證了模型的準(zhǔn)確性.另有研究表明,對(duì)于熔絲制造材料,采用正交各向異性模型比橫觀各向同性模型更為合適[21-23].Casavola 等[21]強(qiáng)調(diào)了熔絲制造PLA 材料和ABS 材料的正交各向異性力學(xué)行為,并采用經(jīng)典層合板理論預(yù)測(cè)他們的力學(xué)行為.Dai 等[22]將熔絲制造PLA 材料視為正交各向異性復(fù)合材料,并推導(dǎo)出了任意方向上材料彈性模量和屈服強(qiáng)度的理論預(yù)測(cè)公式.Biswas 等[23]基于熔絲制造PLA 材料的微觀CT 模型,結(jié)合數(shù)值均勻化方法得到了材料正交各向異性彈性本構(gòu)矩陣,并指出材料的孔隙率越大,其各向異性程度越明顯.此外,由于熔絲制造的工藝參數(shù)對(duì)其打印材料的性能有較大的影響[16],通過(guò)調(diào)整工藝參數(shù)能夠有效調(diào)整成形材料的各向異性[24].
目前,已有大量工作圍繞點(diǎn)陣結(jié)構(gòu)的各向同性設(shè)計(jì)或各向異性控制展開[8-10,25-32].在工程中使用各向同性點(diǎn)陣結(jié)構(gòu),不僅可以不用考慮載荷可能出現(xiàn)的方向,還可以避免裝配偏差帶來(lái)的影響.目前,獲得各向同性點(diǎn)陣結(jié)構(gòu)或者調(diào)整點(diǎn)陣結(jié)構(gòu)各向異性程度的方法大致可分為兩類.一類是基于算法通過(guò)形狀或者拓?fù)鋬?yōu)化來(lái)獲得彈性各向同性點(diǎn)陣結(jié)構(gòu)[25-27].另一類主要是基于研究者的經(jīng)驗(yàn),在固定的單胞結(jié)構(gòu)構(gòu)型下,通過(guò)使用均勻化方法[9,33-35]調(diào)整點(diǎn)陣結(jié)構(gòu)的幾何參數(shù)和材料的性能參數(shù)來(lái)實(shí)現(xiàn)結(jié)構(gòu)彈性性能的各向同性設(shè)計(jì)或者是各向異性控制.主要設(shè)計(jì)方法包括將兩個(gè)或者多個(gè)各向異性互補(bǔ)的單胞結(jié)構(gòu)進(jìn)行組合[8-10,28],采用變直徑桿[29]或者空心桿[30]代替桁架結(jié)構(gòu)中的直桿,或者在單胞結(jié)構(gòu)的不同部位使用不同性能的材料[31-32]等.然而,上述研究中大多假設(shè)點(diǎn)陣結(jié)構(gòu)的母體材料是理想各向同性的,很少考慮到實(shí)際成形材料的各向異性,從而導(dǎo)致理論預(yù)測(cè)與設(shè)計(jì)結(jié)果與實(shí)驗(yàn)結(jié)果之間存在較大的差距.因此,在實(shí)際工程中使用增材制造材料或點(diǎn)陣結(jié)構(gòu)時(shí),需要充分考慮材料的各向異性帶來(lái)的一系列影響.
本文基于正交各向異性彈性假設(shè),結(jié)合實(shí)驗(yàn)建立了熔絲制造PLA 材料的彈性模型,推導(dǎo)出了成形后PLA 材料任意方向上彈性模量的理論預(yù)測(cè)公式.設(shè)計(jì)了一種力學(xué)性能可調(diào)的二維組合桁架點(diǎn)陣結(jié)構(gòu),考慮材料的各向異性,基于代表體元法,推導(dǎo)出了點(diǎn)陣結(jié)構(gòu)的彈性性能的解析表達(dá)式和彈性各向同性條件,結(jié)合實(shí)驗(yàn)驗(yàn)證了預(yù)測(cè)結(jié)果的準(zhǔn)確性和設(shè)計(jì)的有效性,以期為熔絲制造材料和點(diǎn)陣結(jié)構(gòu)力學(xué)性能的預(yù)測(cè)與設(shè)計(jì)提供參考.
1 材料與實(shí)驗(yàn)
1.1 3D 打印機(jī)器、材料與微觀結(jié)構(gòu)
本文使用Raise3D Pro2 桌面級(jí)3D 打印機(jī)來(lái)制備所有實(shí)驗(yàn)所需的試件,Raise3D Pro2 配備電動(dòng)雙噴嘴擠出系統(tǒng),可以同時(shí)打印兩種不同的材料,為了使打印出的點(diǎn)陣結(jié)構(gòu)效果更好,選取 0.2 mm 直徑的噴嘴,并且在打印過(guò)程中使用單一噴嘴模式.
選取上海Ploymaker 公司生產(chǎn)的Polylite PLA材料(直徑1.75 mm)作為打印材料.在打印過(guò)程中,PLA 細(xì)絲在噴嘴中熔融,隨著噴嘴在設(shè)置好的路線上以熔絲的形式擠出并凝固成型,由點(diǎn)到線、由線到面,逐層累加形成實(shí)體.打印試件的模型在SolidWorks 2014?中創(chuàng)建,并以stl 格式輸出到切片軟件中設(shè)置打印參數(shù),由于工藝參數(shù)對(duì)打印材料力學(xué)性能影響較大,整個(gè)打印過(guò)程中需要保持工藝參數(shù)恒定,具體的工藝參數(shù)設(shè)置列于表1.

表1 熔絲制造工藝參數(shù)Table 1 Process parameters of fused filament fabrication
圖1 是熔絲制造成形后PLA 材料的掃描電鏡(SEM) 結(jié)果,可以清楚觀測(cè)到成形后PLA 材料的微觀結(jié)構(gòu).如圖1 所示,成形熔絲呈現(xiàn)橢圓狀,這是重力作用和下一層打印時(shí)噴嘴的擠壓導(dǎo)致.熔絲之間存在明顯的氣隙,氣隙的分布在不同方向上差距明顯.因此,成形后PLA 材料的三維微觀結(jié)構(gòu)模型可以簡(jiǎn)化為圖2,并在圖1 和圖2 中定義了三個(gè)材料方向,包括熔絲方向、層內(nèi)方向和重力方向,圖1 中的熔絲方向垂直于圖片.由圖1 和圖2 可以看出,這三個(gè)方向相互垂直,且PLA 材料的微觀結(jié)構(gòu)在這三個(gè)方向上具有明顯的差異,因此材料在這三個(gè)方向上的力學(xué)性能可能會(huì)有一定的差異.

圖1 熔絲制造PLA 材料微觀結(jié)構(gòu)Fig.1 Microstructure of PLA material in fused filament fabrication
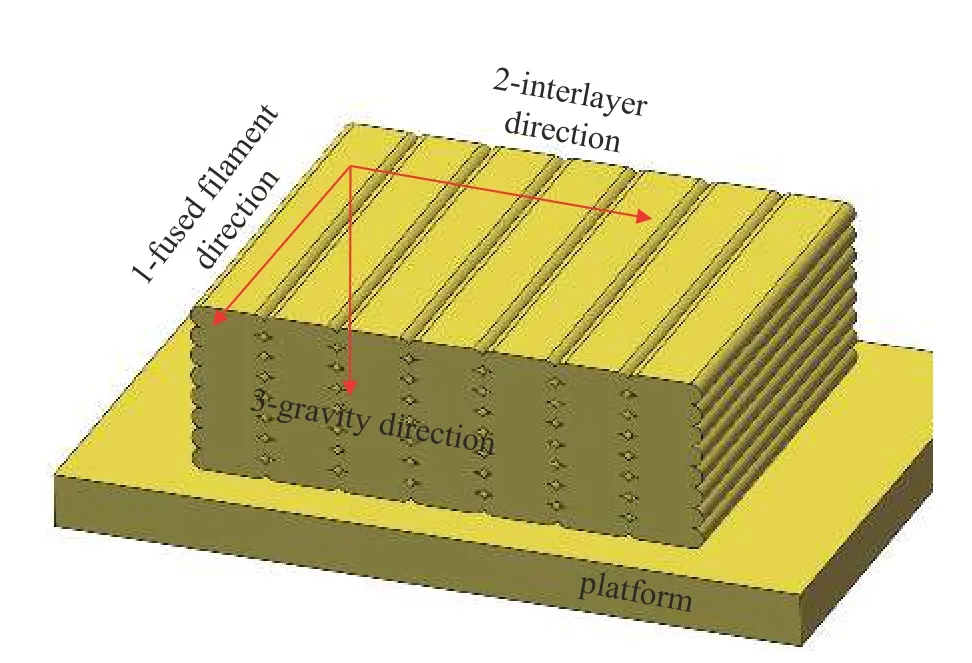
圖2 熔絲制造PLA 材料微觀結(jié)構(gòu)簡(jiǎn)化模型Fig.2 Simplified model of microstructure of PLA material in fused filament fabrication
1.2 拉伸試件尺寸與方向
為了通過(guò)實(shí)驗(yàn)獲得成形后PLA 材料的力學(xué)性能,參考ISO 527-2-2012 (國(guó)際標(biāo)準(zhǔn),塑料拉伸性能的測(cè)定,第二部分:模塑和擠塑塑料的試驗(yàn)條件),設(shè)計(jì)了單軸拉伸試件,試件的幾何尺寸如圖3 所示.根據(jù)PLA 材料的微觀結(jié)構(gòu),可以采用正交各向異性彈性模型來(lái)描述材料的彈性行為,因此需要通過(guò)實(shí)驗(yàn)測(cè)得材料九個(gè)獨(dú)立的彈性常數(shù),它們分別是E1,E2,E3,v12,v13,v23,G12,G13和G23.為了通過(guò)單軸拉伸實(shí)驗(yàn)測(cè)得這九個(gè)獨(dú)立的彈性常數(shù),設(shè)計(jì)了如圖4 所示的九個(gè)不同方向上的試件,它們分別位于A,B和C三個(gè)平面內(nèi).同時(shí),在圖4 中定義了兩個(gè)三維直角坐標(biāo)系,它們是全局坐標(biāo)系(1 -2-3)和局部坐標(biāo)系(x-y-z).
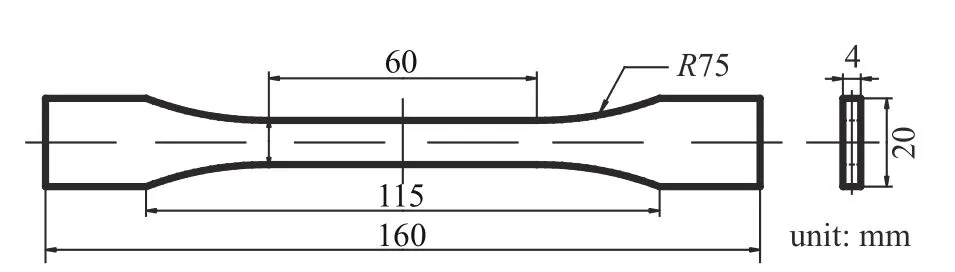
圖3 基于ISO 527-2-2012 的拉伸試件的尺寸Fig.3 Dimensions of tensile specimen based on ISO 527-2-2012
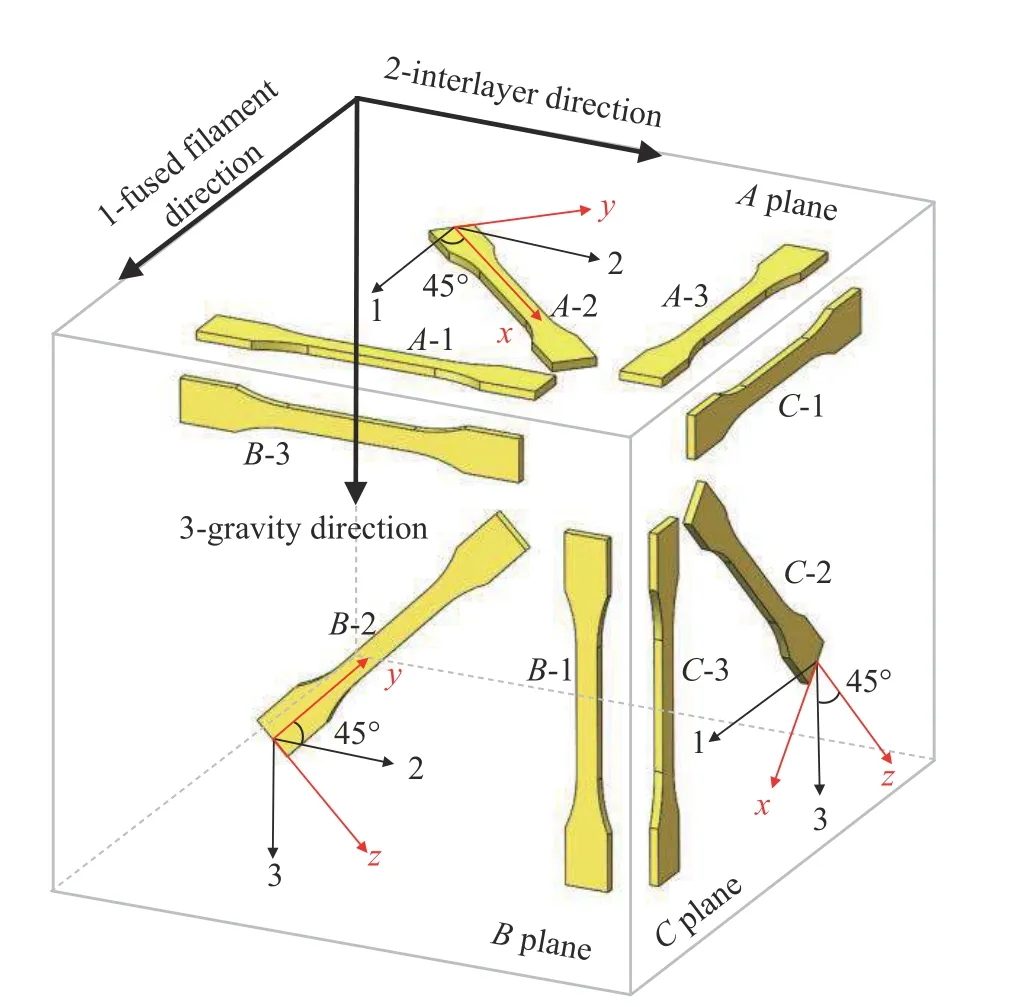
圖4 不同方向上打印的拉伸試件、全局坐標(biāo)系和局部坐標(biāo)系示意圖Fig.4 Schematic diagram of tensile specimens printed in different directions,global,and local coordinate systems
1.3 彈性常數(shù)
PLA 材料的彈性模量和泊松比可以直接通過(guò)單軸拉伸實(shí)驗(yàn)測(cè)得,單軸拉伸實(shí)驗(yàn)在島津電子萬(wàn)能試驗(yàn)機(jī)(AGS-X)上進(jìn)行,拉伸的速度設(shè)為1 mm/min.在本文中,針對(duì)不同的彈性常數(shù),采用兩種方式來(lái)獲取應(yīng)變.一是采用引伸計(jì)記錄單軸拉伸過(guò)程中標(biāo)定段的位移,如圖5(a) 所示,這種方式可以獲得試件在拉伸方向上的彈性模量.二是采用應(yīng)變片 (35 BHI120-3 BB-E-L30) 記錄單軸拉伸過(guò)程中試件在拉伸方向及其垂直方向上的應(yīng)變,如圖5(b) 所示,這種方式可以獲得試件的泊松比.對(duì)于圖4 中不同方向的試件,通過(guò)單軸拉伸實(shí)驗(yàn)可以獲得對(duì)應(yīng)的彈性常數(shù),對(duì)應(yīng)關(guān)系列于表2 中.此外,若假設(shè)成形后PLA材料是正交各向異性的,其彈性模量與泊松比需要滿足以下約束條件
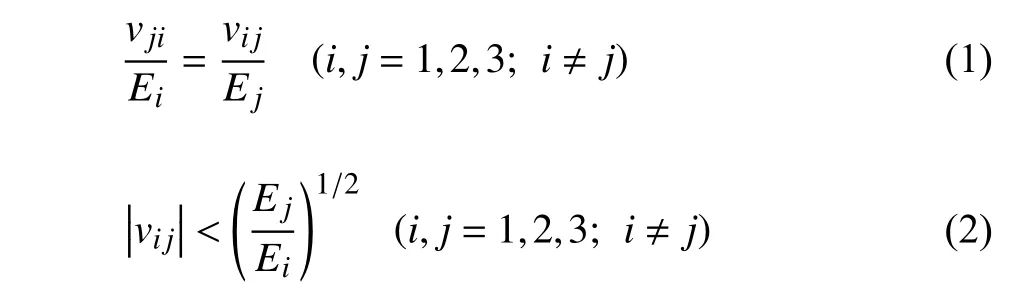
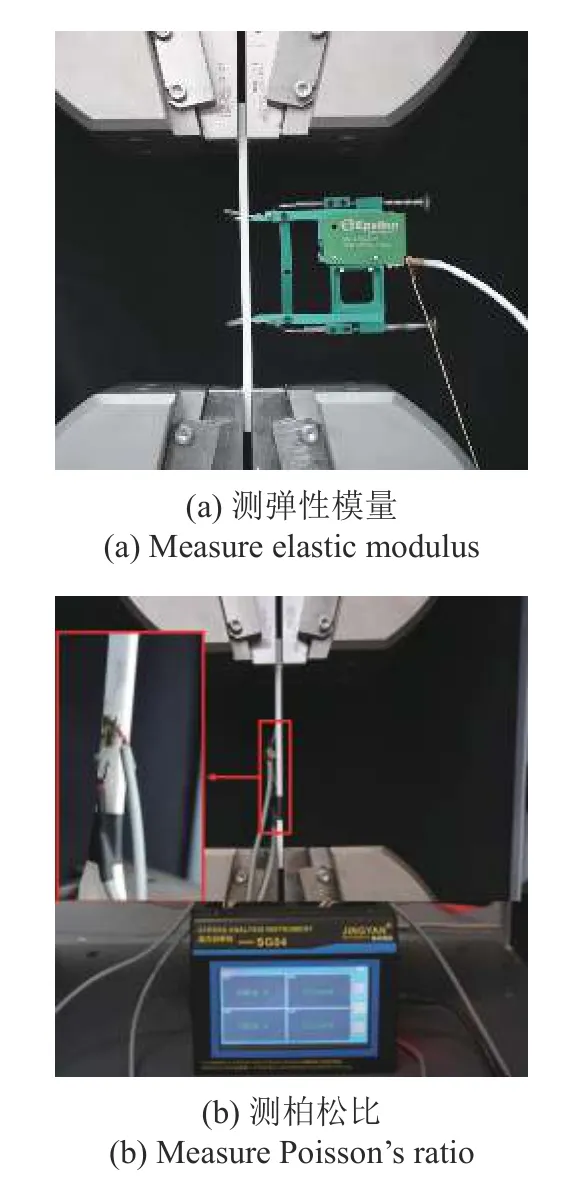
圖5 單軸拉伸實(shí)驗(yàn)設(shè)置Fig.5 Setup of uniaxial tensile test
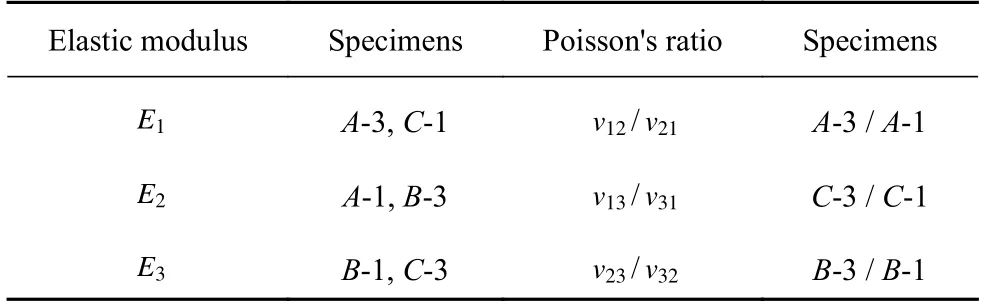
表2 試件與彈性常數(shù)對(duì)應(yīng)關(guān)系Table 2 Correspondence between specimen and elastic constants
式中,v為泊松比,E為彈性模量.
材料的剪切模量難以通過(guò)拉伸標(biāo)準(zhǔn)試件直接獲得,對(duì)于正交各向異性材料,彈性常數(shù)間的關(guān)系較為復(fù)雜,公式Gij=Ei/[2(1+vij)](i,j=1,2,3;i≠j) 已不再適用.由試件的尺寸可知,在單軸拉伸下,試件處于平面應(yīng)力狀態(tài).因此,正交各向異性材料的剪切模量可以由以下公式[24]得到
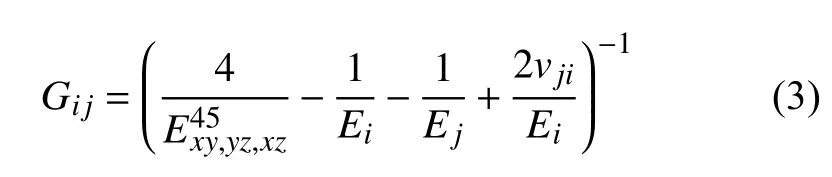
除了如圖4 所示的九個(gè)不同方向上的試件之外,還額外設(shè)計(jì)了其他三組不同打印方向的試件并進(jìn)行制備和單軸拉伸測(cè)試,以驗(yàn)證理論模型的準(zhǔn)確性,為了保證實(shí)驗(yàn)結(jié)果的可靠性,每組試件制備了五個(gè),如圖3 所示的拉伸試件一共制備了60 個(gè).
2 彈性力學(xué)模型與理論預(yù)測(cè)公式
2.1 正交各向異性彈性模型
由上節(jié)的分析可知,成形后PLA 材料在熔絲方向,層內(nèi)方向和重力方向上的力學(xué)性能有一定的差異,且這三個(gè)方向互相垂直.因此,本節(jié)建立了熔絲制造PLA 材料的正交各向異性彈性模型.
對(duì)于正交各向異性材料,其彈性性能的本構(gòu)關(guān)系如下

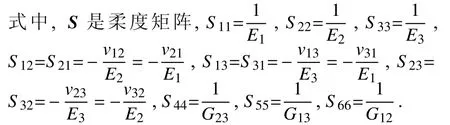
由于3D 打印技術(shù)的靈活性,設(shè)計(jì)好的模型輸出到切片軟件后可以旋轉(zhuǎn)到任意的位置進(jìn)行打印,并能夠?qū)υ嚰M(jìn)行平移、縮放、旋轉(zhuǎn)等操作,因此,通過(guò)全局坐標(biāo)系下測(cè)得的材料的本構(gòu)模型去計(jì)算任意局部坐標(biāo)系下材料的力學(xué)性能具有重要意義.本節(jié)采用Bond 變換矩陣[36],首先,將全局坐標(biāo)系(1 -2-3) 下測(cè)得的材料的柔度矩陣轉(zhuǎn)換到局部坐標(biāo)系 (x-y-z),然后將柔度矩陣求逆得到局部坐標(biāo)系下材料的剛度矩陣,最后基于局部坐標(biāo)系下材料的剛度矩陣,得到材料在任意方向上彈性模量的預(yù)測(cè)公式.
圖6 展示了由全局坐標(biāo)系 (1 -2-3) 轉(zhuǎn)換到局部坐標(biāo)系 (x-y-z) 的過(guò)程,首先,全局坐標(biāo)系 (1-2-3) 繞著3 軸旋轉(zhuǎn)角度φ ,變?yōu)閤′-y′-z′坐標(biāo)系.然后,x′-y′-z′坐標(biāo)系再繞著y′軸旋轉(zhuǎn)角度 θ,變?yōu)榫植孔鴺?biāo)系x-y-z.由全局坐標(biāo)系轉(zhuǎn)換到局部坐標(biāo)系的方式有很多,本節(jié)介紹的只是其中一種.全局坐標(biāo)系(1 -2-3 ) 與局部坐標(biāo)系 (x-y-z) 之間的轉(zhuǎn)換關(guān)系可由坐標(biāo)之間的方向余弦來(lái)表示,按照如圖6 所示的轉(zhuǎn)換順序得到的方向余弦矩陣為
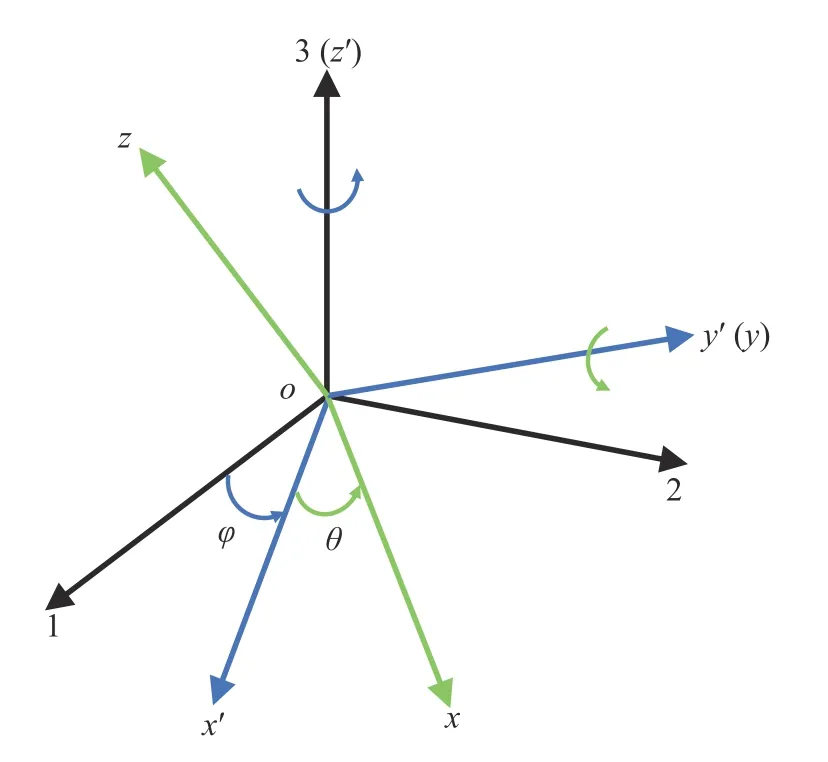
圖6 全局坐標(biāo)系轉(zhuǎn)換到局部坐標(biāo)系示意圖Fig.6 Diagram of transformation from global to local coordinate system
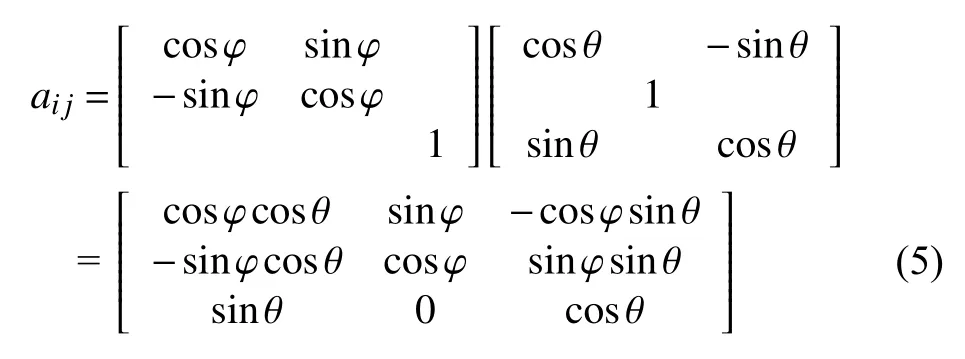
式中,aij(i,j=1,2,3) 是方向余弦.
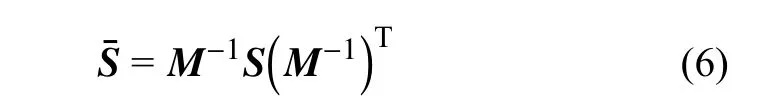
式中矩陣M是Bond應(yīng)力變換矩陣[36],M-1是矩陣M的逆,表示矩陣M-1的轉(zhuǎn)置,矩陣M可以用方向余弦表示為
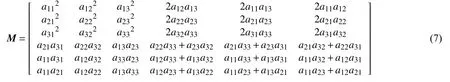
通過(guò)式(5)~式(7) 可以獲得材料在任意局部坐標(biāo)系下的柔度矩陣,結(jié)合式(4) 可以求得材料在任意方向上的彈性性能.
2.2 實(shí)驗(yàn)結(jié)果與彈性模量預(yù)測(cè)公式
通過(guò)單軸拉伸實(shí)驗(yàn)測(cè)得的材料彈性常數(shù)和基于式(3) 計(jì)算得到的剪切模量的平均值如表3 所示,可以看出,成形后PLA 材料在熔絲方向、層內(nèi)方向以及重力方向上的彈性模量均有一定的差異,熔絲方向上PLA 材料的彈性模量最大,重力方向上次之,層內(nèi)方向最小.這是由于在熔絲方向上,材料的變形主要取決于噴嘴擠出的PLA 熔絲的變形,而材料層內(nèi)方向和重力方向上的變形能力不僅依賴于PLA熔絲的變形,還更多地依賴于PLA 熔絲之間的粘結(jié).成形后PLA 材料層內(nèi)方向的彈性模量小于重力方向上的彈性模量的主要原因有兩種,一是在打印過(guò)程中噴嘴是沿著重力方向逐層向上打印的,每一層成形后都會(huì)在下一層打印時(shí)受到噴嘴的擠壓,這樣會(huì)使得層間或者是重力方向上PLA 熔絲之間的接觸面積增大,結(jié)合更加緊密,粘合增強(qiáng);二是由于重力作用,導(dǎo)致層間或者是重力方向上PLA 熔絲之間的接觸面積增大,粘合增強(qiáng),這也可以從圖1 所示的PLA 材料微觀結(jié)構(gòu)掃描電鏡圖看出.
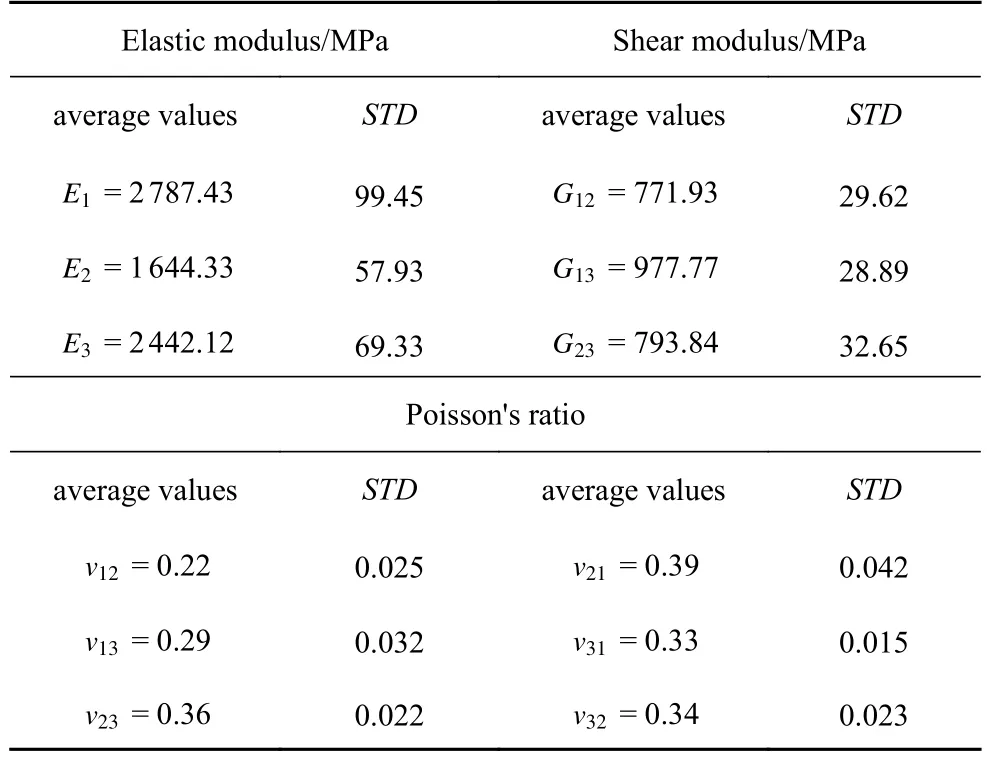
表3 彈性常數(shù)測(cè)試結(jié)果(彈性模量,泊松比)與計(jì)算結(jié)果(剪切模量)的平均值Table 3 Average values of measureed (elastic modulus,Poisson’s ratio) and calculated (shear modulus) results of elastic constants
經(jīng)過(guò)計(jì)算驗(yàn)證發(fā)現(xiàn),表3 中的彈性常數(shù)的值滿足式(1)和式(2),具有一定的可靠性.將彈性常數(shù)代入到式(4) 中,可以獲得材料在全局坐標(biāo)系下的柔度矩陣,并將其與式(5)~式(8)結(jié)合,可以得到PLA 材料在任意局部坐標(biāo)系下的柔度矩陣.同時(shí),也能夠得到PLA 材料在任意方向上的彈性常數(shù)值,例如以熔絲方向?yàn)槌跏挤较?PLA 材料任意方向上彈性模量的預(yù)測(cè)公式可以表示如下

式中,參數(shù)A,B,C,D,E,F,G,H和I是常數(shù),其數(shù)值列在表4 中.
根據(jù)式(8) 也可以得到材料任意平面內(nèi)彈性模量的預(yù)測(cè)公式,例如,在A,B和C三個(gè)平面內(nèi)材料彈性模量的預(yù)測(cè)公式分別為
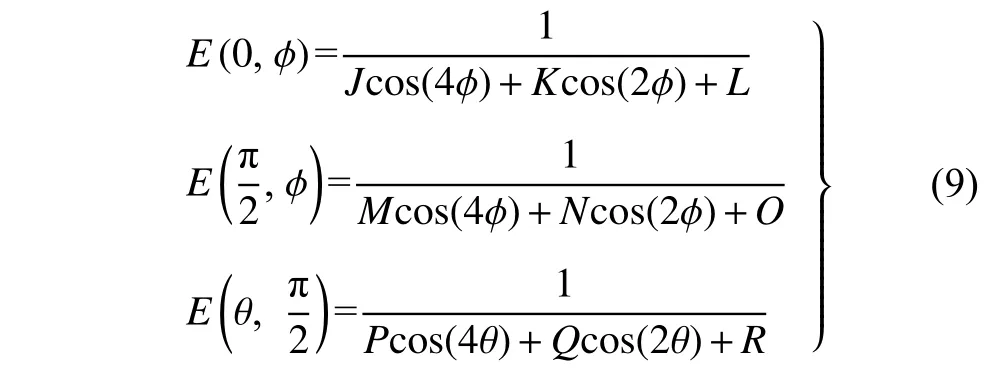
式中,參數(shù)J,K,L,M,N,O,P,Q和R是常數(shù),其數(shù)值列在表4 中.
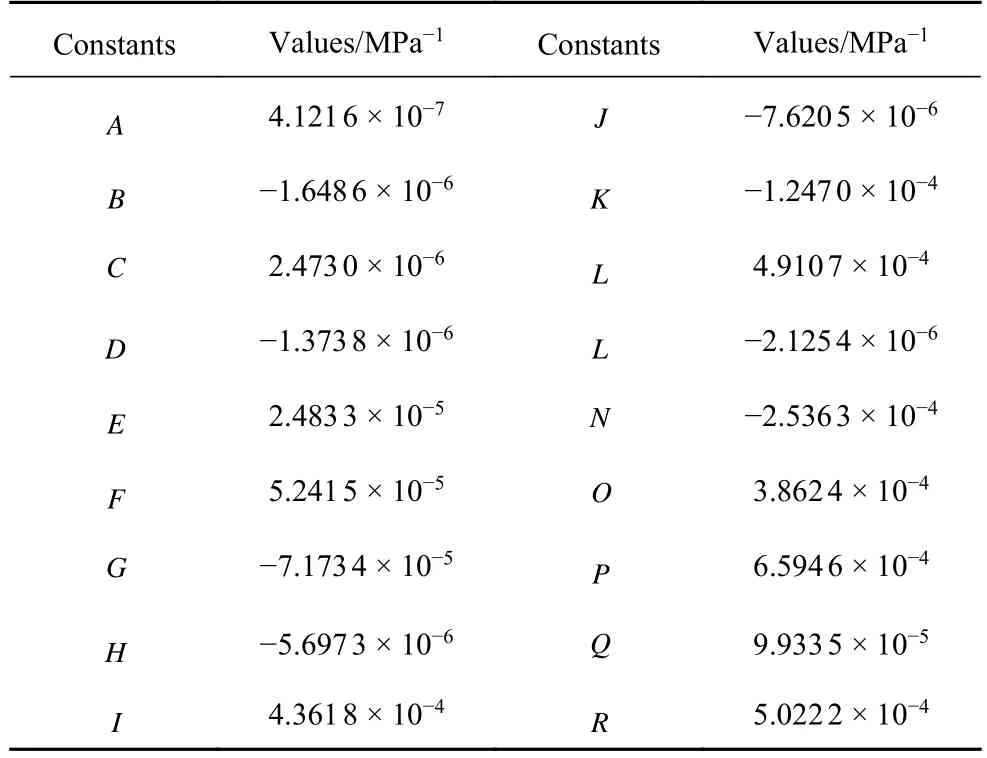
表4 公式 (8) 和 (9) 中的參數(shù)值Table 4 Values of the constants in Eqs.(9) and (10)
根據(jù)式(8)和式(9)可以分別繪制出熔絲制造PLA 材料彈性模量在空間內(nèi)的曲面圖以及A,B和C平面內(nèi)的曲線圖,如圖7 所示,可以清晰地看出PLA 材料彈性模量的各向異性程度及其在不同方向上的大小,當(dāng)實(shí)際應(yīng)用中的載荷方向已知時(shí),能夠?yàn)樽畲蠡睦貌牧系男阅芴峁┮欢ǖ膮⒖?
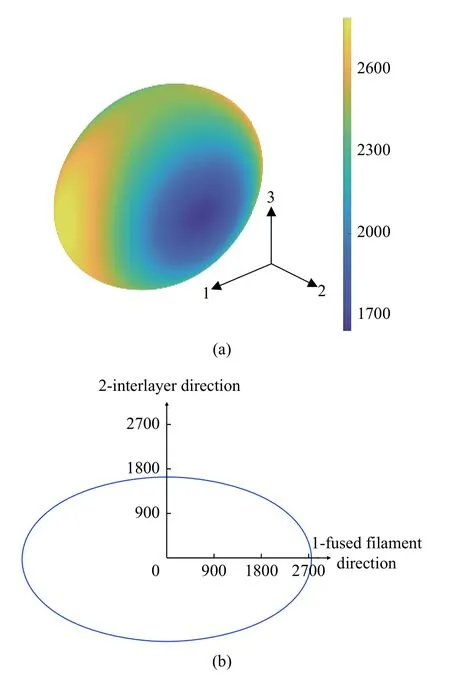
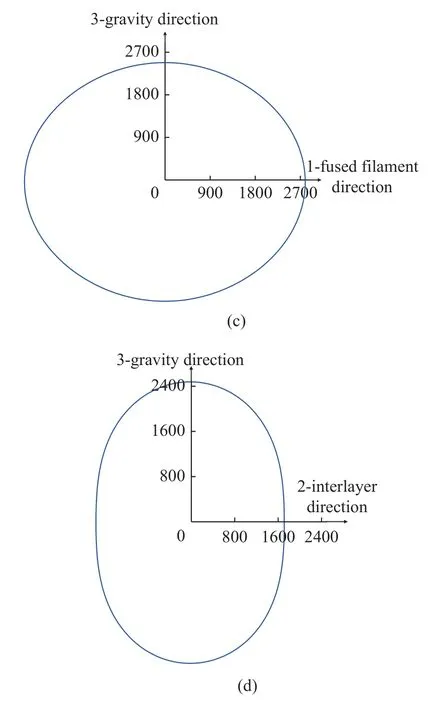
圖7 (a) PLA 材料彈性模量在空間內(nèi)的曲面圖;(b)-(d) PLA 材料彈性模量分別在A,B 和C 平面內(nèi)的曲線圖Fig.7 (a) Surface diagram of elastic modulus of PLA material in space.(b)-(d) Curves of elastic modulus of PLA material in A,B and C planes,respectively
為了驗(yàn)證PLA 材料正交各向異性彈性模型以及彈性模量預(yù)測(cè)公式的準(zhǔn)確性,在制備和拉伸如圖4所示九個(gè)不同方向的標(biāo)準(zhǔn)試件的同時(shí),也制備和測(cè)試了三組其他不同方向的試件,它們的測(cè)試方向以及測(cè)試結(jié)果平均值與實(shí)驗(yàn)結(jié)果的對(duì)比在表5 中列出.經(jīng)過(guò)對(duì)比,可以發(fā)現(xiàn)實(shí)驗(yàn)測(cè)得的結(jié)果與理論預(yù)測(cè)的結(jié)果吻合良好,誤差均小于8%,從一定程度上驗(yàn)證了模型的準(zhǔn)確性.
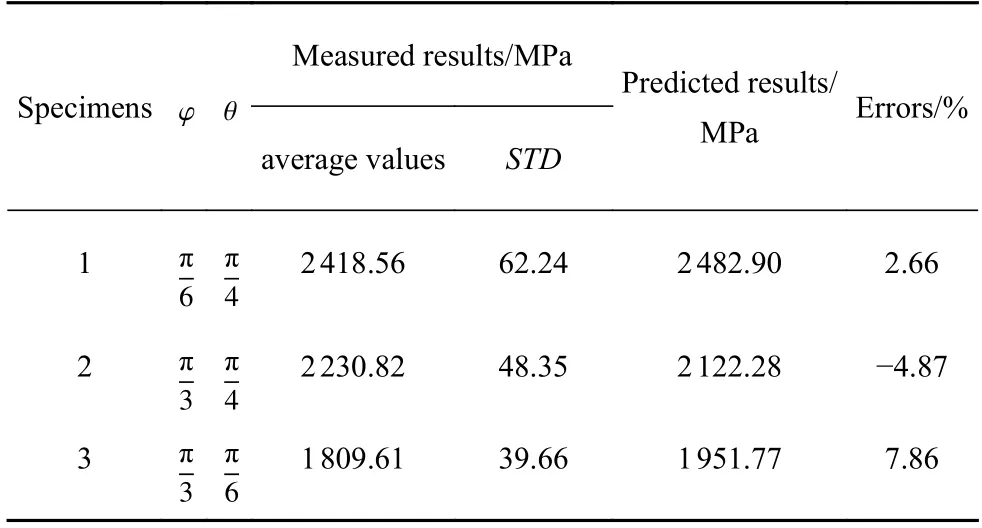
表5 不同方向上PLA 材料彈性模量測(cè)試結(jié)果平均值與預(yù)測(cè)結(jié)果對(duì)比Table 5 Comparison of average measured and predicted results of elastic modulus of PLA material in different directions
3 彈性各向同性組合桁架點(diǎn)陣結(jié)構(gòu)設(shè)計(jì)
3.1 組合桁架點(diǎn)陣結(jié)構(gòu)設(shè)計(jì)
眾所周知,正方形結(jié)構(gòu)具有明顯的各向異性,在其邊長(zhǎng)方向上具有很高的剛度和強(qiáng)度,而在其他方向尤其是對(duì)角線方向上的剛度和強(qiáng)度很弱.如圖8所示,將正方形點(diǎn)陣結(jié)構(gòu)先縮放為原來(lái)的,然后旋轉(zhuǎn)45°,獲得的新的正方形點(diǎn)陣結(jié)構(gòu)在原結(jié)構(gòu)的對(duì)角方向上具有較高的剛度和強(qiáng)度,最后再將新舊兩個(gè)正方形點(diǎn)陣結(jié)構(gòu)組合,得到的新的組合點(diǎn)陣結(jié)構(gòu)繼承了原來(lái)兩個(gè)正方形點(diǎn)陣結(jié)構(gòu)的優(yōu)點(diǎn),在水平方向、豎直方向以及對(duì)角方向均具有較高的剛度和強(qiáng)度.組合點(diǎn)陣結(jié)構(gòu)單胞的尺寸也如圖8 所示,結(jié)構(gòu)的面外厚度為b.由之前的研究可知,通過(guò)調(diào)整該組合點(diǎn)陣結(jié)構(gòu)的相對(duì)厚度(t1/t2),能夠有效地調(diào)整結(jié)構(gòu)力學(xué)性能的各向異性[10],實(shí)現(xiàn)該點(diǎn)陣結(jié)構(gòu)的彈性各向同性設(shè)計(jì).

圖8 正方形組合桁架點(diǎn)陣結(jié)構(gòu)設(shè)計(jì)Fig.8 Design of square compound truss lattice structure
3.2 等效彈性性能分析與彈性各向同性設(shè)計(jì)
針對(duì)如圖8 所示的正方形組合桁架點(diǎn)陣結(jié)構(gòu),可以采用代表體元法計(jì)算其等效彈性性能.代表體元法是一種常用于計(jì)算點(diǎn)陣結(jié)構(gòu)等效彈性性能的均勻化方法,其計(jì)算過(guò)程如下:首先需要從點(diǎn)陣結(jié)構(gòu)中選取一個(gè)或者多個(gè)單胞作為代表體元,然后在代表體積元的邊界上施加均勻應(yīng)變或者均勻應(yīng)力邊界條件,最后基于應(yīng)變能等效獲得點(diǎn)陣結(jié)構(gòu)的等效彈性性能[34].根據(jù)作者最近的研究,對(duì)于桁架類點(diǎn)陣結(jié)構(gòu),可以用代表體元法推導(dǎo)出其彈性性能的解析表達(dá)式[35].例如,均勻應(yīng)變邊界條件需要在代表體元的邊界上均勻位移,可以表示為
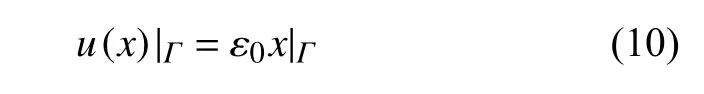
式中 Γ 表示代表體元的邊界,ε0表示指定的應(yīng)變,u表示節(jié)點(diǎn)位移.
根據(jù)應(yīng)變能等效,點(diǎn)陣結(jié)構(gòu)在1 方向上的剛度可以表示為
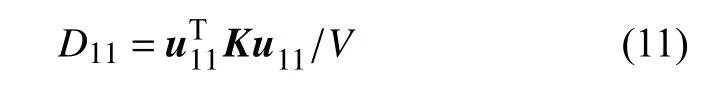
式中,u11表示代表體元在1 方向上的對(duì)應(yīng)于均勻應(yīng)變 ε11的節(jié)點(diǎn)位移向量,K表示代表體元的總體剛度矩陣,V表示代表體元的體積.
對(duì)于如圖8 所示的單胞結(jié)構(gòu),由于其邊界上的節(jié)點(diǎn)數(shù)為2,因此只需要一個(gè)單胞作為代表體元便能得到準(zhǔn)確的計(jì)算結(jié)果[34-35],其節(jié)點(diǎn)編號(hào)如圖9(a) 所示,在1 方向上施加均勻應(yīng)變(ε)邊界條件,其對(duì)應(yīng)的節(jié)點(diǎn)位移向量為
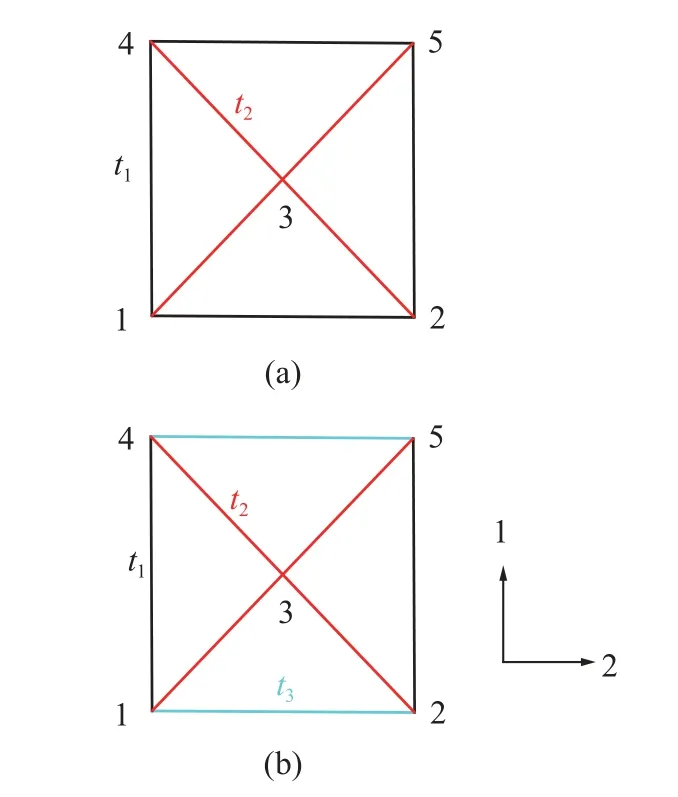
圖9 單胞尺寸及其節(jié)點(diǎn)編號(hào)Fig.9 Size of unit cells and their nodes coding
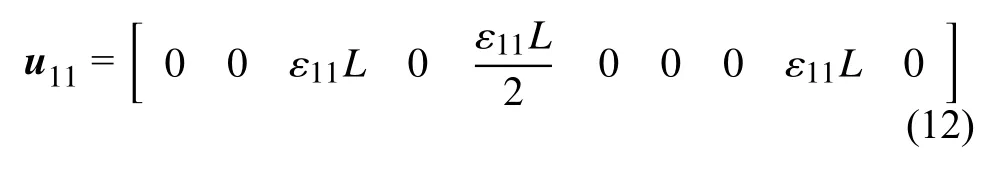
由于組合點(diǎn)陣結(jié)構(gòu)的變形模式屬于拉伸主導(dǎo)型,結(jié)構(gòu)在變形過(guò)程中由桿件的彎曲以及節(jié)點(diǎn)的旋轉(zhuǎn)帶來(lái)的影響可以忽略不計(jì)[39],在代表體元總體剛度矩陣的組裝過(guò)程中可以使用桁架單元.假設(shè)使用的材料是各向同性材料,彈性模量為E,將得到的總體剛度矩陣,節(jié)點(diǎn)位移向量以及代表體元的體積代入式(11) 中,可以得到在1 方向上的等效剛度
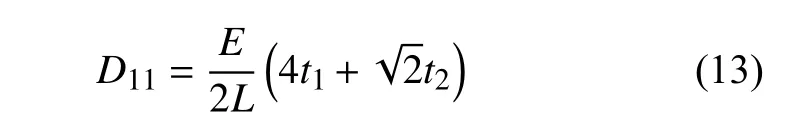
同理可以得到代表體元?jiǎng)偠染仃囍衅渌膮?shù)
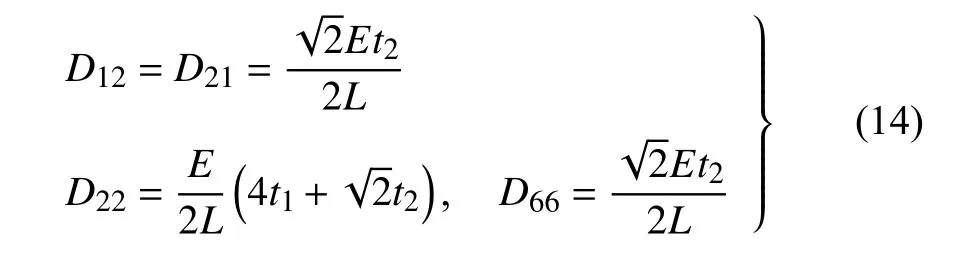
因此,代表體元也就是單胞結(jié)構(gòu)的彈性模量、剪切模量以及泊松比可以用下列方法求解得到
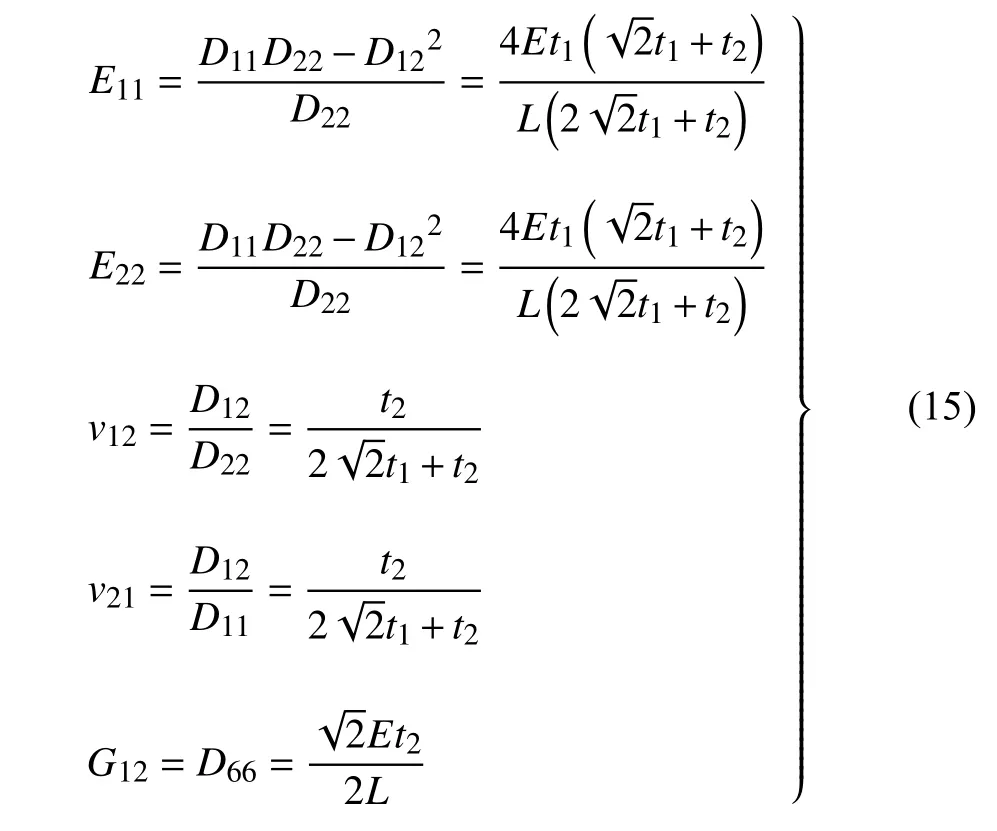
根據(jù)式(15) 可以求得,當(dāng)彈性各向異性參數(shù)[40]ω=2G12(1+v12)/E11=1時(shí),結(jié)構(gòu)的彈性各向同性條件為t2=
對(duì)于二維點(diǎn)陣結(jié)構(gòu),當(dāng)其二維平面與A平面保持平行,且面外方向與重力方向保持一致時(shí),打印的效果最好.因此在實(shí)際制備過(guò)程中按照如圖8 所示的方向來(lái)制備點(diǎn)陣結(jié)構(gòu),1 方向?qū)?yīng)于熔絲方向,2 方向?qū)?yīng)于層內(nèi)方向,A平面內(nèi)材料的彈性模量對(duì)應(yīng)于式(9) 中的E(0,φ) .由圖7(b) 可以清晰地看出,此時(shí)材料在熔絲方向上的彈性模量要大于其在層內(nèi)方向上的彈性模量,圖9(a) 所示的單胞結(jié)構(gòu)在考慮材料的各向異性之后,其在1 方向上的彈性模量必然要大于其在2 方向上的彈性模量,因此可以將單胞結(jié)構(gòu)中水平桿(沿2 方向)的厚度增大以彌補(bǔ)差距,調(diào)整之后的單胞結(jié)構(gòu)如圖9(b) 所示.根據(jù)上述計(jì)算彈性常數(shù)的過(guò)程可以得到圖9(b) 所示單胞結(jié)構(gòu)彈性性能的表達(dá)式,在計(jì)算過(guò)程中只需要調(diào)整結(jié)構(gòu)的總體剛度矩陣,即調(diào)整不同方向上桿件的彈性模量和厚度,節(jié)點(diǎn)位移向量和體積保持不變,計(jì)算結(jié)果如下所示
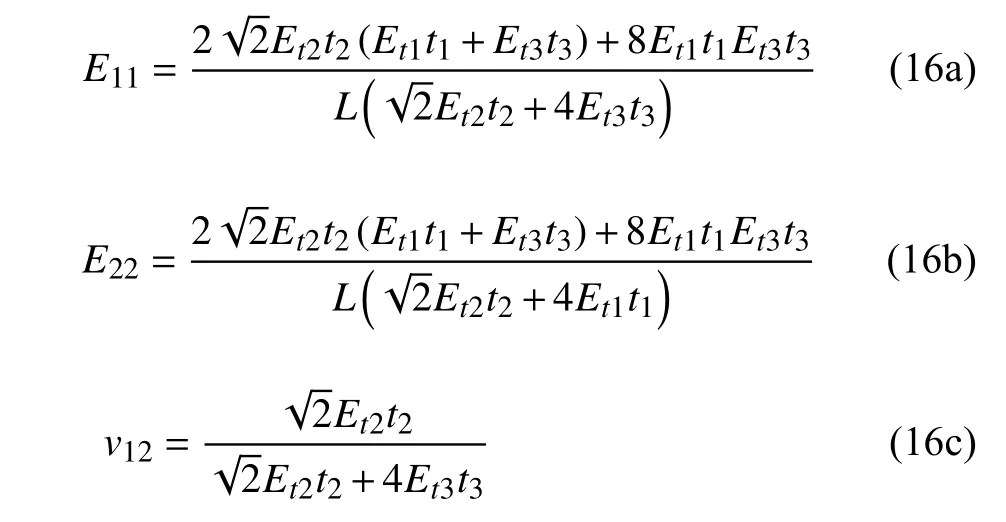

3.3 實(shí)驗(yàn)驗(yàn)證與討論
平面應(yīng)力狀態(tài)下,正交各向異性材料任意方向上的彈性模量可以用以下公式[37]計(jì)算求得
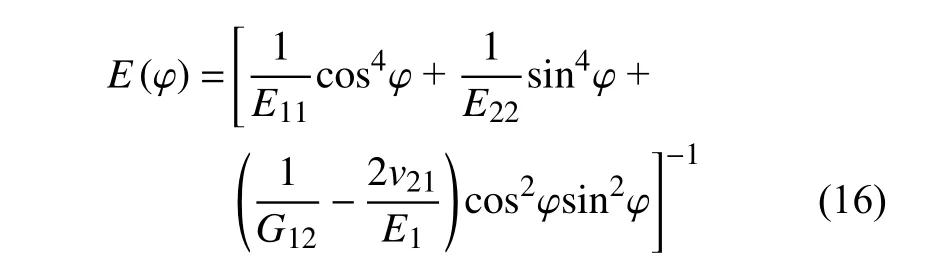
假設(shè)如圖9 (a) 所示的單胞結(jié)構(gòu)的幾何尺寸為t1=1 mm,t2=1.41 mm,L=20 mm,當(dāng)不考慮材料的各向異性時(shí),材料彈性模量取為2 787.43 MPa,將結(jié)構(gòu)的尺寸參數(shù)代入到式(15),并結(jié)合式(17),可以得到單胞結(jié)構(gòu)在面內(nèi)任意方向上彈性模量的極坐標(biāo)圖,如圖10(a) 所示,是各向同性的.當(dāng)考慮材料的各向異性時(shí),將結(jié)構(gòu)的尺寸參數(shù)代入到式(16),令t3=t1,再結(jié)合式(17),得到單胞結(jié)構(gòu)在面內(nèi)任意方向上彈性模量的極坐標(biāo)圖,如圖10(a) 所示,此時(shí)結(jié)構(gòu)不再是彈性各向同性的,而是與PLA 材料在A平面內(nèi)的彈性模量類似(圖7(b)),是正交各向異性的,其在1 方向上的彈性模量大于在2 方向上的彈性模量.假設(shè)圖9(b) 所示的單胞結(jié)構(gòu)的幾何尺寸為t1=0.59 mm,t2=1.16 mm,t3=1 mm,L=20 mm,將這些參數(shù)代入到式(16),并結(jié)合式(17),可以繪制圖9(b) 所示的單胞結(jié)構(gòu)在任意方向上等效彈性模量極坐標(biāo)圖,如圖10(b) 所示,是各向同性的.
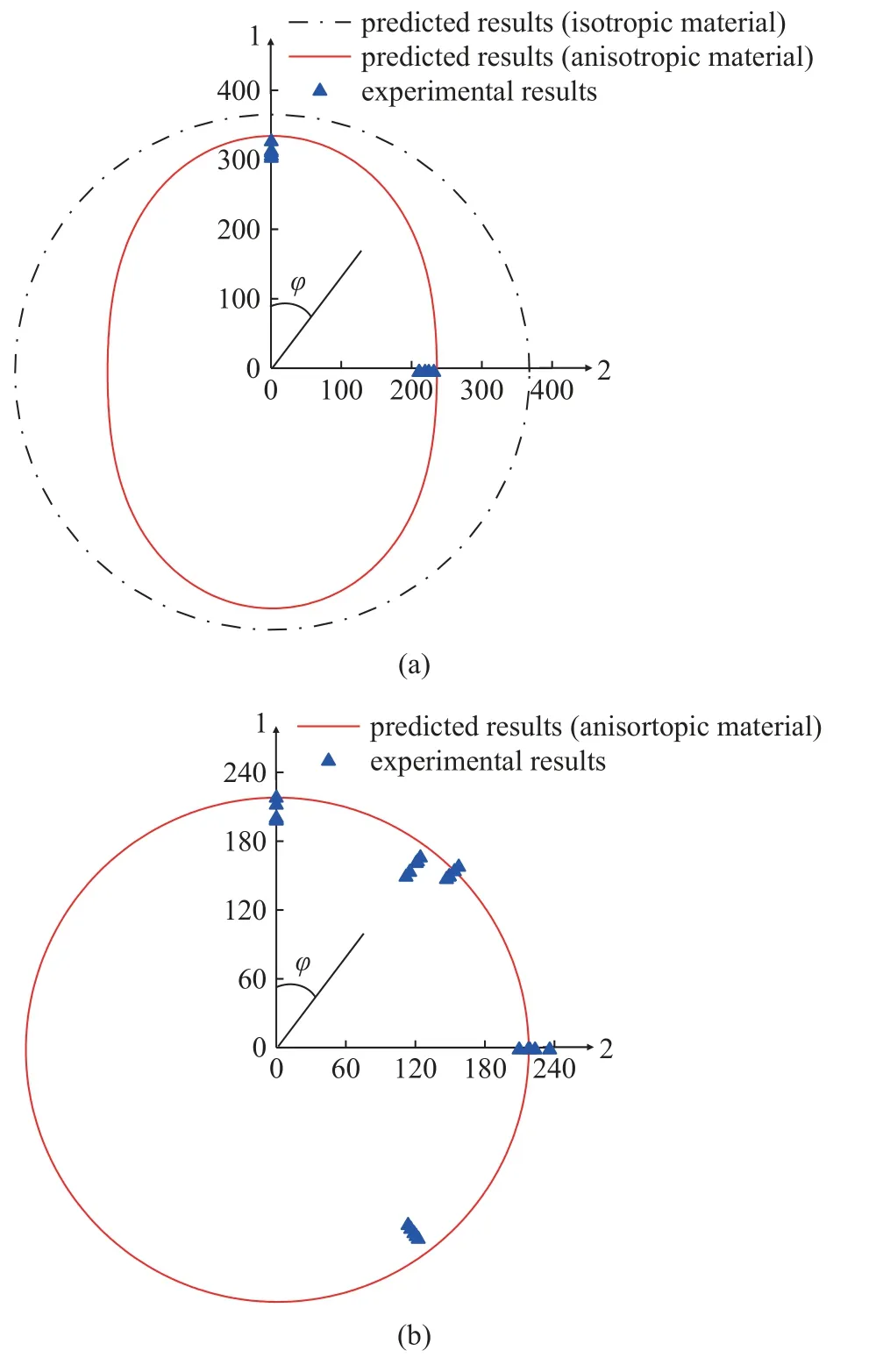
圖10 (a) 如圖9(a) 所示單胞結(jié)構(gòu)在考慮材料各向異性和不考慮材料各向異性情況下平面內(nèi)任意方向上彈性模量的預(yù)測(cè)結(jié)果以及實(shí)驗(yàn)結(jié)果;(b) 如圖9(b) 所示單胞結(jié)構(gòu)在考慮材料各向異性時(shí)平面內(nèi)任意方向上彈性模量的預(yù)測(cè)結(jié)果與實(shí)驗(yàn)結(jié)果Fig.10 (a) Predicted results of elastic modulus in in-plane arbitrary directions with and without considering material anisotropy and experimental results for the unit cell shown in Fig.9(a).(b) Predicted and experimental results of elastic modulus in in-plane arbitrary directions with considering material anisotropy for the unit cell shown in Fig.9(b)
為了驗(yàn)證上述點(diǎn)陣結(jié)構(gòu)彈性模量的計(jì)算結(jié)果的準(zhǔn)確性與各向同性條件的有效性,按照上述假設(shè)的單胞結(jié)構(gòu)的尺寸建立并制備了四種點(diǎn)陣結(jié)構(gòu),點(diǎn)陣結(jié)構(gòu)的測(cè)試方向與幾何尺寸如圖11 和表6 所示,其中,試樣1 的單胞結(jié)構(gòu)如圖9(a) 所示,試樣2~4 其實(shí)是同一種點(diǎn)陣結(jié)構(gòu)的不同選取形式,它們的單胞結(jié)構(gòu)如圖9(b) 所示.試件1 和試件2 可以測(cè)試0°和90°兩個(gè)方向,試件3 可以測(cè)試45°方向,試件4 可以測(cè)試37°和127°兩個(gè)方向,每個(gè)測(cè)試方向的點(diǎn)陣結(jié)構(gòu)制備五個(gè)以保證實(shí)驗(yàn)結(jié)果的可靠性,制備時(shí)采用的工藝參數(shù)與表1 中的參數(shù)保持一致,以減小工藝參數(shù)對(duì)材料力學(xué)性能的影響.采用單軸壓縮實(shí)驗(yàn)來(lái)獲取點(diǎn)陣結(jié)構(gòu)在不同方向上的彈性模量,實(shí)驗(yàn)同樣在島津電子萬(wàn)能試驗(yàn)機(jī)(AGS-X)上進(jìn)行,單軸壓縮的速度設(shè)為1 m m/min,取點(diǎn)陣結(jié)構(gòu)壓縮應(yīng)力應(yīng)變曲線線彈性階段的斜率為彈性模量.

圖11 四種點(diǎn)陣結(jié)構(gòu)試件及其測(cè)試方向Fig.11 Four types of lattice structures and their testing directions
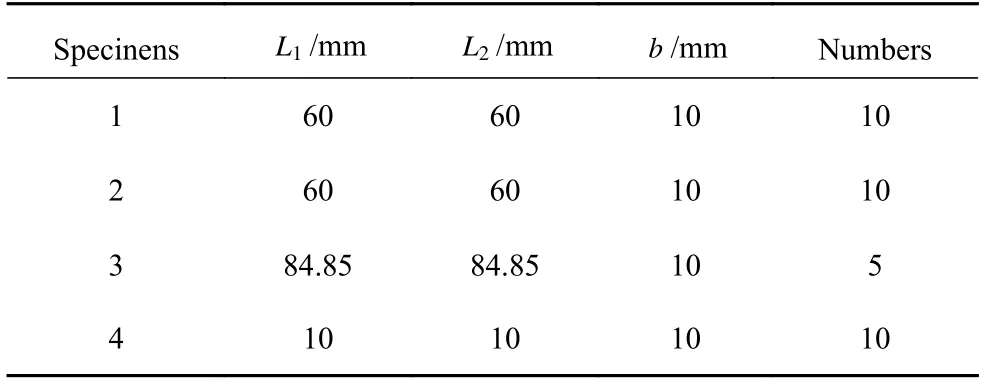
表6 點(diǎn)陣結(jié)構(gòu)的幾何尺寸Table 6 Geometric parameters of the lattice structures
通過(guò)單軸壓縮實(shí)驗(yàn),得到四種點(diǎn)陣結(jié)構(gòu)的彈性模量如圖10 所示,彈性模量測(cè)試結(jié)果的平均值與預(yù)測(cè)結(jié)果的對(duì)比如表7 所示.由圖10 (a) 可以清晰地看出,材料的彈性各向異性對(duì)點(diǎn)陣結(jié)構(gòu)的彈性性能有較大的影響,在不考慮材料各向異性性能時(shí)推導(dǎo)得到的結(jié)構(gòu)的各向同性條件實(shí)際上可能不再適用.由圖10(b) 可以看出,在考慮材料的彈性各向異性之后,重新對(duì)點(diǎn)陣結(jié)構(gòu)進(jìn)行設(shè)計(jì),也能夠理論上獲得使其近似彈性各向同性的條件,從實(shí)驗(yàn)結(jié)果來(lái)看,總體上結(jié)構(gòu)在五個(gè)方向上彈性模量差距不大,且均在理論預(yù)測(cè)結(jié)果附近,彈性模量在90°方向上較45°方向略大,在45°方向上較0°方向略大,在0°方向上較37°和127°方向略大,最大誤差小于12%,主要是由于試件4 相對(duì)不規(guī)則,邊界效應(yīng)對(duì)測(cè)試結(jié)果的影響較大,導(dǎo)致測(cè)試結(jié)果偏小.結(jié)合表7 中的誤差對(duì)比,不難發(fā)現(xiàn)材料的正交各向異性彈性模型適用于預(yù)測(cè)結(jié)構(gòu)的力學(xué)性能,實(shí)驗(yàn)結(jié)果的平均值與預(yù)測(cè)結(jié)果誤差均小于10%,產(chǎn)生誤差的原因可能來(lái)源于設(shè)計(jì)模型與理論模型之間的偏差、打印模型與設(shè)計(jì)模型之間的偏差,以及PLA 材料拉伸性能與壓縮性能存在一定的差異等等.
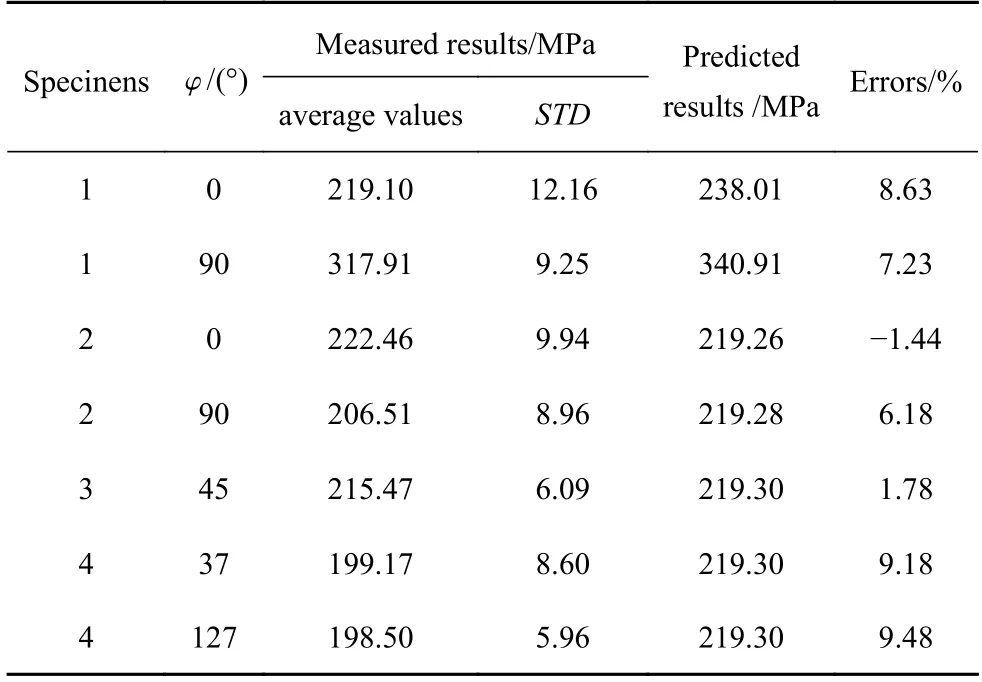
表7 點(diǎn)陣結(jié)構(gòu)彈性模量實(shí)驗(yàn)結(jié)果平均值與預(yù)測(cè)結(jié)果對(duì)比Table 7 Comparison of average measured and predicted results of elastic modulus of the lattice structures
4 結(jié)論
相對(duì)于傳統(tǒng)制造技術(shù),成形材料力學(xué)性能具有各向異性是增材制造技術(shù)的獨(dú)有特點(diǎn),在結(jié)構(gòu)設(shè)計(jì)時(shí)充分考慮材料的各向異性能夠有效地提高設(shè)計(jì)結(jié)果的準(zhǔn)確性.本文針對(duì)熔絲制造技術(shù),采用正交各向異性彈性模型描述成形后PLA 材料的彈性行為,同時(shí)推導(dǎo)出了其任意方向上彈性模量的預(yù)測(cè)公式,設(shè)計(jì)了一種力學(xué)性能可調(diào)的二維組合桁架點(diǎn)陣結(jié)構(gòu),基于代表體元法,推導(dǎo)出了該點(diǎn)陣結(jié)構(gòu)的彈性性能在考慮材料各向異性和不考慮材料各向異性情況下的解析表達(dá)式以及其彈性各向同性條件.
研究結(jié)果表明,熔絲制造PLA 材料具有較強(qiáng)的各向異性,正交各向異性彈性模型能夠較準(zhǔn)確地描述其彈性行為.通過(guò)測(cè)試材料在其他方向上的彈性模量,驗(yàn)證了材料的彈性模量預(yù)測(cè)公式的準(zhǔn)確性.通過(guò)對(duì)比理論預(yù)測(cè)結(jié)果和實(shí)驗(yàn)測(cè)試結(jié)果發(fā)現(xiàn),基于材料各向同性假設(shè)得到的理論結(jié)果和各向同性條件不再準(zhǔn)確,在預(yù)測(cè)與設(shè)計(jì)熔絲制造點(diǎn)陣結(jié)構(gòu)的力學(xué)性能時(shí)不能忽略材料的各向異性.通過(guò)本文提供的設(shè)計(jì)方法,對(duì)于部分點(diǎn)陣結(jié)構(gòu),即使材料是各向異性的,也能夠?qū)崿F(xiàn)它們的彈性各向同性設(shè)計(jì).本文的研究對(duì)增材制造聚合物材料各向異性本構(gòu)模型的建立,以及增材制造點(diǎn)陣結(jié)構(gòu)的各向同性設(shè)計(jì)或各向異性控制有一定的參考價(jià)值.

