基于中值預測的四輪嵌入可逆信息隱藏算法
任 方,薛斐元,姚雪梅
(1.西安郵電大學 網絡空間安全學院,西安 710121;2.無線網絡安全技術國家工程實驗室,西安 710121)
0 概述
近年來,隨著互聯網的快速發展,數據傳輸的安全性在各個領域受到廣泛關注。信息隱藏是指將秘密數據隱藏在多媒體文件(如圖像)中,使嵌入的秘密信息不容易被檢測出[1],信息隱藏的主要技術有隱寫術[2-4]、數字水印[5-7]等。大多數的傳統信息隱藏算法可以保證完整的嵌入并提取出秘密數據,但不會考慮數據提取后對原始圖像造成的永久性失真,這在某些對原始圖像有嚴格要求的領域是不能接受的。為了解決這一難題,研究人員提出可逆信息隱藏算法[8],該類算法可以在提取秘密數據后無失真地恢復出原始圖像,目前已被廣泛使用。良好的可逆信息隱藏算法必須具備嵌入容量大、失真率低這2 個重要條件,但這2 個條件之間相互沖突,當嵌入較多數據時會導致更多的像素值發生變化,造成偽裝圖像高失真,反之亦然。因此,研究在同等嵌入容量下具有較低失真率的可逆信息隱藏技術,具有重要的理論意義和使用價值。
早期的可逆信息隱藏算法主要基于無損壓縮[9]來實現,這種算法的嵌入容量有限,且算法性能取決于壓縮算法的優劣,應用范圍較窄。TIAN[10]在2003 年提出基于差值擴展的可逆信息隱藏算法,該算法通過將2 個相鄰的像素產生的差值擴大2 倍,從而嵌入一個數據位,因此,其最大嵌入容量可以達到0.5 bpp。李傳目等[11]通過擴展相鄰3 個像素值與其均值的差值來嵌入數據,其最大嵌入容量從0.5 bpp提升到0.66 bpp。蘇文桂等[12]提出雙層差值擴展,其更好地利用了像素之間的相關性,在高嵌入率下可以保證較低的失真率。LI 等[13]提出一種基于預測誤差擴展的方法,該方法可以有效降低圖像的失真率。與無損壓縮相比,差值擴展具有更大的嵌入容量。
NI 等[14]在2006 年提出一種基于直方圖平移的可逆信息隱藏算法,該算法移動圖像灰度直方圖峰值點與零點之間的像素點以留出空余位置,通過修改峰值點像素值進行數據嵌入,由于每個像素值最多變化1,因此其具有較小的失真率。隨后,出現了許多基于直方圖平移技術的改進算法[15-16]。LEE 等[15]提出利用圖像差值直方圖進行可逆信息隱藏的方法,與NI 等的灰度直方圖移位相比,差值直方圖的形狀更加陡峭,峰值點較高,因此,能實現更高的嵌入容量。WANG 等[16]提出一種基于多個直方圖平移進行數據嵌入的通用框架,使用該框架可以大幅提高嵌入容量。
THODI 等[17]在2007 年提出一種基于預測誤差擴展的可逆信息隱藏算法,與普通的誤差擴展相比,該算法利用預測誤差進行擴展嵌入,更好地利用了相鄰像素點之間的局部相關性。隨后,研究人員在此基礎上做出多方面的改進。TSAI 等[18]將預測誤差擴展技術引入到直方圖平移算法中,利用相鄰像素的相關性預測來解決直方圖平移算法嵌入容量低的問題。SACHNEV 等[19]提出菱形預測算法,該算法將圖像劃分為類似于棋盤格的2 個互不相交的集合,其中一個集合用于預測,另一個集合用于數據嵌入,從而實現雙層嵌入,提高了算法的嵌入容量。CHEN 等[20]提出一種非對稱直方圖平移的可逆信息隱藏算法,該算法減少了無效移位點個數,降低了偽裝圖像的失真率。WENG 等[21]提出像素值排序的可逆信息隱藏算法,該算法首先對圖像進行分塊,然后對塊中剩余像素作排序,選擇3 個最大以及最小的像素值點進行數據嵌入,最高可在每2 個像素點中嵌入一位數據,提高了嵌入容量。HUANG 等[22]在生成誤差直方圖后首先將大于峰值點的像素向右移位,當嵌入數據后再次生成誤差直方圖并向左移位,從而實現了雙層嵌入,改善了嵌入容量不足的問題。
本文提出一種基于預測誤差直方圖平移的可逆信息隱藏算法,該算法利用中值預測生成預測誤差直方圖,在嵌入數據時采用四輪嵌入的模型提高算法的嵌入容量。在平移預測誤差直方圖時,基于每個像素點的復雜度對預測誤差進行排序,優先在圖像平滑區域嵌入數據,減少只用于移位而不進行嵌入的無效移位像素點的個數,從而解決圖像失真的問題。
1 基礎理論
本節以NI 等[14]和TSAI 等[18]所提算法為例,詳細闡述基于灰度直方圖平移與基于預測誤差直方圖平移進行數據嵌入的過程。
1.1 灰度直方圖平移算法
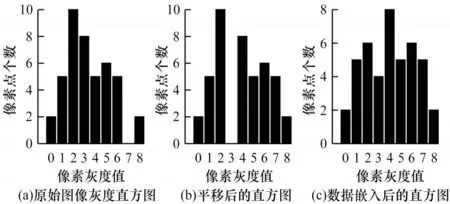
灰度直方圖平移算法首先掃描整幅圖像生成像素灰度直方圖,然后在直方圖中找到一對峰值點與零點,在數據嵌入時,將峰值點與零點之間的像素平移一個單位以留出空位,當要嵌入的數據位是“1”時,峰值點像素平移一個單位,當要嵌入的數據位是“0”時,峰值點像素保持不變。設a、b分別為峰值點與零點,且a 其中:x(i,j)是原始載體圖像的像素值;y(i,j)是移位后的偽裝圖像像素值;m∈{0,1}為待嵌入的秘密數據。 圖1(a)所示為原始圖像灰度直方圖,其中,a=2,b=7;圖1(b)與圖1(c)分別是平移與數據嵌入后的直方圖。從中可以看出,最壞情況下每個像素點的灰度值變化1 個單位,即均方誤差最大為1,對于一幅512×512 像素的灰度圖,可以計算出峰值信噪比(PSNR)最小為48.13 dB,因此,在數據嵌入后可以得到與原始載體圖像視覺效果相近的偽裝圖像。此外,在提取端只需將灰度直方圖按照相反的位置移位,即可恢復原始圖像。 圖1 灰度直方圖的平移與嵌入過程Fig.1 Translation and embedding process of gray histogram 對于一副尺寸為M×N的灰度圖像I,將其劃分為大小為m×n的圖像塊,在每個圖像塊中用多個像素點線性預測一個像素點的像素值,具體嵌入過程如下: 1)對于每個圖像塊,用原始像素值減去預測像素值來計算預測誤差。通過收集所有的預測誤差e∈[?255,255],可以構造出圖像的預測誤差直方圖h(e)。 2)在得到預測誤差直方圖h(e)后,先將其按照正負劃分為h(e+)、h(e?)2 個部分,其中,e+∈(0,255),e?∈(?255,?1),然后在2 個區間內各找出一對峰值點和零點(p+,z+)、(p?,z?)。 3)將(p+,z+)區域內的預測誤差向右移,(p?,z?)區域內的預測誤差向左移,留出空余位置,然后根據秘密數據b∈{0,1}在峰值點進行數據嵌入。 4)每個塊都以相同的方式進行處理,在處理完所有塊后,利用修改過的預測誤差加預測像素值得到偽裝圖像。 在提取與恢復階段,只需將預測誤差直方圖按照相反的位置移位,即可恢復原始圖像。該算法分別在h(e+)和h(e?)中找到峰值點和零點進行嵌入,因此,在不考慮位置信息的情況下,其嵌入容量等于p++p?。 上述2 種算法均存在2 個缺陷:其一是沒有充分考慮相鄰像素的相關性,直方圖的峰值點像素較少,算法嵌入容量較低;其二是按照像素的空間位置進行順序嵌入,沒有考慮圖像的局部平滑度,導致無效移位點(即只進行移位而不進行數據嵌入的像素點)過多,灰度值變化的像素點較多,均方誤差較大,圖像失真較高。如果能優先在圖像的平滑區域嵌入數據,偽裝圖像與原始圖像之間的差異就會減小,因為平滑區域有較少的無效移位點。因此,合理設計預測方式,同時根據像素復雜度優先在平滑區域嵌入數據,對于增大嵌入容量和減小偽裝圖像失真率都會有一定的改善效果。 如前文所述,嵌入容量與預測誤差直方圖峰值點處的像素點數目密切相關,當直方圖越趨近于陡峭時,意味著峰值點越多,嵌入容量也越大。為了改善預測誤差直方圖平移算法的性能,本文充分考慮相鄰像素的相關性,提出一種基于中值預測誤差的四輪嵌入算法。該算法采用圖像劃分集合和中值預測的方法進行像素值預測,其中,劃分的集合互不相交,預測時集合之間互不影響,可以無損地恢復原始圖像。中值預測的優勢在于利用相鄰像素點的灰度值對中心點像素進行預測,預測值更為準確,生成的預測誤差直方圖峰值點個數更多,增大了嵌入容量,由于圖像像素總數是固定的,因此減少了無效移位像素點。上述2 種方法相結合,利用中值預測方法計算當前集合中像素點的預測值時,使用的像素點來自其他集合,與當前集合的其他點無關,方便進行無損恢復。此外,本文算法還根據每個像素點的復雜度對預測誤差進行排序,優先在圖像平滑區域嵌入數據,從而進一步減少無效移位像素點,降低由于數據嵌入所導致的均方誤差以及偽裝圖像的失真率,從而實現更好的嵌入效果。 本文算法將圖像中的所有像素點分為4 個互不相交的集合,記為A、B、C、D,如圖2 所示。嵌入過程分為四輪進行,每一輪使用其中一個像素點集合嵌入秘密信息的1/4,具體預測過程為:使用鄰近的8 個像素點預測中心點像素,如預測A集合的點xi,j時使用相鄰的B、C、D集合的點。該方法的優勢在于充分考慮了鄰近像素之間的相關性,使預測值更為準確,生成的預測誤差直方圖可以在誤差較小的點處聚集大量像素,大幅提升了嵌入容量,如圖3 所示。 圖2 四輪嵌入模型Fig.2 Four-round embedded model 圖3 本文算法的預測誤差直方圖Fig.3 The prediction error histogram of this algorithm 目前大多數預測誤差直方圖平移算法都是按照固定順序來掃描像素從而進行秘密數據嵌入,并沒有考慮圖像的紋理信息。本文為圖像中的每個像素點定義復雜度,按照像素點復雜度進行排序,從復雜度低的點處開始嵌入數據,該方法優先在圖像平滑區域嵌入信息,使原始圖像與偽裝圖像的差異更小,從而減少了無效移位像素點個數。 對于一個尺寸為M×N的圖像,首先將其分為4 個互不相交的集合,然后進行中值預測,具體預測過程如圖4 所示。 圖4 中值預測過程Fig.4 Median prediction process 在不考慮邊界上的像素時,每個集合的預測方式是相同的,以集合A為例,在第一次嵌入數據時,集合A用于數據嵌入,剩余3 個集合用于對集合A進行預測。具體步驟如下: 1)分別抽取除中心點像素xi,j外的8 個鄰近像素(xi?1,j?1,xi?1,j,xi?1,j+1,xi,j?1,xi,j+1,xi+1,j?1,xi+1,j,xi+1,j+1),并將其按照升序排列為。 2)對于xi,j,其預測值為該序列最中間2 個像素值的平均值med: 預測誤差為: 3)按照上述步驟對圖像剩余的集合A像素點進行處理。 根據預測誤差直方圖可以將像素點分為嵌入點和平移點2 個部分。只進行平移的點是無效移位點,它不會影響實際嵌入容量的大小,但當其數量較多時會導致PSNR 降低,原始圖像與偽裝圖像的差異過大。因此,根據圖像平滑程度對每個像素點定義復雜度,根據復雜度對預測誤差進行排序,在低嵌入率下可以減少無效移位點的個數,提升PSNR 值。不同的復雜度判斷標準會對低嵌入率下的PSNR 產生一定影響,本文給出一種復雜度計算方法。為了完整恢復原始圖像,像素點復雜度應具備如下2 個特征: 1)該值不能在嵌入數據后發生變化。 2)當像素點復雜度較小時,預測誤差絕對值也應該較小,反之亦然。 本文算法中的4 個集合是相互獨立的,意味著一組集合中的像素值變化不會影響到另一組集合,反之亦然。預測集合A中的點xi,j使用了其余3 個集合的灰度,這些灰度在嵌入前后不發生變化,因此,復雜度也應該由它們進行計算。本文根據相鄰像素之間的相關性將它們各自的局部差值定義為像素xi,j的復雜度,當該復雜度較小時,預測誤差一般也較小。將中心點與鄰近8 個像素點做灰度差,然后計算這些灰度差與平均灰度差的偏離程度并將其作為中心點的復雜度,復雜度越小,中心點鄰域的灰度值變化越小,圖像局部區域越平滑,反之則越粗糙。復雜度的具體計算公式如下: 其中: 嵌入過程具體如下: 1)根據B、C、D這3 個集合獲取集合A中所有像素的復雜度和預測誤差,將復雜度按升序排序以獲得序列(fA1(i,j),fA2(i,j),fA3(i,j),…),并通過復雜度中的順序對預測誤差進行排序,得到(eA1(i,j),eA2(i,j),eA3(i,j),…)。 2)生成預測誤差直方圖,找出2 對峰值點與零點(p1,z1)、(p2,z2)(這里的零點是指誤差值出現次數為0 的點),p1、p2分布在直方圖中間區域,z1、z2分布在直方圖兩端區域。 3)將1/4 的秘密數據分配給集合A。依次掃描預測誤差序列(eA1(i,j),eA2(i,j),eA3(i,j),…)并按照式(5)修改預測誤差,實現數據嵌入。 其中:b是要嵌入的秘密數據,b∈{0,1};為修改后的預測誤差。因此,偽裝圖像的像素值可由下式計算: 其中:yi,j為偽裝圖像的像素值。 4)根據上述步驟完成集合A的數據嵌入,以同樣的方式分別進行集合B、C、D的數據嵌入。 提取與恢復是嵌入的逆向過程,在嵌入時是從集合A到集合D,在提取和恢復時則需要從集合D開始。首先,從集合D中提取嵌入的秘密數據并恢復D,然后分別在C、B、A上做同樣的操作。由于4 個集合互不相交,在恢復原始圖像像素值時使用的預測值與嵌入時使用的預測值完全一樣,因此可以無損恢復出原始圖像。提取與恢復的具體流程如下: 1)計算偽裝圖像中集合D所有像素的預測誤差和復雜度。注意到集合D中像素的復雜度是基于嵌入后的集合A、B、C而計算的,它的值與嵌入D之前相同,因此,升序排列后的復雜度序列和預測誤差序列的順序與嵌入時相同。 2)提取秘密信息。按照式(7)依次從預測誤差序列(eD1(i,j),eD2(i,j),eD3(i,j),…)中提取嵌入的秘密數據: 這里的兩對峰值點和零點(p1,z1)、(p2,z2)與嵌入時相同。 3)恢復原始圖像。在提取所嵌入的秘密數據的過程中,原始圖像的恢復如下: 相應地,原始像素值可由式(9)恢復: 4)在集合D提取和恢復完成后,以D為基礎,利用同樣的操作完成集合C、B、A的提取和恢復,直至整個原始圖像完全恢復。 當p1>p2、z1>z2時,預測誤差直方圖的移位情況如圖5 所示。 圖5 本文算法的嵌入、提取與恢復過程Fig.5 The embedding,extraction and recovery process of the algorithm in this paper 在預測誤差直方圖的移位過程中可能存在上溢或下溢的問題,導致原始圖像的部分點恢復不具備可逆性,因此,需要對原始圖像進行預處理。首先,由于本文使用四輪嵌入模型,因此邊界位置的像素值(即圖像邊界上、下、左、右4 列)不在考慮范圍之內;其次,對于像素值為0 或255 的點,左移或右移會導致原始圖像永久性失真,因此,需要將其記錄下來,在嵌入時不使用這些點,將其位置信息作為附加信息并與秘密信息一起進行嵌入。在恢復時,首先根據附加信息找到那些未使用的點,然后將其排除在外,在提取秘密信息和恢復載體時不對這些點進行操作。 本次實驗選用6 張來自USC-SIPI圖像數據庫且尺寸為512×512 像素的標準測試圖像,分別為Lena、Baboon、Airplane、Boat、Elaine、Man,如圖6所示。從PSNR和嵌入能力2個方面,將本文算法與非對稱直方圖算法[20]、像素值排序算法[21]以及誤差直方圖移位算法[22]進行比較。此外,為了降低隨機選擇測試圖像所造成的影響,分別對該數據庫中的30幅灰度圖像進行平均結果測試。 圖6 測試圖像1Fig.6 Test images 1 由于4 種對比算法本質上都是利用預測誤差直方圖在峰值點嵌入數據,因此在不考慮附加信息的情況下,嵌入數據的位數等于峰值點像素個數。本文以嵌入率EEC作為衡量標準,EEC表示每個像素點最多可以嵌入多少位數據。對于一幅尺寸為512×512 像素的測試圖像,最大嵌入率的計算公式如下: 其中:pmax為預測誤差直方圖中峰值點像素個數。由于本文使用四輪嵌入的模型,因此最大嵌入率為: 圖7 所示為4 種算法在6 幅測試圖像中的最大嵌入容量情況。從圖7 可以看出,本文算法具有較高的嵌入能力。在測試圖像Lena 中,本文算法最多可嵌入63 832 位數據,嵌入率高達0.24 bpp,比其他3 種算法分別高出0.08 bpp、0.02 bpp、0.11 bpp。在紋理相對粗糙的圖像Baboon 中,本文算法的嵌入率為0.07 bpp,雖然相較其他圖像下降了很多,但是仍然分別高出其他3 種算法0.018 bpp、0.020 bpp、0.010 bpp。在紋理相對平滑的圖像Airplane中,本文算法嵌入率高達0.36 bpp,遠高于其他3 種算法。本文采用四輪嵌入的模型,用中心點像素周圍的8 個像素點做預測,預測值較3 種對比算法更為準確,峰值點像素更多。此外可以看出,非對稱直方圖算法在部分圖像中的嵌入容量和本文算法之間差距很小,這是因為該算法采用不對稱預測誤差直方圖將直方圖分成正、負2 個部分,可以實現雙層嵌入。 圖7 4 種算法的最高嵌入率對比Fig.7 Comparison of highest embedding rate of four algorithms PSNR 通常用來衡量圖像質量,其能反映原始圖像與偽裝圖像之間的相似程度,PSNR 值越高,說明偽裝圖像與原始圖像之間越相似。在計算PSNR時,首先要計算圖像的均方誤差,用MSE 表示原始圖像與偽裝圖像之間的均方誤差。對于一副尺寸為512×512 像素的測試圖像,MSE 定義為: 其中:xi,j為原始圖像像素值;yi,j為偽裝圖像像素值。PSNR 的計算公式為: 圖8所示為同等嵌入容量下各算法的PSNR對比。 圖8 同等嵌入容量下的PSNR 對比Fig.8 Comparison of PSNR under the same embedding capacity 從圖8 可以看出,在同等嵌入容量的情況下,本文算法PSNR 性能明顯高于另外3 種算法。在紋理相對粗糙的測試圖像Baboon 中,當嵌入容量是5 000 bit 時,本文算法的PSNR 為60.08 dB,比3 種對比算法分別高出0.12 dB、0.92 dB、0.62 dB。在紋理相對平滑的測試圖像Airplane 中,3 種對比算法的PSNR 雖然都很高,但是本文算法仍然優于3 種算法,如在嵌入容量為5 000 bit 時,本文算法的PSNR可達65.78 dB。本文使用中心像素鄰近8 個像素的中位數進行預測,預測值更為精準,此外,在嵌入端根據每個像素點的復雜度對預測誤差序列進行排序,在圖像相對平滑的區域優先嵌入數據,在同等的嵌入容量下大幅減少了無效移位的像素點個數,降低了均方誤差,提高了PSNR,因此,本文算法的嵌入質量明顯高于3 種對比算法。 如圖9 所示,本文分別對USC-SIPI 圖像數據庫中的30 幅尺寸為512×512 的灰度圖像進行平均結果測試,其中,最大嵌入率及對應的PSNR 值如表1 所示,當嵌入容量為0.1 bpp 時的PSNR 如表2 所示。從表1可以看出,本文算法的平均最大嵌入率為0.30 bpp,而其他3 種算法的平均最大嵌入率分別為0.15 bpp、0.16 bpp、0.13 bpp,本文算法分別提高了0.15 bpp、0.14 bpp、0.17 bpp。從表2 可以看出,本文算法在嵌入率為0.1 bpp 時PSNR 平均值為55.15 dB,相較非對稱直方圖算法提高了0.61%,相較誤差直方圖平移算法提高了0.7%,相較像素值排序算法提高了0.62%。 圖9 測試圖像2Fig.9 Test images 2 表1 最大嵌入率及對應的PSNRTable 1 Maximum embedding rate and its corresponding PSNR 表2 嵌入率為0.1 bpp 時的PSNRTable 2 PSNR at embedding rate of 0.1 bpp dB 根據上述實驗結果可以得出,本文算法對于典型灰度圖像具有較好的效果,能夠在完整提取秘密信息后無失真地恢復原始圖像,且具有較高的嵌入容量和偽裝性,這是因為本文算法采用了四輪嵌入的模型,每一次都使用中心像素周圍的8 個像素灰度值排序后進行中值預測,由于這些像素點位置相鄰,因此灰度值具有較強的相關性,得到的預測值較其他算法更為準確,預測誤差直方圖的峰值點像素更多,在嵌入率方面有較大優勢。同時,這種精確的預測方法也使嵌入數據時需要進行無效移位的像素點個數大幅減少,從而提升了PSNR 值。 本文算法的另一個優勢是對每個像素點定義了復雜度,根據復雜度高低來掃描預測誤差,優先在圖像平滑區域嵌入數據,有效降低了偽裝圖像的失真率,進一步提升了PSNR 值,得到的偽裝圖像視覺質量更好。此外,本文算法雖然是四輪嵌入,但是對于每個像素點只需進行一次預測,且預測的主要過程是少量相鄰像素值排序,耗時較小,算法的執行效率較高。與其他算法相比,本文算法的計算復雜度沒有明顯提高,因此,具有較強的實用性和適用性。 為了增大嵌入容量并提升偽裝圖像的視覺質量,本文提出一種基于中值預測的可逆信息隱藏算法。該算法將圖像劃分為4 個互不相交的集合并分層嵌入數據,在利用某一集合進行嵌入時,通過其他3 個集合的像素點中值進行預測,由于圖像各個像素點之間具有一定的相關性,因此生成的預測誤差直方圖更加陡峭,可以實現較高的嵌入容量。此外,本文在嵌入數據時,根據每個像素點的復雜度對預測誤差進行排序,優先在像素平滑區域嵌入數據,從而大幅減少無效移位像素點,降低由于數據嵌入所導致的均方誤差,最終提高峰值信噪比。實驗結果表明,本文算法具有較大的嵌入容量,且在同等嵌入容量下,其PSNR 較對比算法更高。本文算法在一定程度上提升了可逆信息隱藏性能,但僅限于以灰度圖像作為載體的情況。彩色圖像三通道之間同樣存在較強的相關性,充分利用彩色圖像自身的特點設計一種比傳統算法更優的可逆信息隱藏算法,將是本文下一步的研究方向。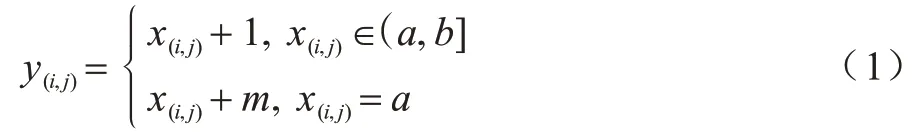
1.2 預測誤差直方圖平移算法
2 本文算法
2.1 算法思想


2.2 中值預測



2.3 復雜度計算

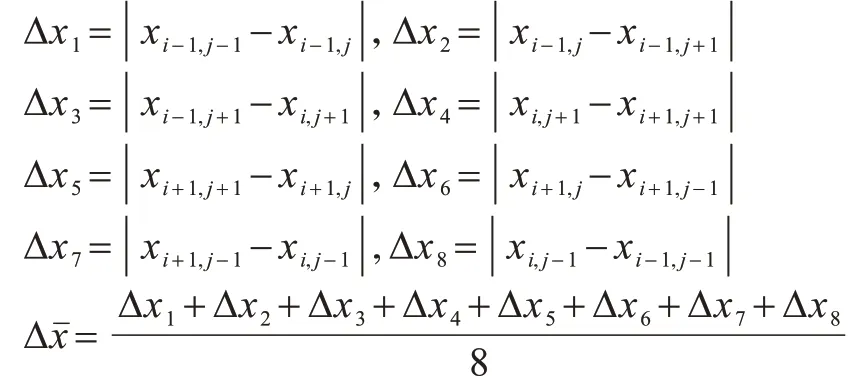
2.4 嵌入過程
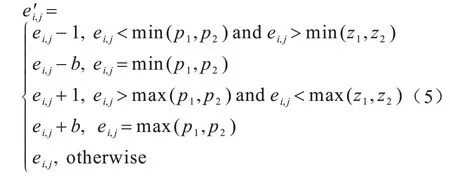

2.5 提取與恢復過程
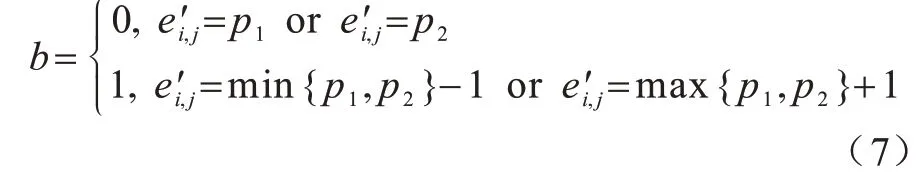


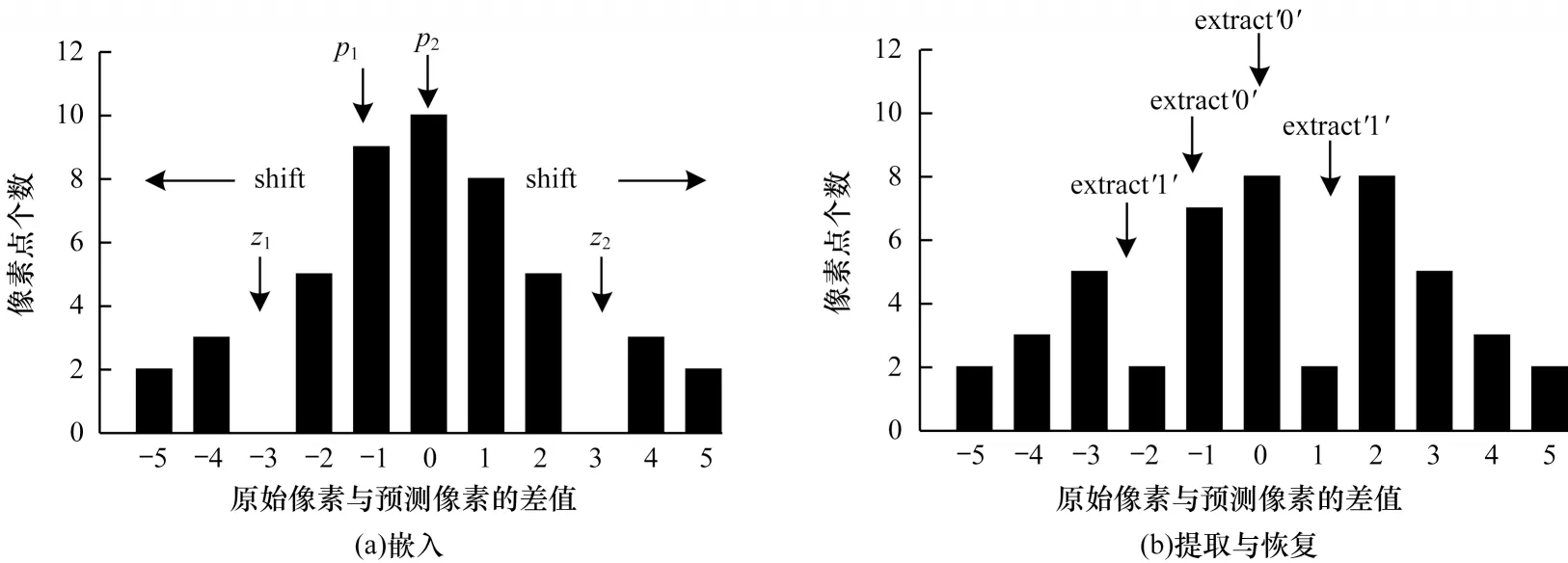
2.6 上溢和下溢問題處理
3 實驗結果及分析

3.1 嵌入容量對比



3.2 PSNR 對比






3.3 結果分析
4 結束語

