基于系數搜索的振動補償方法*

要佳敏 莊偉 馮金揚 王啟宇 趙陽 王少凱 吳書清 李天初

(中國計量科學研究院,北京 100029)

1 引言

絕對重力測量,即對重力加速度絕對值的精確測量,在輔助導航、資源勘探、地球物理、計量領域都有著廣泛的應用[1-4].現有的高精度絕對重力儀普遍采用自由落體法,主要包括以角錐棱鏡為下落物體的激光干涉式絕對重力儀[5-8]和以冷原子團為下落物體的原子干涉式絕對重力儀[9-14],以下分別簡稱為光學重力儀和原子重力儀.前者通過激光干涉儀測量角錐棱鏡在真空中自由下落的運動軌跡,擬合求解重力加速度,后者根據原子團在自由下落的過程中經過3 次拉曼激光脈沖作用形成的原子干涉條紋來計算重力加速度.由于二者的實際測量對象是下落物體或下落原子團相對于儀器內一個參考鏡(角錐棱鏡或平面鏡)的運動加速度,因此參考鏡自身的加速度必然耦合到測量結果中.理論上,忽略參考鏡自身振動時,現有的絕對重力儀的測量精度可以達到微伽(μGal,1 μGal=1 ×10—8m·s—2)量級;但實際上,如果直接將參考鏡放置在地面上,地面振動引起的測值離散度將超過10 μGal,在復雜振動環境中甚至達到mGal 或10 mGal 量級.因此,利用測振儀器獲得參考鏡自身的運動加速度并在計算重力加速度時對其影響進行修正是提高絕對重力儀測量精度的有效手段之一,這種修正方法一般稱為振動補償.

具體而言,影響原子重力儀的地面振動噪聲主要為環境噪聲,與測量時間和測量點的地基、坐標及環境有關,可以根據頻率來粗略區分.首先是人類活動噪聲,一般大于1 Hz,如儀器測試期間附近的人員走動,車輛等人工振源產生的振動,以及建筑物的晃動等.其次是來自地球本身的噪聲,一般在0.1—1.0 Hz 之間,主要包括周期性的脈動和地震等地球內部運動引起的振動,其中地脈動噪聲模型的加速度功率譜密度在頻率為0.2 Hz 和3.0 Hz的位置存在峰值[15].最后是氣壓波動等大氣運動噪聲,一般小于0.1 Hz,普遍變化緩慢且幅值較低,對絕對重力測量的影響可以忽略[16,17].由于絕對重力測量只依靠垂直方向的位移數據進行計算,因此對原子干涉條紋進行振動補償時,一般忽略地面振動的水平分量,僅需使用測振儀器輸出的垂直振動信號.

目前國際上較為成熟的原子重力儀是法國巴黎天文臺研制的CAG-01 型原子重力儀,曾參加過多次國際重力比對,采用的振動處理方法為被動式垂直隔振系統與振動補償的結合,其中振動補償的具體原理為:數據采集卡同步記錄原子干涉過程中的地震計輸出的速度信號與原子干涉條紋,在控制軟件中利用無限沖激響應(infinite impulse response,IIR)濾波器和非因果低通濾波器對地震計信號進行處理,以減小地震計傳遞函數幅頻特性不恒定、相頻特性存在非線性的影響,獲得更真實的參考鏡振動信號,最后利用處理后的信號得到由參考鏡振動引入的相位噪聲,修正原子干涉條紋.在該儀器所在的測量環境中,此振動補償方法本身可以使重力儀靈敏度提升為原來的3 倍[11].德國漢諾威大學提出利用數字式低通和高通濾波器對振動傳感器的輸出信號進行前處理,以得到更為精確的參考鏡振動引入的相位噪聲,從而實現振動補償.其實驗結果表明,在較安靜的環境中利用高精度商用地震計進行振動補償,或在復雜振動環境中使用精度較低的商用加速度計或其自主研制的新型光學慣性傳感器進行補償,均可以有效提高重力儀的靈敏度[18].在我國,浙江大學自制的原子重力儀同樣采用了振動補償方法,其主要特點為利用商用反演軟件修正地震計實測傳遞函數的影響以獲得更真實的參考鏡振動信號.在其實驗室環境中,該方法可以將重力儀的靈敏度提升至與使用被動隔振系統時相近的水平[19].國防科技大學對參考鏡垂向振動及水平偏轉引入的測量噪聲進行了詳細分析,利用加速度計測量原子重力儀工作時的參考鏡振動,同時對加速度計與參考鏡之間的傳遞函數進行了較為精確的標定.實測結果表明在較復雜的振動環境中其振動補償方法可以實現顯著的振動補償效果[20].軍事科學院國防創新院提出的振動補償方法則采用具有高精度四通道移相探測器的邁克耳孫激光干涉儀替代傳統振動傳感器.該干涉儀可以直接測量出原子干涉條紋的相移,并結合信號整形、數字鑒相等方法確定拉曼激光脈沖作用前后原子干涉條紋的相位小數的變化,得到參考鏡振動引起的原子干涉相位偏差.去除該相位偏差,即可對重力儀測量到的躍遷概率信號進行修正[21].此外,中國計量科學研究院、中國科學院精密測量研究院、華中科技大學、中國科技大學、國防科技大學、美國斯坦福大學、德國洪堡大學等單位也研制了不同類型的隔振系統[12,13,22-26],以減小地面振動對原子重力儀的影響.

德國漢諾威大學的Richardson 等[18]和我國國防科技大學的研究人員[20]均指出,傳統振動傳感器與參考鏡由于安裝位置不同形成的機械傳遞函數可能是影響振動補償精度的重要因素;在原子重力儀進行正式測量前對該傳遞函數中的關鍵系數進行初始標定有助于提高振動補償效果.這些分析為提升原子重力儀的振動補償精度提供了重要指導,但目前尚無具有普適性的、能夠在任意測量時間及地點快速實現對傳遞函數進行實時修正的具體振動補償算法.而在光學重力儀方面,清華大學的研究人員給出了對重力測量結果進行實時修正的基于相同簡化模型的具體振動補償算法,并提供了該算法在不同地點對延時系數和增益系數進行實時計算的結果及重力測量的實測結果[27-29].他們采用的傳感器為高精度地震計,利用相關分析法或黃金分割法搜索出當前環境下這2 個系數的具體值,并對下落物體軌跡信號進行修正.對同一套振動補償算法,輸入在中國計量科學研究院昌平院區的安靜環境中測得的重力數據和地震計數據,算法的直接輸出結果表明振動補償后光學重力儀的測量分辨率可以提升5 倍;輸入在清華大學所處的復雜振動環境中的數據,結果表明振動補償可將重力儀的測量分辨率提升16 倍,效果更為顯著[27].該算法最大的特點是較強的自適應性,在不同時刻和不同地點的測量過程中可以直接使用,以保證真實的機械傳遞函數因環境變化而發生改變時對其當前值進行實時估算,實現當時當地最好的振動補償效果.受上述研究結果的啟發,基于上述簡化模型,本文給出了一套振動補償算法的工作原理和具體流程,該振動補償算法可以應用于原子重力儀，對傳遞函數進行實時標定.我們通過仿真運算對算法的有效性進行了詳細驗證,最后利用實驗室自主研制的原子重力儀實際評估了該算法對原子干涉條紋擬合精度和重力測值離散度的補償效果,為提高原子重力儀在不同環境甚至是復雜振動環境中的測量精度提供幫助.

2 原 理

2.1 應用于原子重力儀的振動補償原理

原子重力儀基于冷原子物質波干涉原理,將激光脈沖作用到冷原子團,通過雙光子受激拉曼躍遷或多光子布拉格衍射過程來實現原子干涉過程[9].以基于受激拉曼躍遷的原子重力儀為例,冷原子團在真空腔中自由下落,真空腔下方的平面參考鏡將垂直向下的拉曼激光原路反射,使兩束對射的激光同時作用于原子團,在此過程中3 個連續的激光脈沖實現了原子波包的分束、反轉和合束,分別為第1 個π/2 脈沖、π 脈沖和第2 個π/2 脈沖,相鄰脈沖的時間間隔為T[30].合束后任一能態的原子均由2 條路徑上的原子疊加而成,通過熒光信號可以探測脈沖作用后原子團的躍遷概率P,即干涉條紋,滿足

式中:ΔФ為原子相位,與當地的重力加速度g有關;代表條紋對比度的系數A和B可以通過對干涉條紋進行余弦擬合得到.理想情況下,原子相位ΔФ等于其理論值ΔФth,即

式中,keff為有效波矢,α表示激光的掃頻速率.重力儀的控制軟件調控 (2) 式中的α線性增大,則原子相位ΔФ也將線性變化,使干涉條紋呈現為標準余弦信號的形式.此時P應與由P擬合出的標準信號Pfit完全相同,有

但實際情況下,受到各種相位噪聲的影響,原子相位ΔФ等于其實際值ΔФm,有

式中Δφvib為參考鏡振動引入的相位噪聲,以下簡稱為振動相位;Δφothers為其他噪聲源引入的相位噪聲的總和,以下簡稱為其他相位噪聲.此時P由Pfit變為

當振動相位在相位噪聲中占主導時,依據上述原理可以確定修正干涉條紋P的振動補償過程.第一步,對原始實測條紋P(ΔФth)進行余弦擬合,得到擬合出的理論條紋Pfit(ΔФth)和(1)式中的系數A和B.需要說明的是,此時可以將原子重力儀在正式測量前的初始測量過程中獲得的粗測值gth代入(2)式以得到擬合條紋Pfit.這是因為原子重力儀到達一個新的測量地點后一般都需要在啟動階段通過改變拉曼間隔T并掃描掃頻速率α來獲得正式測量所用的中心值αcenter,而該測點的粗測重力值即為gth=αcenter/keff.此后每一次或每一組躍遷概率數據都對應真實重力值相對于該粗測值的偏差Δg,所以實際上重力儀最終輸出的高精度測值為g=gth+Δg.因此利用粗測值gth計算擬合條紋有利于提高計算效率,這也符合原子重力儀的一般測試流程[19,20].第二步,通過振動傳感器獲得一段時間t內參考鏡的真實振動速度vm(t),進而根據

計算出真實的振動相位Δφvib,其中S(t)為重力儀的靈敏度函數,T1和T3分別為第1 個π/2 脈沖和第2 個π/2 脈沖的作用時刻,均由重力儀控制軟件的已知參數決定.第三步,計算出僅受振動影響時的原子相位ΔФv和躍遷概率Pv,即

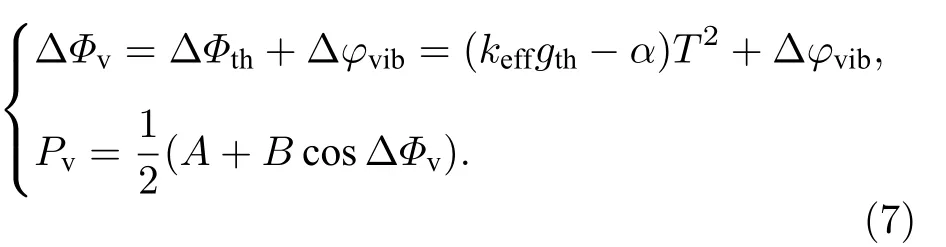
此時重新以ΔФv為橫坐標、P為縱坐標得到的數據對P(ΔФv)即為修正后的干涉條紋,至此補償過程結束.如圖1 所示,與藍色圓圈表示的原始條紋P(ΔФth)相比,紅色方塊表示的修正條紋P(ΔФv)的橫坐標有所移動,理論上應更接近灰色的標準余弦信號,即擬合出的理論條紋Pfit(ΔФth).也就是說,對修正后的條紋P(ΔФv)再次進行余弦擬合時的均方根誤差(root mean square error,RMSE)值應小于對原始條紋P(ΔФth)進行擬合時的RMSE 值.

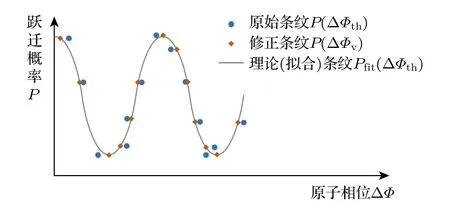
圖1 原子干涉條紋示意圖Fig.1.Schematic diagram of the fringe signal of atomic interferometer.

2.2 基于傳遞函數簡化模型的振動補償方法

基于傳遞函數簡化模型以實現上述振動補償過程的方法包括硬件和軟件兩方面.

硬件方面,由于目前尚無以原子重力儀的參考鏡為敏感質量的地震計,因此一般而言只能用一臺獨立的地震計或加速度計放在參考鏡旁邊或下方測量其振動.然而,受機械結構及地震計自身性能的限制,地震計輸出信號Us(t)并不能完全真實地反映參考鏡的振動速度vm(t),二者的關系如圖2所示,其中Ga表示從地面振動速度到參考鏡振動速度的傳遞函數,Gb表示從地面振動速度到地震計敏感質量振動速度的傳遞函數,Gc表示從敏感質量運動速度到地震計輸出電壓之間的傳遞函數.由于地震計內部的敏感質量與參考鏡的實際位置必然存在水平和垂直差異,因此Ga與Gb不可能相等,且當地基材料改變時,這兩個傳遞函數本身也可能發生變化.另一方面,地震計自身的傳遞函數Gc并非幅頻特性恒定、相頻特性為線性的理想傳遞函數[31],且有可能隨測量時間與環境的改變而發生變化(這是因為溫度、濕度、氣壓等環境參數會對地震計內部的機電模塊參數產生影響,且這些參數可能隨時間發生漂移).綜上,參考鏡的真實振動速度與地震計輸出的電壓信號之間的傳遞函數H滿足

圖2 地震計輸出信號與參考鏡真實振動的關系Fig.2.Transfer function between the vibration of reference mirror and the output signal of seismometer.

因此對傳遞函數H的求解將直接影響振動補償的效果.

雖然實際情況中Ga,Gb,Gc不易測量且可能改變,導致測量人員無法得到總傳遞函數H的精確值,但由于單次重力測量任務中測量環境不會有顯著變化,且測量時間一般不超過24 h,因此可以利用由一個延時系數τ和一個增益系數K組成的簡化模型來估算H,并認為這兩個系數的數值在當前測量過程中保持不變[27].由此可得圖2 的簡化模型為

式中,Ks為地震計的標稱靈敏度,由制造商提供.

理論上當延時系數τ和增益系數K取最接近真實值時,利用地震計輸出電壓Us和(9)式計算出的參考鏡振動速度vm(t)也最接近真實值,對條紋的修正效果最好.因此振動補償可以選取對條紋進行擬合時的RMSE 值作為優化目標,基本思路為:給定τ的取值范圍,遍歷搜索使RMSE 值達到最小值時對應的最優延時系數τopt;再給定K的取值范圍,在設定延時為τopt的情況下,再次遍歷搜索使RMSE 達到最小值時對應的最優增益系數Kopt.最后,在設定延時為τopt、增益為Kopt的情況下,得到修正后的條紋P(ΔФv)及其余弦擬合時的RMSE 值.

由此得到具體的算法流程如圖3 所示,相應的處理程序即為振動補償方法的軟件部分.上述分析中使用的主要物理符號匯總在表1 中.

表1 主要物理符號描述Table 1.Description of main symbols.

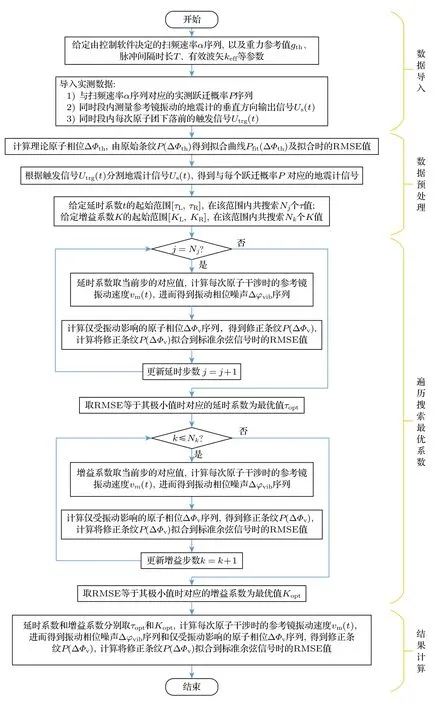
圖3 基于系數搜索的振動補償算法流程Fig.3.The algorithm of the vibration correction method based on element searching.

2.3 振動補償前后干涉條紋擬合殘差的變化

上述振動補償算法的優化目標為擬合干涉條紋時的RMSE 值.該值具有簡單直觀的數學含義,但物理意義不明顯.類比基于相同簡化模型的振動補償方法在光學重力儀中的算法流程[27],可以用另一種更具有物理意義的變量作為振動補償效果的最終評價指標,即干涉條紋擬合殘差的變化.

運行振動補償算法前,先計算出原始條紋P(ΔФth)相較于理論條紋Pfit(ΔФth)的殘差Rm(ΔФth)的標準差σm,即

運行振動補償算法后,利用搜索出的最優延時系數τopt和增益系數Kopt,根據(6)式,(7)式和(9)式得到僅受振動影響的干涉條紋Pv相較于理論條紋Pfit的殘差Rv.同時,記原始條紋P與僅受振動影響的條紋Pv的差值為Rc.顯然Rc也就是原始條紋殘差Rm與僅受振動影響的條紋殘差Rv的差值,相當于去除振動影響后的條紋殘差.理論上振動補償效果越好,則振動相位Δφvib的計算越準確,推算出的僅由振動引入的條紋殘差Rv也越接近原始條紋殘差Rm.此時Rc將趨近于僅由其他相位噪聲Δφothers引入的條紋殘差,其標準差σc也應趨于最小值.因此可以以

相較原始條紋殘差Rm的標準差σm的衰減程度作為衡量振動補償效果的最終指標.

3 仿真驗證

上述振動補償算法的效果將在實驗室自主研發的NIM-AGRb-1 型原子重力儀[12]上進行考察.實際測量之前,可以利用美國 MathWorks 公司生產的 MATLAB 軟件驗證算法的有效性,具體的仿真流程為:1) 參考NIM-AGRb-1 型重力儀的控制參數和之前的實測數據,給定合理的計算參數值,包括波矢keff、粗測重力值gth、靈敏度函數S(t)、拉曼激光的脈沖間隔T=80 ms、1 min 內線性增大的掃頻速率序列α(時間間隔為2 s,相當于原子團的下落間隔)、決定干涉條紋對比度的系數A和B等;2) 給定1 min 內代表隨機振動的速度信號的幅值Arand和代表地脈動的速度信號的頻率序列fs及相應的幅值序列As,具體取值參考地脈動噪聲功率譜密度的新高噪聲模型 (new high noise model,NHNM)[15],設定參考鏡真實振動速度信號vm(t)為這些信號的總和;3) 根據(6)式計算參考鏡振動引入的真實相位噪聲Δφvib,再根據(4)式和(5)式計算其他相位噪聲Δφothers為0 時的躍遷概率Psim,該概率Psim即代表原子重力儀輸出信號P的仿真值,數據量N=30,如圖4(a)所示;4)設定真實延時系數τset=5 ms,真實增益系數Kset=0.9,設定地震計靈敏度Ks為將在實測中使用的CMG-3 ESP 型地震計的靈敏度,根據(9)式反推出此時地震計敏感質量的振動速度和地震計輸出電壓的仿真值vs(t)和Us(t),注意Us(t)即代表地震計在原子重力儀工作時同步輸出的信號,如圖4(b)所示;5)對上述仿真出的概率Psim和地震計電壓信號Us(t)運行振動補償算法.

圖4 (a) 仿真干涉條紋;(b) 仿真振動信號Fig.4.(a) The simulated fringe signal;(b) the simulated output of seismometer.

記以上仿真過程為第1 種情況,運算結果如圖5 和圖6 所示.可以看出,不考慮其他相位噪聲時,該算法可以精確地搜索出設定的延時系數τ=5 ms 和增益系數K=0.9(如圖中黑色虛線所示,下同),并將原始條紋Psim(ΔФth)調整為更接近理論條紋Pfit(ΔФth)的修正條紋Psim(ΔФv),其中典型的修正位置用橘色圓圈標出.補償前對原始條紋Psim(ΔФth)進行余弦擬合時的RMSE 值為13.1×10—3,而補償后對修正條紋Psim(ΔФv)進行余弦擬合時的RMSE 值僅為0.02×10—3.同時該算法計算出的僅受振動影響的條紋相對于理論條紋的殘差Rv(ΔФth)和原始條紋相對于理論條紋的殘差Rm(ΔФth)完全相同.依據2.3 節提出的評價指標,此時原始條紋殘差Rm的標準差σm為12.39×10—3,而去除振動影響后的條紋殘差Rc的標準差σc僅為0.02×10—3,衰減幅度達到99.8%,驗證了該振動補償算法的有效性.

圖5 其他相位噪聲為0 時仿真得到的擬合RMSE 值與(a)延時系數和(b)增益系數的關系Fig.5.The RMSE value of fringe fitting as a function of (a) time delay and (b) proportional element,without considering other phase noises,calculated by simulation.

圖6 其他相位噪聲為0 時仿真得到的(a)修正前后的干涉條紋與理論擬合曲線(典型修正點用橘色圓圈標出),(b)原始條紋的擬合殘差與計算出的僅由振動導致的條紋的擬合殘差Fig.6.(a) The simulated fringe signals before and after vibration correction with the fitted curve as the reference (with the typical corrected data marked by orange circles),and (b) the fitting residual of the simulated fringe signals,without considering other phase noises.

進一步,修改前述仿真流程的第3 步,設定其他相位噪聲Δφothers為±10 mrad 范圍內的隨機值.這種設定可以更準確地模擬實際測量,記該仿真過程為第2 種情況.此時雖然振動相位Δφvib的范圍約為±400 mrad,是其他相位噪聲Δφothers的40 倍,但仿真運算結果表明其他相位噪聲的干擾仍不可忽視.如圖7 和圖8 所示,此時算法搜索出的延時系數為τ=2.7 ms,與設定值的區別達到毫秒量級;增益系數為K=0.957,與設定值相比偏大6.3%.此時雖然該算法同樣可以將原始條紋Psim(ΔФth)調整為更接近理論條紋Pfit(ΔФth)的修正條紋Psim(ΔФv)(典型位置如橘色圓圈所示),但偶爾會因設定為隨機值的其他相位噪聲Δφothers而產生隨機運算誤差,如綠色方框所示的數據被修正到理論條紋曲線的另一側而不是曲線上;計算出的僅由振動引入的條紋殘差Rv(ΔФth)和原始條紋殘差Rm(ΔФth)大致相同,但也存在一定差異.最后,此時原始條紋殘差Rm的標準差σm為17.32×10—3,而去除振動影響后的條紋殘差Rc的標準差σc為7.82×10—3,衰減幅度為54.8%,明顯小于第1 種情況的衰減幅度.

圖7 考慮其他相位噪聲時仿真得到的擬合RMSE 值與(a)延時系數和(b)增益系數的關系Fig.7.The RMSE value of fringe fitting as a function of (a) time delay and (b) proportional element,with other phase noises considered,calculated by simulation.

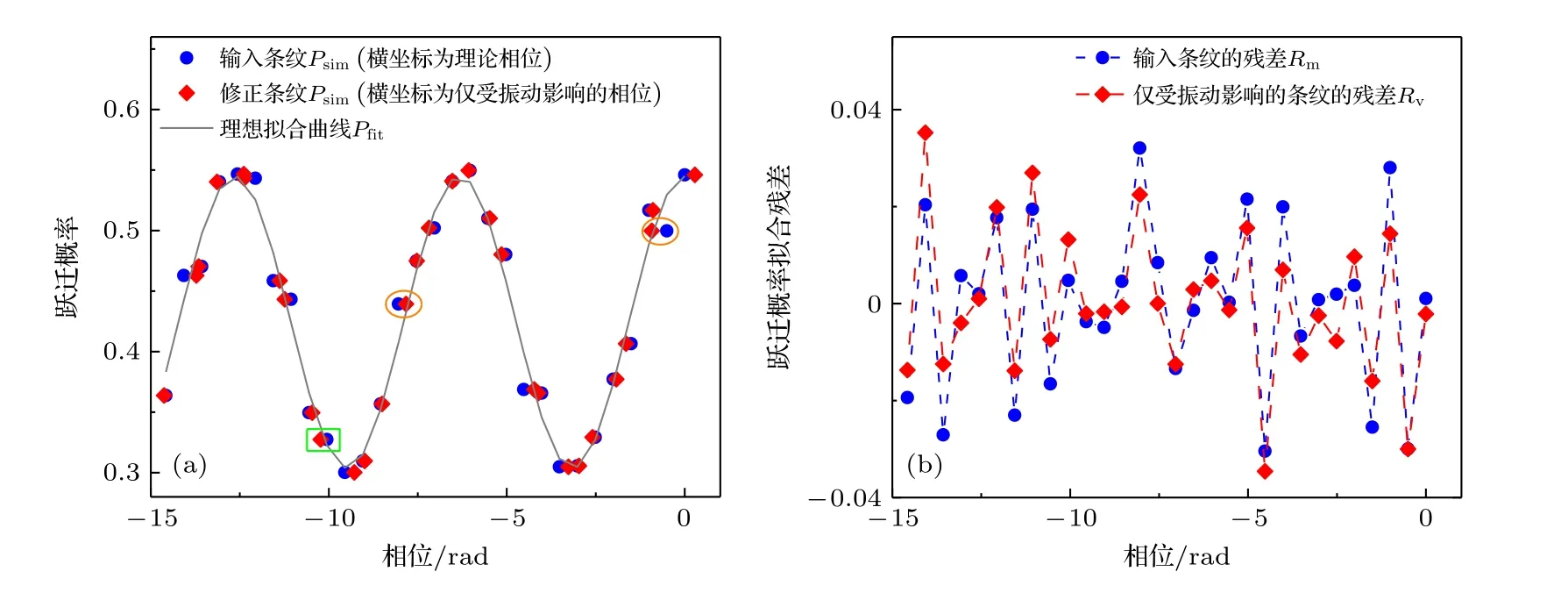
圖8 考慮其他相位噪聲時仿真得到的(a)修正前后的干涉條紋與理論擬合曲線(典型修正點用橘色圓圈和綠色方框標出),(b)原始殘差與計算出的僅由振動導致的條紋殘差Fig.8.(a) The simulated fringe signals before and after vibration correction with the fitted curve as the reference (with the typical corrected data marked by orange circles and green square),and (b) the fitting residual of the simulated fringe signals,with other phase noises considered.

上述結果說明其他相位噪聲將明顯限制振動補償算法的有效性.當振動環境變差,即振動相位Δφvib在總相位噪聲中的權重增加時,算法的有效性將顯著提升.例如,仍取其他相位噪聲Δφothers為±10 mrad 范圍內的隨機值,將參考鏡振動信號vm(t)中隨機振動的幅值Arand增大為原來的10 倍,并記該仿真過程為第3 種情況.此時擬合得到的延時系數為τ=4.1 ms,增益系數為K=0.919,比第2 種情況更接近設定值;原始條紋殘差Rm的標準差σm為29.28×10—3,去除振動影響后的條紋殘差Rc的標準差σc為6.78×10—3,衰減幅度為76.8%,高于第2 種情況.因此,理論上當原子重力儀在復雜振動環境中測量時,該算法將發揮更為明顯的作用.

另一方面,增大數據量可以在小范圍內提升振動補償算法對延時系數和增益系數的計算精度,但對條紋修正效果的提升水平有限.例如,設定其他相位噪聲Δφothers和振動相位Δφvib取值等同于第2 種情況,但將原子團下落的時間間隔減小為1 s.在仿真總時長仍為1 min 的情況下,此時躍遷概率信號的數據量擴大1 倍,達到N=60,記該仿真過程為第4 種情況.此時擬合得到的延時系數為τ=6.8 ms,增益系數為K=0.876,比第2 種情況更接近設定值;但原始條紋殘差Rm的標準差σm為14.80×10—3,去除振動影響后的條紋殘差Rc的標準差σc為6.56×10—3,衰減幅度為55.7%,和第2 種情況差別不大.

表2 匯總了以上所有運算結果.可以看出,補償前后對條紋進行余弦擬合時的RMSE 值的衰減幅度和條紋殘差標準差的衰減幅度及變化規律大致相同.如2.3 節所述,條紋殘差的變化更具有物理意義,因此在后續分析實測結果時不再專門提及RMSE 值的衰減幅度.

表2 仿真運算結果Table 2.Simulated results.

4 實驗結果

4.1 實驗設備

該振動補償算法的實際效果在中國計量科學研究院自主研制的NIM-AGRb-1 型原子重力儀上進行了驗證.NIM-AGRb-1 型重力儀具有兩種工作模式:其一為條紋掃描模式,在此期間拉曼激光波矢keff保持不變,掃頻速率α線性增加,可以得到原子干涉條紋;其二為重力測量模式,在此期間拉曼激光波矢keff不斷反向,即每一次作用于下落原子團時,激光脈沖的波矢keff均與上一次作用時數值相同、方向相反.此時,結合在原子鐘上運用的閉環鎖相技術,可以實現對掃頻速率α的交叉鎖定,進而保證每一次原子團下落后都能得到重力測值g,而不必等待整個干涉條紋測量完畢后擬合出初相位進而計算出重力值,或依據基于不同拉曼間隔T得到的干涉條紋的交叉點位置來計算重力值.配合清華大學研制的被動式零長彈簧結構的隔振系統,該重力儀可實現44 μGal·Hz—1/2的靈敏度,合成不確定度約為5.2 μGal[12].

驗證該振動補償算法時,NIM-AGRb-1 型重力儀在第一種條紋掃描模式下工作,此時重力儀的輸出信號為實測躍遷概率P而非重力測值g,且最多掃描3 個整周期的干涉條紋.本實驗的現場情況如圖9(a)所示,測試地點為中國計量科學研究院昌平院區的重力實驗樓.實驗過程中參考鏡直接放置在重力儀探測腔下方的地面上,旁邊放置英國Guralp 公司生產的CMG-3 ESP 型地震計,其輸出信號的靈敏度為Ks=2000 V·m—1·s[31].探測腔中冷原子團下落期間的激光脈沖的時間間隔為T=80 ms,激光波長約為780 nm,相鄰原子團下落的時間間隔為2 s.受重力儀自身軟件的控制,采集躍遷概率P的數據采集卡的采樣頻率為1 Hz,無法用于對地震計輸出電壓的采樣,因此使用第二臺美國National Instruments 公司生產的PXIe-6361 數據采集卡[32]來記錄地震計的輸出信號Us(t),采樣頻率為500 kS/s,如圖9(b)所示.該采集卡還同步采集了重力儀的某一路觸發信號Utrg(t).重力儀的控制軟件控制采集該信號總比原子團下落時的第1 個π/2 脈沖提前40 ms,從而確保兩臺采集卡分別采樣的數據可以在時間上互相匹配.

圖9 實驗現場圖 (a) NIM-AGRb-1 型原子重力儀;(b)地震計信號及觸發信號采集系統Fig.9.Photograph of (a) NIM-AGRb-1 atomic-interferometry absolute gravimeter,and (b) the data acquisition device recording the voltage signal of seismometer and trigger.

該測試地點位于地廣人稀的郊區,周圍無交通、建筑和大型機械振源,且具有隔振地基,屬于非常安靜的測試環境,其地面振動加速度的功率譜密度如圖10 所示.由于NIM-AGRb-1 型重力儀體積較大,尚無法搬運至其他地點,因此本次實驗暫且僅在該安靜環境中進行.之后該算法的振動補償效果也將在振動條件更為復雜的環境中驗證.

圖10 測試地點的地面振動加速度功率譜密度Fig.10.The power spectrum density of the ground vibration acceleration at the measurement site.

4.2 實驗結果

本次實驗首先采集了10 組數據,每組數據包含30 次原子團下落過程,其他控制參數如前所述.對每組數據分別運行振動補償算法,結果如表3 所示.

表3 10 組數據的實際測量結果Table 3.Measurement results obtained from 10 data sets.

可以看出該振動補償算法在安靜環境中已具有良好的條紋修正效果,去除振動影響后的條紋殘差Rc的標準差σc相比原始條紋殘差Rm的標準差σm的衰減幅度的均值達到44.4%,最大可達58.2%,與表1 中第2 種仿真情況的運算結果基本一致;相比對原始條紋進行余弦擬合時的RMSE值,擬合修正條紋時的RMSE 值也顯著減小.另一方面,各組數據分別計算出的最優增益系數Kopt的標準差為0.115(均值為1.119),計算誤差較小;而最優延時系數τopt的標準差為2.47 ms(均值為3.56 ms),計算誤差較大.前述表2 中第2 種情況的仿真結果已說明,即使Δφothers比Δφvib小1 個量級,τopt的計算誤差也將達到毫秒量級.因此最有可能導致實測結果中τopt的標準差達到毫秒量級的原因仍是其他相位噪聲Δφothers.這再次說明在后續工作中有必要在復雜振動環境中驗證該算法的振動補償效果,即考察振動相位Δφothers在總相位噪聲中所占的權重更大時,σc相比σm的衰減幅度以及延時系數和增益系數的計算精度能否如仿真預測一樣提升.

可以以第1 組數據的計算結果為例觀察振動補償算法的工作過程.如圖11 所示,該算法可以有效搜索出擬合條紋的RMSE 達到最小值時對應的唯一最優延時系數τopt和最優增益系數Kopt.從圖12(a)可以看出,相比原始條紋P(ΔФth),對橫坐標進行振動補償后的修正條紋P(ΔФv)更接近理論條紋Pfit(ΔФth)(典型位置如橘色圓圈所示).補償前對原始條紋P(ΔФth)進行余弦擬合時的RMSE 值為11.2 × 10—3,而補償后對修正條紋Psim(ΔФv)進行余弦擬合時的RMSE 值減小為4.8 × 10—3.原始條紋P相對于理論條紋的殘差Rm(ΔФth)和從地震計實測信號推算出的僅受振動影響時的條紋Pv相對于理論條紋的殘差Rv(ΔФth)也基本吻合,如圖12(b)所示.

圖11 第1 組實測數據的擬合RMSE 值與(a)延時系數和(b)增益系數的關系Fig.11.The RMSE value of fringe fitting as a function of (a) time delay and (b) proportional element,calculated from the 1st dataset of measurement.

圖12 第1 組實測數據(a)修正前后的干涉條紋與理論擬合曲線(典型修正點用橘色圓圈標出),(b)原始殘差與計算出的僅由振動導致的條紋殘差Fig.12.(a) The fringe signals before and after vibration correction with the fitted curve as the reference (with the typical corrected data marked by orange circles),and (b) the fitting residual of the fringe signals,calculated from the 1st dataset of measurement.

實際上還可以采用基于黃金分割原理的二維搜索方法重新編寫振動補償算法流程,以實現對最優延時系數τopt和最優增益系數Kopt的全局搜索.計算結果表明,此時振動補償算法的效果與表3 所示的分別搜索τopt和Kopt時的效果相當.這也再次證明(9)式所示的傳遞函數簡化模型具有合理性.

基于表3 所列的10 組干涉條紋及后續測量得到的50 組干涉條紋進行計算的結果如圖13 所示,其中圖13(a)為這60 組條紋各自修正前的殘差標準差σm以及修正后的殘差標準差σc,圖13(b)為由此得到的σc相對于σm的衰減比.可以看出每組條紋殘差標準差的衰減比的均值仍為45%左右,且分布特征具有隨機性,導致該隨機性分布最可能的原因仍是原始數據中其他相位噪聲造成的隨機干擾.

圖13 修正前后60 組實測干涉條紋的(a)殘差標準差和(b)殘差標準差的衰減比Fig.13.(a) The standard deviations of the fitting residuals of 60 sets of fringe signals with and without the vibration correction,and (b) the reducing factor between them.

如前所述,進行本實驗時NIM-AGRb-1 型重力儀工作在條紋掃描模式,重力儀本身不輸出依據干涉條紋得到的重力測值g.此時,為了分析該振動補償算法對重力測值的影響,可以參考浙江大學提出的方法[19]計算重力測值的離散度:1)對每一組條紋進行余弦擬合時,進一步計算擬合曲線的初相位φinitial(n)(n為條紋序號,n=1,2,···);2)去除φinitial(n)的均值,得到初相位的偏差序列Δφinitial(n);3)根據(4)式,可得重力偏差序列

也就是說,基于修正前后的干涉條紋P(ΔФth)和P(ΔФvib),可以依據(12)式得到振動補償前后的重力偏差序列Δgm(n)和Δgc(n).由于本實驗所在的測量環境無固定振源,僅有與測量過程在時間上不相關的地脈動、輕微的人員走動或實驗樓外的車輛移動等隨機振源,理論上參考鏡振動只影響重力測值的離散度,不會產生恒定的系統誤差.因此補償前后重力偏差序列Δgm(n)和Δgc(n)的對比可以合理地說明該振動補償算法的有效性.

根據上述分析,由修正前后的條紋數據得到的修正前后的重力偏差如圖14 所示.對全部60 組數據,振動補償后重力測值的離散度相比補償前降低了一半左右;由修正前的實測條紋P(ΔФth)得到的重力偏差Δgm的標準差為σgm=51.5 μGal,而由修正后的條紋P(ΔФvib)得到的重力偏差Δgc的標準差σgc=22.0 μGal.σgc相對于σgm的衰減幅度達到57.3%,說明通過該振動補償算法提高干涉條紋的擬合精度可以顯著提升重力測量的精度.

圖14 由60 組實測干涉條紋得到的修正前后的重力偏差Fig.14.The variation of the measured g value deduced from 60 sets of fringe signals with and without the vibration correction.

目前NIM-AGRb-1 型原子重力儀作為計量基準裝置已被設定為長期工作在第二種重力測量模式,即掃頻速率α處于鎖定狀態,無法直接采用本文提出的振動補償算法進行測量.因此本文仍以考察該算法對原子干涉條紋殘差的衰減效果為主.目前實驗室正在研制采用條紋掃描模式來長期工作的可移動式原子重力儀,該振動補償算法也將配合此重力儀在不同的測試環境中進行長期測量,驗證其對包括阿倫方差、重力測量靈敏度在內的關鍵重力參數的提升效果.

5 討論

在前述仿真和實驗過程中,振動補償算法查找最優延時系數時的優化目標是擬合條紋時的RMSE 值,即取RMSE 達到其最小值時對應的延時系數為最優延時系數τopt.另一方面,根據理論分析及圖6(b)、圖8(b)和圖11(b)所示的仿真、實測結果,理論上振動補償效果好時,從地震計信號推算出的僅受振動影響時的條紋相對于理論條紋的殘差Rv(ΔФth)非常接近原始條紋相對于理論條紋的殘差Rm(ΔФth).因此,參考基于相同簡化模型的振動補償方法在光學重力儀中的算法流程[27],實際上還可以嘗試以Rv和Rm的相關系數CR作為優化目標搜索最優延時系數τopt.

相關系數表示2 個列向量之間線性相關的程度,取值范圍為—1 至1,絕對值越大表示相關性越強[33].因此,相關系數CR的絕對值越大,說明Rv(ΔФth)和Rm(ΔФth)越接近,即推算出的振動相位Δφvib越準確,則修正后的條紋越接近擬合曲線,其RMSE值應趨于最小值.需要說明的是,計算相關系數CR時需要對Rc和Rv進行歸一化處理,因此無法以其為優化目標來搜索最優增益系數Kopt.

以CR達到最大值時對應的延時系數為最優延時系數τopt,相應的仿真和實測數據的計算結果分別如表4 和表5 所示.總體而言,采用兩種優化目標時分別計算出的最優延時系數τopt非常接近.如圖15 所示,RMSE 值隨延時系數的變化曲線與相關系數CR隨延時系數的變化曲線具有幾乎完全相同的變化規律,但變化方向相反,符合理論預期.個別情況下采用兩種優化目標時分別計算出的最優延時系數τopt存在毫秒量級的差異,例如表4中第4 種情況和表4 中第2 組數據,其中前者對延時系數的遍歷搜索結果如圖15(d)所示,RMSE 值達到最小值時的延時系數和相關系數CR達到最大值時的延時系數略有區別(分別用黑色和粉色點劃線標出).導致這種情況最可能的原因仍是原始數據中其他相位噪聲造成的隨機干擾.

表4 以相關系數CR 為優化目標時的仿真運算結果Table 4.Simulated results with the correlation value CR as the objective of the algorithm.

圖15 擬合RMSE 值和相關系數CR 與延時系數的關系 (a) 仿真時的第1 種情況;(b) 仿真時的第2 種情況;(c) 實測時的第1 組數據;(d) 仿真時的第4 種情況Fig.15.The RMSE value of fringe fitting and the correlation value CR between the fitting residual of fringes before and after the vibration correction as a function of time delay of (a) 1st simulated dataset,(b) 2nd simulated dataset,(c) 1st measured dataset and(d) 4th simulated dataset.

表5 以相關系數CR 為優化目標時的10 組數據的實際測量結果Table 5.Measurement results obtained from 10 data sets with the correlation value CR as the objective of the algorithm.

對每一組數據,依據振動補償算法計算出最優延時系數τopt和增益系數Kopt后,可以得到最終確定的僅受振動影響時的條紋相對于理論條紋的殘差Rv,進而得到最終確定的相關系數CR.圖16展示了60 組數據中每一組數據的相關系數CR以及修正后的條紋殘差標準差σc相對于修正前的條紋殘差標準差σm的衰減比的對應情況.可以看出,相關系數CR越大,σc相對于σm的衰減比也越大,即振動補償的效果越好.二者的變化趨勢完全吻合,與理論預期相符,再次驗證了該振動補償算法原理的合理性.

圖16 最終確定的Rv 和Rm 的相關系數CR 與修正前后條紋殘差標準差的衰減比Fig.16.The correlation value CR between the fitting residual of fringes before and after the vibration correction,and the corresponding reducing factor of the standard deviation of the fitting residuals of fringe signals after the vibration correction.

還可以直接以2.3 節提出的條紋殘差標準差這一指標作為振動補償的優化目標,即取(11)式所示的標準差σc達到最小值時的延時系數和增益系數為最優值.相應的仿真及實測數據的計算結果表明,在絕大多數情況下以RMSE 值或σc為優化目標時搜索出的τopt和Kopt均完全相同.個別情況下搜索出的延時系數存在毫秒量級的差異,增益系數也可能存在微小差異,如表6 所示.導致這種結果最可能的原因仍是原始數據中其他相位噪聲造成的隨機干擾.

表6 以殘差標準差為優化目標時的仿真及實測數據運算結果Table 6.Simulated and measurement results with the standard deviation of the fitting residuals as the objective of the algorithm.

綜上,當原子重力儀在振動條件更復雜的環境中測量時,即振動相位Δφvib的影響遠大于其他相位噪聲Δφothers的影響時,該振動補償算法的計算

精度和對條紋的修正效果有望得到進一步提升.在后續工作中,該振動補償算法將配合實驗室正在研制的可移動式原子重力儀在復雜環境中進行測試.

總體而言,本文在第2 節定性分析了原子重力儀所用參考鏡與振動傳感器之間的傳遞函數簡化模型中的延時系數τ和增益系數K發生變化的原因,描述了對這兩項系數進行搜索求解的具體振動補償算法流程;在第3 節采用不同的仿真輸入對算法的有效性進行了詳細的定量論證;在第4 節利用重力儀在非常安靜的環境中的實測數據驗證了該算法對原子干涉條紋以及重力測值的補償效果.該算法最大的優點是自適應性較強:相比現有的其他振動補償研究成果,它具有較強的技術意義,可以直接應用于任何能夠掃描出干涉條紋的原子重力儀在任意時間和地點的測量結果,以實現對傳遞函數中的兩項關鍵系數的實時標定,實現當前最好的振動補償效果.另一方面,受限于NIM-AGRb-1型原子重力儀的體積、工作模式和測試任務,該算法的有效性還未能在較為復雜的振動環境中進行驗證;而目前也尚無現有的其他振動補償方法在與本次實驗相同的安靜環境中應用于與該重力儀精度水平相當的原子重力儀上的實驗數據.從該算法與其他振動補償方法在不同測量環境及具有不同噪聲水平的原子重力儀上的實驗結果來看,該算法尚未展現出顯著優于其他方法的補償效果,有待更進一步的測試驗證,其工作原理和具體流程也將在后續工作中不斷優化.

6 結論

應用于原子干涉式絕對重力儀的振動補償方法的主要作用是修正參考鏡振動引入的相位噪聲,從而提高干涉條紋的擬合精度,最終提高重力加速度g的測量精度.現有的振動補償方法在確定的靜態或動態環境中可以實現較高的測量精度,但大部分公開成果沒有介紹對于因測量環境改變而產生的原子重力儀中某些部件的機械傳遞函數的變化進行實時修正的具體應對流程.從長期穩定性的角度來看,這可能在一定程度上限制重力儀在不同環境尤其是復雜振動環境的測量精度.本文介紹了一種應用于原子重力儀的基于搜索傳遞函數簡化模型系數的振動補償方法,著重描述了其具體的算法流程,并利用仿真及實測結果對其合理性和有效性進行了詳細論證.具體而言,該方法將參考鏡的振動信號與測量該振動的傳感器的實際輸出信號之間的真實傳遞函數簡化為一個延時系數和一個增益系數的結合,通過計算軟件對重力儀的干涉條紋和傳感器的輸出信號進行分析,搜索出當前測量環境下這兩個系數的最優估算值,由此可以更加精確地推算出當前環境下參考鏡的真實振動信號.該方法具有自適應性,可以在測量環境改變時對結構的真實傳遞函數進行合理估算,以實現在當時當地對原子干涉條紋最好的修正效果.實測結果表明,在極為安靜的環境中,本文提出的振動補償算法可以將原子重力儀干涉條紋的余弦擬合殘差的標準差大幅衰減,最大衰減幅度達到58%.利用修正后的干涉條紋計算出的重力值的標準差相比修正前衰減57%.根據理論分析和仿真運算,在復雜振動環境中進行重力測量時,該算法將表現出更好的干涉條紋修正效果.因此,該振動補償算法有望直接應用在不同時刻和不同地點對原子重力儀測量結果的實時修正,提高原子重力儀在不同環境尤其是復雜振動環境中的測量精度,其補償效果也將在之后的工作中進行更充分的驗證及優化.