基于OpenFOAM 的磁流體求解器的開發和應用*

李尚卿 王偉民 李玉同4)?

1) (中國科學院物理研究所,北京凝聚態物理國家研究中心,北京 100190)

2) (中國科學院大學物理學院,北京 100049)

3) (中國人民大學物理學系,北京 100872)

4) (松山湖材料實驗室,東莞 523808)

1 引言

激光等離子體與外加磁場相互作用是高能量密度物理的一個重要研究課題.它在磁化慣性聚變[1,2]、實驗室天體物理[3-5]等領域均有應用.人們已經實施了不同構型的外加磁場與激光等離子體相互作用的實驗[6-9],在這些實驗中,采用的激光脈寬一般在1 ns 量級,激光強度約在1014W/cm2量級,產生等離子體的空間尺度約在1 cm 量級,時間尺度約在10 ns 量級.在這些實驗參數條件下,一般用磁流體力學來描述等離子體的演化.目前可以模擬激光等離子體的磁流體力學程序有FLASH[10],GORGON[11],PERSEUS[12]等.隨著研究的深入,設計了更加復雜的磁場-激光等離子體相互作用的實驗構型.實驗設計復雜度的提高主要體現在兩個方面,一是打靶方式變復雜,如Ryutov[13]提出的環形打靶方案;二是磁場構型變復雜,如磁化慣性聚變中的會切磁場構型[14](cusp magnetic configuration).面對這些復雜的設計實驗,需要開發新的模擬程序.本文發展了一款基于流體數值模擬程序OpenFOAM[15]的磁流體求解器.

OpenFOAM 是一個由C++程序編寫的面向對象的開源計算流體力學(computational fluid dynamics,CFD)程序平臺,全稱為Open Source Field Operation and Manipulation.它擁有數十種求解器,可以實現多相流、熱、電磁、化學反應等各種流動的數值模擬.由于OpenFOAM 是開源的,用戶可以根據需求添加物理模型,這為開發磁流體力學求解器提供了便利.不少研究團隊利用OpenFOAM發展了新的求解器來進行磁流體和等離子體模擬的研究,Singh 等[16]開發的不可壓縮磁流體求解器可以模擬液態金屬在管道內的流動;Xisto 等[17]用雙層隱式壓力分離(pressure-implicit with splitting of operators,PISO) 算法,將OpenFOAM 自帶的不可壓縮磁流體求解器拓展到可壓縮流;Ryakhovskiy 等[18]開發了低磁雷諾數條件下的超聲速磁流體求解器;Charles 等[19]開發了Kurganov-Noelle-Petrova格式[20](KNP 格式)和Kurganov-Tadmor格式[21](KT 格式)的理想磁流體黎曼求解器.此外,有研究團隊將OpenFOAM 與傳統的動力學模擬結合起來開展工作,譬如OpenFOAM 與粒子模擬(particle-in-cell,PIC)的結合進行模擬[22].

本文基于OpenFOAM 平臺開發了一種新型磁流體力學求解器MHDFoam,用于求解二維或三維的可壓縮跨音速束流.該求解器將磁場PISO算法植入OpenFOAM 自帶的KT 格式的黎曼求解器rhoCentralFoam,可以控制磁場散度誤差,保證模擬數值精度,避免了非物理現象的出現.MHDFoam 的收斂階在1—2 之間,標準算例的測試結果與FLASH 等程序符合較好.然后,利用開發的求解器計算了激光等離子體分別與外加均勻軸向磁場和電容線圈產生的非均勻磁場相互作用.初步模擬結果表明,在外加均勻軸向磁場條件下,激光等離子體噴流會出現噴嘴和結節,噴嘴位置和結節之間的長度與熱壓比開方成線性關系;在電容線圈產生的非均勻磁場條件下,結節呈非線性分布,而噴嘴的位置受線圈電流參數調控.當線圈中心磁場相同時,小尺寸線圈產生的磁場會加快噴嘴和結節的形成,等效的均勻軸向磁場更大.此模擬結果表明,求解器MHDFoam 的特點是面向工程和實驗,可以做復雜構型下的磁流體模擬.

2 程序開發

2.1 基本方程

從磁流體守恒方程出發,Xisto 等[17]推導出了以流體密度ρ、流體速度U、流體壓強p、磁場B為基本變量的磁流體力學控制方程組:

其中,η為電阻率,ρe為總能量密度.對于采用理想氣體模型的磁流體而言:

方程組(1)即為不考慮黏性、熱傳導等效應的阻抗磁流體方程組,MHDFoam 求解時可以添加這些非線性項.其他磁流體參數如電流密度J,電場E等均可以用基本變量組 (ρ,U,p,B) 結合麥克斯韋方程組、歐姆定律等導出.

2.2 數值算法

基于OpenFOAM 的磁流體力學求解器MHDFoam 的更新算法如圖1 所示.它由兩部分組成:第一部分是OpenFOAM 自帶的中心格式密度基黎曼求解器rhoCentralFoam,可求解可壓縮跨音速氣體;第二部分是一個專用的PISO 算法,用來控制磁場散度誤差.PISO 算法是計算流體力學中的經典算法,其可以求解不可壓縮流體.PISO 算法步驟是先用上一時刻的壓強計算出預測速度,再通過構建壓力泊松方程更新壓強,然后對預測速度進行修正.依此循環若干次,就可以保證場量組(U,p)更新時也滿足?·U ≈0 .Weller 等[15]將PISO算法遷移到不可壓縮磁流體求解器中,可以讓磁場B更新時滿足?·B ≈0 .Xisto 等[17]將PISO 算法拓展到了可壓縮磁流體束流.參考了以上磁場求解方案,開發的MHDFoam 求解器運行過程如下.

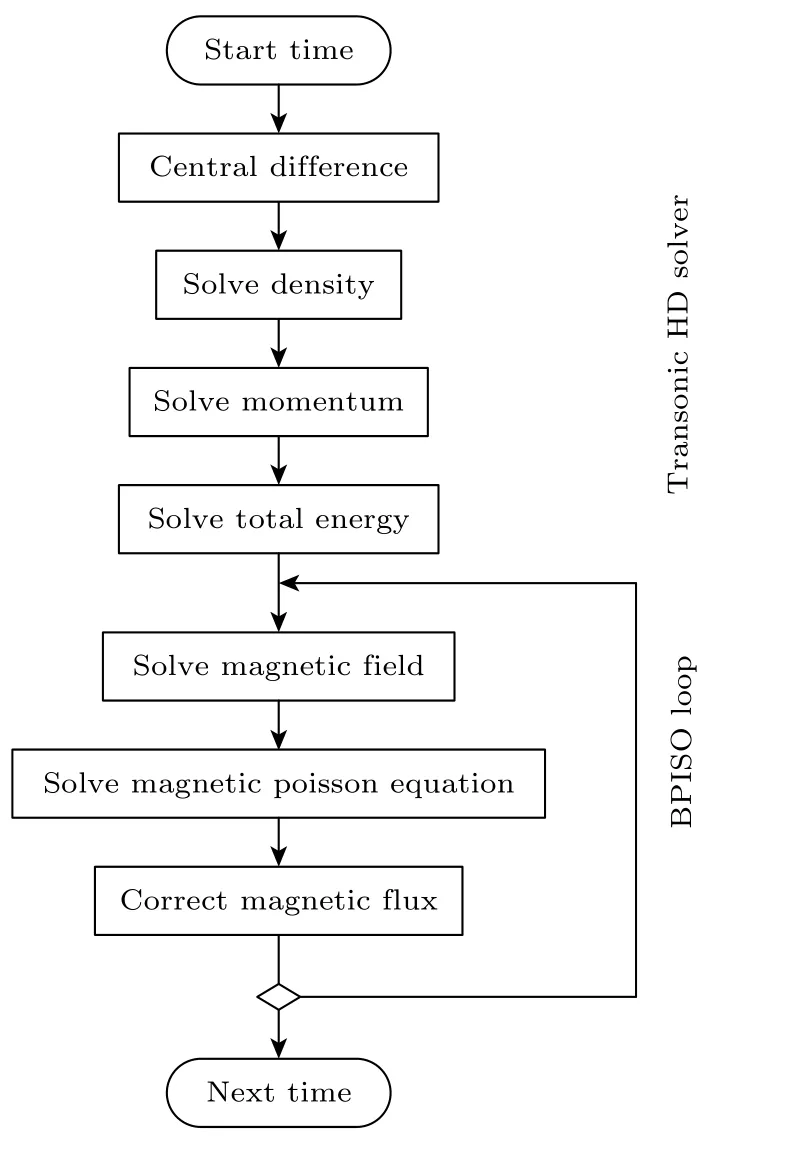
圖1 MHDFoam 求解器的更新算法示意圖Fig.1.Chart flow of update algorithm in the MHDFoam solver.

步驟一求解器首先對密度ρ,動量ρU等流體場量進行KT 格式的高分辨中心差分[21],然后依次求解控制方程組(1)中的密度、動量和能量方程,得到更新后的密度ρ、速度U、壓強p和總能量密度ρe.此階段磁場B作為常量參與計算,沒有更新.

步驟二求解器進入BPISO 循環.首先求解方程組(1)中的磁場演化方程,獲得預測磁場B*.該磁場不滿足無散條件,還需修正.根據電動力學理論,磁場可以寫成B=?×A+??的形式,其中A為矢勢,?為標勢.則可以構造一個虛擬“磁壓”泊松方程?2?=?·B*,解出標勢?.磁場需修正為B=B*-??,再將修正后的磁場代入方程組(1)中的磁場演化方程,得到新的預測磁場B**.依此循環若干次,最終獲得的更新磁場B可以滿足?·B ≈0.該算法本質是Brackbill[23]投影算法.

2.3 程序檢測

為了驗證本文開發的磁流體力學求解器的可靠性,采用了一些標準算例來對數值模擬結果進行了檢驗,檢測結果表明本文發展的程序與這些標準算例結果符合得比較好.本文采用的第一個算例為奧薩格-唐磁流體渦旋(Orszag-Tang MHD vortex)問題[24].其速度和磁場的初始條件為

其中,x,y∈[0 1]2,上下兩邊和左右兩邊采用循環邊界條件.γ=5/3 為絕熱指數.初始速度和磁場的分布如圖2 所示.初始壓強和密度為均勻分布,p0=1/γ,ρ0=1.磁導率μ=1 .以上參數均為無量綱量.圖3(b),(d)分別為t=0.5 時刻的密度和磁場分布.可以看到隨著時間演化,模擬區域出現了許多波交疊的結構,在各個空間尺度下均呈現湍流的特征[25].圖3(a),(c)分別為t=0.5 時y=0.25 處的密度和磁場分布.可以看出本文開發的求解器MHDFoam 與FLASH 程序8wave 求解器[25]和NIRVANA[26]程序的運算結果一致.

圖2 奧薩格-唐磁流體渦旋的(a)初始速度場和(b)初始磁場Fig.2.Initialization of speed field (a) and magnetic field (b)in Orszag-Tang MHD vortex.

圖3 t=0.5 時奧薩格-唐磁流體渦旋的模擬結果 (a),(c) y=0.25 處密度和磁場比較;(b),(d) 密度和磁場廓線Fig.3.Simulation results of Orszag-Tang MHD vortex at t=0.5:(a),(c) 1D cut comparisons of density and B-field at y=0.25;(b),(d) density and B-field contours.

采用相對誤差討論了MHDFoam 求解器的收斂階數.對于t時刻N×N網格奧薩格-唐算例的模擬結果,變量W的相對誤差定義如下[19,27]:

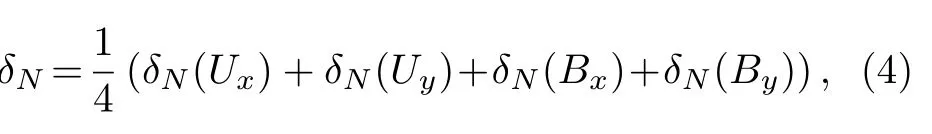
收斂階數的計算公式:

其中為N0粗糙的網格數(N0＜N).模擬結束時的相對誤差和收斂階數分布如表1 所示.可以看到MHDFoam 求解器和KT-MHD 程序的求解器的收斂階數均在1—2 之間.而無磁場情況下的KT格式黎曼求解器的收斂階數為2,這說明收斂階數的降低主要是磁場算法導致的.由于MHDFoam采用了磁場解耦算法,收斂效率比非磁場解耦的KT-MHD 程序的還要稍微低一些.采用這種解耦算法的目的是既能保留中心差分的黎曼求解器,又可以靈活地調整磁場的演化方程(比如考慮雙流體效應時需添加的畢爾曼電勢、霍爾電勢等),這在傳統磁流體黎曼求解器中幾乎無法做到[12].需要注意的是表1 中兩個程序的相對誤差是分別和自身的高分辨網格的模擬結果相比,并不能直接反映和精確結果的誤差.關于該誤差的討論詳見文本的補充材料S1 部分,證明了MHDFoam 求解器的時間穩定性和空間收斂性.

表1 奧薩格-唐問題的相對誤差和收斂階數Table 1.Relative errors (δN) and convergence order (RN) for Orszag-Tang problem.

磁流體轉子(MHD Rotor)[28]是另一個經典二維算例.其模擬空間為x,y∈[-0.5 0.5]2,四邊均為零梯度邊界條件(zero-gradient boundary condition)[26].初始條件為

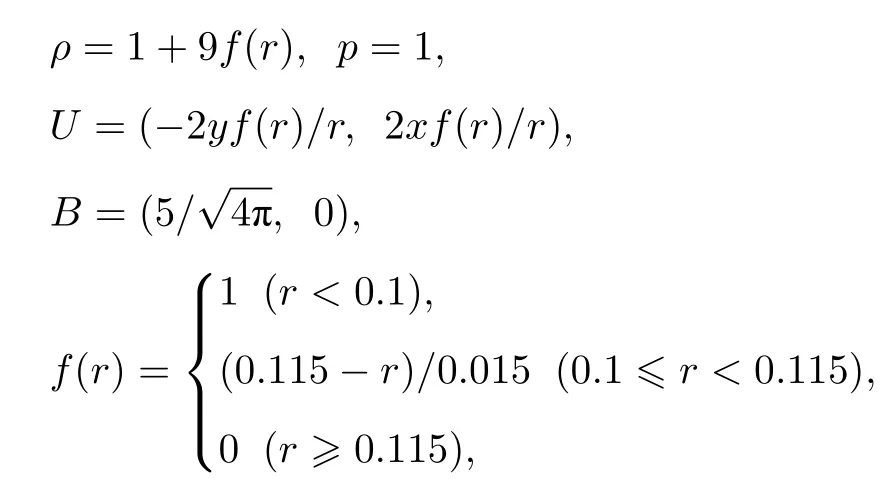
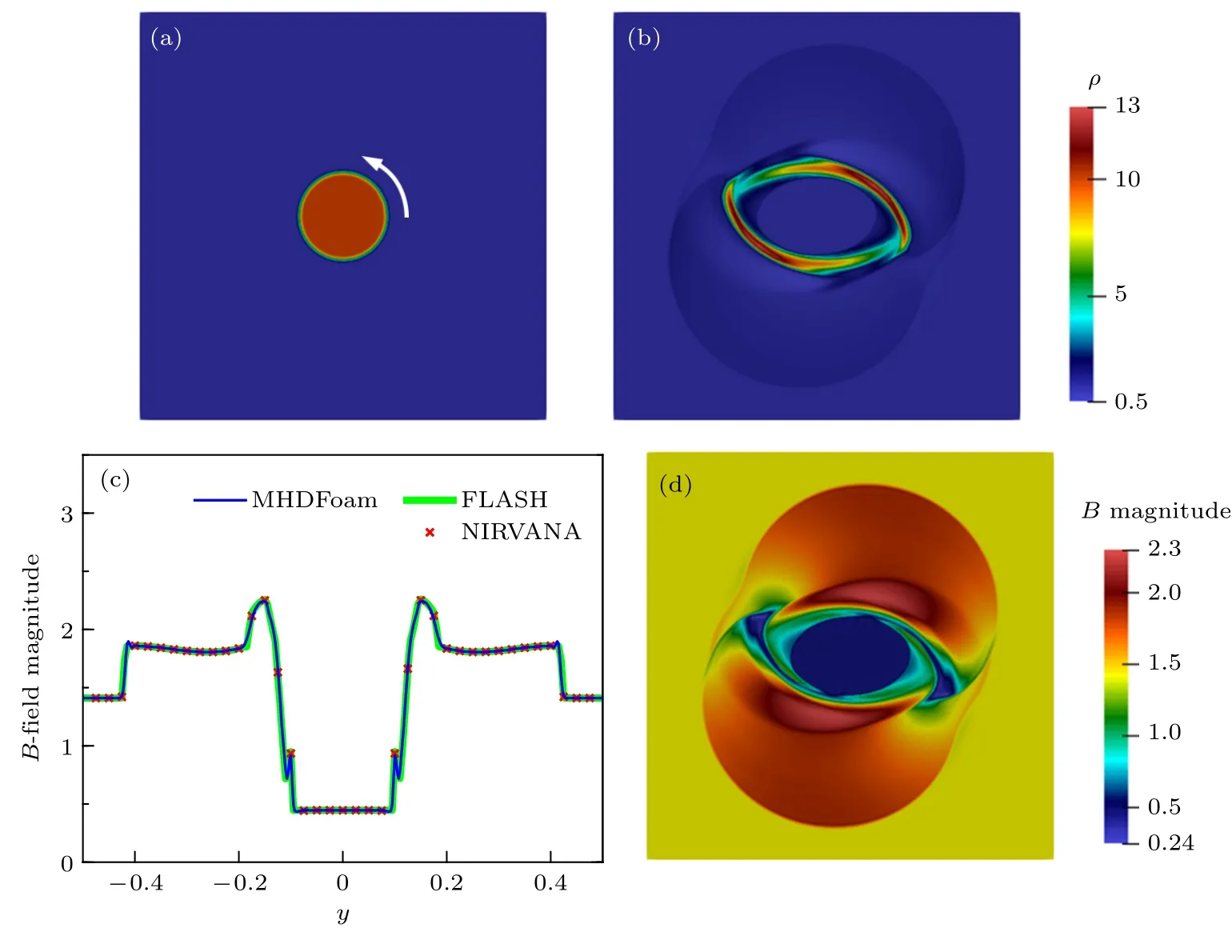
圖4 磁流體轉子 (a) 初始密度廓線;(b),(c) t=0.15 時密度和磁場廓線;(d) t=0.15 時x=0 處磁場比較Fig.4.MHD rotor:(a) Initial density contours;(b),(c) density and magnetic field contours at t=0.15;(c) 1D cut comparisons of B-field at x=0 at t=0.15.

圖5 是磁流體轉子的磁場散度誤差分布.對于600 × 600 網格的模擬結果,磁場的散度誤差約在10—9量級.FLASH 程序采用了6 階自適應網格細分技術,磁場誤差可以達到10—12量級[25].由于在本算例中MHDFoam 并未采用自適應網格細分,本算例中磁場誤差還達不到FLASH 的水平.對于KT-MHD 程序,磁場誤差在間斷面附近達到了約1 量級[19](400×400 網格,奧薩格-唐問題),該現象在圖5 中并未出現.綜合與參考程序FLASH 和KTMHD 的比較,可認為MHDFoam 的磁場誤差控制的精度較高,可以避免非物理數值現象的出現.

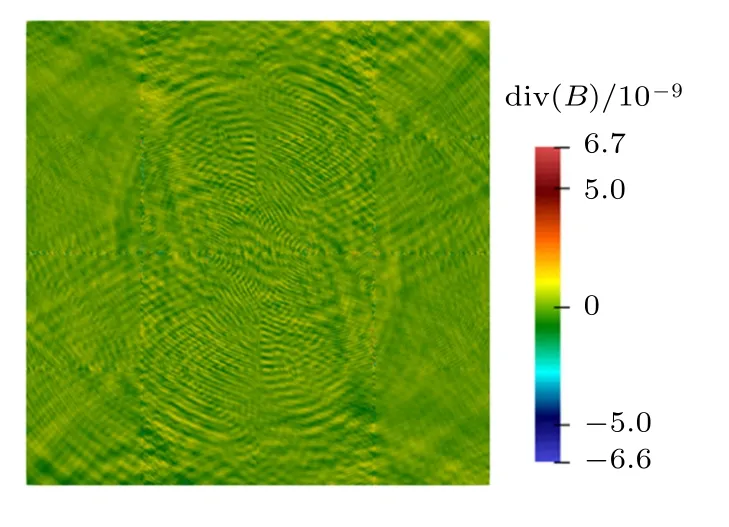
圖5 t=0.15 時MHDFoam 求解磁流體轉子問題的磁場散度誤差Fig.5.Divergence of magnetic fields using the MHDFoam solver at t=0.15 for the MHD rotor problem.

上述兩個算例表明,開發的新型求解器MHDFoam 的測試結果與FLASH 和NIRVANA 等程序的一致.其他標準算例的檢測結果和兼容自適應網格的算例詳見本文的補充材料.

3 應 用

3.1 模擬配置

分別討論均勻軸向磁場和電容線圈產生的非均勻磁場與激光等離子體噴流相互作用的情形.根據文獻[29],當一束能量約為100 J、脈寬為1 ns、焦斑直徑約為200 μm 的激光照射到CH 靶上,產生的激光等離子體的典型速度約為500 km/s,溫度約為106K,壓強約為108—109Pa,密度約為10—4g/cm3.此時輻射致冷效應可以忽略,可以用理想磁流體力學來模擬等離子體的演化.對于軸對稱噴流,二維模擬足夠描述噴流的基本動力學過程[29].因此本文選用計算量比較小的二維模擬作為算例進行分析.

如圖6 所示,模擬空間為一個3 mm × 12 mm的矩形區域.它被劃分為240×960 的網格,網格大小為12.5 μm.以矩形底邊中心為原點,橫向為x軸,縱向為z軸建立坐標系,則有—1.5 mm≤x≤1.5 mm,0≤z≤12 mm.為了更關注激光等離子體的磁流體力學行為,將激光等離子體的產生簡化為一種流體注入的情況.設置入射口處(紅線標注)有密度為1.0 × 10—4g/cm3、溫度為1.6 × 106K、壓強為1.0 ×108Pa、速度為480 km/s 的高溫高密等離子體流入.綠色線處為墻邊界條件,藍線處為無反射邊界條件.模擬空間內存在密度為1.0 ×10—8g/cm3,溫度為300 K 的低密度背景等離子體,它和入射等離子體的質量比為1∶104.磁化背景等離子體的磁場在10—100 T之間變化,注入等離子體在進入磁場之前為非磁化的,入射口處磁場為0.

圖6 二維模擬配置Fig.6.Setup for 2D simulation.

3.2 均勻軸向磁場情形

根據文獻[29],當外加軸向磁場時激光等離子體噴流會出現密度、壓強等參數的周期性增強結構,其中此結構的極大值處稱為結節.圖7 展示了MHDFoam 求解器在圖6 初始配置下的模擬結果.可以看到,當t=22 ns 時,隨著外加磁場的增強,結節的周期長度變短,在模擬區域內出現的次數增加.Lei 等[29]用連續馬赫激波反射原理解釋了結節形成的原因,并指出結節歸一化長度其中L為結節長度/,D為噴流直徑,βnozzle為噴嘴處的熱壓比為流體壓強與磁場壓強比值).本文模擬中也發現了類似現象.圖8(a)中藍色線、紅色線、綠色線分別為圖7 中磁場為40,60,80 T 時的軸線上的密度分布.本文定義原點處熱壓比為βo,噴流上第1 個密度極大值的位置(噴嘴位置)為S,第一個和第二個密度極大(第一個結節位置)之間的距離為L,噴流入口寬度D=1 mm.根據圖8(b),(c),發現它們之間有如下近似關系:

圖7 t=22 ns 時均勻磁場下的密度廓線Fig.7.Density contours at uniform magnetic fields at t=22 ns.

圖 8 (a) t=22 ns 時軸線密度分布;(b),(c)參數L 和S 與關系Fig.8.(a) Density distributions at axis at t=22 ns;(b),(c) parameter L and S as a function of

該結論與文獻[29]中用FLASH 計算的結果類似,這表明求解器MHDFoam 可以模擬外加均勻軸向磁場中的激光等離子體噴流.

3.3 電容線圈產生的磁場情形

2013 年,實驗演示了納秒激光作用電容線圈靶產生了壽命在納秒量級、強度在千特量級的磁場[30],這為激光等離子體實驗中的外加磁場拓展了新的參數范圍.其中此種強磁場由于線圈中形成的電流產生.線圈電流磁場是非均勻的,除線圈平面法向的軸向磁場外,還具有橫向分量,是一種典型的極向磁場.線圈磁場的空間分布依賴于線圈電流I和線圈半徑a,由畢奧-薩伐爾定律可以推導出環形電流磁場的解析分布.為了研究線圈電流參數對等離子體噴流的影響,設計了3 種線圈磁場構型.構型(1):I=0.5 MA,a=3 mm;構型(2):I=0.25 MA,a=3 mm;構型(3):I=0.15 MA,a=1.8 mm.其中構型(2)的磁場分布和磁力線如圖9(a)所示.3 種構型的磁場在x=0 處和z=0 處的分布如圖9(b),(c)所示,其中橙色線代表構型(1),紅色線代表構型(2),黑色線代表構型(3).構型(2)與構型(3)的線圈中心磁場相等(Bo≈52.4 T),但兩者的軸線磁場梯度不同,構型(3)的磁場梯度較大.構型(1)的中心磁場(Bo≈104.7 T)為其他兩個構型的2 倍,磁場大小處處為構型(2)的2 倍.

圖9 線圈電流磁場 (a) xz 平面二維分布;(b) x=0 處分布;(c) z=0 處分布Fig.9.Magnetic field of coil currents:(a) 2D distributions in the xz-plane;(b) 1D cut at x=0;(c) 1D cut at z=0.

本文模擬了線圈電流產生非均勻磁場中的激光等離子體噴流,并與均勻磁場的結果進行了比對.當t=22 ns 時密度廓線的模擬結果如圖10 所示,軸線處的密度分布如圖11(a)所示.可見非均勻外磁場中結節位置分布也是非均勻的.對于z≤5 mm 區域,構型(1)、構型(3)和均勻外加磁場95 T 的噴嘴和結節位置近似重合,這表明在該區域內各構型磁場對噴流的作用效果近似相等.此外,構型(2)的線圈中心磁場Bo與構型(3)的相同,它的噴嘴位置和第一個結節位置卻出現的較晚,作用效果相同的磁場大小約為53 T.

圖11 t=22 ns 時模擬結果 (a)軸線密度分布;(b)無量綱參數S/D 在Ia 相平面上的分布Fig.11.Simulation results at t=22 ns:(a) Density distributions at axis;(b) dimensionless parameter S/D in the Iaplane.

對于非均勻線圈磁場,定義噴嘴位置值相同的均勻磁場為等效作用磁場Be,軸線上噴流密度近似相等的長度為等效作用長度為λe.則圖10 的模擬結果的等效參數可總結到表2 中.

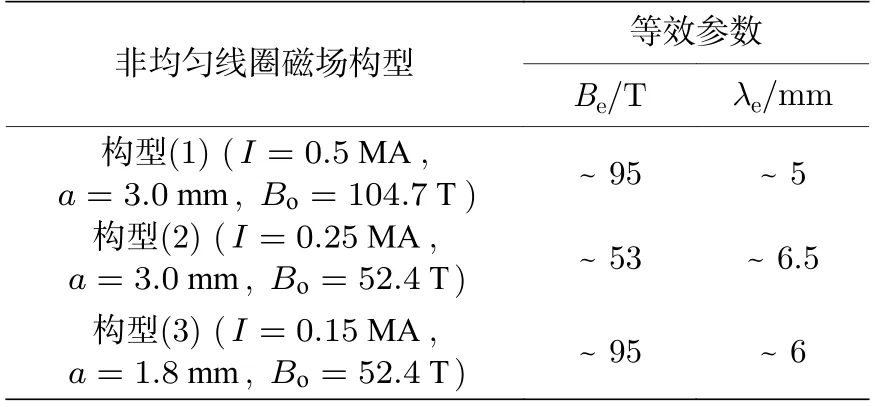
表2 圖10 模擬結果的等效參數Table 2.Equivalent parameters of simulation results in Fig.10.

圖10 t=22 ns 時圖9 配置的非均勻磁場條件下的密度廓線及與均勻磁場的比對Fig.10.Density contours at nonuniform magnetic fields set in Fig.9 at t=22 ns compared with uniform magnetic fields.

考慮到軸線處構型(1)的初始磁場強度至少為構型(3)的2 倍以上,則小于后者的1/2,但在z＜ 5 mm 范圍內兩個磁場對噴流的作用效果近似相等(如圖11(a)中的藍色線和綠色線),這表明(6)式已經不再適用.可認為磁場的不均勻性起到了補償作用.本文在非均勻磁場條件下,擬合出了(6)式的一個較為粗糙的修正關系:

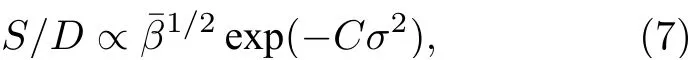
初步的模擬結果表明,電容線圈產生的非均勻磁場在一定空間范圍內對噴流的作用效果可能與均勻磁場的相同.在線圈中心磁場Bo相同時,線圈半徑a越小,磁場不均勻性越大,等效磁場也會變大,噴流和結節出現的越早.對于約100 J 納秒激光等離子體與線圈磁場相互作用的實驗,可以設計參數a/D約為2,Bo約為50 T 的線圈磁場,它在約0.5 cm 空間范圍內對激光等離子體噴流的作用效果與均勻約100 T 軸向磁場的大致相同.這是對文獻[29]中均勻磁場-噴流結節結論的拓展,該初步結論還需進一步的探討和論證.本應用算例同時還證明了MHDFoam 模擬復雜磁場構型下的磁流體問題的能力.

4 結論

為了實現激光等離子體的磁流體數值模擬,我們開發了一套基于OpenFOAM 的磁流體力學求解器MHDFoam.該求解器將一個專用的PISO 算法植入OpenFOAM 自帶的求解器rhoCentralFoam中,用來保證磁場演化的同時較嚴格地滿足磁場無散?·B=0 的約束條件.MHDFoam 的收斂階數在1—2 之間,奧薩格-唐渦旋和磁流體轉子標準算例的運算結果與FLASH 等程序的一致.通過算法測試后,我們用求解器MHDFoam 模擬了外加均勻磁場對激光等離子體噴流的影響,給出了結節周期長度、噴嘴位置與入口熱壓比開方的線性關系.此外,本文還用MHDFoam 模擬了電容線圈產生的非均勻磁場中的激光等離子體噴流,討論了磁場不均勻性對結節和噴嘴位置的影響.初步的模擬結果表明,當線圈中心磁場相同時,小尺寸線圈產生的磁場會加快噴嘴和結節的形成;在厘米空間范圍內對激光等離子體噴流的作用效果與一個較強均勻軸向磁場的大致相同,從而可以替代實驗中一些難以達到的強均勻磁場條件.以上兩個應用算例表明,MHDFoam 可以求解在激光等離子體參數范圍內的、不同磁場構型下的磁流體問題.下一步我們將在這個求解器中添加雙流體和輻射模塊,對激光等離子體實驗進行更精細的模擬.