河南高速公路沿線最大風速精細化預報產品檢驗及訂正研究

肖 瑤 ， 席世平 ， 王 麗

(1.中國氣象局·河南省農業氣象保障與應用技術重點實驗室，鄭州 450003；2.河南省氣象服務中心，鄭州 450003)

引 言

隨著國家經濟與城市化的快速發展，由氣象條件引起的高速公路交通安全保障問題已成為影響生命安全、經濟發展的一個關鍵因素[1-3]。統計結果表明，高速公路交通事故的高發期多為多霧、多雨、多大風、多冰雪和沙塵的季節，高速公路上因惡劣天氣造成的交通事故大約占總事故的30%[4-5]。氣象要素中的大風要素對高速公路交通安全運營有直接不利影響：大風的影響是增加行車阻力、降低能見度，側向大風可能使車輛偏離行車路線，甚至吹翻車輛[6-7]；強風還可能吹倒路邊設施造成交通事故，使交通設施產生振動和變形。2017年中國氣象局公共氣象服務中心研發了一套逐3 h的全國公路交通精細化指導預報。該預報產品可以精細到高速公路沿線每個鄉、鎮，但模式的模擬結果與觀測值之間的誤差不可避免[8-9]，該指導產品的實際預報能力和適用性有待檢驗和分析。

由于初始場的不確定性、大氣的混沌性及模式自身的模擬能力等原因，模式預報產品都存在著不同程度的誤差[10-11]。引入大量歷史資料，發展經驗性方法，建立預報產品與實況觀測的統計關系[12-14]來減小誤差已成為提高數值預報產品準確率的重要方向之一。王彬濱等[15]應用一種諧波分析與人工神經網絡結合的方法，對沿海風塔的數值預報結果進行訂正，訂正后的風速數值預報的系統性偏差明顯下降。曾曉青等[16]將格點觀測融合產品應用于模式預報產品的滾動訂正中，結果表明采用基于模式和實況因子的全格點滑動建模訂正方案具有最佳的訂正效果。近年來，由Cui等[17]提出的卡爾曼濾波類型的自適應遞減平均法在模式誤差訂正[17]中表現良好，已被運用在NCEP全球集合預報系統中。李莉等[18]在對T213全球集合預報系統進行訂正時應用了該方法，有效地改進了2 m氣溫集合預報的均一性及預報的均方根誤差；佟華[19]、肖瑤[20]、邱學興[21]等在應用類卡爾曼濾波方法進行誤差訂正研究時，分別嘗試對該方法進行改進，使模式產品預報質量得到進一步改善。

本文通過對公共氣象服務中心提供的高速公路沿線最大風速精細化預報指導產品進行檢驗分析，然后采用滑動平均法、類卡爾曼濾波遞減平均法兩種方法的多種方案，對該預報指導產品進行偏差訂正，確定最佳訂正方案，得到更適用于行業氣象服務的最大風速精細化預報產品。

1 資料與方法

1.1 使用資料

本文采用的資料是由中國氣象局公共氣象服務中心提供的北京時08時起報逐3 h間隔的高速公路交通最大風速精細化預報指導產品。提取的河南省主要高速公路預報產品，精細到河南省高速公路沿線共511個鄉鎮，空間分辨率為2～3 km。預報資料選取時間長度為2017年12月1日至2018年1月31日，預報時效為24 h。用于對比分析的觀測資料選取CIMISS數據庫中相同時間段的河南省121個國家級自動站的逐3 h最大風速觀測數據。觀測資料經過質量控制，刪除嵩山、雞公山兩個高山站的數據。采用雙線性插值的方法，將高速沿線10 km以內的站點觀測資料插值到指導預報中的鄉(鎮)站的位置上。插值后觀測資料與需要訂正的精細化預報指導產品地理位置一一對應，其數值作為檢驗本文訂正效果的實況分析值。

1.2 使用方法

1.2.1 滑動平均法

通過順序滑動逐期增減數據來計算誤差，計算方法如下：

(1)

其中,t為當前預報時刻，B(t)表示t時刻的偏差訂正值，k為滑動窗長度，i為參與滑動訂正的日期，Vf為預報值，Vo為分析值。

1.2.2 類卡爾曼濾波法

類卡爾曼濾波遞減平均偏差訂正法(以下簡稱遞減平均法)，是通過對不同時段預報偏差的加權平均和迭代更新來估計訂正時刻的遞減平均偏差的。該方法通過增加的資料實時修正預報結果，利用權重平均使計算得到的狀態估計更加接近真實數值，目前已經得到廣泛應用。計算方法如下：

B(t)=(1-w)×B(t-1)+w×(Vf(t)-Vo(t))

(2)

式中，t為當前預報時刻，B(t)表示t時刻的偏差訂正值，B(t-1)表示前一個時刻的偏差訂正值，Vf和Vo分別表示t時刻對應的預報值和真實值，w為遞減平均權重參數，取值范圍為0～1，反映前期不同時刻的偏差值對于預報時刻偏差的貢獻大小。采用“冷啟動”，即t=1時，B(t-1)= 0[22]。

1.2.3 誤差分析方法

本文選用相關系數、絕對誤差、均方根誤差、誤差改進百分比進行檢驗分析。公式如下。

相關系數

(3)

絕對誤差

(4)

均方根誤差

(5)

誤差改進百分比

(6)

其中，Vf和Vo分別表示預報值和真實值,RMSEf和RMSEc分別表示原始預報的均方根誤差和經過訂正之后的均方根誤差。

2 訂正試驗與結果分析

2.1 原始預報誤差特征分析

首先對2017年12月1日至2018年1月31日最大風速精細化預報指導產品和實況分析值進行對比檢驗，分析指導產品的預報性能。圖1是2017年12月1日至2018年1月31日高速公路沿線各站點平均最大風速實況與原始預報值對比圖(以3 h預報時效為例)。經過檢驗，原始預報場與實況場分布形態相似，長濟高速、連霍高速洛陽段、寧洛高速平頂山段、二廣高速濟源段、京港澳高速鶴壁段及濟廣高速實況場平均最大風速的幾處大值區，滬陜高速等實況場平均最大風速的幾處小值區，在預報場中均有反映。但與此同時也可以看出，原始預報產品較實況值呈現出明顯的系統性偏差，預報結果相比實況值大體呈現較為一致的偏低現象，且在各預報時效上均有體現。

對原始預報指導產品3-24 h預報時效的絕對誤差、均方根誤差進行檢驗分析(圖2)發現：絕對誤差和均方根誤差的時間變化趨勢較為一致，其中夜間的預報誤差小于白天的，且夜間誤差變化相對平緩；計算的3-24 h的平均絕對誤差為1.19 m/s，均方根誤差為1.54 m/s。該產品在精細化行業氣象服務中具有一定的應用價值，尚需要通過有效的訂正方法對不同預報時效的預報指導產品進行偏差訂正。

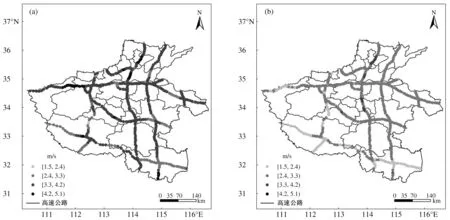
圖1 2017年12月1日至2018年1月31日3 h預報時效的平均最大風速實況(a)與原始預報(b)空間分布

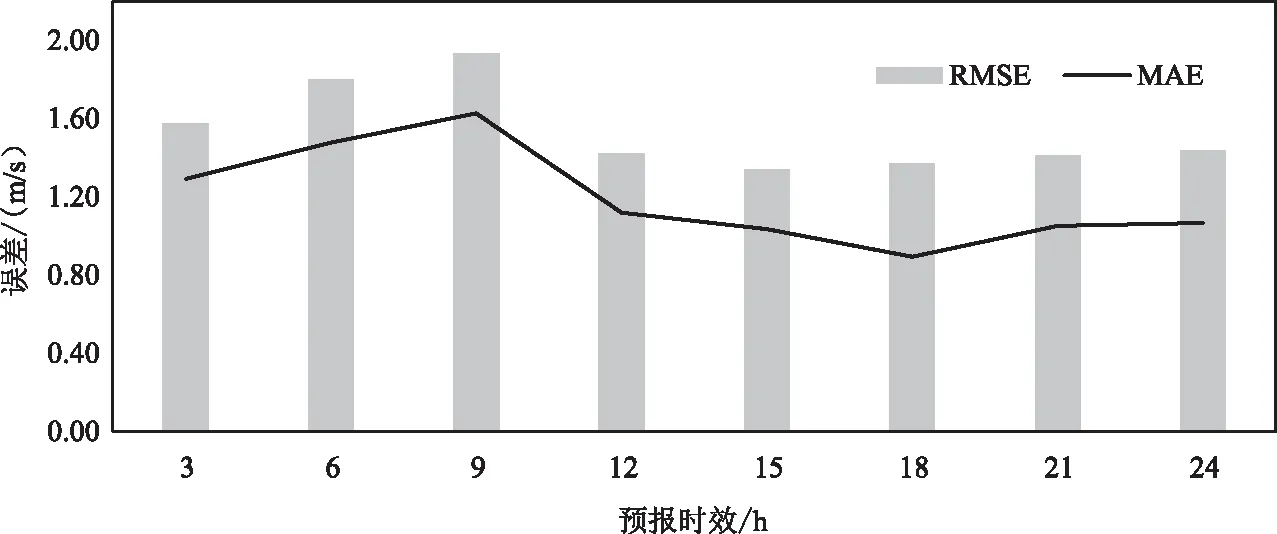
圖2 2017年12月1日至2018年1月31日最大風速原始預報絕對誤差、均方根誤差隨預報時效的變化

2.2 滑動平均誤差訂正效果檢驗

針對上述河南高速公路交通最大風速精細化預報指導產品,應用滑動平均方法進行訂正試驗。結合自然天氣周期、雙周期振蕩，滑動窗長度分別選擇5 d、7 d、14 d 3種方案進行滑動平均訂正。

原始預報均方根誤差的地理分布如圖3(a)所示(以3 h預報時效為例)，均方根誤差范圍為0.9～3.1 m/s，整體來看豫東南的均方根誤差小于豫西北的，均方根誤差的大值區域主要在長濟高速、連霍高速三門峽-洛陽段、滬陜高速南陽段、京港澳高速黃河以北段等，部分路段均方根誤差超過2.5 m/s。訂正前均方根誤差與經過3種滑動平均方案訂正后均方根誤差的差值如圖3(b)-(d)。總體來看，滑動平均法呈現“+”的訂正效果，大部分站點均方根誤差減小幅度為0～0.8 m/s，減小的大值區域主要在西部，像連霍高速三門峽-洛陽段、滬陜高速南陽段等較好地對應了原始預報的誤差大值區域。結合均方根誤差隨預報時效的變化(圖4)來看，3種滑動平均訂正方案中5 d和14 d滑動平均方案訂正效果較好，尤其是在原始預報不夠理想的3-9 h預報，訂正后均方根誤差最大減小了0.23～0.65 m/s，減小幅度更為明顯。

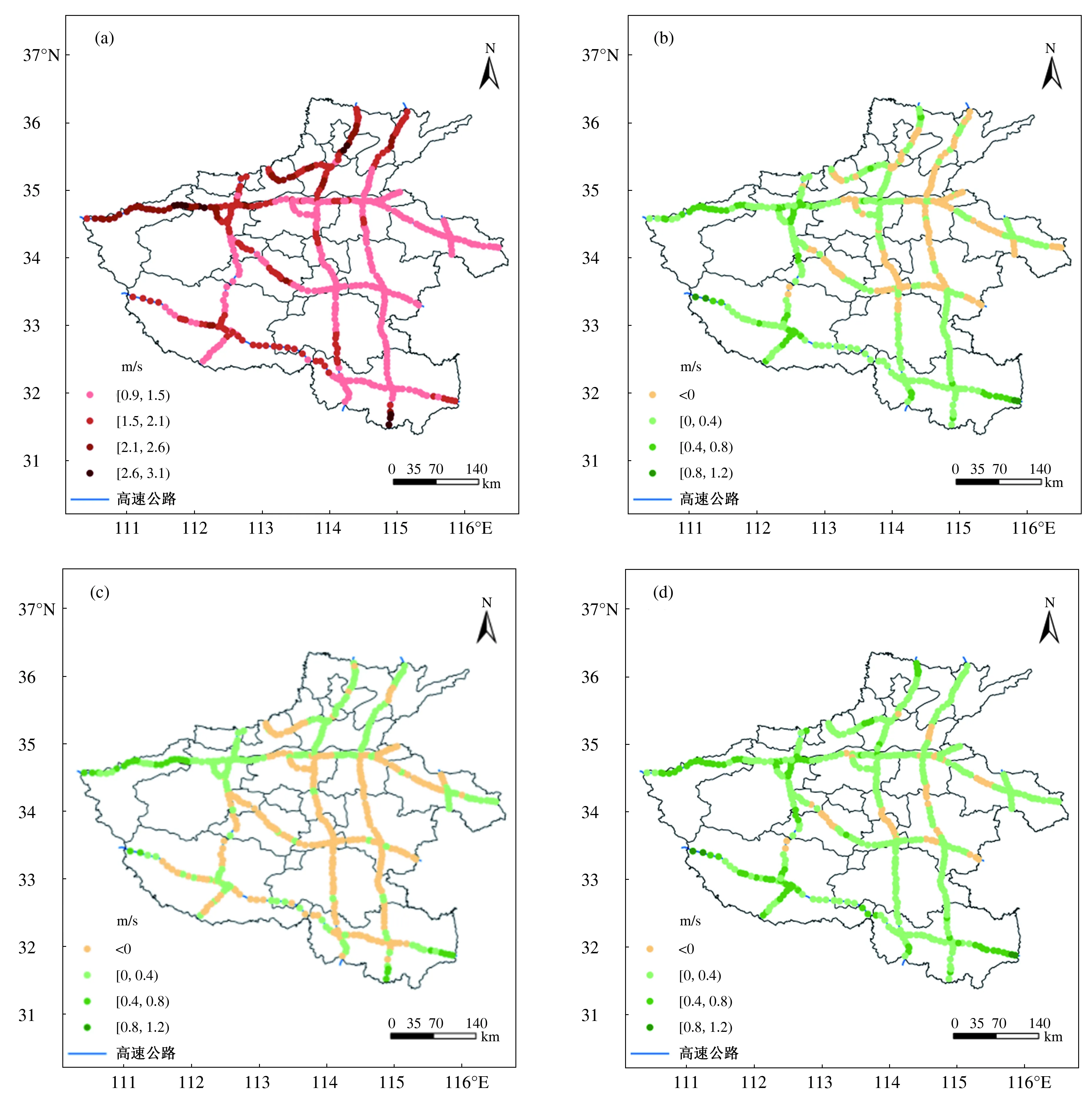
圖3 2017年12月1日至2018年1月31日3 h預報時效的最大風速原始預報均方根誤差(a)及其與

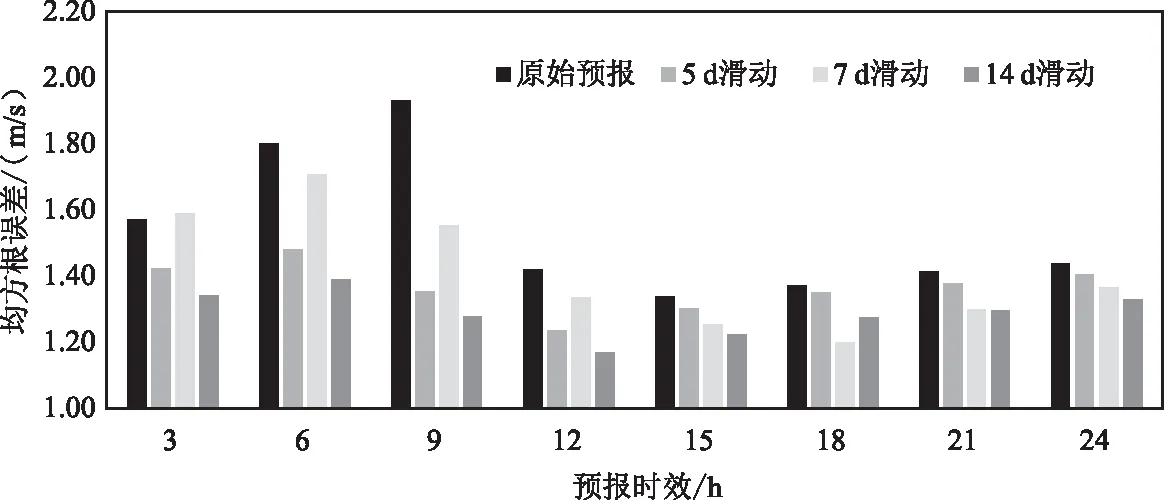
圖4 2017年12月1日至2018年1月31日最大風速原始預報及滑動平均訂正后的均方根誤差隨預報時效的變化

表1為經過滑動平均法訂正后的誤差檢驗分析。由表1可以看出，經過訂正后3-24 h預報時效的平均絕對誤差和平均均方根誤差均顯著減小，3種方案中14 d滑動平均訂正法的效果最優，與實況場的相關系數提升了0.02，平均絕對誤差減小了0.22 m/s，平均均方根誤差減小了0.25 m/s，誤差縮小15.08%，且在各個預報時效上均有體現。

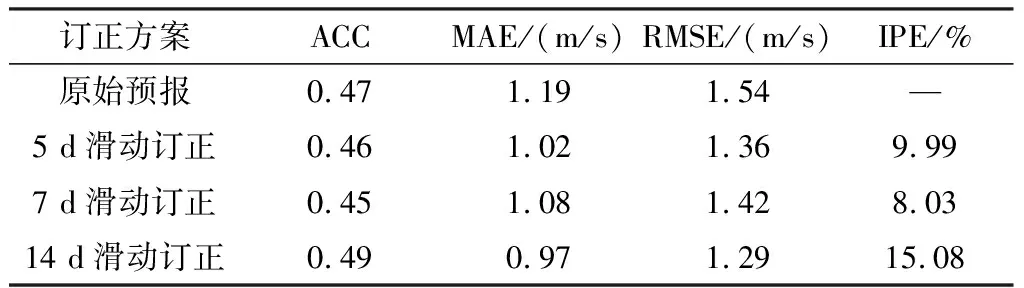
表1 2017年12月1日至2018年1月31日最大風速原始預報及滑動平均訂正后的誤差檢驗

2.3 遞減平均誤差訂正效果檢驗

針對上述河南高速公路交通最大風速精細化預報指導產品，應用遞減平均方法進行訂正試驗。在應用遞減平均法時，參數w的選取，首先參考NCEP的取值,為固定的常值權重0.02。經檢驗發現，w為0.02時訂正效果不理想。對參數w進行敏感性試驗發現，針對河南地區最大風速訂正時，參數w取0.05時訂正后的預報結果較為理想，下文簡稱w(常數)遞減平均方案。進一步從w的物理意義出發，參考佟華等[19]的改進思路，考慮到選取不同長度的歷史資料信息對訂正結果的影響不同及各站地形、海拔等地理條件的不同，將參數w改進為包含地理信息的函數。w的取值范圍在0到1之間，以0.001為間隔，對前15 d的滯后平均進行訓練，以模式預報的系統誤差達到收斂且每個站點的預報偏差最小為標準確定權重系數w(i)，其中i為涵蓋地形、海拔等因素的站點信息，下文簡稱w(i)遞減平均方案。

經過2種遞減平均方案訂正后的均方根誤差較訂正前的均方根誤差減小的差值分布如圖5所示(以預報時效3 h為例)。總體來看，遞減平均法呈現“+”的訂正效果。高速沿線絕大部分站點的均方根誤差明顯減小，其中減小的大值區域主要位于西部、東南部，像連霍高速三門峽-洛陽段、滬陜高速南陽段等較好地對應了原始預報的誤差大值區域，一定程度上改進了原始預報“地理不均衡”的問題，即誤差越大的地方改進效果越明顯。圖6為經過遞減平均訂正后均方根誤差隨預報時效的變化。由圖6可看出，經過遞減平均法訂正后，均方根誤差在各個時效上均明顯減小，其中在原始預報誤差偏大的3-9 h均方根誤差減小幅度更為顯著，即對于白天的訂正效果好于對夜里的訂正效果，訂正后的預報效果在各個時效上更為平均。結合表2的誤差檢驗分析，可以看出，經過訂正后3-24 h預報時效的平均絕對誤差和平均均方根誤差均顯著減小，其中改進的w(i)遞減平均法訂正的效果更為明顯，與實況場的相關系數提升了0.04，平均絕對誤差減小了0.25 m/s，平均均方根誤差減小了0.28 m/s，誤差改進百分比為17.23%，訂正效果較為理想。

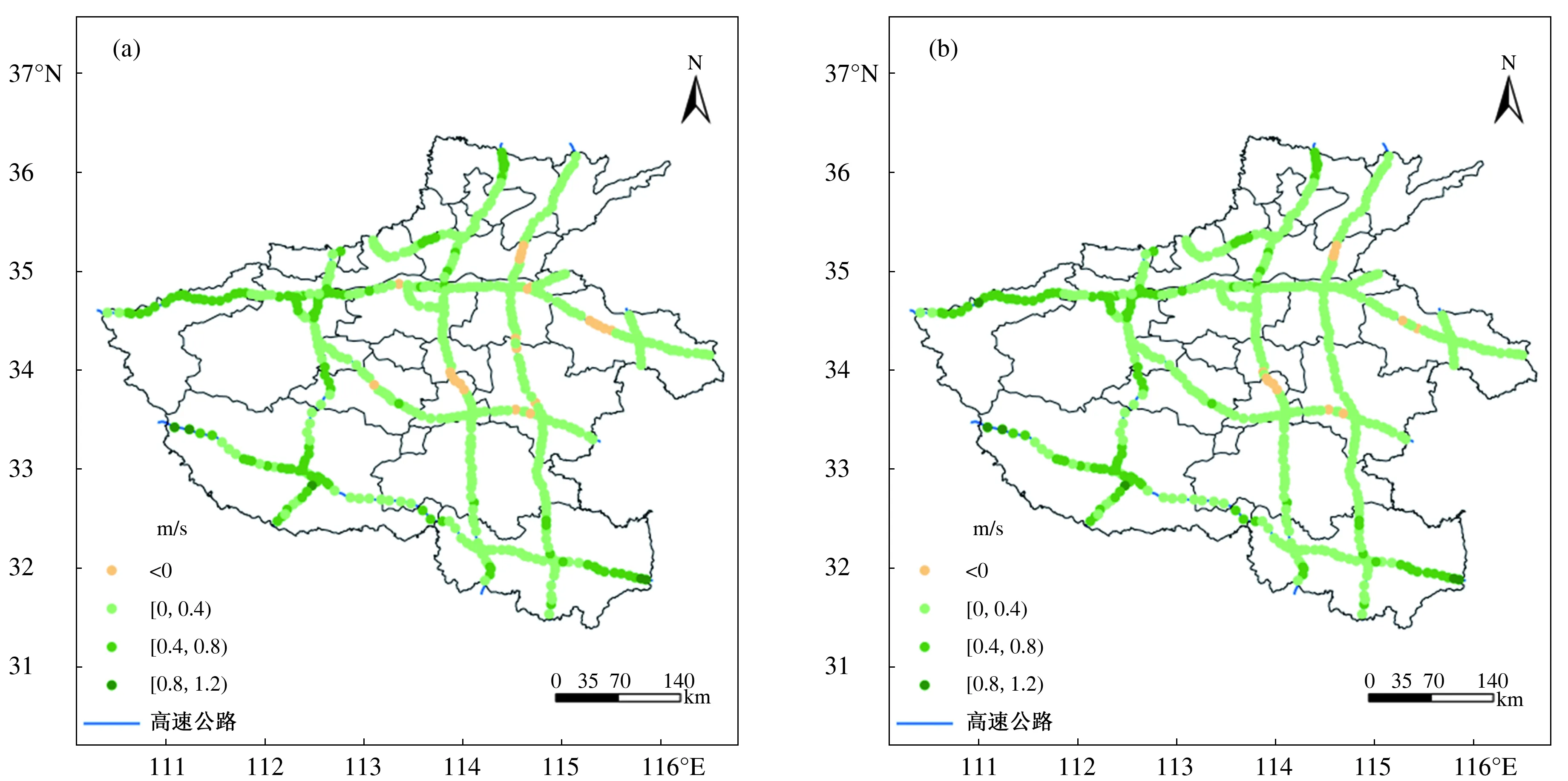
圖5 2017年12月1日至2018年1月31日3 h預報時效的最大風速原始預報均方根誤差與w(常數)遞減平均(a)、

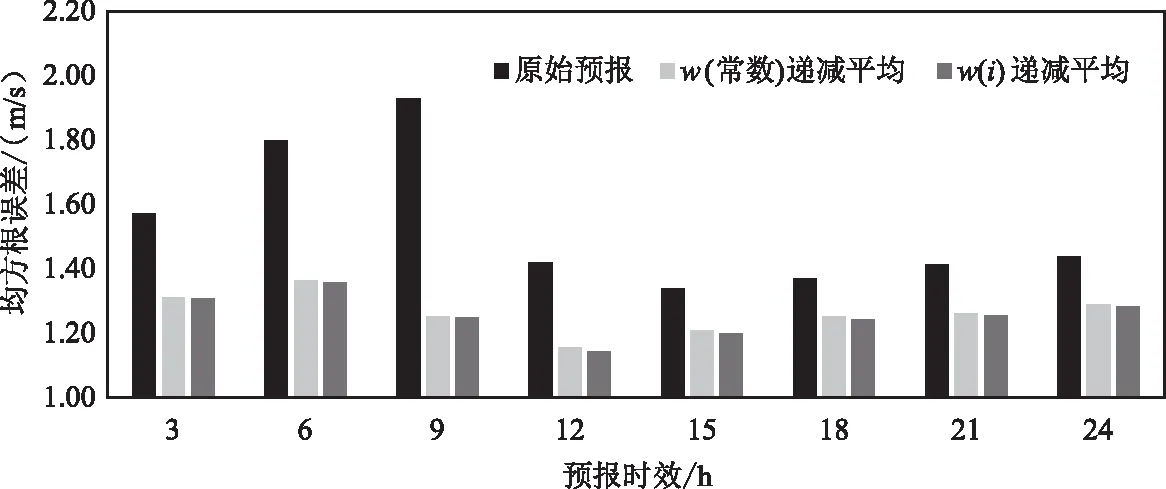
圖6 2017年12月1日至2018年1月31日最大風速原始預報及遞減平均訂正后的均方根誤差隨預報時效的變化

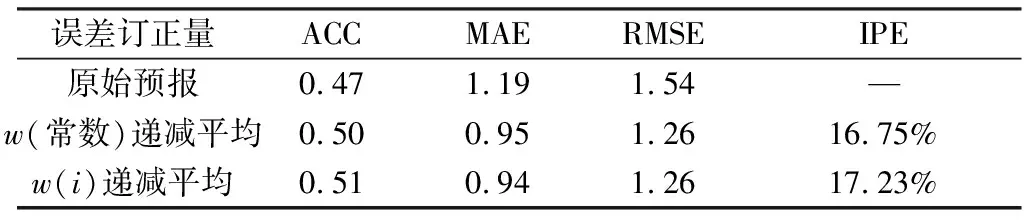
表2 2017年12月1日至2018年1月31日最大風速原始預報及遞減平均訂正后的誤差檢驗

綜合來看，兩種訂正方法均表現出較好的訂正能力，在原始預報誤差較大的站點和誤差較大的預報時效，訂正效果更為明顯。兩種方法中遞減平均方法的訂正效果整體上好于滑動平均法的。其中選擇14 d滑動窗長度是當前最優的滑動平均方案；改進的w(i)遞減平均方案優于w(常數)遞減平均方案，且是當前幾種方案中訂正效果最好的。

2.4 不同風速等級的誤差訂正分析

以原始預報結果和訂正方案中表現最優的w(i)遞減平均法訂正結果為例，分析不同等級風速情況下的訂正效果(圖7)。按照實況風速大小進行分級統計，風速間隔取為1 m/s。總體來看，隨著實況風速的增加，原始預報及w(i)遞減平均法訂正預報的均方根誤差都呈現先減小后增大的趨勢。實況風速為0-4 m/s，預報均方根誤差隨著風速的增加而減小；當風速大于4 m/s時，預報均方根誤差隨著風速的增加而明顯增大；經過訂正后的預報結果在風速為3-5 m/s時預報誤差最小。從w(i)遞減平均法的訂正效果來看，風速在0～2 m/s內訂正表現為“-”的訂正效果，即對于微小風速，訂正方案并不理想；當風速大于2 m/s時均表現為“+”的訂正效果，當風速大于6 m/s時，雖然原始預報誤差增大，但w(i)遞減平均法訂正效果仍然較為顯著；尤其是在風速大于8 m/s范圍時,訂正能力表現最優，預報均方根誤差平均減小了0.87 m/s，平均誤差縮小達20%。

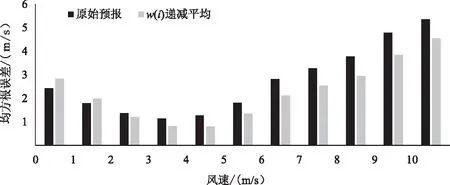
圖7 2017年12月1日至2018年1月31日不同等級風速訂正前后的均方根誤差

3 結 論

(1)對中國氣象局公共氣象服務中心提供的2017年12月1日至2018年1月31日河南高速公路沿線最大風速精細化指導預報進行檢驗分析發現，預報產品表現出有較好的預報能力，但仍存在較明顯的系統性偏差。

(2)采用滑動平均、類卡爾曼濾波法遞減平均訂正法進行誤差訂正研究，訂正結果表明，兩種訂正方法均表現為正的訂正效果，較好地降低了模式預報結果的系統性偏差。在原始預報誤差較大的站點和誤差較大的預報時效，兩種方法的訂正效果更為明顯。滑動平均法訂正后24 h平均均方根誤差由原始的1.54 m/s減小到1.29～1.42 m/s，遞減平均法訂正后平均均方根誤差進一步降低到1.26 m/s，誤差縮小8.03%～17.23%。其中選擇14 d滑動窗長度是當前最優的滑動平均方案；改進的w(i)遞減平均方案優于w(常數)遞減平均方案，且是當前幾種方案中訂正效果最好的。

(3)不同等級的實況風速其誤差訂正結果存在差異。以w(i)遞減平均訂正法為例，風速在0～2 m/s范圍內,表現為負的訂正效果，當風速大于2 m/s時均表現為正的訂正效果。當風速大于6 m/s時，雖然原始預報誤差增大，但w(i)遞減平均法訂正效果仍然較為顯著；當風速大于8 m/s時,訂正后的預報均方根誤差平均減小了0.87 m/s，誤差縮小達20%。