公司特征是否和收益率成非線性關系？

魏杰　文欣玥

摘? ?要：資產定價領域已成為金融學研究的熱點。與傳統因子模型不同，本文提出了加權非線性因子模型，將公司特征的未知函數作為因子載荷，時變的因子收益作為權重，研究股票超額收益率與公司特征之間是否存在非線性關系，以及模型對我國股票市場的適用性和解釋力度。選取1995年7月—2020年6月我國A股上市公司的財務數據，考慮公司規模特征、價值特征和動量特征，采用核函數回歸方法同時估計出因子載荷和因子收益，結果發現三個特征都是顯著的，并且動量特征與收益率成非線性關系。此外，與美國股票市場相比，本文模型更加適用于中國股票市場，解釋力度更強;與Fama-French三因子模型相比，本文估計誤差更小。本文提出的模型在基本面分析和因子投資策略領域中具有借鑒意義。

關鍵詞：股票市場;加權非線性因子模型;非參估計;資產定價

中圖分類號：F830.91? 文獻標識碼：B? 文章編號：1674-2265（2022）05-0080-09

DOI：10.19647/j.cnki.37-1462/f.2022.05.011

一、引言

在我國金融市場中，股票超額收益率的決定因素一直是資產定價領域研究的熱點。最為大眾所接受的是Fama和French（1993）[1]提出的三因子模型（以下簡稱FF三因子模型），他們通過構建投資組合研究了公司特征與橫截面收益率之間的線性關系，而本文利用非參數估計方法，將公司特征的函數作為因子載荷進行估計，研究公司特征與股票收益率之間的非線性關系。目前，國內文獻鮮少運用非參數估計方法，資產定價方向的研究主要分為兩類：第一類是通過增加新的因子，構建投資組合，研究流動性風險、投資者情緒、公司治理、全要素生產率對收益率的影響（宋光輝等，2017;齊岳等，2020;張少華和陳慧玲，2021;李雙琦等，2021;周學偉等，2020）[2-6];第二類是采用機器學習方法研究多因子選股對交易策略的影響（干偉明，2018;周亮，2021）[7，8]。

資產定價模型的解釋力度在不同國家存在差異，田利輝和王冠英（2014）[9]發現我國和美國金融市場的定價因子具有較大差異。Connor等（2012）[10]提出非參因子模型同時估計公司特征函數和因子收益，這種模型在中國股市的適用性也有待驗證。

本文以1995年7月—2020年6月的中國股市收益率月度數據為樣本，根據公司市值和賬面市值比特征構建資產定價模型，其中，將公司特征形成的未知函數作為因子模型中的因子載荷，采用非參估計核函數回歸方法，同時估計出特征函數和因子收益，回歸結果顯著，證明了股票收益率和公司特征之間確實存在非線性關系。此外，本文還和美國股市進行對比，實證結果發現本文構建的模型對中國股市的解釋力度更大、誤差更小。本文提出的模型適用于公司特征數較多、無法構建投資組合及高維面板數據的情況。

本文的主要貢獻在于：第一，研究范圍更廣。傳統因子模型采用排序方式進行分組，只研究了變量間的線性關系。而本文提出的加權非線性因子模型包括傳統因子模型的研究范圍，把因子載荷看作公司特征的未知函數，函數形式可以是任意的。第二，更符合實際情況。傳統因子模型假設因子載荷是已知的，在組內是不變的，根據因子載荷估計因子收益。而本文模型中因子載荷是未知的，也需要估計。第三，本文模型可以解決維度詛咒問題，當傳統因子模型出現高維數據時，由于構建投資組合個數有限，過高的維度會導致參數無法估計。本文通過對高維數據進行迭代估計，從而實現降維，可以研究連續變量。第四，本文對傳統的三因子模型進行深入探討，豐富了我國股票超額收益和公司特征存在非線性關系方面的研究。由于我國金融市場還不是有效市場，本文研究發現公司特征對超額收益有非線性影響，可以為基本面分析中國股市的超額收益提供依據。此外，最近較流行的多因子投資策略也是通過分析各種因子實現套利，所以本文提出的因子模型可以作為參考。

二、文獻綜述

古今中外，關于資產定價模型理論研究的文獻非常多，從單因子模型發展到八因子模型。Sharpe（1964）[11]、Lintner（1965a;1965b）[12，13]等提出的模型是最早的單因子模型，用以研究資產收益率和市場系統性風險的關系。但是他們沒有考慮規模效應和價值效應。于是，Fama和French（1993）[1]提出FF三因子模型，研究市場、規模、價值因子對股票超額收益率的影響。后來，學者們又引入動量因子（Carhart，1997）[14]、流動性因子（Pastor和Stambaugh，2003）[15]構建四因子模型，而Novy-Marx（2013）[16]把四因子模型中的規模因子換成盈利因子進行研究。Fama和 French（2015;2016）[17，18]在FF三因子模型基礎上引入公司的盈利和投資因子，發現價值因子是“冗余”變量。Hou等（2015a;2015b）[19，20]則提出新的考慮規模、投資、盈利因子的資產定價模型。六因子和八因子模型也相繼被提出，發現模型可以提高解釋力（Barillas和Shanken，2018; Sko?ir和Loncarski，2018）[21，22]。最近幾年，用資產定價模型來研究我國股票市場的文獻也逐漸增加，主要集中在資產定價模型對比、模型的實證檢驗以及多因子選股策略等領域。趙勝民等（2016）[23]發現FF三因子模型比五因子模型更適合我國股市。李志冰等（2017）[24]檢驗了Fama-French五因子模型在我國股權分置改革前后的因子顯著性。Liu等（2019）[25]提出了適合中國的價值因子、規模因子來解釋股市的異象，如用凈利潤與市價比代替賬面市值比。但他們都只研究了因子和超額收益率的線性關系，沒有擴展到一般情況，未關注公司特征的函數與收益率之間的非線性關系。

國外學者認為因子和資產回報率之間可能存在非線性的關系，于是提出了非線性因子模型。Connor和Linton（2007）[26]改進因子模型的估計方法，把公司特征的函數作為因子載荷，進行非參核回歸，同時估計特征函數和因子收益，以核函數為權重，通過格點將規模特征和價值特征對應在一定區間內，構建模仿FF三因子的投資組合，證明了因子收益的估計量比其更有效。但是這種構建投資組合的方法只考慮了離散變量的情況，不能解決因子面臨的維度詛咒問題。他們進一步完善估計方法，放松限制，考慮在高維面板數據下，在連續變量存在時變情況下同時估計因子收益和因子特征函數（Connor和Linton，2012）[10]。這種非參估計方法比線性回歸和構建組合方法的適用范圍更廣，不用構建投資組合，不用考慮因子個數，適用所有情況，還能解決維度詛咒問題。

近年來，國外學者深入研究基于公司特征的因子模型，發現公司特征對超額收益率影響很大。Freyberger等（2020）[27]利用LASSO方法篩選出公司特征，用非參估計方法研究這些特征如何影響預期收益，提供增量信息，從而提高預測精度。Raponi等（2020）[28]研究估計預期收益時貝塔資產定價模型的有效性，假設特征和因子載荷在不同資產間具有完全異質性而且允許在橫截面上是任意相關的，發現公司特征的解釋力比因子載荷更強。

通過文獻回顧發現，國外文獻較多采用非參估計方法進行研究，而國內文獻以傳統資產定價模型的實證檢驗和策略應用為主，形成了豐富的研究成果。但是，很少有學者將國內外研究結合起來，考慮股票收益率和公司特征之間存在非線性關系，將非參估計方法應用到我國股市的資產定價模型上。因此，在我國快速發展的金融市場中，研究非線性因子模型的解釋力度具有一定的理論和現實意義。

三、模型構建

（一）模型設定

傳統的資產定價模型采用的貝塔因子模型如下：

其中，[Rit]是個股[i]在時間[t]上的超額收益率，[αi]是截距，代表非系統風險為0時的資產收益率，[βiK]是第[i]個資產第[K]個因子的因子載荷，[fKt]是第[K]個因子在時間[t]的收益。

假設因子數據集與股票收益率之間存在非線性關系，即因子數據集形成的未知函數和股票收益率存在線性關系。所以，本文構建基于公司特征的因子模型來刻畫股票市場的非線性現象。

其中，[rit]是第[i]個股票第[t]期的收益率;[rf]是無風險收益率;[fut]和[fjt]是因子收益;[Xij]是可觀測的股票特征，假設不會隨時間變化;[gjXij]是基于股票特征的未知函數，不會隨時間變化，是模型估計的非參部分;[εit]是均值為0的股票收益率。因子特征函數[gjXij]可以把特征[Xij]映射到因子收益，所以因子收益[fjt]和因子特征函數[gjXij]相關。

我們可以看到，公式（2）是一種將基于特征的函數加權求和的一元因子模型，其中權重是因子收益[fjt]，會隨時間變化，是時變參數。市場因子[fut]反映了和公司特征無關的資產共同收益的部分，所有資產的市場因子都有單位貝塔。它反映了所有股票共同移動的趨勢，屬于面板數據模型的共同因素。

（二）特征函數識別條件的提出

我們假設觀測的特征都是獨立同分布的，據此提出識別限制：對于每一個特征，特征函數橫截面平均值為0，特征函數橫截面的方差為1，即[E*gjXji=0，var*gjXji=1]。其中，[E*]是某個分布[P*]的期望，即[E*gj=gjxdP*jx]。選擇不同的分布函數會影響特征的解釋，[var*gjXij=1]這一條件設置了因子收益的大小，[E*gjXij=0]這一條件會影響對截距的解釋。如果我們使用總體分布，則[E*gjXij=0]表示截距可以被解釋為平均資產的收益;如果我們使用流通價值加權的總體分布，則[E*gjXij=0]表示截距是流通價值加權平均資產的收益。為了簡化我們的理論，本文使用不加權總體分布。

四、方法對比

（一）構建投資組合回歸法

我們先來回顧一下FF三因子模型方法。首先，把所有股票按照流通市值從小到大的順序排列，前50%作為小市值（S）組，后50%作為大市值（B）組;用同樣的方法，把所有股票按賬面市值比分為三組，排名前30%的是低賬面市值比（L）組，后30%的是高賬面市值比（H）組，中間40%的是中間（M）組;從而構建SH、SM、SL、BH、BM、BL六大類投資組合，計算出規模因子（SMB）和價值因子（HML），而市場因子是市場所有股票的加權收益率與一個月國債收益率的差。其次，分別基于市值和賬面市值比的大小將所有股票等分為五組，構建出25個投資組合，以流通市值作為權重，計算出加權的組合收益率。最后，以組合的超額收益率作為被解釋變量，對市場因子、規模因子和價值因子進行最小二乘時間序列回歸。

雖然通過構造投資組合方法可以解釋哪些因素影響股票收益率，但是FF三因子模型還存在三點缺陷：第一，當因子個數較少時，可以通過有限的分類形成投資組合，但是當存在大量因子時，該方法不再可靠，無法通過構造多個投資組合來實現估計，這也正是本文需要解決的問題。第二，在估計因子載荷時，該模型沒有考慮到動量因子等其他特征因子，誤差項中可能存在和股票收益率相關性較高但未被解釋的因子，可能會出現測量誤差問題。第三，因子載荷的估計是在已知因子收益的前提下進行的，但是在現實中，因子收益和因子載荷都存在未知的可能性，需要同時估計出來。

（二）網格點估計法

Connor等（2007）[26]提出了新的構建組合方法迭。他們的模型采用格點法，每個數據對應一個目標特征向量的網格點。和FF三因子模型相比，他們計算投資組合收益率時采用核函數加權方法而不是流通市值加權平均法，并且根據每個資產的特征向量和目標向量的距離確定核函數的權重。

假設[J]個特征有[M]個不同的目標值，定義隨機向量[X]集合中的元素[xmj]成為選中的值，所以目標特征向量的格點有[H=MJ]種組合，定義所有的目標向量組成的集合為[xh=xh1，xh2，…，xhJ′，h=1，2，…，H]，在給定[h]對應的向量[（m1，m2，…，mJ）]，每一個[xh]是[J]向量的目標特征值。從公司[i]中觀察的特征值放入[Xi=Xi1，Xi2，…，XiJ′，i=1，2，…，n]。

其中，[rht]是加權投資組合收益率，[rit]是第[i]個股票第[t]期的收益率，[rht]是條件期望[rit]在[Ci=ch]下的非參估計量，[ωhi]是采用高斯核函數構建的核函數權重。

根據（5）式，構建基于核函數的投資組合收益如下：

對于每一個格點[xhj]，都有對應估計的因子特征值，由于[gj0=0]，[gj1=1]，所以[g1j=0]，[g2j=1]，他們對[M-2J]個因子特征函數g（.）和[J+1T]個因子收益進行估計，定義[θ=M-2J+J+1T]列向量參數矩陣，將公式（6）改寫成非線性形式，得到：

其中，[δhj，m]是虛擬變量，當組合[h]有目標值[xmj]時，它就是1，否則就是0。

其中，加權矩陣[V]是對稱正定矩陣，可以從數據中估計出來。[Qnθ]是四次多項式，有唯一合適的緊集。他們采用迭代加權最小二乘方法找到最小值[θ=gT，fTT]，使它滿足：

Connor等（2007）[26]提出的估計方法可以同時估計因子特征函數和因子收益，得到的估計量是一致的且更有效。但是，此方法的缺點在于太過于依賴多元核函數方法創造投資組合，當遇到高維數據時，這些多元核函數會嚴重限制因子的個數，所以因子個數較多時，該方法變得不可靠。而本文提出的方法不需要多元核函數就可以進行估計。

（三）加權非線性因子模型非參估計

上述兩個估計方法要求構建多個投資組合和多元核函數，估計的特征數目有限，而本文提出了一種新的估計策略，能快速估計出因子收益和因子特征函數，并且適用于多特征的情況。在非參估計部分，我們把問題分解成單獨估計每個特征的子問題，子問題之間不斷地迭代，最終得到估計結果，這是加權非參回歸方法中的標準技巧。

我們先建立總體最小二乘標準：

只要滿足上文提到的兩個識別條件，就可以找到最小化的[QTf，g]了。

由于本文模型中[f]和[g]未知，都需要估計出來，而且最小化問題沒有唯一解而是一組向量空間，所以我們采用無約束變量[gjxj]來替代[gjxj]。

其中，[P*jxj]是特征[j]的概率分布函數。

由于真實期望值無法得到，所以我們采用有界可調整的核函數回歸估計量。我們估計條件期望[Eyit|Xij=x]如下：

比如，[Khx，y=Kxhx-y=h-1Kxh-1x，y]表示[x]在[Xij]內部支持。[K]是核函數，[h]是帶寬。我們假設每個協變量在已知區間[[x，x]]里，協變量密度是非0有界的。我們需要對核函數做出有界調整確保誤差在每個地方都是相同大小的。

當資產總體是固定的時候，最小化問題可以看作一系列線性回歸問題，采用最小二乘法估計系數。但是當資產總體是隨機的時候，我們先固定因子特征函數[g.]，分別對（11）式中的[fut]和[fjt]求一階導，得到：

接著，我們再固定因子收益[fut]和[fjt]，采用Gateaux對（11）式在[ψ.]函數方向上求點導數。

我們通過不斷迭代解決這一問題，共分為四步：

第一步是設置第一次迭代的初始值[f0]和[g0]，滿足一致性;第二步是按照（18）式，根據[f0]估計第二次迭代的[g1]：

五、實證研究

（一）數據來源及說明

本文從國泰安數據庫中選取了中國A股市場所有股票的個股收益率和公司財務報表等信息，研究區間是1995年7月—2020年6月，總共有300個月，樣本量為382884。。因為A股市場于1995年才開始逐漸發展壯大，之前上市公司數量不夠多，信息不夠齊全，而且每年末的公司財務報表會在下一年的7月份之前全部披露完成，所以選擇1995年7月作為樣本區間起點。我們把1995年7月—1996年6月的數據看作1995年的年度數據，以此類推。對數據進行篩選和預處理，剔除掉流通市值排名后10%的公司。為了防止出現借殼上市的公司，不考慮上市時間小于6個月的公司、金融行業公司和ST股票。以流通市值加權平均法計算的考慮現金紅利再投資的綜合A股市場回報率作為市場收益率，以月度化定期整存整取一年的利率作為無風險利率，以考慮現金紅利再投資的月度個股回報率作為股票收益率。使用市值賬面比（流通市值與所有者權益的比值）作為價值特征，個股超額收益率是個股回報率減去無風險收益率，市場因子收益是市場收益率減去無風險收益率。為了方便研究，以上數據統一轉化成月度數據。

以往文獻研究發現，規模效應、價值效應、動量效應對股票橫截面收益有重大影響。因此，構建基于公司規模、價值、動量特征的非線性因子模型：

其中，[rit]是個股收益率，[rf]是無風險收益率，市場因子[fut]反映了和公司特征無關的資產共同收益的一部分，G（.）表示基于公司特征的特征函數，[Size]是流通市值，[Value]是市值與賬面價值的比，[Mom]是個股的前12個月收益率之和，[fit]代表因子收益。

（二）評價模型解釋力度

本文評價模型解釋力度的指標共有兩個，分別是根均方誤差（[RMSE]）和平均去中心化的[R2]統計量（[UR2]）。[RMSE]值越小，[UR2]值越大，則代表模型的解釋力度越強。

其中，[yit]是真實的個股超額收益率，[yit]是模型估計出的擬合值。

（三）描述性統計

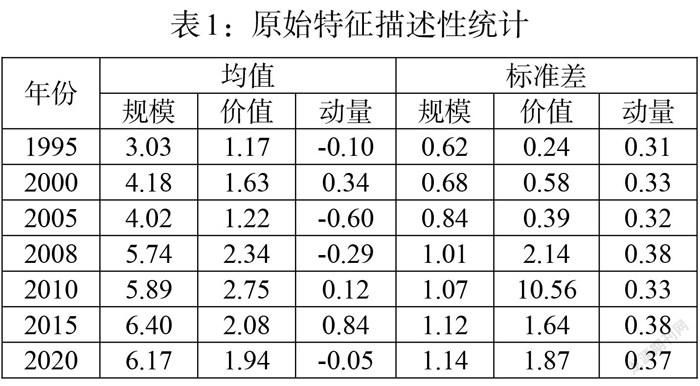
本文對原始三個特征進行描述性統計（見表1）。由于篇幅限制，只列舉每隔5年以及中間年的6月份的均值和標準差。結果發現，規模特征的均值最大，動量特征的標準差最小。

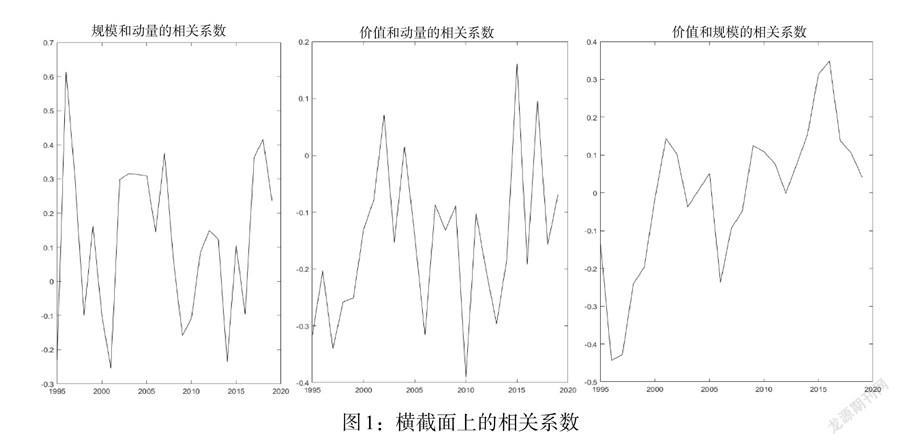
把每年的7月作為橫截面，將3個公司特征兩兩匹配得到3組橫截面之間的相關系數（見圖1）。從圖中可以看出，這3個特征之間的相關性都是從負數到正數持續震蕩。平均來說，動量特征和規模特征成正相關，動量特征和價值特征成負相關，價值特征和規模特征成正相關。

六、模型效果

（一）估計結果

當解釋變量是時變的，直接估計特征函數是不可行的。我們將因子載荷的估計集中在-3和3之間的61個等距網格點上，相鄰網格點間隔0.1，使用線性插值法計算因子載荷，再根據資產收益率和因子載荷估計因子收益。由于因子載荷和格點是線性關系，這個過程可以提高算法速度。

選擇高斯核進行非參估計條件期望，這種核的優點在于能夠平滑地估計連續變量。設置格點的帶寬等于樣本密度的10%分位數，這就暗示了90%的觀測值不在格點內。當帶寬越窄時，數據更密集一些，反之，數據更稀疏一些。

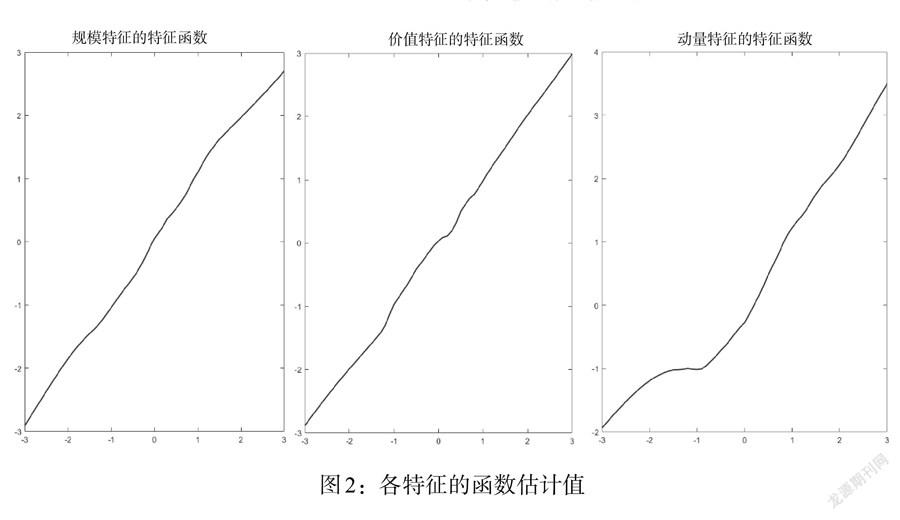
將估計出來的因子載荷進行標準化（見圖2）。從圖2可以看出，這3個特征函數都是單調遞增的，規模特征、價值特征的函數接近于線性，而動量特征的曲線是非線性的。

（二）模型解釋力度

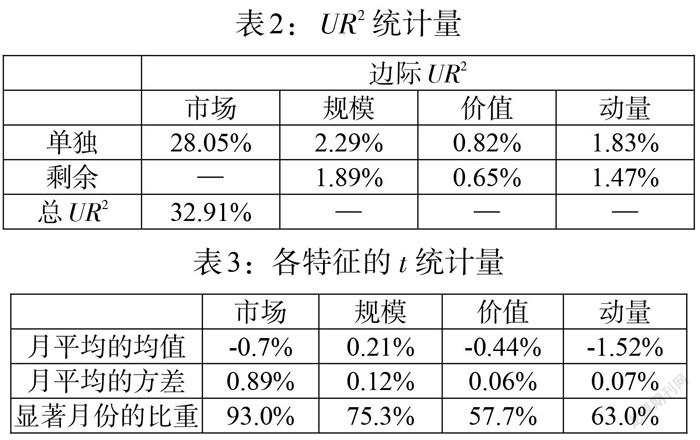
在每一步迭代估計中，因子收益是前一個迭代因子特征函數的回歸系數。為了衡量因子解釋力，我們采用最后一步的特征函數估計值，并且對所有特征、單個特征、剩余特征進行橫截面回歸（見表2）。表2中第一行是只對當前的特征進行回歸得到的[UR2]，第二行是剩余特征的[UR2]，最后一行是三個特征非線性回歸得到的[UR2]。從表2中可以看到，市場因素在解釋力上是主要的，其次是規模特征、動量特征和價值特征。

為了和Connor（2012）[10]研究美國股票市場的[UR2]進行對比，選擇1995—2007年的中國股票市場作為觀測區間，計算出[UR2]為35.97%，比美國股市[UR2]19.81%要大一些，說明本文提出的模型解釋力度更強，更適用我國的股票市場。

我們通過計算橫截面上估計系數的[t]統計量檢驗每個特征的顯著性（見表3），發現在95%置信水平上，每個特征的顯著月份的比重都超過50%，說明所有特征是顯著的。

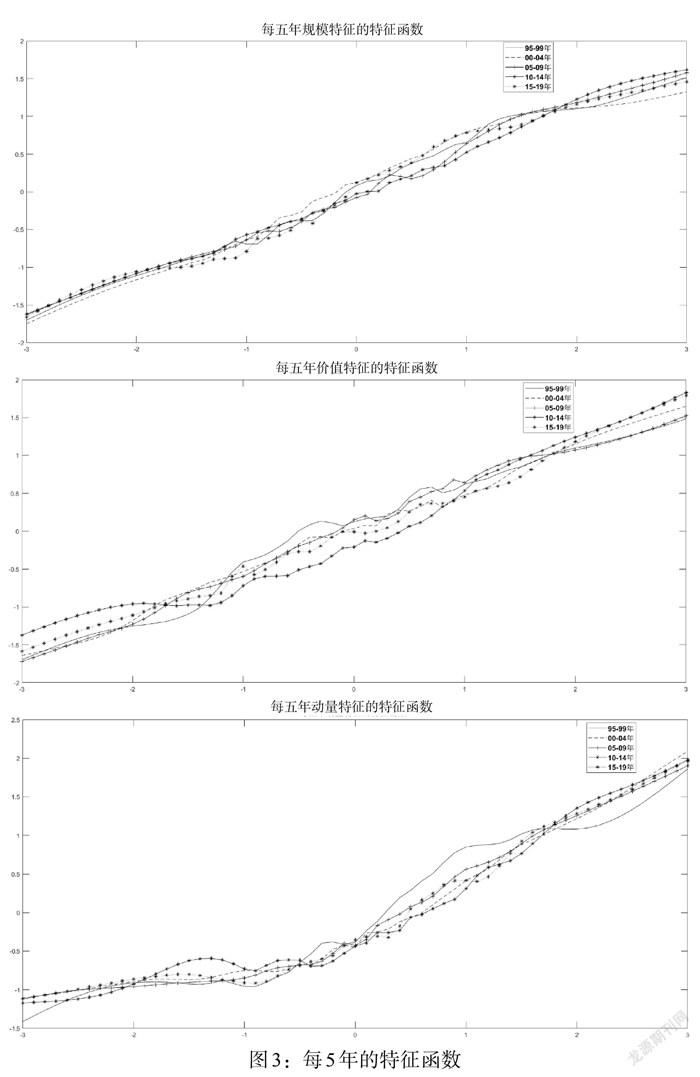
將25年數據拆分為5個5年估計區間，分別估計特征函數，并且進行標準化，如圖3所示。結果發現這三個特征的每五年特征函數相差不是很大，大體保持在一條線上。說明本文估計的特征函數具有穩健性。

（三）與FF三因子模型對比

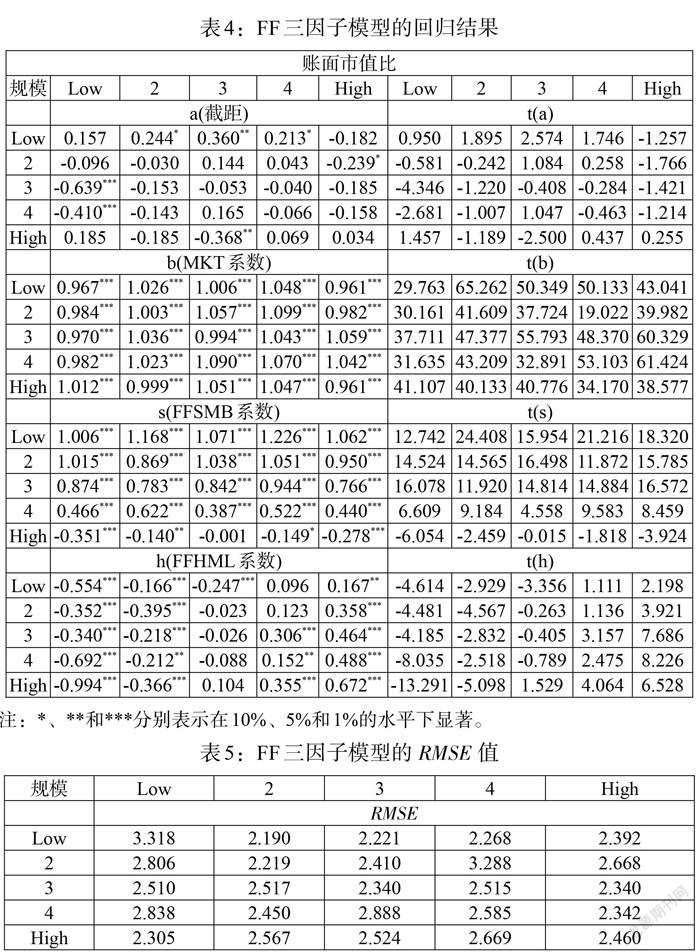
本文按照FF三因子模型，構建25個投資組合的加權平均收益率，計算規模因子和價值因子，進行回歸（見表4）。結果發現所有投資組合中市場因子均顯著，而在有些投資組合中規模因子和價值因子不顯著。但是，本文構建的非線性因子模型中市場、規模和價值三個特征都顯著，非線性因子模型[RMSE]值為0.324，比FF三因子模型的PMSE值小（見表5），說明本文提出的模型解釋效果更好。

七、結論

本文提出一種新的估計方法，構建加權非線性因子模型，研究公司特征與股票收益率存在的非線性關系以及模型的解釋力度，能有效解決維度詛咒問題，適用于公司特征數較多、無法構建投資組合及高維面板數據的情況，豐富了我國股票收益率和公司特征存在非線性關系方面的研究。

本文選取了1995年7月—2020年6月我國A股上市公司的財務數據，考慮公司規模特征、價值特征和動量特征，把這些特征的未知函數作為因子載荷，時變因子收益作為權重，采用格點法將特征函數映射到格點區間內，用高斯核估計條件期望，通過對高維數據不斷迭代估計參數，從而實現降維，同時估計出特征函數和因子收益，得到回歸結果。結果發現，特征函數滿足識別條件，是單調遞增的，其中動量特征和收益率是非線性關系。我們還通過計算模型的[UR2]研究了模型的解釋力度，發現市場因素在解釋股票收益率上占主要地位，其次是規模特征、動量特征和價值特征，回歸結果中這三個特征是顯著的。此外，本文還將中美兩國股票市場進行對比，研究發現本文提出的模型更加適用于中國，解釋力度更大;將本文的模型和FF三因子模型進行對比，發現FF三因子模型構建的所有投資組合中市場因子均顯著，而在有些投資組合中規模因子和價值因子不顯著，而且估計誤差比本文模型更大，說明本文模型的解釋效果比傳統三因子模型更好。本文提出的非線性因子模型，有助于通過基本面分析研究我國股市的超額收益，也能為金融市場的多因子投資策略提供參考建議。

參考文獻：

[1]Fama E F，French K R. 1993. Common Risk Factors in the Returns on Stocks and Bonds [J].Journal of Financial Economics，33.

[2]宋光輝，董永琦，陳楊煬，許林.中國股票市場流動性與動量效應——基于Fama-French五因子模型的進一步研究 [J].金融經濟學研究，2017，（01）.

[3]齊岳，周藝丹，張雨.公司治理水平對股票資產定價的影響研究——基于擴展的Fama-French三因子模型實證分析 [J].工業技術經濟，2020，（04）.

[4]張少華，陳慧玲.全要素生產率是有效的資本資產定價因子嗎？——基于中國股市的Fama-French因子模型檢驗 [J].中國經濟問題，2021，（02）.

[5]李雙琦，陳其安，朱沙.考慮消費與投資者情緒的股票市場資產定價 [J].管理科學學報，2021，（04）.

[6]周學偉，付巾書，宋加山.不同的政策不確定性對股市波動影響相同嗎？ [J].金融發展研究，2020，（05）.

[7]干偉明.基于多因子資產定價模型的A股市場配對交易策略研究 [J].金融理論探索，2018，（06）.

[8]周亮.基于隨機森林模型的股票多因子投資研究 [J].金融理論與實踐，2021，（07）.

[9]田利輝，王冠英.我國股票定價五因素模型：交易量如何影響股票收益率？ [J].南開經濟研究，2014，（02）.

[10]Connor G，Hagmann M， Linton O. 2012. Efficient Semiparametric Estimation of the Fama-French Model and Extensions [J].Econometrica，80（2）.

[11]Sharpe W F. 1964. Capital Asset Prices：A Theory of Market Equilibrium under Conditions of Risk [J].The Journal of Finance，19（3）.

[12]Lintner J. 1965. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets [J].Review of Economics and Statistics，47（1）.

[13]Lintner J. 1965. Security Prices，Risk，and Maximal Gains from Diversification [J].The Journal of Finance，20（4）.

[14]Carhart M M. 1997. On Persistence in Mutual Fund Performance [J].The Journal of finance，52（1）.

[15]Pastor L，Stambaugh R F. 2003. Liquidity Risk and Expected Stock Returns [J].Journal of Political Economy，111（3）.

[16]Novy-Marx R. 2013. The Other Side of Value：The Gross Profitability Premium [J].Journal of Financial Economics，108（1）.

[17]Fama E F，French K R. 2015. A Five-Factor Asset Pricing Model [J].Journal of Financial Economics，116（1）.

[18]Fama E F，French K R. 2016. Dissecting Anomalies with a Five-Factor Model [J].The Review of Financial Studies，29（1）.

[19]Hou K，Xue C，Zhang L. 2015. Digesting Anomalies：An Investment Approach [J].The Review of Financial Studies，28（3）.

[20]Hou K，Xue C，Zhang L. 2015. A Comparison of New Factor Models [W].Working Paper Series，Ohio State University，Charles A. Dice Center for Research in Financial Economics，05.

[21]Barillas F，Shanken J. 2018. Comparing Asset Pricing Models [J].The Journal of Finance，73（2）.

[22]Sko?ir M，Loncarski I. 2018. Multi-Factor Asset Pricing Models：Factor Construction Choices and the Revisit of Pricing Factors [J].Journal of International Financial Markets，Institutions and Money，55.

[23]趙勝民，閆紅蕾，張凱.Fama-French五因子模型比三因子模型更勝一籌嗎——來自中國 A 股市場的經驗證據 [J].南開經濟研究，2016，（02）.

[24]李志冰，楊光藝，馮永昌，景亮.Fama-French五因子模型在中國股票市場的實證檢驗 [J].金融研究，2017，（06）.

[25]Liu J，Stambaugh R F，Yuan Y. 2019. Size and Value in China [J].Journal of Financial Economics，134（1）.

[26]Connor G，Linton O. 2007. Semiparametric Estimation of a Characteristic-Based Factor Model of Common Stock Returns [J].Journal of Empirical Finance，14（5）.

[27]Freyberger J，Neuhierl A，Weber M. 2020. Dissecting Characteristics Nonparametrically [J].The Review of Financial Studies，33（5）.

[28]Raponi V，Robotti C，Zaffaroni P. 2020. Testing Beta-Pricing Models Using Large Cross-Sections [J].The Review of Financial Studies，33（6）.

Are Company Characteristics and Stock Return in a Non-linear Relationship？

——Based on the Empirical Research of Chinese Stock Market

Wei Jie/Wen Xinyue

（School of Economics，Huazhong University of Science and Technology，Wuhan? ?430000，Hubei，China）

Abstract：Asset pricing has been overwhelmingly researched in finance. A weighted nonlinear factor model is established based on existing research results，with unknown functions of firm characteristics as factor loadings and time-varying factor returns as weights，to investigate whether there is a nonlinear relationship between stock excess returns and firm characteristics，and the applicability and explanatory strength of the model to China's stock market. The financial data of China's A-share listed companies from July 1995 to June 2020 are selected，and the characteristic functions and factor returns are estimated simultaneously by using kernel function regression method considering firm size characteristics，value characteristics and momentum characteristics，and it is found that all three characteristics are significant and the momentum characteristics are nonlinearly related to the returns. In addition，the model in this paper is more applicable to the Chinese stock market and has stronger explanatory power compared to the US stock market; compared with the Fama-French three-factor model，the estimation error in this paper is smaller. The model proposed in this paper has implications in the field of fundamental analysis and factor investment strategies.

Key Words：stock market，weighted nonlinear factor model，nonparametric estimation，asset pricing

（責任編輯? ? 關? ?健;校對? ?LY，WY）

收稿日期：2021-12-09? ? ? 修回日期：2022-01-21

作者簡介：魏杰，男，華中科技大學經濟學院副教授，研究方向為微觀計量經濟學、因子模型;文欣玥（通訊作者），女，華中科技大學經濟學院，研究方向為資產定價。