小型無人機遙控器信號參數估計方法?

陳 林 唐文波 丁學科 樊 榮

（1.同方電子科技有限公司 九江 332000）（2.中國民用航空飛行學院航空電子電氣學院 廣漢 618307）

1 引言

近年來，各類民用無人機已在農業、電力、測繪、航拍、疫情防控等領域發揮著重要作用［1］。然而小型無人機具有易制造、易獲取、易改裝、易使用等特點，使得對小型無人機改裝等行為難以監管，因無人機非法應用導致的安全事件日益增多。同時，由于小型無人機具有典型的“低-慢-小”目標特性，當前的無人機信號檢測技術尚存在諸多問題，需要研究新的無人機目標檢測技術以解決對無人機目標信號檢測、識別和管控問題。

目前無人機目標檢測技術主要有雷達檢測［2］、聲波檢測［3］、光電檢測［4］等手段，但上述各檢測手段均存在技術缺陷。具體上講，雷達檢測需主動發射探測波形，在民航機場凈空區域無人機目標探測應用中存在無線電頻譜兼容問題，且無人機回波特征與飛鳥回波特征相似，目標難以辨識。聲波檢測技術手段主要憑借無人機在工作時電機（或旋翼）產生的聲音信號（一般涵蓋300Hz～20KHz頻率范圍），利用聲紋識別技術對無人機目標檢測和識別，但該類方法的目標探測距離一般在幾十米范圍內。光電檢測技術手段主要利用可見光/紅外成像技術通過圖像識別算法實現無人機目標檢測，該類技術受實際光線、溫濕度等環境因素影響明顯。與上述幾種檢測手段不同，利用無人機與遙控器間的控制信號對無人機目標檢測，具有顯著的技術優勢［5］。當前小型無人機遙控器信號頻率主要集中在 IEEE 802.11 WLAN 工 作 頻 段［6］（2.4GHz～2.483GHz頻率范圍），普遍采用跳頻擴譜（Frequen?cy-Hopping Spread Spectrum，FHSS）用頻方式。通過提取無人機遙控器信號的跳頻速率、跳頻時刻、跳頻頻率等特征可有效檢測無人機目標，對無人機遙控器信號跳頻參數估計已成為當前無人機目標信號檢測與識別的重要技術手段［7～8］。

針對跳頻擴譜（FHSS）信號檢測，代表性方法主要是基于時頻分析的信號檢測法。在該類方法中，作為最具代表性的短時傅里葉變換（Short Time Fourier Transform，STFT）法已被廣泛應用于跳頻信號參數估計中，該方法屬于線性時頻變換分析方法范疇，具有運算復雜度低、實時性高等優點，但對信號參數的估計精度不足［9］。在此基礎上，He Y.等人提出了一種跳頻周期和跳頻頻率聯合估計方法，提升了跳頻信號參數的估計性能，但該方法仍然屬于線性時頻分析方法，所能獲得的信號時頻分辨能力有限［10］。對此，Barbarossa采用維格納-維利分布（Wigner-Willie Distribution，WVD）估計信號的跳頻頻率和跳頻時刻，提升了對信號的時頻分辨能力，但多個信號同時存在時，該方法會產生交叉干擾項問題，從而限制了該方法的信號特征提取能力［11］。鑒于上述問題，新的基于偽維格納-維利分布（Pseudo Wigner-Willie distribution，PWVD）［12］和平滑偽維格納-維利分布（Smooth Pseudo Wigner-Willie Distribution，SPWVD）［13］的時頻分析檢測方法被相繼提出，抑制了交叉項干擾，進一步提升了對調頻信號的時頻特征分析能力，然而這兩種方法存在時頻聚集性不高的問題，在實際應用中受到一定限制。為提升時頻聚集性，張曦等基于Gabor變換提出了一種對跳頻信號參數估計的時頻分析方法，該方法在消除交叉干擾項的同時保留了信號的時頻聚集特性，然而所提方法的計算復雜度高，難以應用在高實時性要求場景中［14］。為進一步提升時頻分析性能，付衛紅等將STFT和SPWVD相組合，提出了一種新的時頻分析方法［15］，此外，Stock?well R G等人基于S變換也實現了對跳頻信號參數提取并獲得了不錯的性能［16］。然而上述各類信號檢測方法未設計專門的噪處理環節，對此劉若蘭等在時頻分析基礎上引入門限降噪策略對噪聲進行抑制，提高了信號時頻參數估計性能［17］。需指出的是由于檢測方法中人為引入了降噪門限，設置的靜態門限難以應對復雜動態變化的信號檢測場景。

考慮到當前各類跳頻信號參數估計方法均存在各自缺點（時頻參數估計性能差，計算復雜度高，或環境適應能力弱等），本文針對無人機遙控器信號檢測應用場景，提出了一種計算復雜度低且檢測性能好的跳頻信號參數估計新方法。所提方法無需計算無人機跳頻信號的時頻分布信息，而是基于頻域互相關運算降低了檢測方法的計算復雜度。同時，在信號參數估計中無需預先人為設定門限閾值，通過分析相鄰段采樣信號的頻域相關性即可檢測信號頻率是否發生跳變，提高了跳頻信號特征估計性能。

2 跳頻信號模型

工作在2.4GHz頻段的小型無人機遙控器信號普遍采用跳頻通信模式，跳頻信號是一種典型的非平穩信號，其載波頻率通常按照通信雙方約定的規律隨著時間跳變。單個跳頻信號的載波頻率在某一跳頻周期內保持不變，所有可能出現的載波頻率構成了該跳頻信號的跳頻頻率集合，典型跳頻信號的時域模型如下［18～19］：

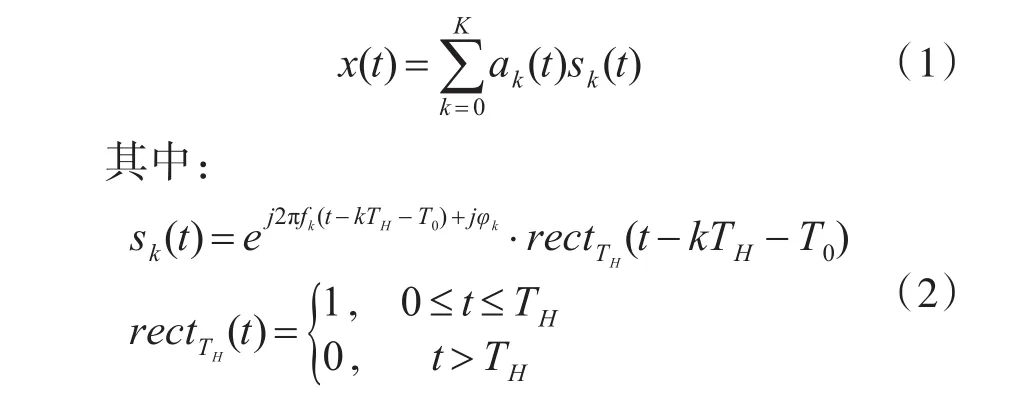
式（1）中的K為跳頻次數；ak(t)為分配到第k個跳頻載波頻率上的基帶信號；式（2）中的sk(t)、fk、φk分別表示第k個跳頻信號分量及其瞬時頻率和初始相位；rectTH(t)表示寬度為TH的門函數；TH為跳頻周期；T0為起跳時刻。

在均值為0方差為σ2的復高斯白噪聲噪聲場景（記噪聲為v(t)）中，經過對信號離散采樣后的N點離散信號觀測值建模為

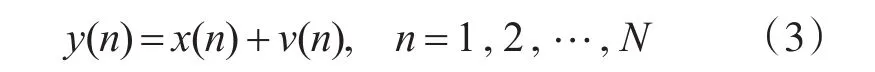
其中，隨機噪聲v(n)～(0，σ2)。

3 跳頻信號參數估計方法

考慮到基于STFT的時頻分析方法具有復雜度低，實時性高等有點，本文選取了兩種基于STFT為基礎的代表性時頻分析方法作為所提方法的對比方法。在具體給出兩種傳統檢測方法之前，STFT及時頻圖計算表達式。

對于任意給定的離散時域信號序列｛y(n)|n=1，2，…，N｝，其短時傅立葉變換計算式可通過式（4）得到［22］：

式中h(l)為窗函數；Len為窗口的寬度；l表示離散時間點；u表示離散頻率點。將STFT結果取模平方的結果定義為時頻譜圖，數學模型表示為

1）方法1：基于時頻脊線的跳頻參數估計

在該方法中，通過提取時頻脊線得到無人機跳頻信號在不同時刻的頻率值，將不同頻率值間的時間間隔作為信號的跳頻周期值，其倒數即為跳頻速率，并將頻率值發生改變的時刻記為跳頻時刻；取信號某一跳的跳頻周期內所有頻率值的均值作為該跳信號的頻率值。基于時頻脊線的跳頻參數估計法算法流程如圖1所示。

圖1 基于時頻脊線的跳頻參數估計法

2）方法2：基于最大值圖的跳頻參數估計

基于最大值圖的跳頻參數估計法中，首先沿時隙逐點找出頻率軸上的最大值，得到具有周期性的最大值圖R(m)，在此基礎上計算相鄰峰值間的距離作為信號跳頻周期的估計值；然后利用二次差分算法估計每跳信號的中心時刻；最后通過每跳的中心時刻進一步估計出跳頻時刻集和跳頻頻率集。完成對無人機遙控器調頻信號的參數估計。該檢測方法的算法流程如圖2所示。

圖2 基于最大值圖的跳頻參數估計法

3）所提方法：基于頻域互相關的跳頻信號參數估計

注意到同一架無人機跳頻信號的每跳信號具有相同帶寬，利用頻域互相關處理可在頻域上獲得高相似性的能量分布特征，因此基于該特性可以完成對無人機遙控器跳頻信號參數估計。通過預先在時域上按時隙分割信號進而分析相鄰信號的頻域相關性，即可判定信號頻點是否發生跳變，進而估計出無人機跳頻信號的各類特征參數。為展示該特性，下面基于前文給出的跳頻信號模型生成仿真數據，假設無人機遙控器信號的頻率變化范圍為20KHz～80KHz，頻率間隔為15KHz，跳頻周期為2ms，采樣頻率為400KHz，采樣時間為0.1s，信號劃分時隙為1ms（對應樣本點數L為400），信噪比為0dB。

基于上述參數場景計算了同一架無人機相鄰跳信號的頻域圖及其頻域相關結果，圖3為仿真結果。同時，還計算了同一架無人機信號在相同跳內不同時刻的頻域圖及其頻域相關結果，圖4為仿真結果。

圖3 相鄰跳的跳頻信號頻域及頻域相關結果圖

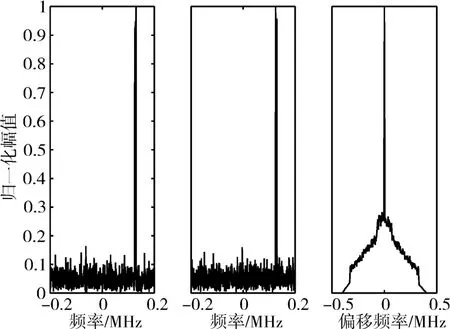
圖4 同一跳的跳頻信號頻域及頻域相關結果圖

圖3 和圖4的仿真計算結果表明：當信號頻域相關結果中的峰值出現在零頻點附近時，則兩段信號屬于同一跳信號內的前后相鄰時隙信號；而峰值出現在非零頻點時，則表明前后兩段信號的頻率發生了跳變，即兩段信號具有不同頻點。基于上述特征，下面給出一種基于信號頻域互相關的跳頻信號參數估計方法，所提方法詳細的信號參數估計流程如圖5所示。

圖5 基于頻域互相關的跳頻參數估計法

4 仿真實驗與分析

4.1 評價指標

為評價所提方法的跳頻信號參數估計性能，使用相對誤差（Relative Error，RE）作為跳頻速率參數估計的評價指標，相對誤差定義式如下。

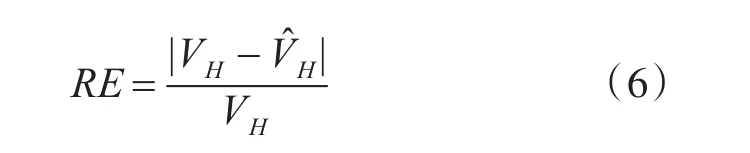
式中為跳頻速率估計值，VH為真實跳頻速率。

使用為評價所提方法的跳頻時刻集和跳頻頻率集參數估計性能，文中使用均方根誤差（Root Mean Square Error，RMSE）作為評價指標，定義式為

4.2 仿真實驗

仿真場景設置如下：跳頻信號的頻率變化范圍為20KHz～80KHz，頻率間隔為15KHz，跳頻周期為2ms，采樣頻率為400KHz，采樣時間為0.1s，信噪比變化范圍為-10dB～8dB，在每個信噪比場景下進行1000次蒙特卡洛仿真實驗。

三種方法的計算耗時如圖6所示，跳速估計誤差、跳頻時刻集估計均方根誤差、跳頻頻率集估計均方根誤差分別如圖7～圖9所示。

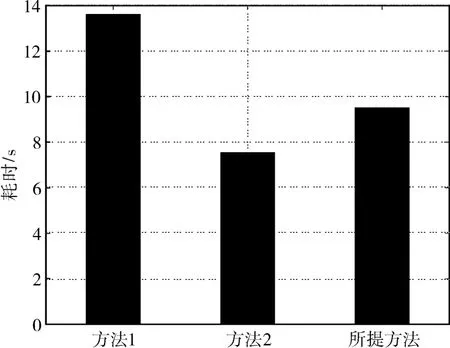
圖6 三種方法計算耗時（1000次蒙特卡洛）

從圖7的跳頻速率估計誤差結果中可以得知，所提方法在信噪比極低的場景下性能與方法1和方法2相當，但當信噪比大于-2dB時，前者對跳頻速率參數的估計性能大幅提升，且當信噪比大于2dB后誤差達到了最小值并趨于穩定。

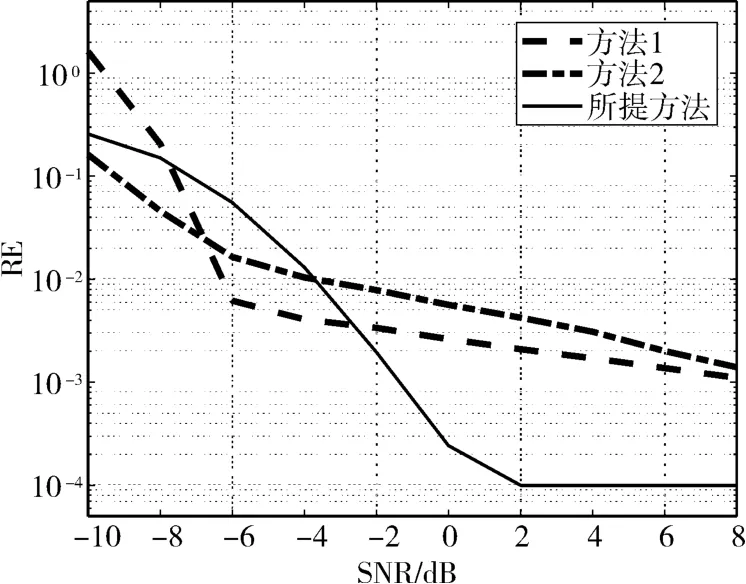
圖7 跳頻速率估計誤差

圖8中的跳頻時刻集估計均方根誤差結果表明：所提方法的性能幾乎全面優于方法1和方法2。與方法1和方法2不同，所提方法在信噪比大于-6dB的場景下，對跳頻時刻集參數的估計性能顯著提升。

圖9為三種方法對跳頻頻率參數的估計結果，傳統方法的估計誤差在極低信噪比下有著極大的誤差，當信噪比達到-6dB時性能得到巨幅提升，這直觀地反映出閾值的設定給傳統方法帶來的弊害。而所提方法對噪聲的敏感度較低，當信噪比大于0dB后參數估計性能趨于穩定且優于傳統方法。

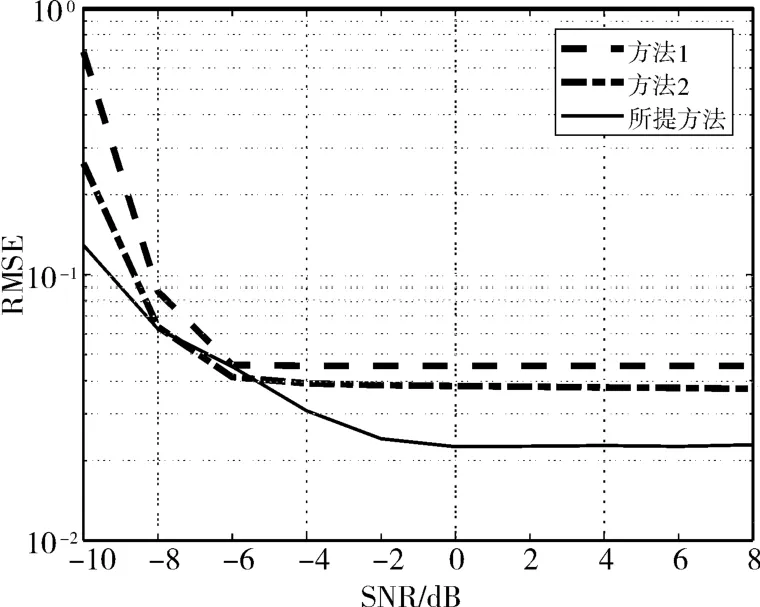
圖9 跳頻頻率集估計誤差

仿真結果表明當信噪比大于-2dB時，本文所提方法在跳速參數估計、跳頻時刻集參數估計、跳頻頻率集參數估計上全面優于方法1和方法2，對無人機跳頻信號的特征參數有著優秀的估計性能，并在信噪比大于2dB時，參數估計性能趨于穩定。

5 結語

本文為提高跳頻信號特征參數估計性能，針對跳頻信號中每跳信號的頻率特征，提出了一種基于頻域互相關的跳頻信號特征參數估計方法。該方法與傳統的時頻分析方法相比，在降低運算量的同時解決了由于閾值的設定導致在低信噪比場景下帶來的檢測性能下降的問題。仿真結果表明，本文所提方法對跳頻信號的跳頻速率、跳頻時刻集、跳頻頻率集的估計性能優于傳統的基于時頻脊線的特征參數估計法和基于最大值圖的跳頻參數估計法。接下來主要研究工作是利用所提方法在采樣帶寬受限條件下實現無人機跳頻信號檢測與參數估計。