風驅海面和艦船尾跡軌道速度場的快速重建方法

李宇鑫, 劉 鵬, 顧丹丹

(1.復旦大學電磁波信息科學教育部重點實驗室,上海 200433;2.電磁散射重點實驗室,上海 200438)

0 引言

合成孔徑雷達(synthetic aperture radar,SAR)可對大范圍海面進行遠距離、全天候的觀測,具有無可替代的優(yōu)勢,在海洋遙感領域得到了廣泛的應用。在高分辨SAR圖像中,艦船及其產(chǎn)生的尾跡非常明顯,利用SAR圖像實現(xiàn)艦船探測和定位越來越受到重視。但是海面的多變性和復雜性影響了艦船檢測,尤其在海況等級高時,海面粗糙度增加,極大地增加了艦船的誤檢率。而尾跡相比于艦船尺度更大,利用尾跡可更準確地估計艦船的實際位置、航速和航向,對于小船或海況等級高時的艦船檢測也具有獨特的優(yōu)勢。

海面的波高場和流體微元(亦稱水質點)的軌道速度場對SAR成像至關重要。目前常采用流體動力學計算軟件獲取海面波高場和軌道速度場數(shù)據(jù)。FUJIMURA等基于FLUENT軟件建立了二維和三維的尾跡模型。WANG等采用OpenFOAM軟件得到了艦船尾跡的波高和軌道速度。文獻[8]提出了基于最小二乘(least square quadratic,LSQ)方法的艦船尾跡和海面軌道速度場重建方法,該方法解決了SAR成像仿真中軌道速度場建模的關鍵問題。然而,LSQ方法求解線性方程組時的矩陣運算導致重建速度慢,且計算復雜度為()量級。本文通過傅里葉(Fourier)分析,利用快速傅里葉變換(FFT)實現(xiàn)海面軌道速度場的快速重建,實現(xiàn)計算復雜度為()量級的軌道速度場重建。

本文首先根據(jù)線性波理論得到波高場(wave height field,WHF)和軌道速度場(orbital velocity field,OVF)的理論計算公式;然后利用流體動力學計算軟件得到波高場,基于FFT實現(xiàn)波高場和軌道速度場的重建,并從理論上分析重建的計算復雜度;在數(shù)值結果部分,根據(jù)海譜模型和線性波理論,分別計算風驅海面的波高場和軌道速度場;最后驗證風驅海面和艦船尾跡的軌道速度場重建的正確性和快速性,并分析FFT方法存在的問題。

1 海譜模型

風驅海面的幾何建模一般基于海譜模型。為了在風驅海面條件下驗證基于FFT重建方法的正確性,首先基于海譜模型得到風驅海面的軌道速度場。海浪方向譜描述了海浪內(nèi)部能量相對于頻率和方向的分布。將海浪方向譜函數(shù)記為(,),其一般可表示為海浪頻譜函數(shù)()和方向分布函數(shù)(,)的乘積,具體表達式為

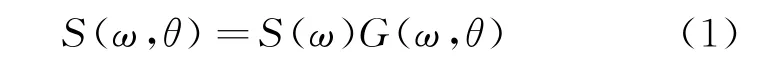
式中:是海浪的角頻率;是傳播方位角。

本文采用經(jīng)典的P-M譜和波浪立體觀測計劃(stereo wave observation project,SWOP)得到的方向分布函數(shù)進行海浪方向譜建模。

Pierson和Moskowitz于1964年對北大西洋充分成長狀態(tài)下的風浪記錄數(shù)據(jù)進行譜估計,將得到的54個譜依風速分成5組,并將各組譜進行了平均,得到P-M譜函數(shù)

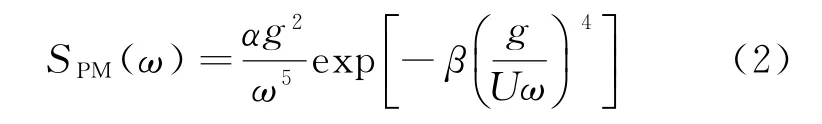
式中:0.008 1是無因次常數(shù);是重力加速度;0.74是經(jīng)驗常系數(shù);是距海平面19.5 m高處的風速。P-M譜是以風速為參量的充分成長狀態(tài)的海浪頻譜。相比于其他海浪譜,P-M譜數(shù)據(jù)基礎較好,準確性更高,而且更符合傅里葉譜的定義,因此被廣泛應用。

SWOP得到的方向分布函數(shù)

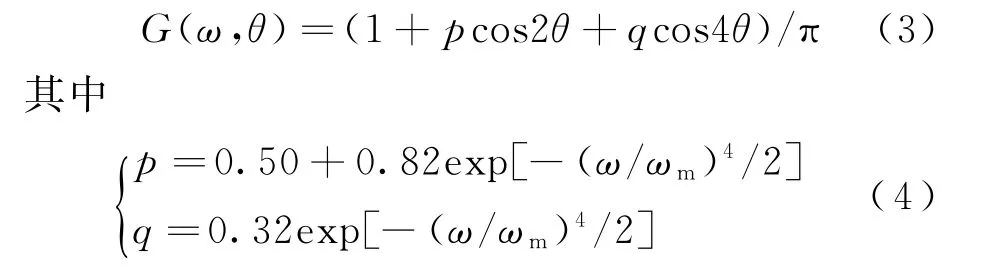
式中:=8.565/為譜峰頻率。

2 波高場和軌道速度場的數(shù)值計算

2.1 線性波理論

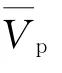
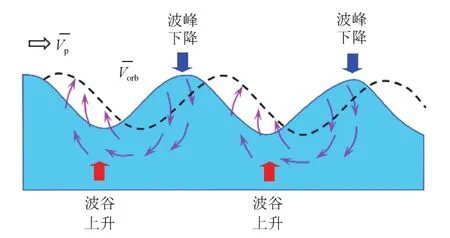
圖1 海面長波的傳播與水體內(nèi)水質點的軌道運動

2.2 風驅海面和艦船尾跡的軌道速度場

2.3 FFT與LSQ計算復雜度比較

仿真用計算機內(nèi)存4 GB,采用Fortran軟件實現(xiàn)不同采樣點數(shù)場景的OVF重建。采用LSQ和FFT方法的OVF重建時間如圖2所示。可以看到,LSQ方法重建耗時約為FFT方法的3倍。因此,采用FFT方法進行OVF重建,可以提高重建速度。

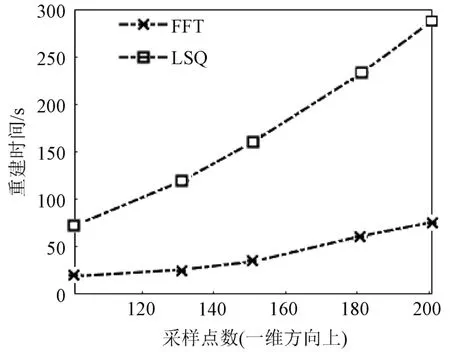
圖2 LSQ和FFT的OVF重建時間曲線

3 軌道速度場的重建與驗證

在海面風速10 m/s、風向0°條件下,基于線性波理論和FFT方法進行OVF重建,結果如圖3所示。海面網(wǎng)格節(jié)點處軌道速度矢量的方向和大小用箭頭指示。根據(jù)經(jīng)典的線性波理論求得的風驅海面OVF如圖3(a)所示。將風驅海面理論波高輸入FFT重建程序,得到的重建OVF如圖3(b)所示。

圖3 風驅海面的軌道速度場

對比圖3(a)與圖3(b)中的速度矢量,并以均方誤差來衡量重建結果的準確性。由于邊緣的截斷效應,在計算誤差時將海面邊緣范圍縮小一個最短波長。均方誤差

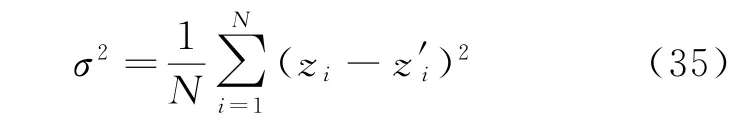
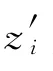
柯林斯(Collins)級潛艇模型在水深6 m處,以10 kn(5.144 m/s)的速度運動時的尾跡波高場如圖4所示。模型艇長78.245 m,艇寬13.000 m,排水量3 324.5 m。

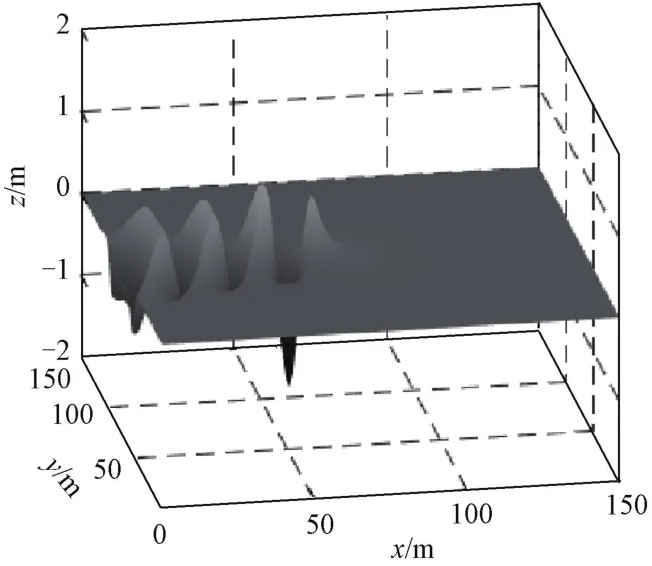
圖4 艦船尾跡的波高場

圖5是基于FFT重建的風驅海面與艦艇尾跡疊加場景下的軌道速度場矢量圖。

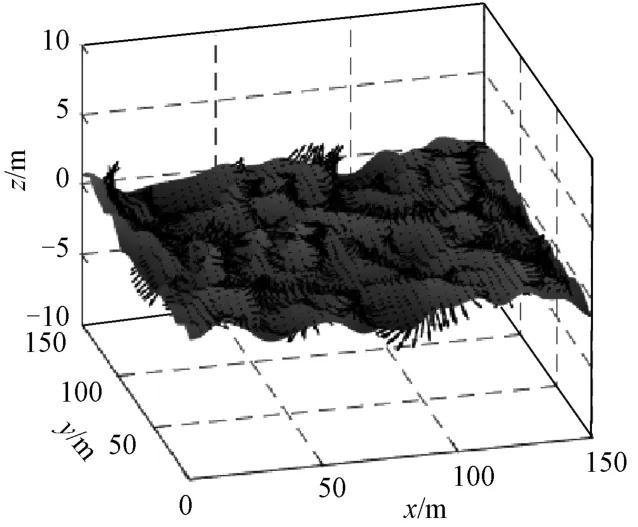
圖5 風驅海面及艦船尾跡的軌道速度場

通過比對圖5和圖3可以看出:圖3中波峰處矢量方向大致沿方向,與風向基本一致,即沿波的傳播方向,符合軌道速度的定義;圖5中左邊部分由于疊加了沿方向前進的目標尾跡,該位置明顯可見朝向方向的矢量,即與目標前進方向一致,這驗證了本文風驅海面和艦船尾跡疊加后軌道速度場重建方法的正確性。

4 結論

本文基于線性波理論,采用FFT實現(xiàn)了風驅海面及艦船尾跡軌道速度場的快速重建。通過比較海浪譜模型和基于FFT重建的軌道速度場仿真結果,驗證了基于FFT重建方法的正確性。

由于離散傅里葉變換存在頻譜泄漏的固有缺陷,基于FFT重建的海面軌道速度場模型中,海面邊緣非整周期的截斷將引入高頻分量,因此誤差較大的邊緣區(qū)域應予以棄用。