階躍載荷下氣體軸承-轉子系統瞬態特性流固耦合分析*

丁 一 馬文琦 孫培耕 邱習強

(大連海事大學船舶與海洋工程學院 遼寧大連 116026)

機床加工過程中，主軸精度是影響產品質量的關鍵因素，氣體軸承-轉子系統是主軸系統中的關鍵部件。在瞬態變載荷工況下，氣體軸承-轉子系統中的轉子運動與氣膜流場間存在強耦合作用，對氣體軸承-轉子系統進行流固耦合瞬態特性分析，有助于研究系統受瞬變載荷瞬間的系統響應，對指導實際加工，提高加工精度有重要意義。吳斌[1]基于流固耦合法，針對靜壓止推軸承在承載過程中氣膜間隙的變化，給出了主軸高速旋轉時的承載力特性曲線。WANG等[2]采用有限體積法給出了流固耦合作用下氣膜間隙在不同負載下的非線性振蕩特性。YU等[3]采用流固耦合的手段預測了滑動軸承在重載下因系統結構形變而造成的油膜間隙沿半徑方向的變形規律。WODTKE等[4]使用流固耦合的方法，研究了水潤滑軸承的動靜壓效應和固體變形對流場壓力的影響。趙自強[5]建立了軸承-轉子系統流體-固體耦合模型，并在CFD分析軟件中運用流固耦合法對該模型進行流固耦合分析計算，進而獲得主軸的變形量以及變形引起的靜壓氣體軸承靜態特性的變化。針對靜壓徑向軸承在承載過程中出現的軸頸傾斜現象，楊彥濤和王海博[6]采用理論分析結合MATLAB仿真的方法研究了不同傾斜角下轉子系統承載特性的變化，得到了一定偏心率下傾斜角度和承載力等特性的變化規律。JENG和HUANG[7]研究了不同材料對軸承動態特性的影響規律并總結了不同轉速、潤滑條件、工作載荷下軸承動態特性的變化規律。JORGENSEN和SHIN[8]對軸承-轉子系統進行動力學建模并研究了不同切削載荷、進給速度及旋轉速度下系統動態特性的變化規律。對于階躍載荷對轉子系統的影響，何芝仙等[9]選擇使用ADAMS和MATLAB聯合仿真的手段，研究了油潤滑軸承受到階躍載荷沖擊時的動力學響應和軸承的摩擦學特性。LAI等[10]分析了軸承結構剛度和阻尼特性對轉子-箔片-軸承系統穩定運行的影響，通過靜載荷和撓度試驗，得到了徑向滑動軸承和推力軸承的靜態結構剛度和阻尼系數。李昊等人[11]從超調量、超量時間和軸心偏心量等角度分析了可傾瓦軸承在階躍載荷下的動態響應。關岱杉和郭百森[12]通過有限差分法求解動載滑動軸承的雷諾方程，對比分析了階躍、正弦、孤峰波形沖擊作用下滑動軸承油膜壓力分布特征。田尚沛[13]以高速電主軸為研究對象分析了轉速、預緊力、軸承參數以及熱變形之間的關系。ZHANG等[14]研究了預緊力對轉子-軸承系統振動的影響，結果表明預緊力對系統振動大小有不可忽視的影響。李純潔等[15]將實驗與仿真相結合，得出不同轉速下軸承預緊力對軸承動剛度的影響規律，進而指出可以通過調節預緊力以增強軸承剛度。

目前大多數學者在研究氣體軸承-轉子系統時往往忽略氣體軸承支承氣膜流場與轉子運動姿態之間的流固耦合作用及實際工況下負載瞬態激勵對轉子軸心偏移的影響。因此，本文作者以氣體軸承-轉子系統為研究對象，通過雙向流固耦合數值仿真，分析不同階躍載荷激勵下軸承氣膜流場不同時刻下的壓力分布特性，以及氣體軸承-轉子系統的轉子超調量、超調時間、穩定時間等特性的影響因素和變化規律。

1 流固耦合仿真模型建立

1.1 系統模型

氣體軸承-轉子系統結構如圖1所示，采用環面節流形式的徑向氣體軸承，止推氣體軸承和徑向止推聯合氣體軸承構成了系統中的軸承組。軸承-轉子系統在高轉速運轉及承受負載條件下，氣膜流場特性與轉子偏移、受力分布相互影響，因此需對其進行雙向流固耦合分析。銑削過程中，轉子受到銑刀銑削工件帶來的力簡化為y方向的載荷F。當轉子受載后，處于傾斜狀態，轉子中心線如圖1中虛線所示。兩端徑向軸承承載力分別為W1和W2，結構參數如表1所示。

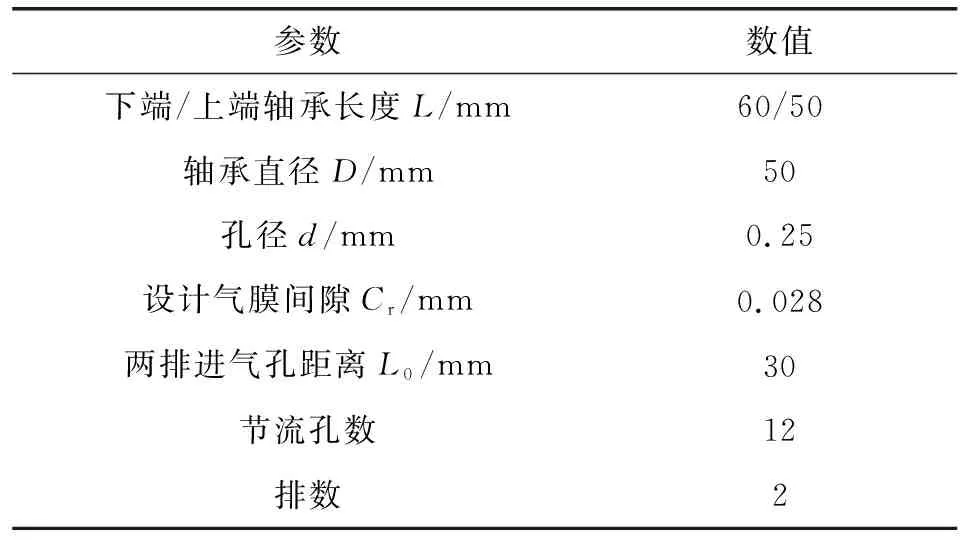
表1 徑向軸承結構參數Table 1 Structural parameters of radial bearing

1.2 網格劃分及求解設置

圖2(a)和圖2(b)所示分別為轉子和氣膜流場模型。流場的三維模型由多個部分組成，分別為徑向止推氣體軸承、止推氣體軸承和徑向氣體軸承氣膜模型。轉子建模過程中，單獨建立與流場對應的耦合面，以方便進行流場與固體場之間的數據傳輸。轉子固體場網格全部采用結構性網格；采用分區畫法將流場網格分為氣膜與節流孔兩部分，其中氣膜網格分成12個區域，采用結構性網格，節流孔區域附近采用非結構性網格，并進行網格加密。

以徑向軸承節流孔附近壓力分布及承載力為無關性驗證對象，對比分析網格數分別為77萬、120萬與200萬的仿真計算結果。結果發現，77萬網格數量時的承載力與其他2種網格數量時相差較大，120萬網格數與200萬網格數的節流孔附近壓力分布及承載力的計算結果偏差較小。考慮計算效率和網格數對數值仿真結果的影響，文中采用120萬網格數進行數值仿真。

流固耦合模型邊界條件及相關參數設置如下：

(1)外部環境壓力p0=0.101 MPa，環境溫度T0=300 K，流體介質選擇理想氣體；

(2)轉子和流場的接觸面設置為流固耦合數據傳輸面，節流孔入口供氣壓力ps=0.6 MPa(相對壓力)，流場出口壓力為環境壓力p0；

(3)選擇離散、隱式求解器，湍流模型為SSTk-ω模型。

2 階躍載荷下軸承-轉子系統瞬態響應分析

2.1 轉子動態響應分析

銑刀與工件接觸瞬間所產生的階躍載荷將導致轉子刀頭位置突變，使氣膜瞬間產生壓縮，嚴重時會出現抱軸現象。為了研究銑削過程中轉子的動態特性，對簡化后的轉子下端刀頭位置施加圖3所示的穩態和矩形2種類型階躍載荷。

以上升時間tr、超調時間tp、最大超調量Mp和穩定時間ts等系統瞬態響應參數作為性能指標的系統,在階躍載荷作用下位移響應特性曲線如圖4所示。

圖5所示為上、下端徑向軸承在200 N階躍載荷作用下，承載力隨時間的變化。結果顯示，上、下軸承支承承載力都出現振蕩過程，超調分別達到了497.5和142.3 N，振蕩后達到平衡。此時，上下端徑向軸承的承載力方向相反且下端軸承承載力大于上端徑向軸承。文中以下端徑向氣體軸承為主要研究對象，分析系統在階躍載荷下的瞬態響應特性。

圖6所示為不同階躍載荷下轉子位移響應，3個時刻分別代表系統超調過程中的最大偏移時刻TA、最小偏移時刻TB和穩定時刻TC。對比結果可看出，在不同階躍載荷作用下，轉子位移響應變化規律一致，200 N階躍載荷作用下，轉子偏移幅值明顯大于100 N階躍載荷，且階躍載荷越大，轉子超調量、最大振幅越大，調節穩定后轉子偏斜位移值增大，但系統的超調時間tp和最終的穩定時間ts都有所縮短，穩態階躍載荷下系統的動態特性參數如表2所示。

分析圖6中矩形階躍載荷作用下轉子刀頭處的位移變化和表3中矩形階躍載荷的超調時間tp可知：在0～10 ms階段，100 N穩態階躍載荷與矩形階躍載荷下轉子動態響應變化規律基本一致，經過6.5 ms后達平衡位置。在t=10 ms時刻，外負載在從100 N階躍到200 N，轉子經過4.1 ms后到達平衡位置，與200 N下穩態階躍載荷相比，二次階躍載荷下轉子響應更快，滯后性較低。

相比200 N穩態階躍載荷下的動態特性，10～20 ms階段，矩形階躍載荷下系統性能提高比例如表4所示。

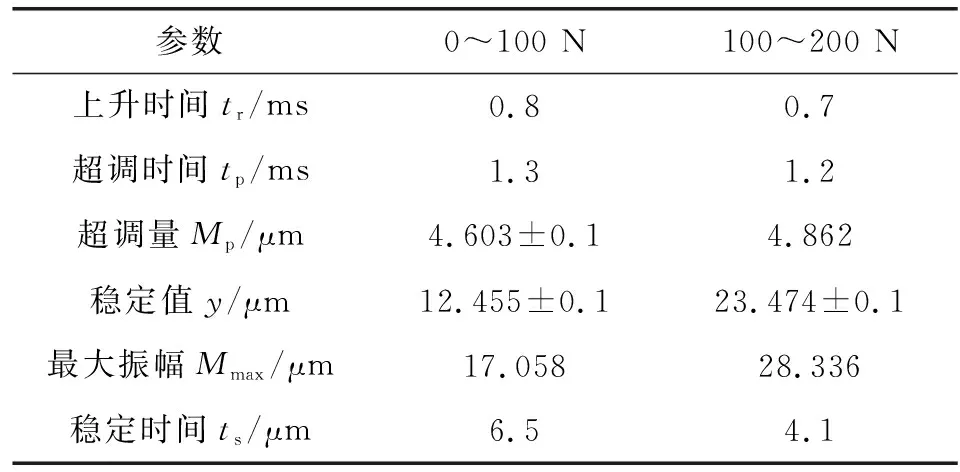
表3 矩形階躍載荷下系統動態特性參數Table 3 System dynamic characteristic parameters under rectangular step load

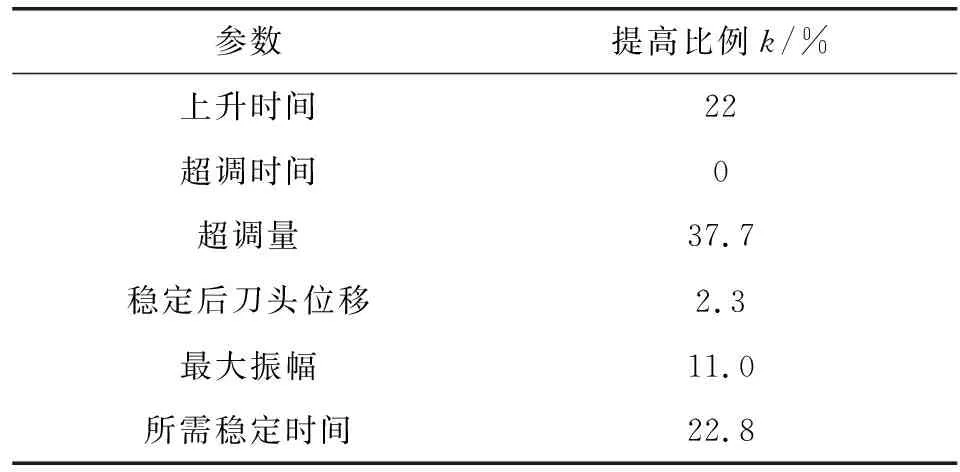
表4 矩形階躍載荷下系統性能提高比例Table 4 System performance improvement ratio under the rectangular step load

由表4結果可知，矩形階躍載荷下系統穩定性能明顯提高。原因是矩形階躍載荷下，10 ms時系統已在外載荷的作用下達到耦合平衡，氣膜已經具有一定的剛性，系統也有一定抗載荷能力，在此基礎上外載荷突然增大，氣膜剛性抑制了轉子大幅度偏移，轉子超調量減小。故預載荷有助于提高系統瞬態響應下的穩定性。

2.2 軸承流場特性分析

圖7所示為轉子中心線在100～200 N矩形階躍載荷下的位移及形變。3個時刻同樣分別代表系統超調過程中的最大偏移時刻TA、最小偏移時刻TB和穩定時刻TC。結果顯示，在流固耦合過程中，受到載荷和氣體軸承承載力的共同作用轉子發生傾斜偏移和輕微彎曲變形現象。

圖8所示為不同時刻氣膜流場壓力云圖。從圖8(a)可以看出，軸承流場周向壓力變化明顯，沿轉子軸向偏斜導致氣膜厚度軸向的非均勻性，壓力分布沿軸向也出現非均勻現象，軸承下端傾斜帶來的更高的氣膜壓縮量導致流場壓力更高。圖8(b)和圖8(c)中氣膜壓力因轉子傾斜造成的壓力分布沿軸向非均勻性相對較弱。

圖9給出了矩形階躍載荷下承載力隨時間的變化。從圖7—9可以看出，伴隨著轉子因階躍載荷的超調偏移，氣膜間隙大小的波動直接影響了流場內的壓力分布，進而影響氣膜承載力隨時間的變化。

矩形階躍載荷下系統y向受力情況如表5所示。圖9中TA時刻下端徑向軸承承載力超調量最大，軸承y向承載力大于負載，因此轉子y向偏移量減小，向反方向偏移；至轉子偏移量最小的TB時刻，軸承y向承載力小于負載，轉子y向偏移量增大，在徑向軸承承載力與載荷的共同作用下，轉子往復振動直至趨于動態平衡狀態；在TC時刻，軸承y向承載力與負載相近，系統趨于平衡。

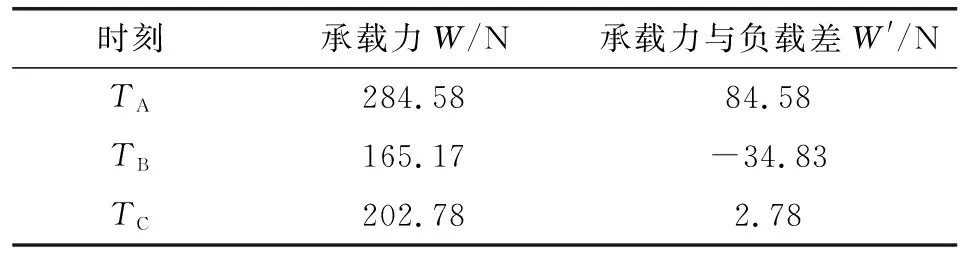
表5 矩形階躍載荷下系統y向受力變化Table 5 Variation of the y-direction force of the system under rectangular step load

圖10給出了200 N穩態階躍載荷和矩形階躍載荷在負載瞬變時的流場壓力變化。可知，在同樣承受200 N載荷的情況下，矩形載荷的超調時刻的壓力變化較小，僅在壓力等級為7以上的承載區域有略微的變化，壓力變化較為平穩; 而在200 N穩態階躍載荷下，壓力等級8以上的高壓區域出現明顯的壓力波動，反映到實際工況下將造成轉子軸心軌跡紊亂、加工精度降低等負面影響。從圖10(a)和圖10(c)可以看出，2種不同載荷形式下超調位置處流場的高壓區域出現明顯差別，圖10(c)所示的200 N穩態階躍載荷下壓力較大且高壓區域較廣，主要是由于此時氣膜壓縮量較大造成的。由上述分析可知，過高的壓縮量將會導致氣膜更劇烈的回彈進而影響轉子回轉精度，預載荷對于減小流場壓力波動從而增加轉子系統穩定性具有重要意義。

3 加載實驗

氣體軸承-轉子系統測試試驗臺如圖11所示。試驗臺主要包括氣體軸承-轉子系統、加載裝置、壓力控制采集系統以及位移信號采集系統。試驗臺中轉子位移、加載力信號和壓力信號采集與控制通過采集卡連接到計算機的LabView程序中。

圖12和圖13所示分別為200 N階躍加載和100～200 N矩形階躍加載試驗測試與數值仿真模擬結果對比曲線，其中T0為測試總時長。可知：試驗測試與仿真結果變化趨勢一致，但由于系統響應及測試誤差等原因，試驗偏移量曲線略滯后于仿真曲線。在200 N單一階躍加載條件下，試驗測試轉子最大偏移量為32.5 μm，穩定后偏移量約為27 μm，略大于仿真值。在100～200 N矩形階躍加載條件下，轉子最大偏移量為28.8 μm，相比200 N階躍加載試驗下最大偏移量減小3.7 μm，與仿真結論一致，即矩形階躍加載時氣膜已經具有一定的剛性，系統抗干擾能力更強，穩定性更好。

4 結論

(1)系統受載時，氣膜流場壓力分布沿軸向出現非均勻分布現象，轉子下端軸承處氣膜偏心更大，壓力更高，承載力更大。

(2)系統所受到的穩態階躍載荷增大時，雖然系統的超調時間和最終的穩定時間都有所縮短，但轉子超調量隨之增大，氣膜壓縮量增大，影響轉子回轉精度從而影響加工質量。

(3)矩形階躍載荷使得氣膜具有一定的剛性，進而使得流場壓力波動減小，轉子超調量明顯減小，且轉子的穩定時間也有所縮短，即預載荷能使系統在載荷瞬變情況下的剛性和抵抗能力明顯增強，有助于提高實際加工過程中的加工質量。