基于卡爾曼預測粒子濾波的復雜場景圖像目標跟蹤算法
張 博
(長沙師范學院 信息科學與工程學院,長沙 410100)
隨著計算機技術的興起與發展,計算機能夠對視覺信息進行相應的處理與應用,極大推動了計算機視覺的興起與發展, 受到了多個領域的關注,相對應的研究也逐漸增多。 在計算機視覺領域中,關鍵部分就是對動態圖像進行處理與分析,以此來獲取有效的、有用的信息。 動態圖像會隨著時間變化產生相應的變化, 并能夠表示為空間位置函數,存在著豐富的信息, 其處理過程涉及多種領域知識,例如圖像分析領域、計算機視覺領域、人工智能領域等。 動態圖像分析是現今計算機領域中發展較為活躍的分支,對其進行深入探究具有現實意義。
就現有研究成果來看,主流目標跟蹤算法主要包含7 類,分別為基于對比度的目標跟蹤算法(一種基于改進混合高斯模型的運動目標檢測算法[1]),該算法主要利用背景與目標之間的對比度對目標進行識別與跟蹤,優勢為對目標姿勢變化適應性較強,劣勢為目標識別能力較差,無法應用在背景復雜目標跟蹤中;基于區域匹配相關的目標跟蹤算法(基于邊緣匹配的平面目標跟蹤[2]),該算法以圖像目標全局信息為基礎,例如顏色、紋理等對目標進行識別與跟蹤,優勢為目標識別精度較高,劣勢為運算量大;基于特征點的目標跟蹤算法(基于特征點的KLT 實時目標跟蹤算法實現[3]),該算法選取多個奇異點,作為圖像目標特征點,對其進行提取、保存等操作,對目標進行實時跟蹤。 優勢為目標跟蹤精度較高,劣勢為目標跟蹤時效性較差;基于變形模板的目標跟蹤算法(復雜背景下基于自適應模板更新的目標跟蹤算法研究[4]),該算法以目標模板為基礎, 通過模板紋理方向變形檢索圖像中的目標,優勢為適應較為復雜的背景,劣勢為耗費時間較長;基于光流的目標跟蹤算法(基于運動預測的優化光流目標跟蹤算法[5]),該算法以目標光流場為依據,通過聚類速度相近的光流場區域,即可完成目標的提取與跟蹤,優勢為運算量較小,適合跟蹤速度較大的目標,劣勢為算法對噪聲較為敏感;基于機器學習的目標跟蹤算法(基于機器學習的單線激光雷達進行車輛識別與跟蹤方法研究[6]),算法應用機器學習理論將目標跟蹤問題轉化為目標分類問題,即分類圖像中的目標與背景,確定目標的位置,優勢為計算量較小,目標跟蹤可信度較大,劣勢為算法較容易陷入局部最優;基于貝葉斯濾波的目標跟蹤算法(用于目標跟蹤的智能群體優化濾波算法[7]),該算法應用先驗信息對目標的當前狀態進行估計,實現目標跟蹤,優勢為目標跟蹤精度較大,劣勢為隨著先驗信息的增加,算法速度逐漸減緩,無法跟蹤速度較快的目標。
在現有研究成果的基礎上,本文提出基于卡爾曼預測粒子濾波的復雜場景圖像目標跟蹤算法研究。
1 復雜場景圖像目標跟蹤算法研究
1.1 復雜場景圖像背景提取
此研究采用ViBe 算法對復雜場景圖像中背景進行提取與建模,為后續目標狀態轉移模型的構建提供便利與支撐。
復雜場景圖像背景提取步驟如下所示:
步驟一:假設復雜場景圖像背景模型表達式為
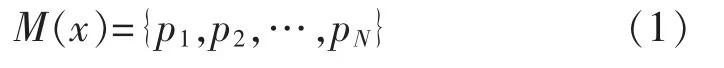
式中:M(x)表示背景模型;pN表示背景像素點,總數量為N。
依據式(1)對背景模型進行初始化,以此為基礎,從第二幀開始對圖像背景進行相應的檢測。
步驟二:對圖像中的背景與前景進行判斷。 比較背景模型M(x)與圖像像素p(x),并對相似度進行計算,計算公式為
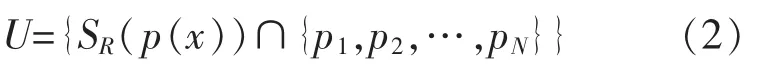
式中:U 表示待分類像素與背景模型的相似度;SR(p(x))表示以圖像某像素點為中心,以R 為半徑的球體。
則圖像背景與前景的判斷規則為

式中:Umin表示給定閾值,以此為基礎來判定圖像的背景與前景。
步驟三:在背景模型M(x)中,隨機選取一個樣本,對像素值進行替代,完成背景模型的實時更新與提取。
1.2 圖像目標狀態轉移模型構建
為了提升圖像目標跟蹤的精確性,構建模型需要與實際目標運動符合[8]。 現今應用較為廣泛的狀態轉移模型為仿射模型與自回歸模型[9]。 其中,仿射模型表達式為
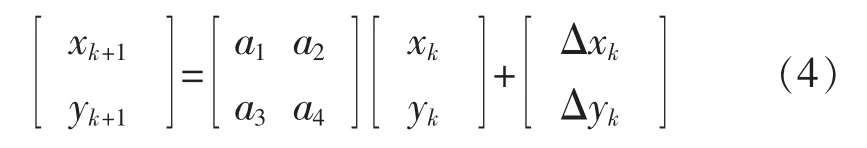
自回歸模型表達式為
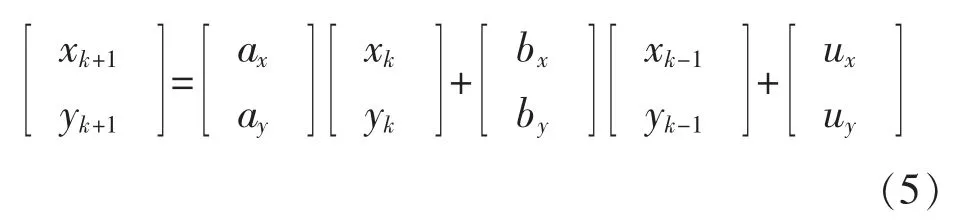
式中:ax,ay,bx,by表示線性參數;ux與uy表示高斯噪聲,并且兩者相互獨立。
1.3 圖像目標觀測模型構建
為了滿足圖像目標的跟蹤需求,此研究以目標顏色直方圖為基礎,構建圖像目標觀測模型[10]。在目標跟蹤的初始幀,需要對目標進行手動選擇,設定初始時刻目標為T0,對應的顏色直方圖為H0。 在目標跟蹤過程中,設定候選目標為T,對應的顏色直方圖為H。 目標觀測模型就是通過比較H0與H 之間的相似度,來實現目標的觀測與粒子權重的計算。
依據復雜場景圖像目標跟蹤需求,選取Bhattacharyya 距離方法對直方圖之間相似度進行計算。Bhattacharyya 距離計算公式為
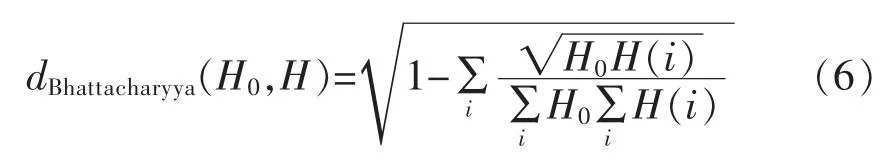
式(6)計算得到的dBhattacharyya(H0,H)數值越大,表明直方圖之間的相似程度越低,dBhattacharyya(H0,H)數值越小,表明直方圖之間的相似程度越高。
粒子權重數值計算公式為
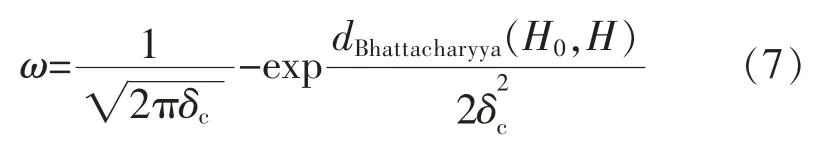
式中:ω 表示粒子權重數值;δc表示選取的固定常數,取值范圍為0~1。
通過式(7)可知,隨著dBhattacharyya(H0,H)數值的增大,粒子權重數值呈現逐漸下降趨勢,即直方圖的相似程度越低,粒子權重數值越大。
1.4 圖像目標狀態估計
基于卡爾曼預測粒子濾波估計圖像目標狀態過程實質上就是目標狀態預測及其修正過程,具體如下所示:
假設圖像目標狀態數學描述為
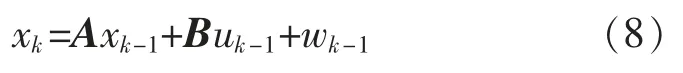
式中:xk表示當前幀的圖像目標狀態;A 與B 分別表示狀態轉移矩陣與狀態控制矩陣;xk-1表示前一幀的圖像目標狀態;uk-1表示前一幀的高斯噪聲;wk-1表示前一幀的隨機狀態噪聲。
通過構建目標觀測模型即可獲得圖像目標觀測量,表達式為

式中:zk表示圖像目標觀測量;G 表示狀態觀測矩陣;vk表示觀測噪聲。
為了方便研究的進行,設定隨機狀態噪聲與觀測噪聲相互獨立,兩者均符合正態分布,即可將其轉換為

式中:Q 與P 分別表示隨機狀態噪聲與觀測噪聲對應的協方差。 常規情況下,Q 與P 是隨著時間產生變化的,但是為了研究的便利,認定兩者均為常量。
當迭代次數為k 時,圖像目標狀態估計誤差表示為

式中:ek表示目標狀態估計誤差;表示目標狀態估計誤差修正值。
則均方誤差表達式為

當均方誤差達到最小值時,即可獲得圖像目標狀態預測方程組,定義為
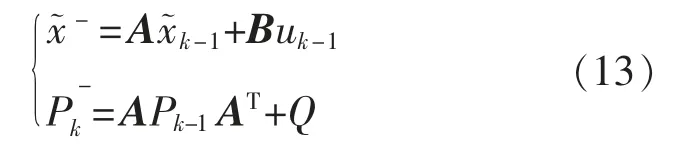
相應的圖像目標狀態修正方程組表達式為
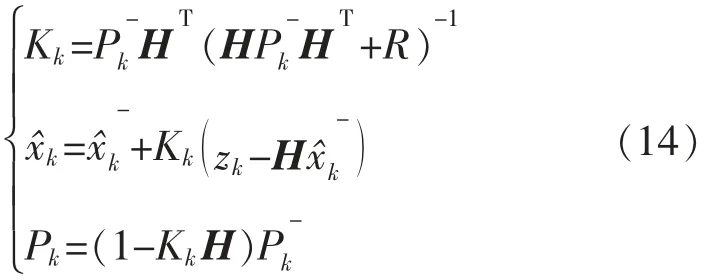
式中:Kk表示修正控制系數;Pk表示修正后的估計誤差;表示修正后的估計值。
通過上述過程完成了圖像目標狀態的精確估計,確定了每幀圖像目標的運動狀態,為后續圖像目標跟蹤的實現提供依據。
1.5 圖像目標跟蹤實現
在目標跟蹤過程中,能夠依據粒子權值估計粒子的狀態,估計公式為
式中:X 表示粒子狀態的估計結果;ωi表示粒子權重數值。
依據粒子濾波的原理,推出復雜場景圖像目標跟蹤算法,具體步驟如下所示:
步驟一:初始化。 手動選取目標模板,并計算對應直方圖。 與此同時,依據先驗分布構建初始狀態樣本集,表達式為

步驟三:計算粒子權重數值,并對其進行歸一化處理,即:

步驟四:圖像目標狀態估計,將估計結果記為xk。
步驟五:累計求和處理粒子集權重,利用均勻分布的隨機數來對粒子集進行重新采樣,生成新的粒子集。
步驟六:重復進行步驟二到步驟五,直到鎖定圖像目標的具體位置為止。
綜上所述,此研究應用卡爾曼預測粒子濾波實現了復雜場景圖像目標的跟蹤,為圖像信息應用提供充足的幫助。
2 實驗與結果分析
為了驗證提出算法的應用性能,應用引言所述7種主流算法(編號1~7)與提出算法進行實驗,通過對比分析顯示提出算法的應用性能,具體如下文所述。
2.1 圖像目標跟蹤定量分析
為了驗證提出算法是否能夠改善現有主流算法存在的問題,構建圖像目標仿真模型,表達式為
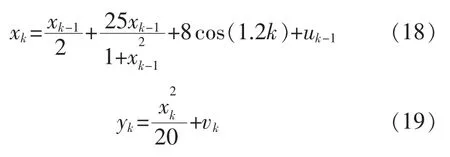
為了方便實驗的進行, 設定uk與vk均值為0,方差為10 與1。 同時,設置卡爾曼預測粒子濾波方法中粒子數量為100,閾值取值為30,迭代次數為100 次。
定量分析即選取一個評價指標對圖像目標跟蹤效果進行數值評價。 實驗以圖像目標跟蹤誤差的方差作為評價指標,其計算公式為
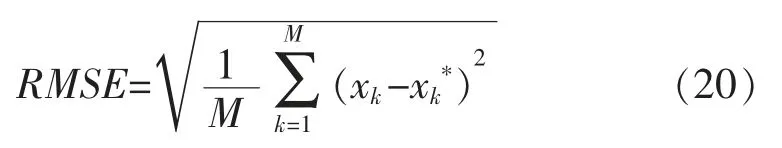
以式(20)為依據,通過實驗計算每個算法應用后的RMSE 數值,具體數據如表1 所示。
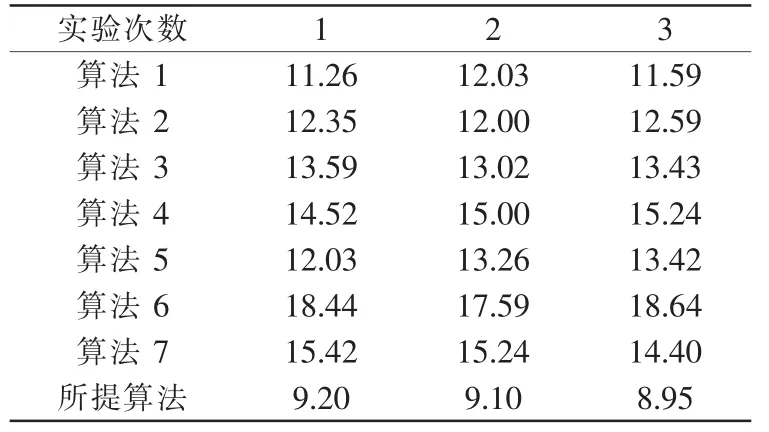
表1 RMSE 數據表Tab.1 RMSE data sheet
常規情況下,RMSE 數值越小,表明圖像目標跟蹤誤差越小,則算法的應用性能越好。 如表1 數據所示, 與7 種主流算法相比較, 提出算法的RMSE數值最小,表明提出算法的目標跟蹤誤差最小。
2.2 圖像目標跟蹤定性分析
實驗選取某段視頻為依據,將視頻中運動車輛作為實驗對象,采用7 種主流算法與本文算法對其進行跟蹤,獲得結果如圖1 所示。


圖1 圖像目標跟蹤結果示意圖Fig.1 Schematic diagram of image target tracking results
如圖1 所示,主流算法與提出算法均能夠跟蹤到圖像目標,但是7 種主流算法搜索窗口變化性較大,跟蹤窗口內包含著較多背景圖像,這非常容易造成后續目標跟蹤的失敗。 而本文算法目標跟蹤窗口較為規范,并且窗口內包含背景信息較少,更有利于后續目標的跟蹤。
2.3 復雜背景目標跟蹤結果分析
為了增加實驗結論的準確性,在不同背景復雜度下進行實驗, 驗證算法在不同場景下的適用性。以背景復雜度為自變量進行實驗,獲得圖像目標跟蹤結果如圖2 所示。
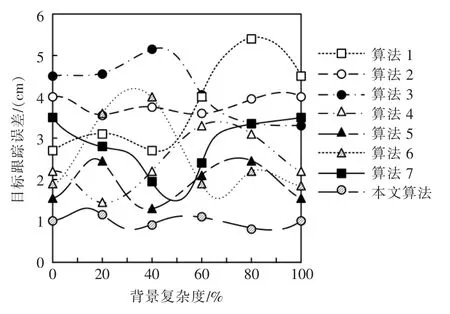
圖2 不同背景復雜度下目標跟蹤結果示意圖Fig.2 Schematic diagram of target tracking results under different background complexity
如圖2 所示,相較于7 種主流算法來看,本文算法目標跟蹤誤差較小,主要是因為本文算法在目標跟蹤前對圖像背景進行了相應的提取,可以有效降低背景在目標跟蹤過程中的影響,從而降低了目標跟蹤誤差。
2.4 圖像目標跟蹤時間分析
圖像目標跟蹤時間也是顯示算法應用效果的重要指標之一。 常規情況下,圖像目標跟蹤時間越短,表明算法應用效果更佳。 通過實驗獲得圖像目標跟蹤時間如表2 所示。
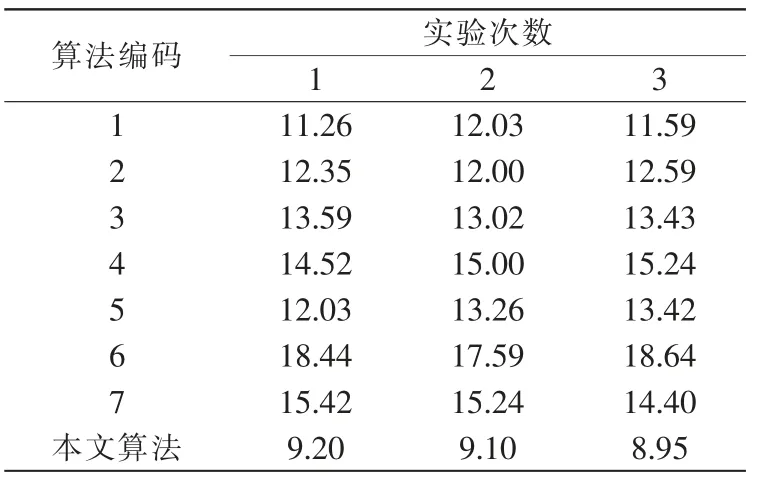
表2 圖像目標跟蹤時間數據表Tab.2 Image target tracking time data t/(ms)
如表2 數據所示,與7 種主流算法相比較,本文算法圖像目標跟蹤時間較短,能夠更及時地獲得目標跟蹤結果。
3 結語
此研究利用卡爾曼預測粒子濾波推出了新的復雜場景圖像目標跟蹤算法,通過實驗得到其平均RMSE 值為9.08,平均跟蹤時間為10.30 ms,充分證實了提出算法具備較好的應用效果,能夠滿足復雜場景圖像目標跟蹤需求,為計算機視覺發展提供助力。

