一種平面閉鏈腿式機構的尺度參數優化設計

王仙業 劉海濤 黃 田

天津大學機構理論與裝備設計教育部重點實驗室，天津，300354

0 引言

腿式機器人采用足端離散接觸地面的方式跨越障礙，對非結構化環境具有很好的適應性，因此在空間探索、戰場偵察、抗災救援等方面具有良好的應用前景[1-3]。其中，基于平面多閉環連桿機構的腿式機器人具有控制簡單、可靠性高等特點，引起了學術界的廣泛關注[4-7]。在過去的幾十年中，研究人員提出了眾多閉鏈腿式機構[8-12]，如Chebyshev機構、Klann機構、Theo Jansen機構(TJL)等。

在此類機構中，TJL可以生成與步行哺乳動物相似的足端軌跡，且該軌跡底部平緩，可有效減小行進過程中由慣性力造成的桿件與地面間的沖擊，保證了腿式機器人的平穩運動[13-14]。國內外學者圍繞TJL開展了大量研究工作[15-18]。KOMODA等[19]利用虛功原理，推導了Chebyshev、Klann和TJL三種機構的動力學模型，并在曲柄尺寸、輸入角速度和機構總質量相同的條件下，對比了三種機構的足端軌跡和能量消耗，結果表明TJL的足端軌跡底部最為平緩，且總能耗最低，更適用于腿式機器人。HAGHJOO等[20]以成年人在行走過程中踝關節相對于臀部生成的運動軌跡為目標，優化了TJL的尺度參數，據此設計了一款下肢康復訓練設備。LIU等[21]以人在上樓梯時的步態作為目標軌跡，研究了TJL的優化設計問題，并基于優化結果設計了一種爬樓梯機器人，實現了該步態軌跡的模仿。文獻[22-24]以輸入能量最小為優化目標，綜合了TJL的尺度參數。文獻[25-26]通過調節機構的桿長和機架鉸接位置，將TJL設計成一種變參數機構，從而獲得可變化的末端輸出運動。

鑒于TJL輸出的足端軌跡底部平緩、適用于腿式機器人的平穩運動，本文以TJL的足端軌跡為優化目標，研究一種平面六桿閉鏈腿式機構[27]的尺度參數優化設計問題，使其能夠很好地復現TJL輸出的運動軌跡。

1 機構描述與運動學分析

1.1 機構描述

本文研究的平面閉鏈腿式機構如圖1所示。該機構由6根連桿和7個轉動關節組成，桿AD為機架，桿ABE為原動件，桿CFG為輸出件，點G的運動軌跡為該機構的足端軌跡。利用Grübler-Kutzbach準則計算該機構的自由度:

圖1 平面閉鏈腿式機構結構簡圖

(1)

式中，n、j、fi分別為桿件數目、轉動關節數目、第i個轉動關節的自由度,n=6，j=7，fi=1。

由式(1)可知，該機構的自由度為1，因此該機構在桿ABE的驅動下具有確定的末端輸出運動。

1.2 運動學分析

如圖1所示，在點A處建立坐標系Axy，水平方向為x軸。在該坐標系下，可將Ⅱ級桿組(桿EF-CFG)中點G的位置矢量表示為

rG=rC+q1(rF-rC)+q2M(rF-rC)

(2)

式中，lCF、lCG、lFG分別為桿CF、CG和FG的長度。

由式(2)可知，為得到rG，需要先計算rC和rF。類似地，可將Ⅱ級桿組(桿BC-CD)中點C的位置矢量表示為

rC=rB+q3(rD-rB)+q4M(rD-rB)

(3)

lBD=‖rD-rB‖rB=(lAcosα，lABsinα)T

rD=(lADcosθ0，lADsinθ0)T

式中，lA、lAD、lBC、lCD分別為桿AB、AD、BC和CD的長度；lBD為點B與點D之間的距離；α為曲柄的輸入角；θ0為機架與x軸之間的固定安裝角度。

在Ⅱ級桿組(桿EF-CFG)中，點F的位置矢量為

rF=rC+q5(rE-rC)+q6M(rE-rC)

(4)

lCE=‖rE-rC‖rE=(lAEcosβ,lAEsinβ)T

式中，lAE、lBE、lEF分別為桿AE、BE和EF的長度；lCE為點C與點E之間的距離；β為桿AE與x軸之間的夾角。

將式(3)和式(4)代入式(2)，可得點G的位置矢量:

rG=ArB+BrE+CrD

(5)

A=(1-q3-q5q1+q3q5q1)I+aM+

bM2+(q4q6q2)M3

B=q5q1I+(q6q1+q5q2)M+q6q2M2

C=(q3-q3q5q1)I+cM-dM2-(q4q6q2)M3

a=q3q6q1+q3q5q2+q4q5q1-q4-q6q1-q5q2

b=q3q6q2+q4q6q1+q4q5q2-q6q2

c=q4-q3q6q1-q3q5q2-q4q5q1

d=q3q6q2+q4q6q1+q4q5q2

表1給出了文獻[27]中該機構的尺度參數，其中θ0=0°。根據式(5)，可得到不同輸入角度下機構的位形,如圖2所示。由圖2可知，該平面閉鏈腿式機構能夠近似模擬步行哺乳動物的腿部運動，但在該組尺度參數下，其軌跡底部的平緩性稍差,因此，有必要進一步研究該機構的尺度綜合問題，以得到更優的末端輸出運動軌跡。

表1 閉鏈腿式機構量綱一尺度參數

(a)α=0° (b)α=36° (c)α=72° (d)α=108°

2 尺度參數優化設計

文獻[20]給出了TJL的量綱一尺度參數(表2)。在該機構中，機架與x軸之間的固定安裝角θ0=11.6°(圖3)。由圖3可知，TJL可連接機架與足端的桿CD和桿CG(圖中綠色部分)，足端軌跡可視為由桿CD和桿CG的運動確定。注意到，在所提出的腿式機構(圖1)中存在與圖3相同的連桿，故在保證兩種機構尺度參數lCD、lCG和運動參數φ3、φ5相同的前提下，即可得到相同的輸出運動。為減少設計變量，令兩機構的桿長lCD、lCG分別相等。此外，注意到φ3由曲柄搖桿機構ABCD(圖中紅色部分)確定，故令兩機構中lAB、lBC、lAD和安裝角度θ0的取值分別相等，使得在給定相同輸入角α時，兩種機構的φ3亦相等。在上述前提下，當φ5對應相等時，兩機構的足端位置相同。

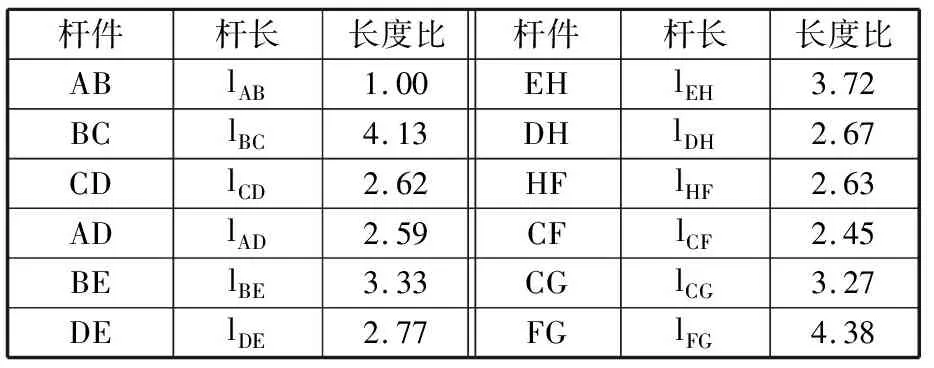
表2 TJL量綱一尺度參數

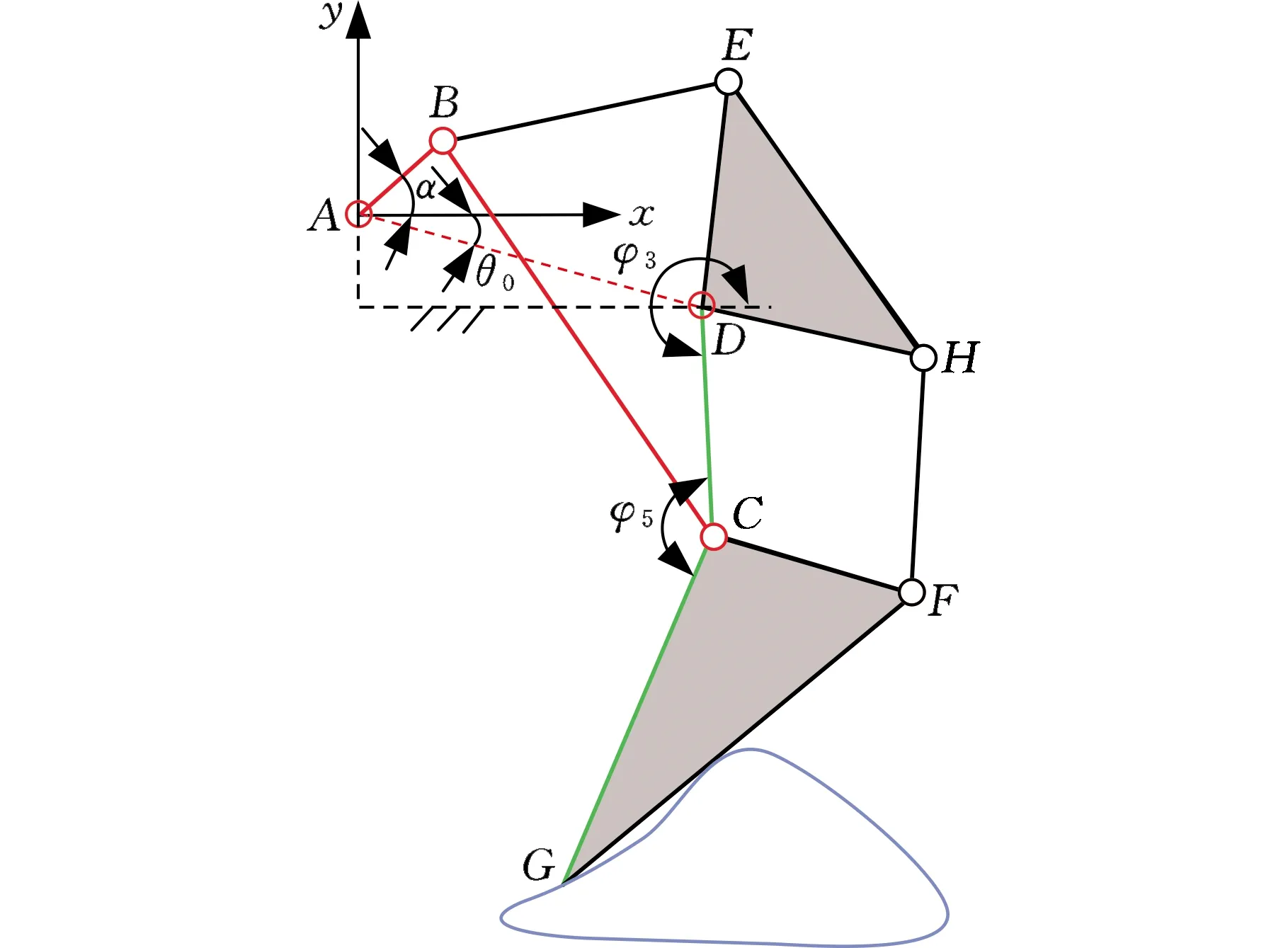
圖3 TJL結構簡圖

根據前文推導的運動學模型，可得所研究機構(圖1)中φ5的解析表達式：

(6)

TJL中φ5的求解可參見文獻[19]。為便于區分，下文將TJL的φ5記為φ′5，且其余角度亦采用相同定義方式。進一步，結合式(3)和式(5)可知，式(6)中包含lBE、lEF、lCF、lAE和lFG共5個獨立參數，將它們定義為設計向量

x=(lBE，lEF，lCF，lAE，lFG)T

(7)

2.1 目標函數與約束條件

本文的優化目標為兩機構中點G的軌跡偏差最小，基于上述分析可將其轉化為兩機構的φ5與φ′5的偏差最小，即

(8)

其中，N為一個運動周期內輸入角的離散點數目。當η取最小值時，可認為兩種機構的足端軌跡最為相近。

為了保證設計結果的可行性，依據機構尺度參數間的幾何關系來確定優化問題的約束條件。

基于上述分析，將兩機構尺度相同部分重合，得到的結果如圖4所示。結合圖2可知，在一個運動周期內，桿BE繞點B旋轉一周,故以桿BC為機架、桿BE為曲柄、桿CF為搖桿、桿EF為連桿(圖4)。根據該曲柄搖桿機構的曲柄存在條件，可得到lBE、lEF、lCF之間的約束關系：

圖4 兩種機構的結構對比

c1=lBE+lEF-lBC-lCF<0

(9)

c2=lBE-min(lEF,lBC,lCF)<0

(10)

因兩機構的lAB、lBC、lCD和lAD取值相同，故在一個運動周期內兩機構的φ2(桿AB和桿BC之間的夾角)相等，因此，φ1和φ4滿足如下約束關系：

c3=φ1+φ4=2π-φ2

(11)

式中，φ1為曲柄搖桿機構BEFC中桿BC與桿BE之間的夾角；φ4為桿AB和桿BE之間的夾角。

結合式(3)可知，φ1和φ4中僅包含lBE和lAE兩個獨立參數，故利用式(11)可得到lBE與lAE之間的隱式約束關系。類似地，在一個運動周期內兩機構的γ2(桿BC和桿CD之間的夾角)相等，則φ5和φ滿足如下約束關系：

c4=φ5+φ=2π+γ2-γ1

(12)

式中，γ1為桿CG和桿CF之間的固定角度；φ為桿CF與桿BC之間的夾角。

結合式(3)～式(5)可知，式(12)中僅包含lCF和lFG兩個獨立參數，故利用式(12)可得到設計變量lCF與lFG之間的隱式約束關系。

最終，本文所研究的平面閉鏈腿式機構優化設計問題被定義為如下單目標優化問題：

(13)

2.2 優化設計

根據等式約束c3和c4，可將設計變量進一步縮減為lBE、lEF和lCF。若采用一般的優化算法[12]，則需給定三個設計變量的取值范圍。考慮到三個設計變量與已知量lBC構成曲柄搖桿機構BEFC，且約束條件c1和c2源自該機構的曲柄存在條件，故可參考曲柄搖桿機構的優化設計方法確定三個設計變量，從而簡化優化問題的求解。

為設計該曲柄搖桿機構，首先確定其搖桿的擺角范圍。將φ視為搖桿CF的擺角，它與φ5之間滿足約束c4。注意到該約束同樣存在于TJL中，即

φ′5+φ′=2π+γ2-γ′1

(14)

其中，φ′為TJL中桿BC與桿CF′的夾角；γ′1為桿CG與桿CF′的夾角(圖4)，因此，可參考TJL確定φ的擺角范圍。圖5所示為一個運動周期內TJL中φ′的變化曲線。由圖5可知，φ′的兩個極值分別為φ′max=181.68°和φ′min=103.96°，所對應的輸入角分別為348.55°和167.94°，則擺角φ應滿足

圖5 TJL中φ′的變化曲線

Δφ=φmax-φmin=φ′max-φ′min=77.72°

(15)

其次，需要確定搖桿CF的極限位置。根據TJL中φ′的兩個極值及其所對應的輸入角，得到TJL的兩個極限位置，如圖6所示。為了保證φ5和φ′5具有相同的變化趨勢，兩機構應同時達到極限位置。由于兩機構的四桿機構ABCD相同，故需要設計的曲柄搖桿機構BEFC的機架BC可由TJL的兩個極限位置確定。進而，可確定φ的極值所對應搖桿的兩個極限位置(C1F1和C2F2)，如圖6所示。

(a)φ和φ′均為最大值

根據曲柄搖桿機構極限位置的幾何條件，即曲柄與連桿共線，可構造如下約束方程：

(16)

式中，a1、a2分別為曲柄搖桿機構BEFC兩個極限位置處點B到點F的距離。

式(16)中包含lBE、lEF、lCF和φmax四個參數。為求解式(16)，根據兩機構同時達到極限位置的條件進一步可得

‖rE1‖=‖rE2‖

(17)

i=1，2

φm1=φmaxφm2=φmax-Δφ

式中，rBi、rCi、rEi分別為兩極限位置處點B、點C和點E的位置矢量。

式(16)和式(17)提供了3個約束方程，包含4個參數。因此，當φmax給定時，便可得到lBE、lEF和lCF。進一步，根據式(8)即可定量評價兩機構足端軌跡的近似程度。為了避免曲柄搖桿機構BEFC存在奇異位形，并保證其擺角范圍，給定φmax的取值范圍為78°<φmax<180°，取離散點個數N=200，繪制η隨φmax的變化曲線，如圖7所示。由圖7可知，當φmax=168°時，η取得最小值，因此，可認為此時兩機構的足端軌跡最為接近。將φmax代入式(16)、式(17)、式(11)和式(12)，即可得到優化后機構的量綱一尺度參數(表3)。

圖7 η隨φmax的變化曲線

表3 優化后閉鏈腿式機構的量綱一尺度參數

在表1和表3兩組尺度參數下，腿式機構的φ5與TJL中φ′5的變化曲線見圖8。由圖8可知，優化后φ5的變化規律與φ′5更為接近。圖9進一步對比了兩組尺度參數下腿式機構與TJL的足端軌跡。優化后的機構與TJL具有相同的跨高h，且最大軌跡偏差小于0.26。上述結果表明，優化后閉鏈腿式機構可以很好地逼近TJL的足端軌跡。

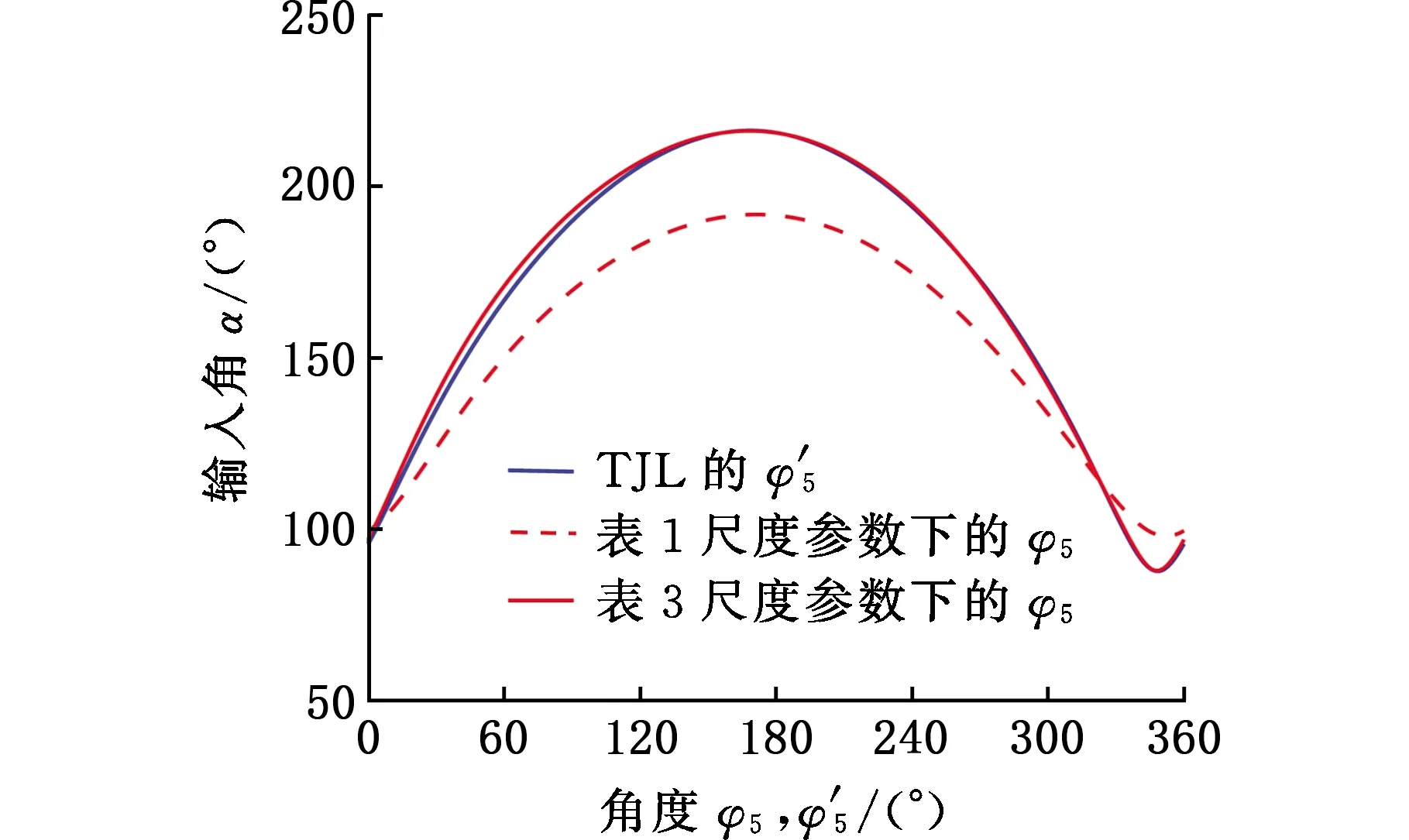
(a)角度的變化曲線

(a)足端軌跡

3 多足移動機器人樣機

利用優化后的尺度參數設計了一種多足移動機器人，其CAD模型如圖10所示。整機包括左右布置的兩個模塊，每個模塊包含一個主傳動軸和兩組前后布置的雙足步行單元，每組雙足步行單元由兩個閉鏈腿式機構、傳動齒輪組、傳動同步帶輪、曲柄軸組成。整機由安裝在中間的兩個電機驅動，并設置了電池倉來放置電池，通過同步帶輪將動力傳遞給主傳動軸；傳動齒輪組分別與主傳動軸和曲柄軸固連，主傳動軸通過齒輪傳動將動力分別傳輸到曲柄軸上；曲柄軸帶動閉鏈腿式機構的曲柄轉動，從而使閉鏈腿式機構輸出足端運動，支撐機器人在地面移動。為減小機器人質量，機身框架由碳纖維板制成，其余構件采用光敏樹脂材料3D打印成形。

(a)整體結構

雙足步行單元是機器人的行走裝置，其行走步態直接反映機器人的運動狀態。圖11為該雙足步行單元的結構示意圖，由兩個腿式機構組成，這兩個腿式機構共用一個機架，共線布置的曲柄之間相位差為180°，通過單電機驅動實現兩機構的同步運動。雙足步行單元在水平地面行走時，交替完成支撐推進和邁步跨越的動作，從而使機架向前移動。如圖11所示，支撐腿(紅色)處于支撐階段，足端支撐在點G處；擺動腿(藍色)處于擺動階段，足端在點G′處。當兩腿式機構同時接觸地面時，會有短暫的雙重支撐階段，即兩足端分別處于點O1和點O2，兩次雙重支撐之間曲柄旋轉180°，為一個行走周期。

圖11 雙足步行單元結構簡圖

為分析雙足步行單元的運動平穩性，在足端支撐的G點處建立參考坐標系Gx′y′，水平方向為x′軸；在A點處建立連體坐標系Axy，在任意瞬時位形下坐標系Axy平行于坐標系Gx′y′(圖11)。則在坐標系Gx′y′中，D點的位置矢量rGD可表示為

rGD=rD-2rG

(18)

據此，可得到雙足步行單元機架在行走過程中的運動軌跡(假設無滑動)。類似地，亦可得到采用相同結構設計的TJL雙足步行單元機架運動軌跡，如圖12所示。通過對比可知，本文設計的雙足步行單元在一個行走周期中機架上下波動幅度較小，能夠有效保證機架的運動平穩性。

圖12 行走時機架上固定點的軌跡

根據設計的多足移動機器人CAD模型，完成對電機、軸承、控制器等零件的選型，制作、裝配，得到如圖13所示的多足移動機器人實物樣機，包含機器人本體、驅動控制系統以及電池。該樣機的主要參數見表4。利用搭建的多足移動機器人開展行走實驗(圖14)，給定電機轉速為30 r/min，機器人沿直線行進，速度可達0.06 m/s。利用激光測距儀得到樣機在行走過程中主體框架與地面的距離,變化范圍為140～142.2 mm，上下波動幅度小，證明了移動的平穩性。

圖13 多足移動機器人實物樣機

表4 樣機參數

t=0 t=0.5 s t=1.0 s

4 結論

(1)在利用基本桿組法建立機構運動學模型的基礎上，以該機構與TJL的足端軌跡偏差最小為優化目標，建立了考慮尺度參數間幾何約束的單目標優化模型。通過考察機構的結構特點，利用曲柄搖桿機構的極限位置條件，有效減少了設計變量數目，并將優化設計問題簡化為一維搜索問題，進而得到優化后的機構尺度參數。優化結果表明，最大軌跡偏差小于0.26，機構可近似復現TJL的足端運動軌跡。

(2)利用優化后的機構尺度參數設計了一種多足移動機器人，并分析了雙足步行單元在一個行走周期內的運動平穩性。仿真與實驗結果表明，該雙足步行單元能夠有效保證多足移動機器人的運動平穩性，從而驗證了設計方案的可行性。