大跨度鐵路連續梁-拱組合橋拱腳應力研究

金 森，王 炎，胡曉東，曹成杰，魯 超

(1.浙江理工大學建筑工程學院，浙江 杭州 310000；2.中鐵四局集團有限公司，安徽 合肥 230041；3.浙江存真土木工程技術有限公司，浙江 杭州 310000；4.杭州地方鐵路開發有限公司，浙江 杭州 310000)

連續梁-鋼管混凝土拱組合橋承載能力高、施工便捷、對地基適應性強等優點，在高速鐵路建設中應用廣泛[1- 3]。對于鋼管混凝土連續梁拱組合橋而言，拱腳位于拱肋、主梁、墩柱、橫梁等構件集中交匯處，是受力的關鍵部位，不僅要承受拱肋傳遞的彎矩和軸力，還要承受主梁及端橫梁傳遞的縱向、橫向預應力和彎矩，受力及結構十分復雜[4- 5]，在該處易產生應力集中，從而導致拱腳部位裂縫的產生。

目前，對連續梁-拱組合橋拱腳開裂機理及應力分布規律已經有了一些探討和研究。尚軍亮、鄧風亭、李明[6- 8]等人對鋼管混凝土拱橋拱腳裂縫原因進行了分析，認為施工階段泵送混凝土壓力擠壓鋼管變形以及拱腳外包混凝土拉應力過大導致拱腳開裂。劉國光、李金凱、崔鳳坤[9- 11]等人對拱腳應力分布規律進行了研究，認為拱腳局部存在應力集中情況，主要位于鋼管混凝土拱肋與拱座連接處，該處局部應力過大引起拱腳混凝土開裂。綜上所述，目前對于拱腳開裂機理及應力分布規律已經有了一定成果，但是多數是基于成橋狀態或某一施工節點進行，而針對整個施工過程的應力研究較少。因此本文從有限元模擬和現場監測的角度針對拱腳在施工過程中的應力分布及變化規律進行分析探討，為類似工程建設提供參考。

1 工程概況

本文以一座(76+160+76)m連續梁-鋼管混凝土拱組合橋為研究對象，連續梁為預應力鋼筋混凝土結構，全長312m。主梁采用單箱雙室變高度箱形截面，跨中及邊支點處梁高4.5m，中支點處梁高9.0m，梁高按圓曲線變化。拱肋采用鋼管混凝土結構，計算跨度L=160.0m，設計矢高f=32.0m，矢跨比f/L=1∶5，主拱采用等高啞鈴型截面，截面高度為3000mm，由上、下2個單圓鋼管和綴板焊接而成。上、下單圓鋼管直徑為1000mm，壁厚為16mm。二榀拱肋之間共設9道橫撐，橫撐均采用空間桁架撐，各橫撐由4根Φ450mm×12mm主鋼管和32根Φ250mm×10mm連接鋼管組成。全橋共設15組雙吊桿，每組吊桿順橋向間距9m。主橋橋型布置圖如圖1所示。

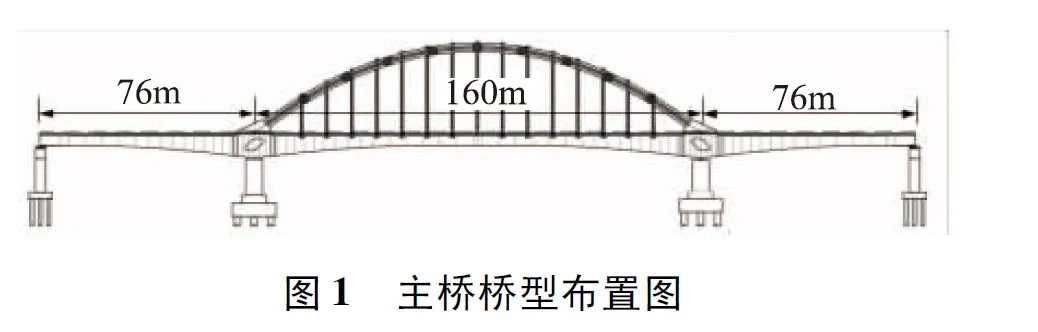
主橋的施工方法為“先梁后拱”[12]，主要的施工步驟為：①利用掛籃懸臂澆筑主梁；②合攏吊架配合進行邊跨和中跨合攏；③搭設橋面支架，利用支架進行拱肋的分段拼裝；④拆除橋面支架，依次進行拱肋上下弦管及綴板內混凝土的灌注；⑤吊桿進行初張拉；⑥橋面二期恒載的鋪設；⑦吊桿二次調索至設計索力。

2 拱腳應力監測點布置

選定左右側拱座背面1-a～1-b和1-a’～1-b’、上下弦管與拱座交界處2-a～2-d和2-a’～2-d’、上下弦管端部3-a～3-d和3-a’～3-d’共20個位置為應力監測點，左右側拱座的應力監測點對稱布置，如圖2所示，通過埋入式智能弦式應變計來監測施工過程中的拱腳局部應力，并根據拱腳混凝土的傳力特點，將弦式應變計沿主筋方向布置，如圖3所示。

3 有限元分析模型

在連續梁-鋼管混凝土拱組合橋中，拱腳位于結構交匯處，受力及構造十分復雜。在全橋模型中，拱腳結點用桿系單元進行了簡化處理，從而忽略了拱腳的具體構造。顯然，簡化處理下的結點受力不能充分反映拱腳的具體受力情況，需要采用更精確的局部模擬分析，才能準確地求解拱腳處的應力分布規律[13- 14]。因此，建立多尺度有限元模型進行拱腳受力特性分析具有必要性，本文先通過建立全橋模型，并提取出各施工階段的局部等效邊界荷載，再將該荷載施加到局部有限元模型中進行拱腳受力特性分析。

3.1 全橋有限元模型建立

全橋模型采用有限元分析軟件Midas/Civil建立，如圖4所示。在模型中主梁、拱肋及橫撐采用梁單元模擬，吊桿采用只受拉桁架單元模擬，拱肋截面采用施工階段聯合截面建立，結構考慮縱向預應力荷載及收縮徐變，根據實際施工工況進行施工階段模擬[15]。模型中x軸為順橋向，y軸為橫橋向，z軸為豎橋向。

通過有限元模擬計算，得到各個施工工況的等效邊界荷載，見表1。其中，軸力N以受拉為正；剪力Q以順指針方向旋轉為正；彎矩M以下側受拉為正。

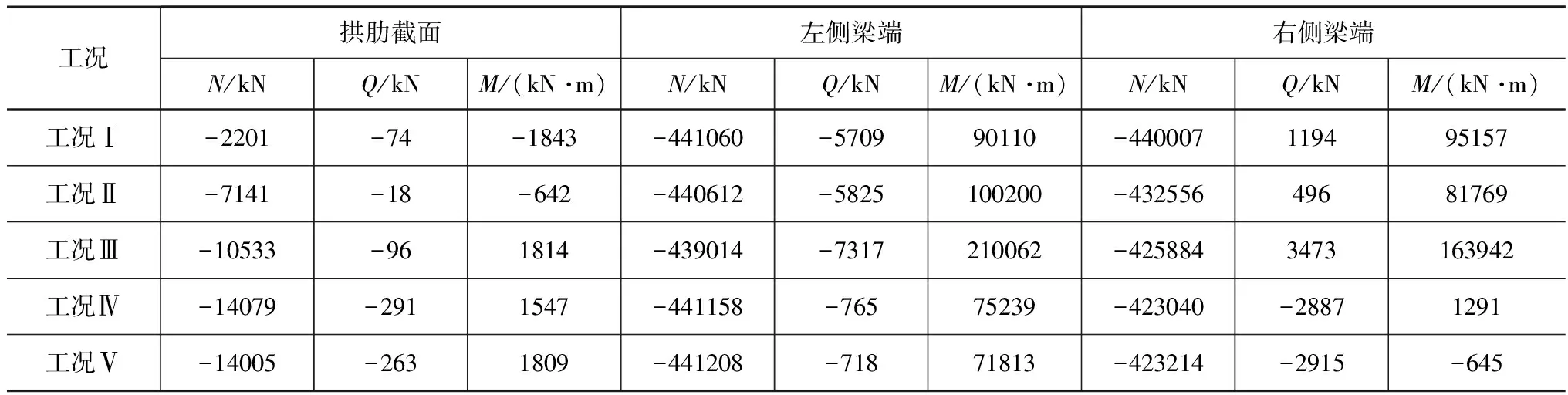
表1 截斷處等效邊界荷載結果

3.2 拱腳實體模型建立

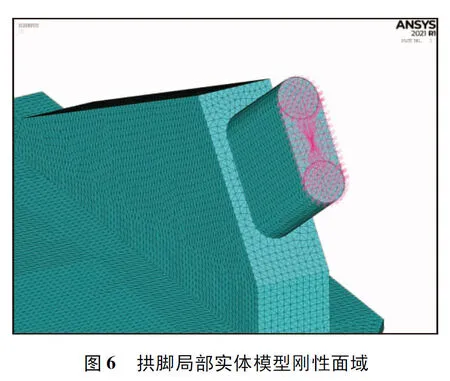
拱腳實體模型采用ANSYS建立，如圖5所示[16]。在建立模型時假定拱肋鋼管與填充混凝土協調變形，不考慮材料非線性，以及拱肋與拱腳混凝土的相對滑移。實體模型采用SOLID45單元模擬，拱肋、拱座及主梁采用共節點方式進行耦合。混凝土及拱肋鋼管材質分別采用C55混凝土和Q325D鋼材，材料參數通過TB 10092—2017《鐵路橋涵混凝土結構設計規范》選取[17]。模型的邊界內力加載通過剛性面法來實現，如圖6所示[18]。即通過在截斷面幾何中心處建立mass21質量點單元并施加截斷面邊界荷載，見表1，然后采用rbe3剛性連接單元將質量點單元與截斷面的節點連接，從而實現荷載的分配。模型中z軸為順橋向，x軸為橫橋向，y軸為豎橋向。在建立拱腳局部模型時，根據實際的支座位置在實體模型底部進行約束，其中，中支座約束z和x方向，邊支座約束z向，主梁端部截面約束平面外的平動和平面內的轉動。

4 有限元計算結果與實測值比較

4.1 拱腳局部模型計算結果

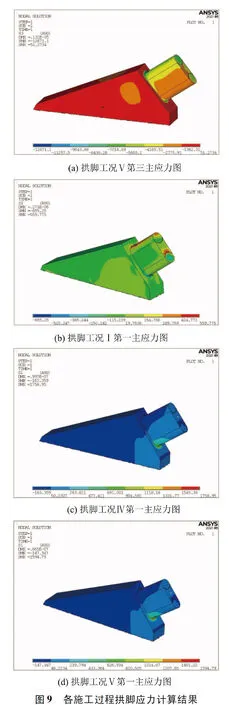
拱座及拱肋材料為C55混凝土，屬于實體脆性結構，根據第一、第二強度理論，采用第一主應力進行最不利拉應力分析，采用第三主應力進行最不利壓應力分析。根據有限元計算結果，各監測點施工過程中的理論結果如圖7所示，得到拱座的應力分布情況為拱肋與拱座交界處為最不利位置，拱座背面次之，上下弦管端部的應力值最小。其中最大的拉壓應力均出現拱肋與拱座交界處，變化規律如圖8所示。

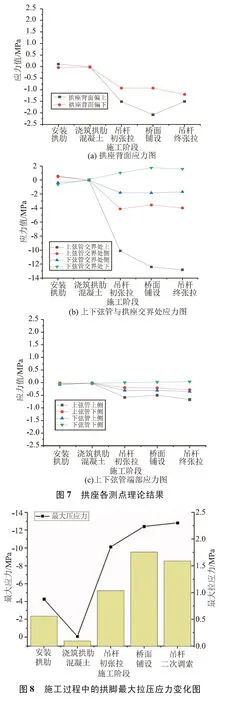
經分析，拱座混凝土在施工過程中基本處于受壓狀態，在工況Ⅲ及后續工況時，拱座混凝土壓應力顯著增大，在工況Ⅴ時壓應力達到最大值-12.671MPa，如圖9(a)所示；拱座混凝土最大拉應力變化情況為：在工況Ⅰ時，最大拉應力為拱肋上弦管交匯點，最大拉應力為0.559MPa，如圖9(b)所示。隨著吊桿張拉、橋面鋪設等工況的進行，拱肋豎向荷載增大，最大拉應力由上弦管交匯點轉變為下弦管交匯點，在工況Ⅳ時，下弦管交匯點最大拉應力為1.758MPa，如圖9(c)所示。二次調索工況時，為達到設計索力，而對吊桿內力進行了釋放，導致拱肋豎向荷載較少，引起下弦管拉應力降低，如圖9(d)所示，由此可以得到下弦管受拉程度與拱肋豎向荷載大小呈正相關。

4.2 實測值與理論值對比分析

將現場測值列于表2，分析實測數據可知，拱座整體受壓，最大拉應力為2-d測點，最大壓應力為2-a測點；由第二組實測數據圖10(b)可知，在工況Ⅰ時2-a受拉、2-d受壓，隨著施工工況的進行，逐漸轉變成2-a受壓、2-d受拉；通過分析第一組圖10(a)和第三組圖10(b)實測數據可知，第三組實測位置即上下弦管端部為應力最小位置；在工況Ⅲ時，拱座整體拉壓應力發生較大變化。應力變化規律與有限元模擬結果一致，驗證了有限元模擬結果的可靠性。

表2 現場實測數據值 單位：MPa

5 結語

以某大跨度連續梁-鋼管混凝土拱組合橋為研究對象，通過Midas/civil和Ansys聯合仿真，并結合現場實測對拱腳在各施工階段的受力特性進行分析，結果表明：

(1)在施工期間，拱腳基本處于受壓狀態，整體受力合理。

(2)在施工過程中，拱座最不利受力位置為拱肋與拱座交匯處，建議在此處加強構造措施和優化配筋，確保結構受力的合理性。

(3)拱肋下弦管拉應力與拱肋豎向荷載大小呈正相關，為防止拱座在施工時由于下弦管拉應力過大導致開裂，在鋪設橋面系和張拉吊桿時，應注意控制橋面系荷載值和吊桿張拉力的大小。

(4)實測值與有限元模擬結果相接近，表明有限元模擬方法可靠，可用于驗算設計。