初中數學“命題、定理、證明”教學研究

李庾南 劉東升

摘要：七年級平面幾何入門階段，關于“命題、定理、證明”的教學研究往往是各級教研活動的一個薄弱點。如何將這部分內容中比較抽象的數學概念形象生動地呈現出來？怎樣把這些零散的概念或知識點串聯起來？可以從理解課標、理解教材出發，梳理出思維導圖，精選典型實例改編成“問題串”，驅動結構化認知的生成。

關鍵詞：“命題、定理、證明”;教學研究;結構化認知

本文系江蘇省教育科學“十四五”規劃課題“高質量發展視域下‘三學’立人的實踐研究”（編號：TSXM/2021/06）的階段性研究成果。課題主持人：李庾南、祁國斌。七年級平面幾何入門階段，關于“命題、定理、證明”的教學研究往往是各級教研活動的一個薄弱點。從一些隨堂課的觀課情況來看，有些教師在教學中確實存在“一個定義、三項注意、大量練習”（章建躍語）的問題。如何將這部分內容中比較抽象的數學概念形象生動地呈現出來？怎樣把零散的概念、知識點串聯起來？最近，我們在集體備課時，對這些問題做了較為深入的教學研討。

一、知識梳理與解讀

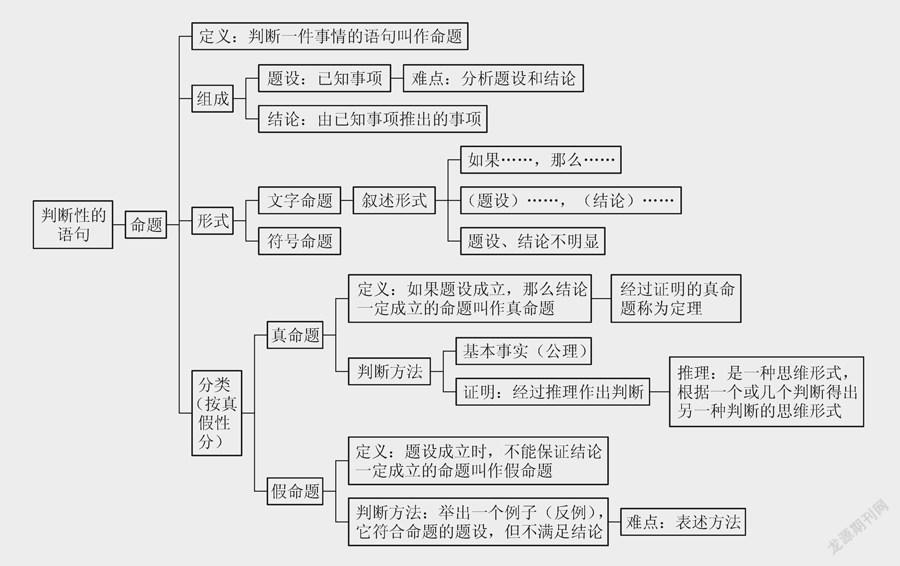
我們首先對人教版初中數學七年級下冊 “5.3.2命題、定理、證明”的內容做了知識梳理與解讀，預設出所要形成的知識網絡（如下頁圖1所示）。

根據《義務教育數學課程標準（2022年版）》的要求，七年級新授階段，只要求學生“通過具體實例，了解定義、命題、定理、推論的意義。結合具體實例，會區分命題的條件和結論”。考慮到幾何內容分布在不同分冊教材中，對于命題的相關知識，人教版教材也是分散安排的，教學時要注意把握七年級的教學要求，特別是“結合具體實例”幫助學生了解相關概念。

二、教學設計

（一）生成“命題”概念

問題1研究下列語句的特點，側重分析它們是否是對某個數學概念或性質的判斷。

（1）如果兩個角互補，那么它們的和為180°;

（2）作∠AOB的平分線OC;

（3）a的相反數為-a嗎？

（4）∠AOB=90°，AO⊥BO;

（5）直角都相等;

（6）相等的角都是直角。

在學生分析上述語句的特點之后，抽象概括出命題的概念及構成（命題由題設和結論兩部分組成，題設是已知事項，結論是由已知事項推出的事項）。需要講解清楚的是，命題常寫成“如果……那么……”的形式，“如果”后接的是題設，“那么”后接的是結論。在此基礎上，繼續安排一組習題，讓學生判斷這些語句是不是命題，如果是命題，則判斷命題是否正確。即讓學生“回到命題的定義”去解題，將命題的概念具體化，通過恰當、必要的追問，讓學生知道命題中需要有“一件事情”和“判斷”等關鍵信息。

（二）辨析命題的“題設”和“結論”

問題2分析下列命題的題設和結論。

（1）如果兩個角互為補角，那么這兩個角的和等于180°;

（2）如果x=0，那么xy=0;

（3）大于90°而小于180°的角是鈍角;

（4）直角都相等;

（5）同角的余角相等;

（6）內錯角相等。

前兩個小問，學生容易分析出“如果”后面是題設，“那么”后面是結論;后四個小問，可以引導學生先將它們改寫成“如果……那么……”的形式，再來辨析它們的題設和結論。講評這個問題時，教師還要注意以下兩個方面：一是讓學生知道命題既有文字命題的形式，也可以用符號語言來表示，如第二小問;二是幫助學生根據已有的經驗，學會判斷命題的正確性。進一步地，按命題的真假性，可以將其分為真命題和假命題兩類。

（三）了解“推理”“證明”和“定理”

問題3判斷命題“垂直于同一直線的兩直線平行”的真假，并說明理由。

在訓練命題真假性判定的基礎上，讓學生了解推理和證明的意義，體會推理、證明的基本步驟，并初步學習數學文字語言與圖形符號語言的互化，為以后證明文字命題奠基。在推理過程中運用到的依據，一般有定義、公理、基本事實、定理、推論等。這里，可讓學生了解定理的概念，即經過推理證實其為真并且可以它為依據推證其他命題的真命題叫作定理，定理是重要的真命題。順便可讓學生回顧已經學過的一些定理、公理（或基本事實）。

問題4判斷下列命題的真假，如果是真命題，說明理由;如果是假命題，舉反例說明。

（1）如果兩個角互余，那么這兩個角都是不大于45°的角;

（2）如果a+b>0，那么a>0，b>0。

教學時要讓學生知道，真命題無一例外總是正確的，而假命題則不能保證總是正確的，只要能找到一個反例，就可以說明某個命題是假命題，從而幫助學生正確理解命題的真假性。

（四）完善結構化板書

問題5本課我們學到了哪些數學概念，舉例說說你對它們的理解。

問題6證明“兩直線平行，同旁內角的平分線互相垂直”這道文字命題時，你覺得要分哪幾步？

問題5是開放性的，學生可結合本課所學，先小組內交流，再全班匯報，教師進行必要的追問，并完善、形成本課的結構化板書（類似圖1）。對于問題6中文字命題的證明，要讓學生知道應先分析命題的題設和結論，然后將文字命題的題設、結論分別轉化為圖形語言和符號的形式，再進一步去分析證明思路，書寫推理過程。具體的解答過程，則可以作為課后作業安排學生完成。

三、教學立意的進一步闡釋

在研究某個課時的教學時，首先要查閱國家頒布的學科課程標準。課程標準一般從整個學段（如初中為7—9年級）提出某個知識點的教學要求，我們可以在此基礎上厘清本課時教學的具體要求。“命題、定理、證明”在初中學段只要求“結合具體實例了解”，那么本課時就要注意放低起點，精心挑選恰當的實例來幫助學生理解這三個概念。比如，在生成“命題”概念時，問題1中（1）是對“和”作出判斷，（2）是祈使句但不是判斷句，（3）是疑問句但未作出判斷，（6）是判斷但判斷不正確。由此，學生可以明確，命題中需要有“一件事情”和“判斷”等關鍵信息，從而將抽象的“命題”概念具體化。

特別要指出的是，有些教輔資料隨意編寫一些生活中的語句，如“今天的天氣真好”“這本書你看完了嗎”等，讓學生辨析它們是不是命題。我們認為，這些沒有數學味的語句屬于“無趣題”，對學生理解數學命題的概念意義不大，不宜出現在數學命題的教與學中。

人教版初中數學教材在“命題、定理、證明”這一課時的內容安排上，以大段文字的講解為主，比較抽象，我們在研讀教材的基礎上，先將本課中一些概念之間的關系梳理成思維導圖，再選編幾組“問題串”，分別在這些“問題串”的驅動之下依次引出命題、定理和證明的概念，并漸次生成結構化板書，使得教學環節分明、層層遞進、漸次生長。這也是教師需要加強修煉的基于教材的加工轉化能力。