中考數學中的基礎題與能力題例談

譚麗春，周怡杉

中考數學中的基礎題與能力題例談

譚麗春，周怡杉

（南寧師范大學，廣西南寧530100）

本文通過對中考數學中的基礎題與能力題的思考，結合數學知識、數學技能、數學能力三者的關系，分析數學基礎題和數學能力題的題型特點、解題方法及其教學策略，以期能夠從教學實踐方面對數學能力的培養有所啟示。

四基；數學能力；基礎題；能力題

義務教育階段的數學課程總目標是：通過義務教育階段的數學學習，學生能夠掌握社會生活和進一步發展所需要的數學“四基”，增強發現問題和提出問題、分析問題和解決問題的能力。從中可以看出：《義務教育數學新課程標準修訂（2011年版）》明確地將“發展‘四基’、培養和發展學生的數學能力”作為數學教育的目的之一。

要使新的課程改革得到真正的落實，教育評價的研究必須先行。為了體現“四基”與能力的考查，在中考數學中，數學基礎題和數學能力題是基于“四基”與能力立意的命題方向的具體體現。中考是衡量學生是否達到畢業標準的重要依據，試卷結構必須科學，要綜合考慮試卷的難度、信度、效度、可信度。所以中考數學試卷的命制既要通過基礎題考查學生在數學學科知識與技能方面的水平，又要通過能力題考查學生的數學能力。下面本文將通過具體例子談談中考數學中數學基礎題和數學能力題的常見題型。

一、中考數學中常見的基礎題題型

數學基礎題以考查學生數學基本知識和基本技能的理解和掌握為目的，寓數學思想方法和數學活動經驗于問題情景之中。這類題目往往具有以下特點：①題目包含的信息容量小，一般包含1-2個數學命題和對象；②知識結構單一，要求能夠對數學知識達到理解、識記的程度；③問題往往由一些基本的數學事實性知識（如定義、定理、公式、特定的證明等）和數學活動經驗即可解決。

基礎題首先考查的是數學課程標準中最基礎、最核心的內容，即所有學生在學習數學和應用數學解決問題的過程中最重要、必須掌握的核心觀念、核心思想、基本概念和常用技能。數學基礎題注重考查“四基”，結合“四基”的特點可以將中考數學中常見的基礎題題型分為以下幾種：

（一）知識再認型

“知識再認”指的是對數學知識的再認與回憶。知識再認型題目考查的是學生通過問題情景的關聯性，能否提取在學習過程中理解、記憶并系統化了的數學知識，即考查的是學生對基本知識的理解、掌握以及重組，同時也是檢驗學生數學知識掌握程度的重要途徑。

例1 (2019年廣西南寧中考)2019年6月6日，南寧市地鐵3號線舉行通車儀式，預計地鐵3號線開通后日均客流量為700000人次，其中數據700000用記數法表示為（）

A.70×104B.7×105C.7×106D.0.7×106

（二）基本演算型

數與代數是初中數學課程的重要組成部分，數與代數部分包括數與式、方程與不等式、函數。而數的運算始終貫穿數與代數學習的全過程，所以學生的運算水平在數學學習中至關重要，也是中考考查內容之一。

例2 (2019年廣西南寧中考)下列運算正確的是（）。

基本演算型的題目要求學生能夠根據法則和運算律正確地進行運算，更高層次的要求是學生能夠根據算式特點巧妙地選擇合適的公式簡化計算。基本演算型的題目是考查學生運算水平的重要途徑。

（三）基本操作型

“空間觀念”是《義務教育數學新課程標準修訂（2011年版）》提出的十個核心概念之一，文中并沒有對“空間觀念”的內涵作具體的描述，但從四個方面對它的特征進行了描述，其中包括能夠描述圖形的運動和變化、依據語言的描述畫出圖形。所以能夠依據圖形的結構、關系，對圖形進行分析、操作也是中考數學的考查內容之一。

例3 如圖，在△中，=，∠=40°，觀察圖中尺規作圖的痕跡，可知∠的度數為（）。

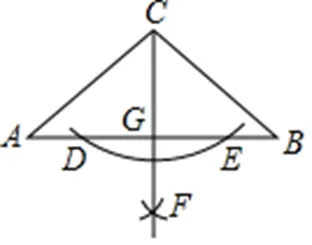
（四）基本方法應用型

數學思想和數學方法以數學基本知識和基本技能為載體，是數學學習和教學的精髓。以知識為載體的數學思想與方法是意識形態的，看不見、摸不著，所以對于數學思想和數學方法的考查，要以試題為媒介。

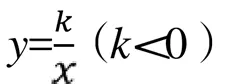
以上是中考數學中常見的基礎題類型，對于基礎題，直接運用基本知識技能、思想方法以及基本經驗即可解決。基礎題在中考數學試卷中比重較大，基礎題重在考查“四基”，在數學學習中，學生要加深對知識的理解，要梳理知識的脈絡，牢固掌握數學知識，不能死記硬背，理清新知識與舊知識的區別與聯系，將新知識重組建構，形成完整的知識體系。教師在數學教學過程中要反復滲透數學思想，引導學生總結、歸納數學方法。總之，一個好的數學教學，是能夠把數學知識、數學方法、數學思想、數學思維融為一體的教學。

二、中考數學中常見的能力題題型

綜合近幾年的試題來看，中考數學中的能力題往往具有以下特點：①題目包含的信息容量大，一般包含多個數學命題和數學對象，從而能夠實現不同數學知識和數學思想方法的融合；②知識的綜合性和層次性增強，要求對數學知識的理解水平能夠達到系統化和具體化，重建或調整認知結構達到知識的融會貫通，并使知識得到廣泛遷移的程度；③問題的探索性和創造性增強，問題解決的思路往往會有多個方向，需要依據數學知識的理解和數學思維對解題方案進行及時控制和調整，在一定程度上能夠檢測學生的數學能力。

數學能力是在獲得數學知識和數學技能的基礎上，通過廣泛遷移，不斷概括化、系統化，即類化而實現的。數學能力是數學技能的進一步沉淀與升華。數學基礎題的訓練能夠為學生搭建牢固的基礎，數學能力題可以使學生在學習上有進一步的突破。數學能力題綜合性強，解法靈活多變，從近幾年的中考數學來看，中考數學中常見的能力題題型有以下幾種：

（一）動態型問題

動態幾何問題常見的解決方法是以靜代動，常常通過對問題中的某些點（常取特殊位置）的動態變化查找動點的軌跡，大膽預測動態圖的形狀，然后再進行邏輯推理的證明。以圖形的動態變化考查學生對點、線、面之間的位置關系等基礎知識的掌握及一定的作圖能力和幾何直觀能力，要求學生熟練掌握圖形的相對位置關系。

（二）存在性問題

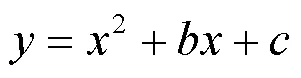
（1）求該拋物線的函數解析式。

幾何法要求學生能夠畫出所有符合條件的平行四邊形，對學生的圖形感知能力要求很高。而且本題以二次函數為背景，而平面直角坐標系作為數與形的橋梁，在此前提下，顯然本題的解題思路采用代數法更簡便。

（三）新定義題

新定義題要求學生能夠在現有知識的基礎上，經歷類比、遷移、概括、抽象的過程理解一個新定義，并能夠用現有知識和語言重新表述新定義的內涵。

這個題目是常見的新定義題型，最關鍵的是要理解a×b的運算法則。本題目經歷了從舊知到新知、從新知到實際應用的兩次遷移，充分考查了學生的類比遷移能力，學生需經歷嘗試、探索、歸納、概括、抽象的完整思維過程，充分體現了學生的數學探究能力。此類題要求學生具備扎實的基礎知識、理解閱讀能力，從而能夠根據舊知識理解新定義，并運用新定義解決數學問題。

（四）閱讀理解題

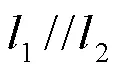
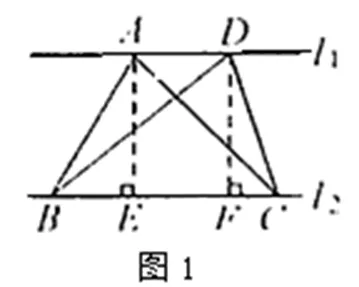
∴AE=DF。

【類比探究】問題①，如圖2，在正方形ABCD的右側作等腰△，=，AD=4，連接AE，求△的面積。

解：過點E作EF⊥CD于點F，連接AF。

請將余下的求解步驟補充完整。

【拓展應用】問題②，如圖3，在正方形ABCD的右側作正方形CEFG，點B、C、E在同一直線上，AD=4，連接BD、BF、DF，直接寫出△的面積。

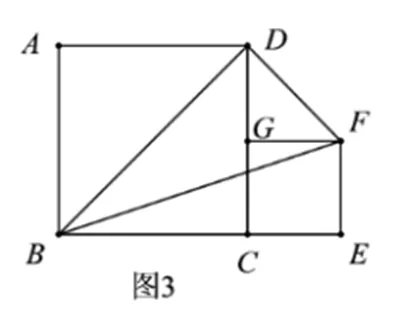
閱讀理解題是給定一段閱讀材料，要求學生通過對閱讀材料的理解、加工、整理，提取出其中蘊含的數學知識要點，領會其中的數學方法，并能夠類比遷移，應用到新的問題情景中。這類題目主要考查學生的閱讀理解能力和信息提取能力。

三、結論

中考作為學生學業成績測量的一種手段，既是對數學知識、數學技能方面的考查，也是對學生在學習過程中表現出來的各種數學能力的程度、水平的測量。在數學學科中，數學知識與技能是顯性的教學目標，數學能力目標則是以內隱的形式蘊含其中的教學目標。所以在數學教學過程中，教師要鉆研教材，挖掘蘊含的數學能力，通過學科總目標和課時目標中的知識技能、數學思考、問題解決、情感態度等滲透對學生數學能力的培養。

（一）注重數學知識的聯系

在教學過程中，教師要整體、全局地把握教材，了解知識的背景、發展過程，引導學生梳理知識脈絡，注重對知識體系的建構和對知識內容的掌握。教師要注重知識的內在聯系，挖掘教材中內在的數學思想方法。扎實的知識基礎是解決基礎題的關鍵，也是數學能力發展的前提條件。

（二）抓住數學能力培養的關鍵期

在教學中，教師應采用“探究式”的教學方法，關注學生的學習過程，抓住數學能力培養的關鍵期，在探索數學知識的過程中培養學生的數學能力。

（三）培養學生檢查自己思維的習慣

在學習和教學過程中，教師要注重培養學生檢查自己數學思維、解題思維的習慣，認識自己的優勢和不足，促進數學能力和數學思維的發展，從而在解題過程中能夠通過對知識的理解，設計并調控解題方案。

總之，在教學過程中，教師應把握好“四基”與數學能力的關系，訓練基礎題，夯實基礎知識和培養數學技能，循序漸進由簡到繁；在面對難題時，鼓勵學生大膽嘗試，在試誤過程中發展學生的數學思維，促進能力題的解決，發展學生的數學能力。

[1] 馬云鵬.數學教育測量與評價[M].北京:北京師范大學出版社,2009.

[2] 曹才翰,章建躍.數學教育心理學(第3版)[M].北京:北京師范大學出版社,2018.

G622

A

1002-7661(2022)12-0135-03