WSN中基于改進粒子群算法的覆蓋漏洞檢測

宋 娜 馮夢清

(鄭州工業應用技術學院信息工程學院 河南 鄭州 451150)

0 引 言

目前，無線傳感器網絡(Wireless Sensor Network,WSN)使用越來越廣泛，如環境檢測、智能家居和現代農業等，這些場合需要無線傳感器網絡覆蓋的完整性[1-2]。但是傳感器在初始化階段往往隨機布放在所監控區域中、節點能量消耗不均勻，最終漏洞出現使得覆蓋范圍有限，導致整個網絡失效。當前對于無線傳感器網絡覆蓋漏洞檢測方法主要有：① 跳數算法(Hop Algorithm,HA)，主要是通過節點到鄰居的通信鏈路是否連通來判斷漏洞邊界節點，對跳數較大的節點效果比較好[3]，但是由于跳數需要遍歷性，所以時間開銷較大；② 鄰域拓撲算法(Neighborhood Topological Algorithm, NTA)是指如果某個節點的密度低于所有鄰居節點密度的平均值，則表示該節點為覆蓋漏洞邊界節點[4]，但是這種方法對于密集型網絡的效果并不理想，會出現誤判現象；③ 幾何分布式算法(Geometry Distributed Algorithm,GDA)，該算法首先需要計算傳感器節點及其相鄰兩節點形成的三角形的外接圓的半徑和圓心，然后根據計算幾何理論判斷節點是否為覆蓋漏洞的邊界節點[5]；④ Voronoi圖算法(Voronoi Graph Algorithms,VGA)是指若節點的監測范圍與當前節點到Voronoi圖頂點的長度小于設置的閾值，判斷當前節點在覆蓋漏洞邊界上[6]；⑤ 循環分布式算法(Circular Distributed Algorithms,CDA)主要是根據循環覆蓋和相鄰節點的信息構建關系表，然后通過查詢此表來檢測覆蓋漏洞的位置[7]；⑥ 粒子群算法(Particle Swarm Optimization,PSO)，該算法在進行無線傳感器網絡覆蓋漏洞檢測時，由于后期處理容易陷入局部最優，無法獲得真正的覆蓋漏洞邊界[8]。上述算法在檢測覆蓋漏洞的位置信息時，對覆蓋漏洞的面積僅僅通過近似三角形進行計算，這導致了計算精度比較低的問題。為此，本文給出一種無線傳感器網絡基于改進粒子群算法的覆蓋漏洞檢測方法(后文簡稱為IPSO)，該方法對覆蓋區域進行單元格劃分，通過比較單元格的坐標位置和放置在該單元中的每個傳感器節點位置來分析是否有覆蓋漏洞以及覆蓋漏洞邊界，改進粒子群主要進行粒子的適應度函數值與自身當前最佳值比較，以便獲得最優檢測效果，最后對覆蓋漏洞檢測相關內容進行仿真，驗證了所給方案的合理性。

1 無線傳感器網絡覆蓋漏洞判定

1.1 覆蓋漏洞檢測

無線傳感器網絡監測區域中若有未被任何傳感器節點所覆蓋的范圍，則該范圍稱為覆蓋漏洞。覆蓋漏洞檢測需要對覆蓋區域劃分成若干個單元格，對每個單元格進行相同的統計操作，每個單元格中包含若干傳感器節點，如圖1所示采取了4個單元格。

圖1 單元格

對于每4個單元格共用頂點采用Delaunay三角剖分法，由于Delaunay三角形的外接圓內不包含其他節點[9]，每一個Delaunay三角形的外接圓被稱為其對應的空外接圓，三角形頂點分別選擇離共用頂點較近的三個傳感器節點，這樣構成的Delaunay三角形邊長分別為a、b和c，此三角形的空外接圓半徑rc計算式表示為：

(1)

當形成的一個三角形的空外接圓半徑rc大于傳感器節點的感知半徑r，該三角形空外接圓圓心Oc到該三角形的三個頂點的距離大于r，此時該三角形空外接圓圓心Oc都沒有被三個傳感器節點所覆蓋，則說明無線傳感器網絡可能產生覆蓋漏洞。

1.2 覆蓋漏洞位置

利用無線傳感器網絡每個節點都能夠收、發信息特性，這樣每個節點都能獲得周圍鄰居節點的位置信息，利用位置信息構建Delaunay三角外接圓圓心位置，圓心坐標(x,y)表示為：

(2)

式中：x和y為外接圓圓心的坐標，xi和yi為構成該傳感器網絡中三個節點的位置坐標，i=1,2,3。當外接圓圓心到Delaunay三角形任何一個節點的距離大于傳感器的感知半徑時，即得出覆蓋漏洞的中心位置在(x,y)處。

1.3 覆蓋漏洞面積計算

覆蓋漏洞檢測方案通過選擇最近的傳感器節點到單元格頂點的坐標來計算漏洞面積，選擇策略是通過比較單元格的坐標位置和放置在該單元中的每個傳感器節點位置完成。在選擇所需的傳感器節點數后，覆蓋漏洞檢測算法選擇最近的傳感器節點作為單元格的頭節點。頭節點有兩個功能：從其他節點收集數據，并根據選定的路由協議對其進行分類；使用三角測量法計算漏洞面積[10-11]。

覆蓋漏洞檢測方案是通過比較選擇的傳感器節點與每個單元邊緣位置點的最大傳輸范圍，如果所選傳感器節點的傳輸范圍在單元格的邊緣內，則沒有覆蓋漏洞；反之，如果在單元格的邊緣之外，則肯定存在覆蓋漏洞。如圖2所示。

(a) 大區域覆蓋漏洞

(b) 小區域覆蓋漏洞圖2 單元格中的覆蓋漏洞

在選擇的傳感器節點和單元格邊緣之間通過應用三角形方法測量來計算漏洞面積，將傳感器節點連接到最近的單元邊緣直線坐標上，然后我們得到若干個三角形，如圖3所示。在圖3(a)大區域漏洞劃分4個三角形，圖3(b)小區域漏洞劃3個三角形，也可能存在漏洞區域劃分2個三角形和1個三角形。

(a) 大區域覆蓋漏洞劃分4個三角形

(b) 小區域覆蓋漏洞劃分3個三角形圖3 覆蓋漏洞劃分為多個三角形

根據三角測量理論，計算出劃分成多個小三角形的面積之和即可獲得漏洞面積，例如對圖3(a)大區域漏洞劃分4個三角形及其中某個三角形標注如圖4所示。

(a) 劃分多個三角形標注

(b) 三角形以及弓形標注圖4 劃分為三角形

依據海倫公式，計算圖4(b)三個點(X0,Y0)、(Xa,Ya)和(Xb,Yb)所圍成三角形的面積S0計算式表示為：

(3)

式中：r是傳感器感知半徑；Z是三角形半周長。但是按三角形計算，將減少或者增加覆蓋漏洞面積，因此需要計算傳感器感知半徑與邊L3所對弧長包圍的弓形面積S1，其計算式表示為：

(4)

最終獲得邊L1、L2與覆蓋漏洞區域所圍成的面積Sholes表示為：

Sholes=S0-S1

(5)

因此通過增加弓形面積的計算，可以精確獲得覆蓋漏洞區域的面積。在單元格中到某個頂點的覆蓋漏洞面積可以通過求所劃分單個三角形以及弓形的面積之差獲得；重復計算單元格的覆蓋漏洞到同一單元的四個邊緣，即可獲得整個單元格中的任何覆蓋漏洞區域面積Sall。

2 方向感知粒子群算法

2.1 基本粒子群算法

基本粒子群算法[12]在搜索空間中更新速度和位置公式表示為：

(6)

式中：r1∈(0,1)和r2∈(0,1)為相互獨立的隨機函數；vi,j(t)為第i個粒子在第t次迭代的第j維速度；xi,j(t)為第i個粒子在第t次迭代的第j維位置；t為迭代次數；pi,j為當前最佳解；gg,j為歷史最佳解；ω為權重；c1和c2分別為調節pi,j和gg,j的加速參數。

2.2 對比策略

在基本粒子群算法中，任何粒子都使用自身認知項c1r1[pi,j-xi,j(t)]和群體認知項c2r2[gg,j-xi,j(t)]來移動，當粒子的適應度值提高時[13]，跟蹤具有導向性的粒子更新pi,j。基本粒子群算法存在兩個缺點：① 如果具有導向的粒子陷入當前最優狀態，則粒子的往復運動完全浪費，增加處理時間；② 粒子趨于過早收斂。

在對比策略中，主要進行粒子的適應度函數值Fi(t)與自身當前最佳值pi比較：粒子i當前處于個體自身當前最佳值pi，若Fi(t)≥pi，則粒子處于極好狀態，飛行速度vnew極小范圍內更新即可；若Fi(t)≤Fi(t-1)且Fi(t)≥pi，粒子處于較好狀態，飛行速度vnew更新較小范圍即可；若Fi(t)≥Fi(t-1)，粒子處于收縮狀態，飛行速度vnew需要較大范圍更新。下面給出不同情況下的不同更新策略，其中rand是(0,1)中的隨機數。

(1) 當Fi(t)≥pi時，則更新策略表示為：

(7)

(2) 當Fi(t)≤Fi(t-1)且Fi(t)≥pi時，則更新策略表示為：

(8)

(3) 當Fi(t)≥Fi(t-1)時，則更新策略表示為：

(9)

2.3 粒子群適應度函數

覆蓋漏洞面積檢測率是覆蓋區域中漏洞的面積與覆蓋總面積Sall的比值，是評價無線傳感器網絡覆蓋漏洞檢測的重要指標[14-15]。所給方案將覆區域分解為L×H個單元格，按照式(3)、式(4)和式(5)計算每個單元格的覆蓋漏洞面積SL×H，獲得覆蓋漏洞面積檢測率η為：

(10)

所給方案把η轉化為求解Fi(t)最大值問題，在粒子群在迭代過程中，當η越小時，網絡存在的覆蓋漏洞越小，此時Fi(t)越大：

Fi(t)=1-ηi(t)

(11)

IPSO的主要步驟如下所示：

第1步：粒子群參數初始化；

第2步：無線傳感器網絡隨機化，覆蓋區域劃分若干單元格；

第3步：粒子群按照式(6)、式(7)、式(8)和式(9)更新位置以及速度；

第4步：達到最大迭代次數，或η≤3%，則進行第5步，否則轉第3步；

第5步：輸出檢測結果。

3 實驗仿真分析

利用MATLAB 7.0軟件進行仿真，傳感器節點數量為150個，部署矩形區域為200 m×200 m，每個節點的通信半徑為20 m，感知半徑為10 m，在部署區域中隨機設置19個大小不同的覆蓋漏洞，所有覆蓋漏洞的面積之和占部署區域總面積的3%。其中，粒子群參數為：c1=c2=1.4，ω=0.9-(tmax-t)/(0.5×tmax)，最大迭代次數為tmax=200，粒子總數量為300個。

3.1 單元格與漏洞個數、面積關系

在固定的監測區域內，劃分單元格邊長L和H的大小不同，其覆蓋漏洞個數和面積也呈現出一定的變化規律。L和H設置分別為：①L=2 m，H=2 m；②L=7 m，H=7 m；③L=10 mm，H=10 m；④L=13 m，H=13 m；⑤L=15 m，H=15 m；⑥L=20 m，H=20 m。通過50次蒙特卡羅隨機部署節點仿真實驗，檢測得到的覆蓋漏洞個數和面積結果如圖5所示。

(a) 單元格與檢測漏洞個數關系

(b) 單元格與漏洞面積檢測率η關系圖5 單元格與檢測漏洞個數、面積關系

由圖5(a)可以看出，隨著劃分單元格邊長為L和H逐漸變大，檢測漏洞個數在增加，邊長越靠近感知半徑時，檢測漏洞個數逐漸趨于真實值；由圖5(b)可以看出，隨著劃分單元格邊長為L和H逐漸變大接近感知半徑，漏洞面積檢測率η在減少，邊長越離感知半徑越大時，則檢測η越偏離實際值。單元格邊長越接近感知半徑時，則越有利于漏洞個數、面積檢測。

3.2 粒子數量、迭代次數與漏洞數量檢測比

在單元格邊長為L=H=10 m條件下，漏洞數量分別設置為4、6、8、10和12個，則粒子數量、迭代次數與漏洞數量檢測比如圖6所示。

(a) 粒子數量與漏洞數量檢測比

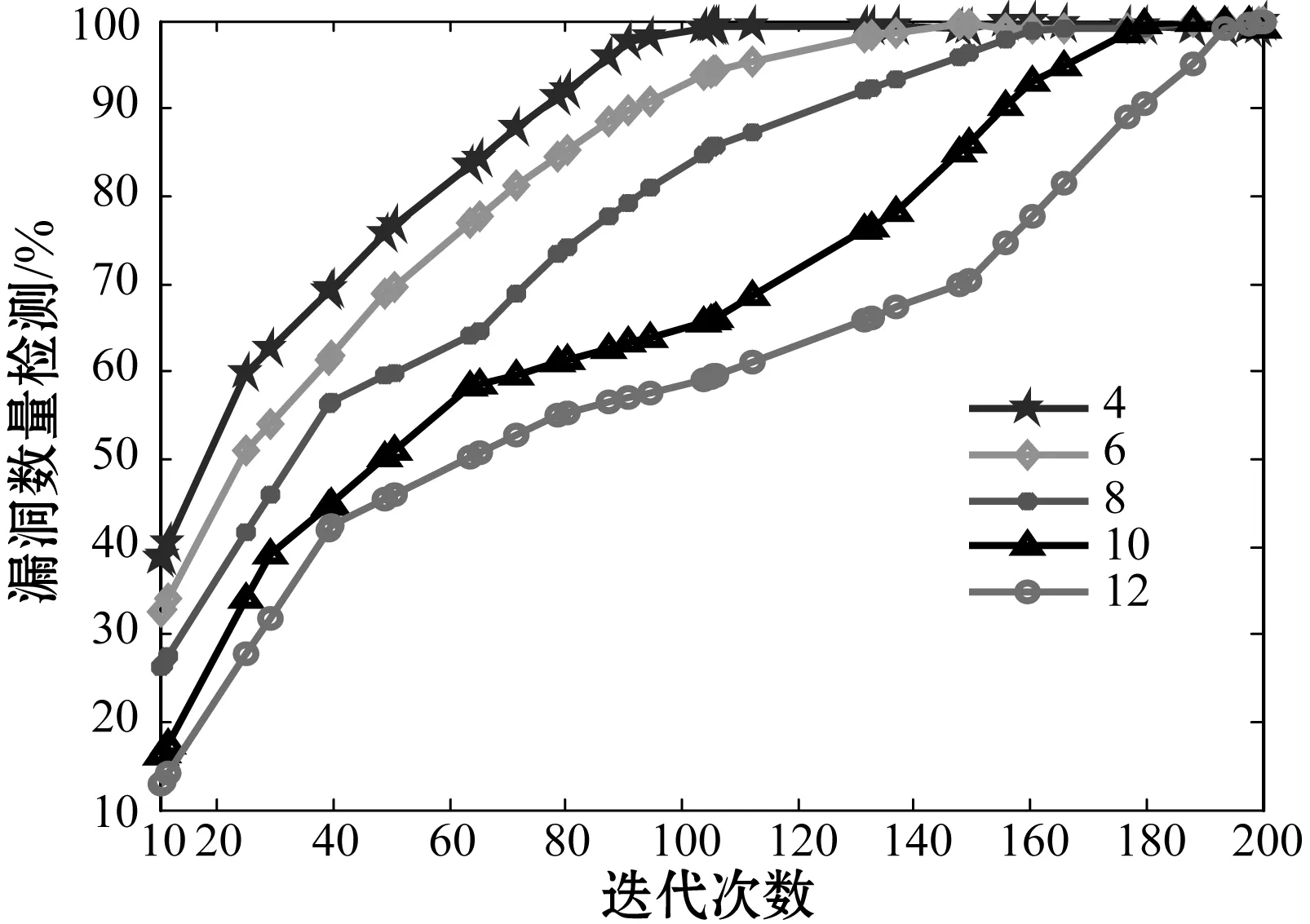
(b) 粒子迭代次數與漏洞數量檢測比圖6 粒子數量、迭代次數與漏洞數量檢測比

由圖6(a)可以看出，隨著粒子數量的增加，漏洞數量檢測比在逐漸提高，在相同粒子數量條件下，漏洞數量越多，則檢測比越差，在漏洞數量為4個時、粒子180個時，檢測比即可達到100%，在漏洞數量為12個時，需要粒子260個時，檢測比才能達到100%；由圖6(b)可以看出，在漏洞數量為4個時，粒子迭代次數為95次左右時，檢測比即可達到100%，在漏洞數量為12個時，粒子迭代次數為190次左右時，檢測比才能達到100%。這是因為當粒子群的數量增加時，越有利于發現無線傳感器網絡中的漏洞，同時漏洞數量越多，則需要迭代次數也隨之增加。

3.3 檢測指標對比分析

檢測指標分析主要包括漏洞面積檢測率和處理時間，用于對比分析的相關算法主要有HA、NTA、GDA、VGA、CDA、PSO和IPSO，每種算法各進行40次蒙特卡羅仿真實驗，結果如圖7所示。

(a) 漏洞面積檢測率

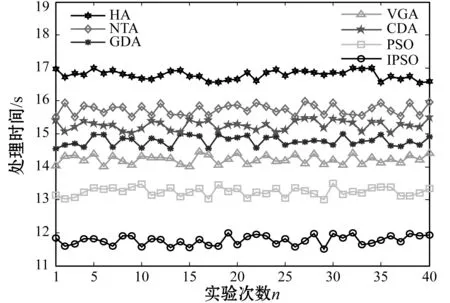
(b) 處理時間圖7 檢測指標對比分析

可以看出，IPSO對覆蓋漏洞面積檢測、處理時間相比其他算法具有優勢，這主要是由于IPSO考慮了單元格中弓形面積對覆蓋漏洞面積的影響，使得覆蓋漏洞面積檢測率更加符合真實值，粒子群在進行粒子的適應度函數值與自身當前最佳值比較過程中，采取不同的更新策略，防止了粒子尋優的盲目性。下面通過分析漏洞檢測率與檢測時間的關系來驗證所給方案更新策略的有效性，如圖8所示。可以看出，IPSO所需的監測時間最少，而且隨著漏洞檢測率的提高，IPSO的檢測時間增加也最少，這主要是由于IPSO采用新的更新策略，通過比較粒子的適應度函數值和自身當前最佳值，及時調整粒子的飛行速度和位置，能夠更快速地檢測出漏洞。由此說明，IPSO的更新策略是有效的。

圖8 IPSO更新策略的有效性分析

4 結 語

為提高無線傳感器網絡覆蓋漏洞的監測效果，采用改進粒子群算法對無線傳感器網絡漏洞檢測。所給方案首先對覆蓋區域劃分不同單元格，單元格頂點劃分成多個小三角形的面積與弓形的面積之差獲得漏洞面積，然后利用改進粒子群算法進行粒子的適應度函數值與自身當前最佳值比較，獲得不同的更新速度與位置。實驗仿真得出單元格邊長越接近感知半徑越有利于漏洞個數、面積檢測。而且相比于其他算法，所給方案在漏洞面積檢測上處理時間也具有優勢。