基于數據挖掘的汽車生產線螺栓打緊異常識別*
安 猛,孟新宇,陳長征,安文杰
(沈陽工業大學 機械工程學院,遼寧 沈陽 110027)
0 引言
在汽車零件裝配過程中,螺栓聯接是最基礎、最廣泛、標準化最高的連接方式。整車裝配時,一輛汽車大概有4 000個~6 000個螺紋聯接部件[1],螺栓聯接在汽車裝配中發揮著重要的作用,有些甚至關系到人身安全。汽車生產線上關鍵部位最常使用的螺栓打緊方法為 “扭矩轉角法”[2],這種方法依據最終扭矩判斷打緊是否合格,沒有對過程數據進行分析,但過程數據往往反映打緊質量。螺栓打緊過程曲線發生較大變化時,雖然打緊結果能滿足要求,但過程存在異常;出廠檢驗及用戶使用時也證明打緊過程異常的螺栓多為不合格的故障螺栓[3]。本文主要對螺栓打緊過程進行研究,針對這種潛在的質量隱患,通過建立異常狀態識別模型對其進行判別并及時做出提示。
實驗數據為某一工位螺栓打緊數據集,打緊設備內有傳感器,實時記錄過程數據,主要包括過程的轉角值和扭矩值、打緊時間等。對打緊樣本數量統計,總樣本為19 000條,正常樣本為18 800條,異常樣本為200條,僅占樣本總體的1.05%,異常樣本數量少且占比小,樣本存在著類間不平衡問題。其中異常樣本有兩種:一種是打緊結果不合格樣本,打緊設備可以識別;另一種是打緊結果合格,但過程異常,出廠檢測時不符合要求,需要長時間反饋[4]。
1 數據處理
1.1 除噪
原始螺栓打緊過程數據如圖1所示。原始數據易受到外界噪聲干擾,導致類別間的特征顯著性降低,影響特征提取[5],過程數據在時間維度也有一定漂移,因此建模前需要對原始數據進行處理。

圖1 原始螺栓打緊過程數據 圖2 部分處理后的數據 圖3 按固定角度切分扭矩
依據螺栓打緊工藝,清除停頓產生的噪聲及打緊結束后引入的噪聲。過程數據點計為{(Ai,Ti)∣i∈[1,n]},表示第i個打緊過程,Ai為轉角值,Ti為扭矩值,n為數據點的個數。依據打緊過程中噪聲扭矩值遠小于左右兩側扭矩的特點除噪,以i=1為起點,遍歷數據集所有數據點。步驟如下:
(1) 差分計算每一個數據點,即Ti在i處一階差分ΔTi為:
ΔTi=Ti+1-Ti.
(1)
(2) 當ΔTi<0時,把第i個數據點記作(Aflag,Tflag),依據式(2)計算出ΔTflag,對滿足ΔTflag≤0條件的(Ai,Ti)進行標記。
ΔTflag=Ti+1-Tflagi∈(flag,n).
(2)
(3) 當ΔTflag>0時,重復(2)、(3)步驟,直到遍歷所有數據點并去掉標記數據。
當扭矩達到設定的最大值附近時,即視為打緊結束,記打緊結束點為(Af,Tf),理想狀態下結束點為(Ad,Td),求得二者差值為S=Af-Ad,當S>0時,向左移動|S|個單位,當S<0時,向右移動|S|個單位。對所有過程樣本進行此操作,完成主體數據集中。部分處理后的數據如圖2所示。
1.2 特征提取
數據集直接特征為扭矩值[6],打緊時扭矩有較大變化,對過程扭矩值特征進行提取。采集數據時,轉動速度是變化的,不能利用采樣點分割過程曲線,但轉過的角度值A是固定的,現提出一種按角度值切分扭矩、提取特征的方法[7,8]。如圖3所示,將過程曲線按一定角度切分,每個區域為一個目標窗口,計算窗口里扭矩平均值,將轉角、扭矩轉化為一定長度的扭矩向量[9]。第i條過程曲線扭矩向量Ti為:
Ti=[t1,t2,…,tA].
(3)
其中:tA為螺栓轉動角度(A-1,A]中的扭矩均值。這樣數據集由{(Ai,Ti)|i∈[0,n]}變為{Ti|i∈[0,A]}。在螺栓轉動角度 [36°,58°]的范圍內,以1°的間隔切分扭矩,可獲取22個特征值。
2 模型算法
2.1 評價指標
在評價分類器性能時,基于混淆矩陣提出不平衡數據學習指標[10]。二分類中,分類結果為4種情況,如表1所示。

表1 二分類混淆矩陣
(1) ACC(分類精度)。ACC為分類正確的樣本與分類器分類樣本的比值,定義為:
(4)
(2) 特異性(Specificity)。特異性為分類器對少數樣本的敏感程度,數值越大,對少數類樣本分類性能越好,定義為:
(5)
(3) G-means。G-mean為多數類和少數類樣本分類準確度的集合平均值,其可以合理評價整體分類性能,定義為:
(6)
(4) AUC面積(Area Under the Curve)。以FP/(FP+TN)為橫坐標,TP/(TP+FN)為縱坐標,繪制ROC(Receiver Operating Characteristic)曲線[11],中文名為“受試者工作特征曲線”,假設ROC曲線上有n個數據點,AUC定義為:
(7)
其中:x為TP/(TP+FN);y為Specificity。 AUC值一般在[0.5,1],數值越大說明分類器性能越好。
2.2 SMOTE改進算法
原SMOTE算法存在兩方面問題[12-14]:合成的新樣本只是來自兩個少數樣本對應的線段上,潛在出現范圍僅在此線段上;在維度較高的特征空間中,對潛在少數樣本的分布不足以完全描述。本文數據特征向量為22,維度較高,原SMOTE算法不再適用,需要改進。
改進思路是通過D個少數樣本合成新樣本,D是特征空間維數。首先,計算少數類樣本k個同近鄰樣本,選取其中D個樣本,以 0到1/D的權值對其矢量加和構建新樣本。新樣本空間從一維擴展到D維,下面是改進算法的具體流程。
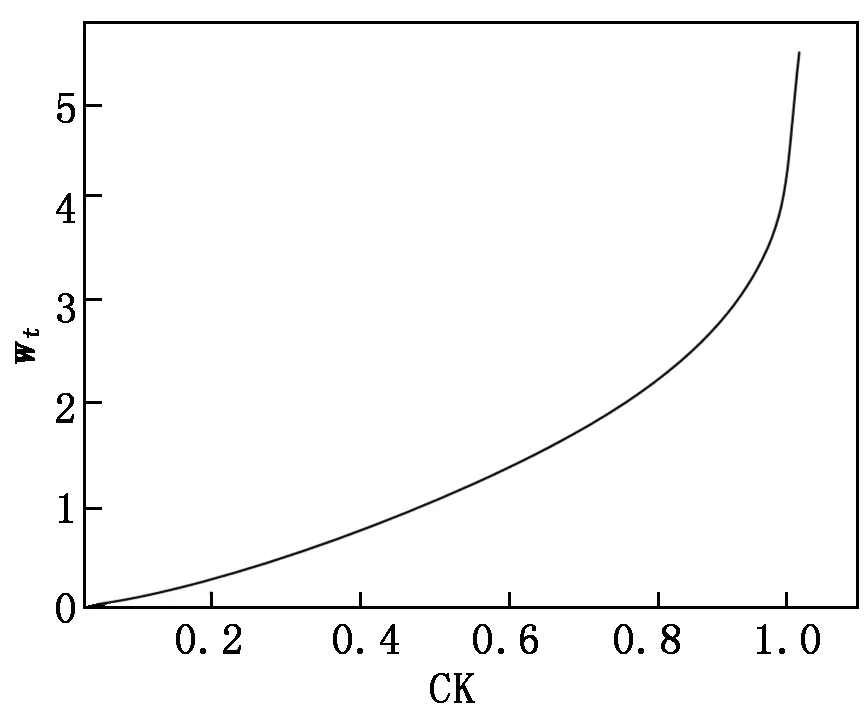
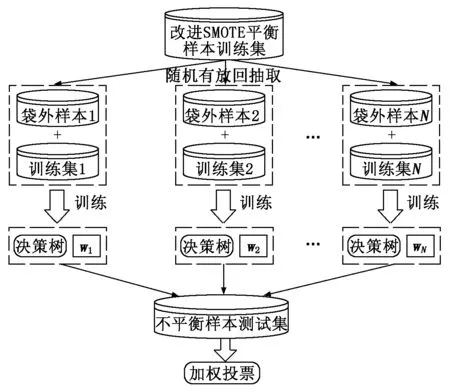
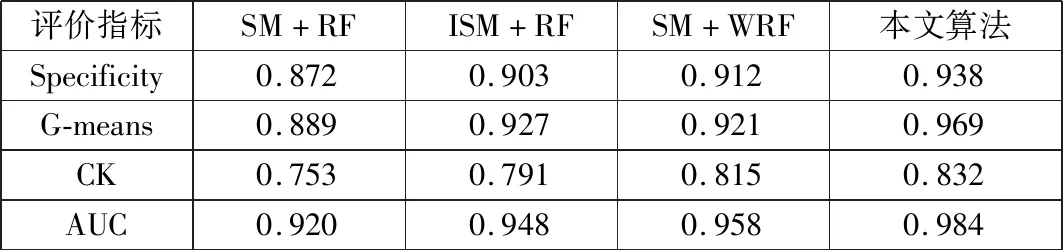
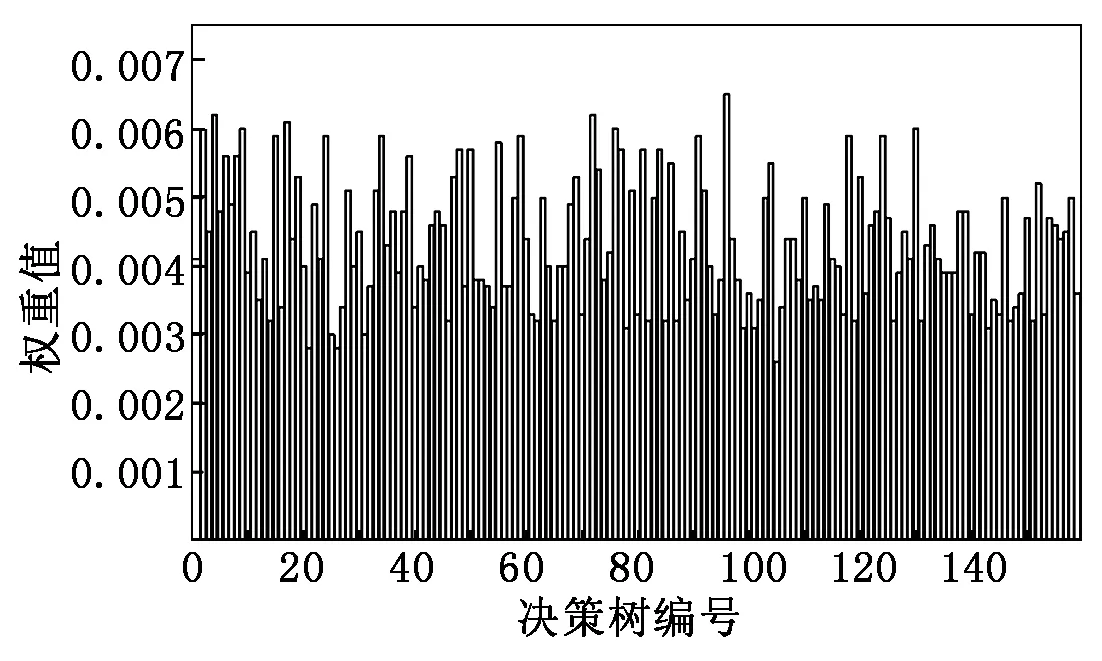
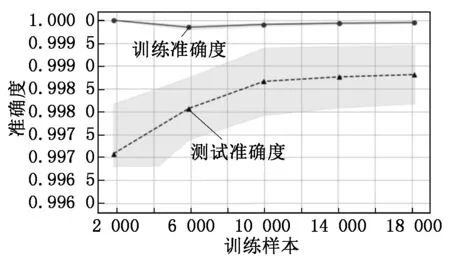
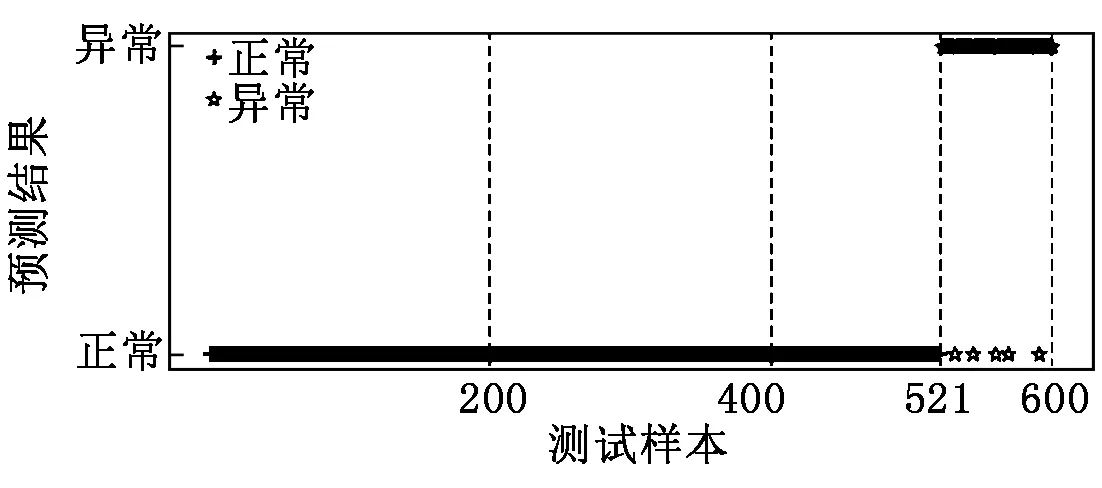
首先輸入以下參數:P={P1,…,Pn},為訓練集中少數類樣本集合;Pa為P中的一個樣本;n為少數類樣本個數。設k為近鄰個數;D為參與合成新樣本的近鄰個數,D 接著,完成以下算法: (1) 利用集合P構建Kd樹; (2) fori=1 tondo; (3) 通過Kd樹找出Pi的k近鄰:Kni={kni1,kni2,…,knik}; (4) fora=1 toNdo; (5) 在Kni中隨機選取D個近鄰樣本:Kn′a={kn′a1,kn′a2,…,kn′aD}; (6) 在[0,1/D]中隨機選取D個實數(能夠重復):da={da1,da2,…,daD}; (7) 計算被選取的近鄰樣本和Pa的向量差:vecan=kn′an-Pa; (9) 新樣本加入集合:newa→Samples; (10) End for。 最后輸出:新樣本集Samples。 如圖4所示,P點為合成新樣本的目標樣本點,A和B為兩個同類近鄰樣本點,C和D為合成樣本點。圖4(b)中,A、B樣本點的合成權值為dA、dB,取值范圍(0,0.5],特征向量P′=P+dA(A-P)+dB(B-P)。平行四邊形邊長分別為0.5PA與0.5PB,合成的新樣本C、D位置范圍在平行四邊形內。而在圖4(a)中,原算法生成的樣本點C、D在PA和PB線段間。 圖4 算法改進前、后對比圖 一個已訓練完的隨機森林模型[15-17]決策樹數量為T,測試集為X,類別數為C,模型輸出為: (8) 其中:ht(X)為第t棵決策樹的輸出;I(·)為一個指示函數。 由式(8)可知,每棵決策樹投票權重都為1,但各決策樹的分類準確度不同[18]。對此本文提出了加權隨機森林模型,即在訓練時評估出每棵決策樹的分類性能,并根據性能賦予對應權重,在投票時,乘上對應的權重值,能夠降低訓練精度不高的決策樹對整個模型的影響。因此,公式(8)可改寫為: (9) 其中:wt為第t棵決策樹的權重值。 利用袋外樣本[19]作為每棵決策樹的測試集來評估分類性能,并據此結果賦予相應權重,使性能好的決策樹擁有更重要的位置。 使用Kappa系數(CK)評價決策樹整體分類性能,CK是評價一致性程度的指標,能夠考慮到各種漏分與錯分樣本,能表示分類與隨機分類錯誤減少的比例。一般情況下CK為(0,1),CK值越大,說明結果與實際結果越一致,分類器性能越好[20]。CK由下式計算: (10) 其中:CKc為分類的偶然一致性比率,計算公式如下: CKc= (11) 為了把較大的權重分配給性能更優的分類器,文獻[21]指出:一組相互獨立的分類器L1,L2,…,LM,準確度為p1,p2,…,pM,各分類器的權重與相應準確度關系如式(12)所示: (12) 將式(12)中的p替換成CK,其中CK的取值范圍為(-1,1),公式(12)可改寫為: (13) 依據公式(13),決策樹的CK值越大,其分配到的權重也越大,對最終投票結果影響也越大。CK與wt的關系如圖5所示。可將式(13)代入式(9),從而得到最終的輸出結果。加權隨機森林算法流程如圖6所示,根據得到的CK值決定每棵樹的投票權重,降低分類性能差的決策樹對最終結果的影響,輸出的結果更合理,也能夠提高整體的分類性能。 圖5 CK與wt的關系 圖6 加權隨機森林算法流程 本文算法均使用Python語言編寫,在Jupyter notebook平臺上調試并測試。為驗證改進的SMOTE和加權隨機森林算法對螺栓打緊數據集分類效果的影響,將SMOTE(SM)、改進SMOTE(ISM))、隨機森林(RF)、加權隨機森林(WRF),根據不同的組合形成不同算法模型,即SM+RF、ISM+RF、SM+WRF與本文的ISM+WRF模型。在經處理后的打緊數據集上,實驗這4種算法,并對得到的結果進行比較。 根據不同算法建立模型并訓練、測試,結果如表2所示,ISM、WRF與SM、RF相比,都能提高分類結果的Specificity,表明經過改進的算法都能提高少數類樣本的分類準確性。從SM+RF和SM+WRF的對比結果看出,數據集的G-mean、CK和AUC均有提升,與未改進的SM+RF算法相比,SM+WRF算法的G-mean提升了3.6%,CK提升了8.23%,AUC提升了3.8%,說明加權隨機森林比傳統隨機森林的分類性能更好。從SM+RF和ISM+RF的對比結果也可看出,ISM對數據集的分類效果也有提升,各指標均提高3%以上,也說明改進的SMOTE算法比原算法的分類性能更好。從數據層面改進的ISM與從算法層面改進的WRF對分類效果均有提升,結合ISM和WRF的算法模型對不平衡數據集的少數類及整體分類效果最好,在螺栓打緊數據集非常適用。 表2 不同算法與本文算法分類結果對比 對ISM+WRF模型調參至最優,獲得159棵決策樹并求得各決策樹權重值,如圖7所示,數值范圍在[0.002,0.007]。不同的決策樹分類性能不一致,對隨機森林的貢獻不同,權重值也不同。繪制參數調優后模型的學習曲線,如圖8所示,當數據增加時,訓練集分類準確性曲線(虛線)和測試集預測準確性曲線(直線)靠的較近但有一定距離,并隨數據增加相持平,最后收斂于0.998以上,說明模型不過擬合也不欠擬合,效果較好。 圖7 加權隨機森林決策樹權重值 圖8 隨機森林模型學習曲線 對螺栓異常狀態識別模型進行實驗驗證,在打緊數據庫提取600條樣本,其中正常樣本521條,異常樣本79條,輸入到模型中得出識別后的結果,如圖9所示。由圖9可知,所有打緊正常螺栓及74條打緊異常螺栓被正確識別,僅5條打緊異常螺栓被誤分到正常類中,對打緊異常螺栓識別率達93%以上,說明模型識別打緊異常螺栓效果較好。 圖9 測試效果 汽車生產線上螺栓打緊設備的打緊結果只通過最終扭矩值判斷,缺乏對過程數據分析,會漏掉少量打緊異常螺栓。出廠檢測時,發現異常螺栓,多為不合格螺栓,需重新打緊,影響生產效率,增加生產時間和成本。同時,打緊質量在檢測和初期使用中也難以評估,本文提出的螺栓打緊異常狀態識別模型是針對過程,能夠有效識別異常螺栓,并及時采取措施。在后期研究中,探索打緊過程與打緊質量的關系將成為分析螺栓聯接質量的一種新途徑。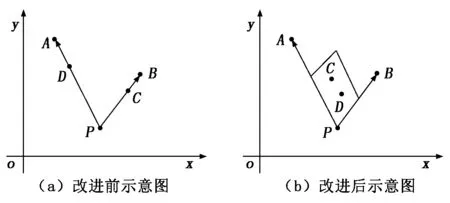
2.3 加權隨機森林算法
3 建立模型并驗證
3.1 算法對比結果
3.2 實驗驗證
4 結論

