基于改進GWOLSTM的船舶主機性能預測模型

石彪　王海燕　焦品博

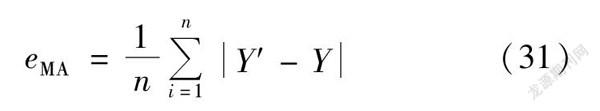
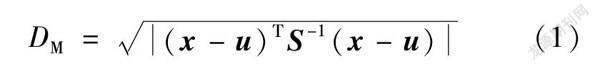
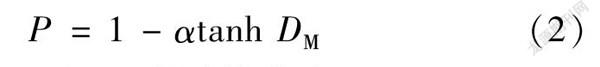
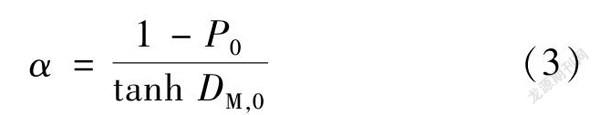
摘要：為提高船舶主機性能預測的精度，更好地幫助輪機員制定主機的維修保養計劃，提出一種利用改進灰狼優化算法（grey wolf optimizer， GWO）對長短期記憶網絡（long shortterm memory network， LSTM）進行優化的船舶主機性能預測模型，簡稱為改進的GWOLSTM模型。基于Metropolis接受準則的思想，在傳統GWO中引入一種隨機搜索機制來解決傳統GWO前期收斂速度慢和后期易陷入局部最優的問題。分別建立單步預測模型和多步預測模型。與GWOLSTM和傳統LSTM的預測結果進行對比，結果表明，改進GWOLSTM單步預測的均方根誤差分別降低了3236%和5038%，多步預測的均方根誤差分別降低了2616%和3557%。

關鍵詞：? Metropolis接受準則; 長短期記憶網絡（LSTM）; 灰狼優化算法（GWO）; 性能預測

中圖分類號：? U6641211文獻標志碼：? A

Prediction model of marine main engine performance

based on improved GWOLSTM

Abstract： In order to improve the prediction accuracy of marine main engine performance and help engineers make better maintenance plan of main engines， a prediction model of marine main engine performance is proposed， where the improved grey wolf optimizer （GWO） is used to optimize the long shortterm memory network （LSTM）. The model is called a modified GWOLSTM for short. Based on the idea of Metropolis acceptance criterion， a random search mechanism is introduced to the traditional GWO to solve the problem of slow convergence speed in the early stage and being easy to fall into the local optimum in the later stage of the traditional GWO. The onestep prediction model and the multistep prediction model are established， respectively. Compared with the GWOLSTM and the traditional LSTM， the results show that， the root mean square error of the onestep prediction of the improved GWOLSTM is reduced by 3236% and 5038%， respectively， and the root mean square error of the multistep prediction of the improved GWOLSTM is reduced by 2616% and 3557%， respectively.

Key words： Metropolis acceptance criterion; long shortterm memory network （LSTM）; grey wolf optimizer （GWO）; performance prediction

引言

船舶主機作為船舶的心臟，長期處于復雜多變的工作環境中，運行時間越長其工作性能就越差。掌握主機性能變化趨勢，有助于輪機員制訂維修保養計劃[1]，不僅可以預防故障的發生，還能減少停機、停航時間，節約成本。

船舶主機性能受多種因素影響，對船舶主機性能變化的預測是一種復雜且不穩定的非線性問題。目前，主機性能趨勢的預測方法由基于模型驅動逐漸轉變為基于數據驅動。基于模型驅動的方法過于復雜，且泛化性能較差，很難處理非線性問題。在基于數據驅動的方法中，循環神經網絡（recurrent neural network，RNN）因其具有特殊的網絡結構而適合處理這種非線性問題，并且由于RNN還引入了時序的概念，它能更好地分析主機性能變化趨勢。1997年HOCHREITER等[2]對RNN的結構做了進一步的改進，提出了長短期記憶網絡（long shortterm memory，LSTM），不僅有效地緩解了RNN中梯度爆炸和梯度消失的問題，而且解決了RNN的長時依賴的問題。

近年來，LSTM在船舶設備性能、壽命等方面的評估中得到了廣泛的應用。王子銘等[3]使用LSTM建立了船舶主機油耗實時預測模型，結果表明該模型預測結果可靠、誤差較小。易文海等[4]使用LSTM建立波浪與船舶的因果關系模型，對隨機橫浪中船舶的橫搖運動進行短期預測，結果表明此方法可行。QIAO等[5]使用LSTM實時預測動態系泊線響應，結果表明該方法預測精度較高。SHI等[6]利用LSTM對船舶柴油機的整體性能做了預測，結果表明該方法可以用于船舶性能的短期預測和長期預測。

LSTM在訓練數據時普遍使用隨時間反向傳播（back propogation through time，BPTT）算法，但該算法因復雜度較高、學習效率低而效率低下。灰狼優化算法（grey wolf optimizer，GWO）作為啟發式算法的一種，相比于其他啟發式算法具有結構簡單、容易實現和需要人為調整的超參數較少的優點[78]，適合用于本文的研究。基于此，本文提出用GWO代替BPTT算法尋優的思路，針對傳統GWO前期收斂速度慢和后期易陷入局部最優的缺點，利用Metropolis接受準則思想提出隨機搜索機制，對GWO的結構進行改進。使用改進后的GWO來優化LSTM，提高船舶主機性能預測精度。

1主機性能指標

1.1監測參數與數據來源

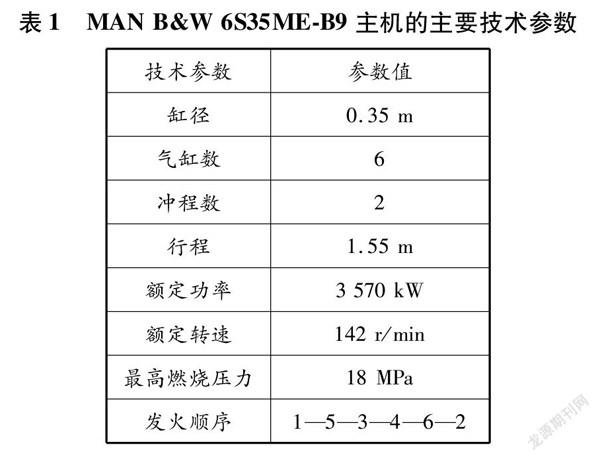
本文研究數據采集于上海海事大學自動化機艙實驗室，采集對象是MAN B&W 6S35MEB9型號的主機，該主機的主要技術參數見表1。

綜合信息系統通過傳感器收集監測參數，參數經過處理后保存至數據庫。傳感器采樣間隔時間為1 min。柴油機的轉速和功率信號通過磁電式測試儀采集，溫度信號由pt100溫度傳感器采集，壓力信號由壓力變送器采集。

1.2性能參數選擇

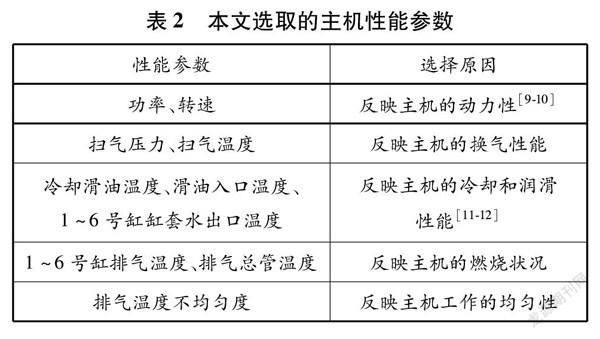
影響船舶主機性能的熱力參數眾多，合理選擇熱力參數是預測船舶主機性能的前提。本文的主機監測數據均是在實驗室固定環境下采集的，因此環境溫度、環境壓力、環境濕度等外界參數可以視為固定不變。本文選取的主機性能參數見表2。

表2本文選取的主機性能參數性能參數選擇原因功率、轉速反映主機的動力性[910]掃氣壓力、掃氣溫度反映主機的換氣性能冷卻滑油溫度、滑油入口溫度、

本文參數的選擇基于兩個方面的原因：一是便于采集，不需要加裝額外的傳感器;二是輪機員也依靠這些參數來判斷主機的性能狀況。

1.3性能指標

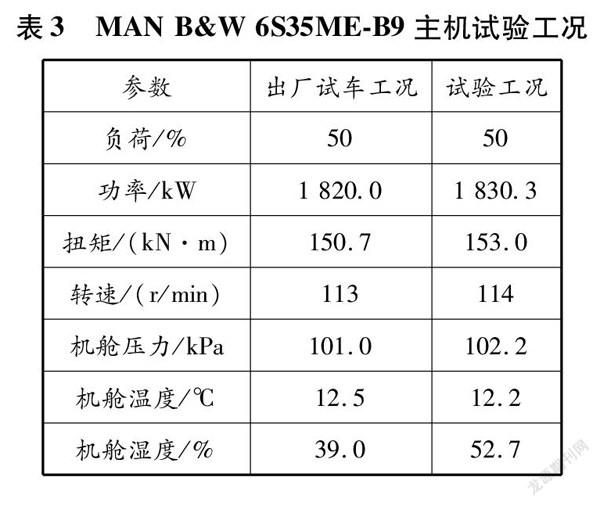
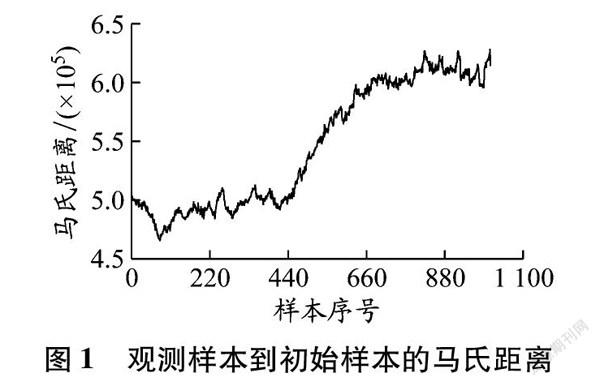
采集該主機運行1745 h的性能數據作為數據源，對數據處理后，選取50%負荷、轉速穩定在114 r/min下的數據作為觀測樣本，觀測樣本共1 009個，每個樣本均含有20個性能數據。以主機出廠試車數據中50%負荷試車工況（見表3）下的100組試車樣本數據作為初始性能樣本，計算觀測樣本到初始性能樣本的馬氏距離。馬氏距離可以描述兩個樣本之間的偏離程度。柴油機的性能參數具有量綱不同、變化不一和相關性強的特點，通過直接觀測多個性能參數判斷柴油機的工作狀態容易產生混亂，特別是在某些性能參數的變化與柴油機的整體性能變化不一致甚至趨勢相反時。馬氏距離的優勢在于：（1）馬氏距離的計算中包括樣本總體協方差的計算，它考慮了樣本的總體分布，消除了各變量之間的相關性;（2）馬氏距離不受數據量綱的影響，即兩點之間的馬氏距離與原始數據的測量單位無關。因此，本文用馬氏距離來表示柴油機性能的退化程度。馬氏距離越大，說明主機性能退化得越嚴重。馬氏距離數學表達式如下：（1）式中：DM為觀測樣本到初始樣本的馬氏距離;x為觀測樣本矩陣;u為初始樣本的均值矩陣;S-1為初始樣本的協方差矩陣。

為了較直觀地描述主機性能的退化過程，將馬氏距離歸一化成性能指標。性能指標值越小，說明主機性能退化越嚴重，其數學表達式如下：（2）式中：α為調節因子。α的計算式為（3）式中：P0為主機工作初期的性能指標值;DM，0為主機工作初期性能的馬氏距離。

根據式（1）計算觀測樣本到初始樣本的馬氏距離。從圖1可以看出，隨著運行時間的增加，馬氏距離越來越大。在0號樣本處，DM為529×105，說明此時主機的整體性能已經遠遠偏離初始性能，且處于退化加劇期。柴油機性能退化過程主要有兩個階段：一是緩慢退化期，此階段柴油機性能接近其出廠性能，馬氏距離較小;二是退化加劇期，此階段柴油機性能退化速度加劇，馬氏距離較大。

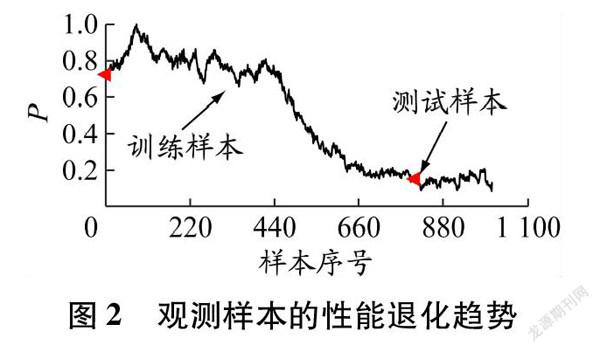
根據式（3）確定式（2）中的α值，再根據式（2）將不同時刻的DM歸一化成P。當α=1.2時，P均勻分布在0與1之間。由圖2可以看出，主機性能曲線整體上呈下降趨勢，表示主機性能逐漸退化。

將前80%的觀測樣本作為訓練樣本進行模型訓練和參數調整，后20%的觀測樣本作為測試樣本進行模型評估和預測結果分析。

2預測模型

本文首先對傳統GWO的結構進行改進，然后在改進GWO的基礎上建立改進GWOLSTM船舶主機性能預測模型。

2.1LSTM

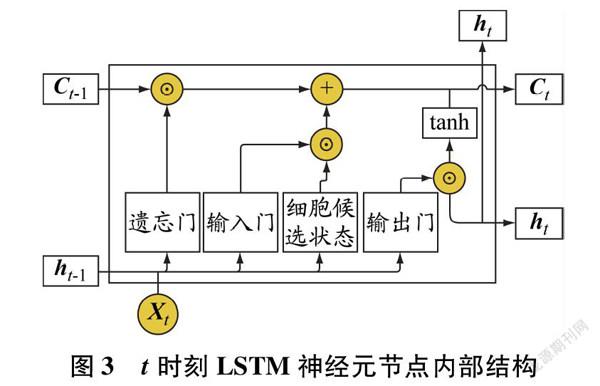
LSTM與RNN最大的不同在于，LSTM神經元中具有3個“控制門”和2種狀態，見圖3。在這種結構下，LSTM的細胞狀態可以隨時間進行信息傳遞，并通過“門”增刪信息，使得LSTM具有記憶功能[13]。

首先，遺忘門進行信息篩選，剔除掉部分信息，公式如下：（4）式中：ft為t時刻神經元的遺忘門矩陣;Wf為遺忘門權重矩陣;Xt為t時刻神經元的輸入矩陣;ht-1為t-1時刻神經元的隱藏狀態輸出矩陣;bf為遺忘門偏置矩陣。

其次，輸入門決定細胞狀態的哪些信息被保留，表達式如下：（5）

（6）

（7）式中：It為t時刻神經元的輸入門矩陣;C～t為t時刻神經元的細胞候選狀態矩陣;Ct為t時刻神經元的細胞狀態矩陣;WI為輸入門權重矩陣;bI為輸入門偏置矩陣;Wc為細胞候選狀態權重矩陣;bc為細胞候選狀態偏置矩陣;⊙為矩陣的點乘。

最后，輸出門決定當前時刻神經元的輸出，表達式如下：（8）

（9）式中：ot為t時刻神經元的輸出門矩陣;Wo為輸出門權重矩陣;bo為輸出門偏置矩陣;ht為t時刻神經元的隱藏狀態輸出矩陣。

2.2GWO

2014年，MIRJALILI等[14]提出一種新的群體智能優化算法——GWO。GWO通過模擬狼群中的等級制度，將狼群中的狼分為由高到低4個等級：Alpha、Beta、Delta和Omega。Alpha狼是狼群中唯一的領導者，領導著種群捕獵。捕獵分為3個階段：

（1）包圍。在Alpha狼的帶領下，狼群先包圍獵物，數學模型如下：（10）

（11）式中：下標i為迭代次數，i=0，1，…，n;D為灰狼與獵物之間的距離;Xp，i為迭代次數為i時的獵物位置向量;Xi為迭代次數為i時的灰狼位置向量;Xi+1為迭代次數為i+1時的灰狼位置向量;A和C為系數向量。A和C表達式為（12）

（13）式中：r1和r2為元素取值在區間[0，1]內的隨機向量;a為控制參數，隨迭代次數的增加從2線性減少至0。

（2）獵捕。狼群包圍獵物后，Alpha狼、Beta狼、Delta狼離獵物的距離最近，狼群將在Alpha狼、Beta狼和Delta狼的帶領下向獵物逼近，Omega狼的位置更新如下：（14）

（15）

（16）

（17）

（18）

（19）

（20）式中：Dα、Dβ、Dδ分別為當前Omega狼與Alpha狼、Beta狼、Delta狼之間的距離;Xα、Xβ、Xδ分別為Alpha狼、Beta狼、Delta狼的位置向量。

（3）進攻。該階段的目標是捕獲獵物，即獲得最優解。GWO通過減小a的值模擬逼近獵物的過程。當a逐漸減小時，A的元素取值也在[-a，a]區間內。當A<1時，狼群能夠攻擊到獵物;當A>1時狼群會向四周散去，導致狼群失去最優位置，這也是GWO容易陷入局部最優的原因[15]。

2.3改進GWO

GWO的缺點是前期收斂速度慢和后期易陷入局部最優[16]。本文借鑒模擬退火的Metropolis接受準則思想，對GWO的不足進行改進。Metropolis接受準則是指以一定的概率接受新狀態，從而使算法有能力跳出局部極值和避免過早收斂。接受新狀態的概率為

（21）

式中：p（ON）為從狀態O轉移為狀態N的概率;f（N）和f（O）分別為狀態O和狀態N的目標函數值;c為控制參數。

基于Metropolis接受準則思想，本文提出隨機搜索機制，即在灰狼種群圍捕獵物的過程中，賦予每只灰狼在自身一定范圍內的隨機搜索能力，當灰狼到達新位置時，對灰狼的新位置進行適應度值計算，然后與舊位置的適應度值進行比較。若新位置的適應度值小于舊位置的適應度值，灰狼將留在新位置;否則，灰狼返回舊位置。數學模型如下：（22）

（23）式中：f（Xi）為灰狼原位置的適應度值;f（Xi，new）為灰狼新位置的適應度值;vmax和vmin分別為解空間的上限和下限;r為隨機向量，其元素取值在[-1，1]區間內;w為隨機搜索因子。w由下式進行更新：

（24）

式中：inow和imax分別為當前迭代次數和最大迭代次數;wmax為最大搜索因子，設置為0.01;wmin為最小搜索因子，設置為0.001。

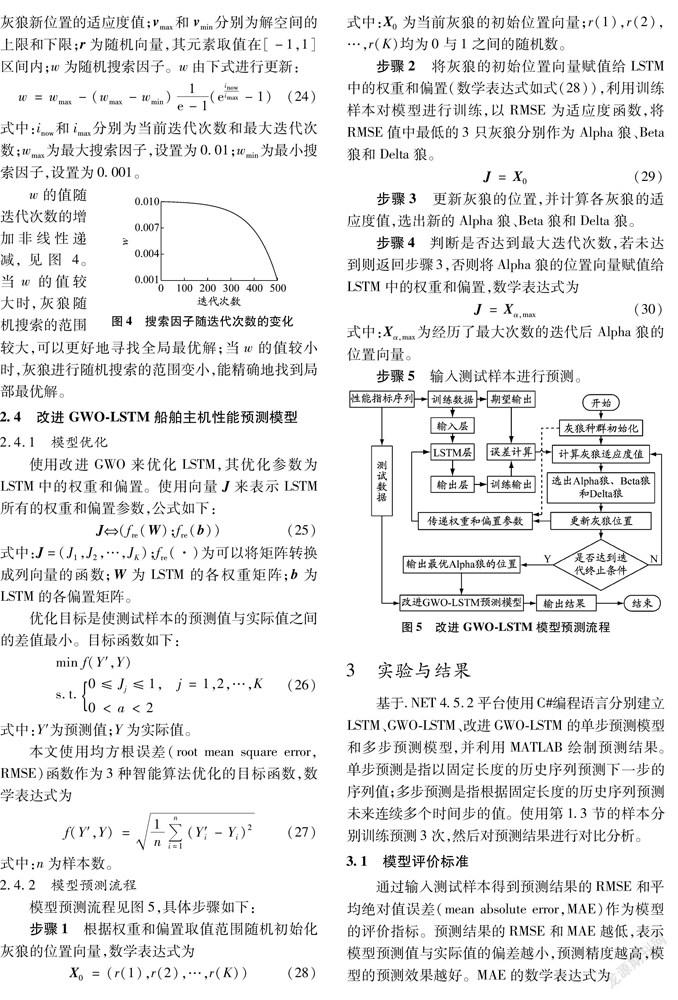
圖4搜索因子隨迭代次數的變化w的值隨迭代次數的增加非線性遞減，見圖4。當w的值較大時，灰狼隨機搜索的范圍較大，可以更好地尋找全局最優解;當w的值較小時，灰狼進行隨機搜索的范圍變小，能精確地找到局部最優解。

2.4改進GWOLSTM船舶主機性能預測模型

2.4.1模型優化

使用改進GWO來優化LSTM，其優化參數為LSTM中的權重和偏置。使用向量J來表示LSTM所有的權重和偏置參數，公式如下：（25）式中：J=（J1，J2，…，JK）;fre（·）為可以將矩陣轉換成列向量的函數;W為LSTM的各權重矩陣;b為LSTM的各偏置矩陣。

優化目標是使測試樣本的預測值與實際值之間的差值最小。目標函數如下：min f（Y′，Y）

（26）式中：Y′為預測值;Y為實際值。

本文使用均方根誤差（root mean square error，RMSE）函數作為3種智能算法優化的目標函數，數學表達式為f（Y′，Y）=1nni=1（Y′i-Yi）2（27）式中：n為樣本數。

2.4.2模型預測流程

模型預測流程見圖5，具體步驟如下：

步驟1根據權重和偏置取值范圍隨機初始化灰狼的位置向量，數學表達式為X0=（r（1），r（2），…，r（K））（28）式中：X0為當前灰狼的初始位置向量;r（1），r（2），…，r（K）均為0與1之間的隨機數。

步驟2將灰狼的初始位置向量賦值給LSTM中的權重和偏置（數學表達式如式（28）），利用訓練樣本對模型進行訓練，以RMSE為適應度函數，將RMSE值中最低的3只灰狼分別作為Alpha狼、Beta狼和Delta狼。（29）步驟3更新灰狼的位置，并計算各灰狼的適應度值，選出新的Alpha狼、Beta狼和Delta狼。

步驟4判斷是否達到最大迭代次數，若未達到則返回步驟3，否則將Alpha狼的位置向量賦值給LSTM中的權重和偏置，數學表達式為（30）式中：Xα，max為經歷了最大次數的迭代后Alpha狼的位置向量。

步驟5輸入測試樣本進行預測。

3實驗與結果

基于.NET 45.2平臺使用C#編程語言分別建立LSTM、GWOLSTM、改進GWOLSTM的單步預測模型和多步預測模型，并利用MATLAB繪制預測結果。單步預測是指以固定長度的歷史序列預測下一步的序列值;多步預測是指根據固定長度的歷史序列預測未來連續多個時間步的值。使用第1.3節的樣本分別訓練預測3次，然后對預測結果進行對比分析。

3.1模型評價標準

通過輸入測試樣本得到預測結果的RMSE和平均絕對值誤差（mean absolute error，MAE）作為模型的評價指標。預測結果的RMSE和MAE越低，表示模型預測值與實際值的偏差越小，預測精度越高，模型的預測效果越好。MAE的數學表達式為（31）

3.2模型參數設置

該改進GWOLSTM模型由輸入層、1層LSTM層和輸出層組成，輸入維數為1，輸出維數為1，灰狼種群數為30，迭代次數為500。隱藏層節點數一般依靠經驗設定，先根據輸入維數和輸出維數確定隱藏層節點數范圍，然后根據實驗選定單步預測模型的隱藏層節點數為5，輸入層節點數為5，輸出層節點數為1。

3.3單步預測

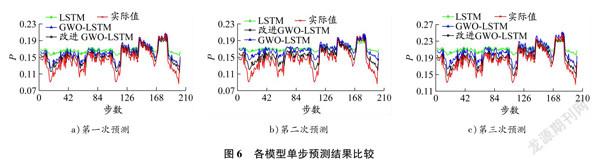
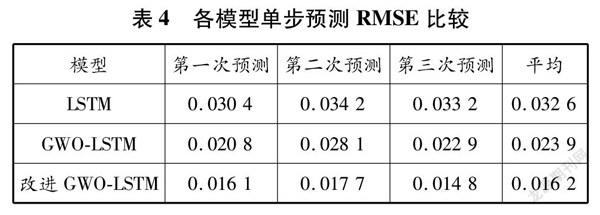
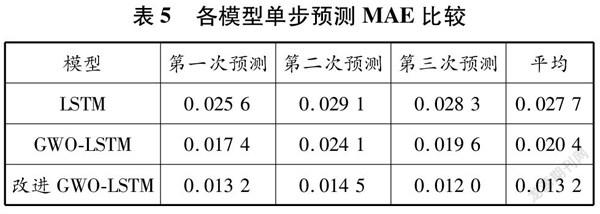
改進GWOLSTM模型、GWOLSTM模型和LSTM模型的預測結果見圖6。各模型評價指標對比見表4和5。由圖6、表4和表5可以看出，在3組實驗中，改進GWOLSTM模型的預測值曲線與真實值曲線最為吻合，其RMSE和MAE均比其他模型的低。改進GWOLSTM模型的RMSE值比LSTM模型、GWOLSTM模型的分別低了5038%、3236%。這說明改進GWOLSTM模型在船舶主機性能單步預測方面，預測效果最好，預測精度最高。

3.4多步預測

多步預測主要有兩種策略：遞歸多步策略（又叫迭代多步策略）和直接多步策略[17]。遞歸多步策略先訓練出一個單步模型，使用該模型預測下一個時間步的值，然后將該預測值作為輸入預測下一個時間步的值，逐漸循環，直到預測到第b步為止。該方法使用預測值代替真實值，因此該方法會累積預測誤差，導致預測結果的偏差較大，且該模型的性能會隨著時間的增加而急劇下降。直接多步策略是直接訓練出一個b步預測模型，該模型使用a-h至a時間步的時間序列作為輸入，預測a+1至a+b時間步的值。因此本文采取直接多步策略進行預測。先訓練一個五步預測模型，每個時間步的長度為1 min;該模型的隱藏層節點數為10，輸入層節點數為5，輸出層節點數為5。

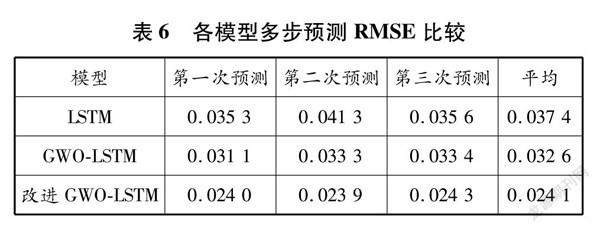
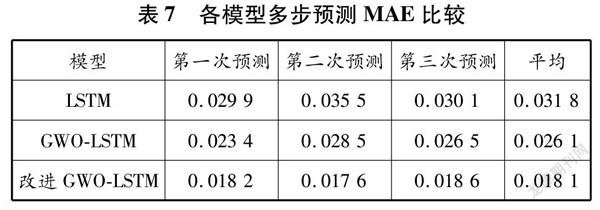
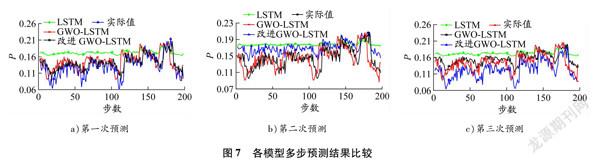
根據預測結果，計算這3種模型的評價指標，結果見表6和7。從表6、表7和圖7（各模型多步預測結果比較）可以看出，3組數據中，改進GWOLSTM模型的預測值與實際值最為貼近，其RMSE和MAE也比其他模型的低。改進GWOLSTM模型預測結果的RMSE值比LSTM模型、GWOLSTM模型的分別低了3557%、2616%。這說明改進GWOLSTM模型在船舶主機性能多步預測方面，仍具有最好的預測精度和預測效果。

4結論

為提高對船舶主機性能的預測精度，在傳統灰狼優化算法（GWO）中增加一種隨機搜索機制，用改進的GWO代替隨時間反向傳播（BPTT）算法優化長短期記憶網絡（LSTM）。分別用改進GWOLSTM模型、GWOLSTM模型和LSTM模型對船舶主機性

能進行預測，結果表明：改進GWOLSTM模型相對于GWOLSTM模型和LSTM模型，單步預測的RMSE值分別低了3236%和5038%，MAE值分別低了3513%和522%;多步預測的RMSE值分別低了2616%和3557%，MAE值分別降低了3049%和4301%。參考文獻：

[1]劉伊凡. 營運船舶主機性能退化和健康管理方法研究[D]. 大連： 大連海事大學， 2018.

[2]HOCHREITER S， SCHMIDHUBER J. Long shortterm memory[J]. Neural Computation， 1997， 9（8）： 17351780. DOI： 101162/neco.19979.81735.

[3]王子銘， 陳順懷. 基于LSTM神經網絡的船舶主機油耗實時預報[J]. 武漢理工大學學報（交通科學與工程版）， 2020， 44（5）： 923927. DOI： 103963/j.issn.20953844202005030.

[4]易文海， 高志亮. 基于LSTM神經網絡的隨機橫浪中船舶橫搖運動極短期預報[J/OL]. 武漢理工大學學報（交通科學與工程版）， 2021， 45（6）： 11131117. DOI： 103963/j.issn.20953844202106020.

[5]QIAO D S， LI P， MA G， et al. Realtime prediction of dynamic mooring lines responses with LSTM neural network model[J]. Ocean Engineering， 2021， 219： 108368. DOI： 101016/j.oceaneng.2020108368.

[6]SHI B J， SHI H J， WANG H Y. Performance prediction of marine diesel engine based on long shortterm memory network[C]∥Proceedings of the 2nd International Conference on Artificial Intelligence and Computer Science. Journal of Physics： Conference Series， 2020： 1631（1）： 012135.

[7]HU P， PAN J S， CHU S C. Improved binary grey wolf optimizer and its application for feature selection[J]. KnowledgeBased Systems， 2020， 195： 105746. DOI： 101016/j.knosys.2020105746.

[8]張新明， 姜云， 劉尚旺， 等. 灰狼與郊狼混合優化算法及其聚類優化[J/OL]. （20200326）[20210518]. 自動化學報： 117. DOI： 1016383/j.aas.c190617.

[9]劉世元， 杜潤生， 楊叔子. 利用轉速波動信號診斷內燃機失火故障的研究（1）： 診斷模型方法[J]. 內燃機學報， 2000， 18（3）： 315319. DOI： 1016236/j.cnki.nrjxb.200003020.

[10]孫秀成， 譚親明， 曾向明， 等. 基于油耗率的船用低速柴油機燃燒故障診斷[J]. 中國航海， 2018， 41（4）： 2327.

[11]張博， 張萍， 郭旭， 等. 基于試驗設計遺傳算法的船用柴油機冷卻系統多目標優化[J]. 推進技術， 2020， 41（11）： 25182529. DOI： 1013675/j.cnki.tjjs.200317.

[12]夏洪永. 船舶主機冷卻水出口溫度控制系統[J]. 艦船科學技術， 2018， 40（12）： 121123. DOI： 103404/j.issn.1672764920186A.041.

[13]LIU J Q， PAN C L， LEI F， et al. Fault prediction of bearings based on LSTM and statistical process analysis[J]. Reliability Engineering & System Safety， 2021， 214： 107646. DOI： 101016/j.ress.2021107646.

[14]MIRJALILI S， MIRJALILI S M， LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software， 2014， 69： 4661. DOI： 101016/j.advengsoft.201312007.

[15]張曉鳳， 王秀英. 灰狼優化算法研究綜述[J]. 計算機科學， 2019， 46（3）： 3038. DOI： 1011896/j.issn.1002137X.201903004.

[16]龍文， 蔡紹洪， 焦建軍， 等. 一種改進的灰狼優化算法[J]. 電子學報， 2019， 47（1）： 169175. DOI： 103969/j.issn.03722112201901022.

[17]TAIEB S B， ATIYA A F. A bias and variance analysis for multistepahead time series forecasting[J]. IEEE Transactions on Neural Networks and Learning Systems， 2016， 27（1）： 6276. DOI： 101109/TNNLS.20152411629.

（編輯賈裙平）

收稿日期： 20210511修回日期： 20210926

基金項目： 上海市科技計劃（20DZ2252300）

作者簡介： 石彪（1997—），男，山東菏澤人，碩士研究生，研究方向為輪機自動化、船舶主機性能預測，（Email）18800205042@163.com;

王海燕（1976—），男，河北平山人，副教授，博士，研究方向為輪機自動化、船舶動力裝置仿真，（Email）wanghaiyan@shmtu.edu.cn