緩沖結構長度對600 km/h磁浮列車通過隧道時的壓力波特性影響分析

張潔，王雨舸，韓帥，王璠，高廣軍，熊小慧

(1.中南大學交通運輸工程學院，軌道交通安全教育部重點實驗室，湖南長沙，410075；2.中南大學交通運輸工程學院，軌道交通安全關鍵技術國際合作聯合實驗室，湖南長沙，410075；3.中南大學交通運輸工程學院，軌道交通列車安全保障技術國家地方聯合工程研究中心，湖南長沙，410075)

作為21世紀極具競爭力的新型軌道交通方式，磁浮列車以電磁懸浮取代了原有的輪軌關系，具有速度快、舒適性好、噪聲小等優點[1-2]。迄今為止，世界上許多國家對磁浮列車進行了大量研究并取得了顯著成果。德國研發的磁吸式TR01-09系列磁浮列車在試驗線上速度達450 km/h；日本在2015 年自主研發的L0 型磁浮列車創造了603 km/h的世界磁浮載人列車行駛最高紀錄；而我國600 km/h的高速磁浮試驗樣車也在青島下線[3]，標志著我國在高速磁浮領域的重大突破。磁浮列車運行時的空氣動力學效應研究一直是高速列車重要課題。當磁浮列車從明線進入隧道時，前方空氣由于受到隧道壁面的限制無法向四周擴散，壓力驟升從而形成初始壓縮波，壓縮波以聲速向隧道出口傳播，一部分在隧道出口以微氣壓波的形式向外傳播，另一部分作為膨脹波反射至隧道入口[4]，不僅對隧道內部結構及環境產生嚴重危害，而且會影響周圍居民的生活[5]，當磁浮列車運行速度達600 km/h 時，這一空氣動力學問題變得更加突出。因此，減緩隧道空氣動力學效應對我國高速磁浮列車的發展具有重要意義。目前，人們對高速列車車/隧耦合空氣動力學研究主要集中在輪軌列車上。例如，HOWE[6]研究了隧道內壓縮波的變化曲線并提出了最大壓力梯度計算公式。YAMAMOTO[7]發現微氣壓波幅值與隧道出口壓縮波的壓力梯度呈正比關系。根據微氣壓波幅值和初始壓縮波梯度之間的關系，研究者提出了緩減微氣壓波的措施，總體來說可分為2類：一類是對高速列車及隧道結構進行優化[8-11]，即優化列車頭部形狀、頭部長細比以及隧道內部結構。周細賽等[12]對不同主型線頭部列車隧道交會氣動效應進行了研究，得到列車在隧道交會時的氣動力以及隧道壁面壓力的變化規律。但針對現有隧道和列車頭型，改進高速列車及隧道成本太高，為此，人們提出另一種減緩微氣壓波的措施，即在隧道入口增設緩沖結構[13-15]。駱建軍[16]研究了不同長度、開孔率以及形狀的緩沖結構，得到緩沖結構對壓力梯度和微氣壓波的影響規律。BELLENOUE等[17]對截面擴大型緩沖結構對壓縮波產生的影響進行研究，發現增加緩沖結構后，初始壓縮波波前被分為幾部分，并且波前數取決于緩沖結構和車頭鼻尖的長度。

相比于高速輪軌列車，磁浮列車具有更高的速度，引發的空氣動力學問題更加突出。梅元貴等[18]研究了隧道洞口初始壓縮波的空間分布特性和傳播特性，發現初始壓縮波在傳播過程中會由三維波演化為一維波。張志超等[19]研究了磁浮列車通過隧道時隧道內部氣動載荷的變化特性以及列車速度對車體表面壓力幅值的影響，馬東寶[20]分析了磁浮列車通過隧道過程中列車的氣動力變化特性與隧道壓力波的反射與疊加之間的關系。

縱觀以上研究發現，目前國內外學者采用CFD 數值模擬方法研究了600 km/h 磁浮列車通過短隧道時的初始壓縮波特性、隧道壁面壓力等，但沒有對高速磁浮列車通過中長隧道時壓力波在隧道內的傳播及耗散效應、隧道口微氣壓波進行深入研究。為此，本文以600 km/h 的磁浮列車和長度2 km的磁浮隧道為研究對象，采取三維、非定常、可壓縮N-S方程，結合k-ε湍流模型[21-23]對隧道壁面壓力及微氣壓波進行數值仿真。首先，研究磁浮列車進入無緩沖結構隧道的壓力波傳播機理及緩沖結構長度對隧道壁面壓力的影響；其次，對初始壓縮波的產生過程及壓力梯度進行分析；最后，對隧道出口微氣壓波的變化以及緩沖結構長度與微氣壓波幅值的關系進行擬合。

1 計算模型

1.1 數值仿真模型

圖1 所示為高速磁浮列車和緩沖結構幾何模型。其中，圖1(a)和圖1(c)所示為高速磁浮列車幾何模型，圖1(b)所示為隧道緩沖結構模型和橫斷面示意圖，L為緩沖結構長度。列車車高為4.2 m，寬為3.7 m，采用5 車編組，列車總長為130.7 m。借鑒中國磁浮鐵路技術標準，焦齊柱等[24]將磁浮列車隧道最優凈空面積確定為92 m2，因此，在本文數值模擬中，隧道采用單線隧道，長度為2 km，凈空面積為92 m2，高速磁浮列車橫截面積與隧道凈空面積的阻塞比為0.13。本文在隧道兩端設有長度變化范圍為50～200 m 的截面擴大型緩沖結構，橫截面積為184 m2，為隧道橫截面面積的2 倍[13]。磁浮鐵路軌道采用T型軌道梁，如圖1(d)所示，橫截面積為2.187 m2，上表面寬度為2.8 m，下表面寬度為1.94 m，高度為1.25 m。軌道梁左右兩側與磁浮列車橫向間距為11 mm，軌道梁上表面與車體底部垂向間距為20 mm。

圖1 高速磁懸浮列車幾何模型及緩沖結構Fig.1 High-speed maglev train models and tunnel hood

1.2 計算域及邊界條件

采用滑移網格技術[25-26]實現列車與地面、隧道的相對運動，即將計算域劃分為靜止區域和滑移區域2 部分。靜止區域包括隧道區域和外部計算域，而滑移區域包含整列車及軌道等需要沿運行方向運動的區域。為精確捕捉列車進入隧道時產生的壓力波特性，在隧道兩端建立長為530 m、寬為120 m、高為60 m的計算域，如圖2所示。靜止區域與滑移區域相接觸的面定義為交換面，用于信息交換，捕捉車身周圍流場的特性。隧道面、車體、地面及軌道定義為壁面。左側計算域入口、頂面及左右兩側面定義為壓力入口，右側計算域出口、頂面及左右兩側面定義為壓力遠場，具體的邊界設置如圖2所示。

圖2 計算域和邊界條件Fig.2 Computational domain and boundary conditions

計算域網格劃分采用結構化網格與非結構化網格相結合的方法，如圖3所示，在保證計算結果精度的同時，可提高計算效率。本文重點研究列車通過隧道時誘發的壓力波動，其主要與列車流線型外形、車隧阻塞比和列車運行速度等宏觀因素有關，根據文獻[27-28]，列車表面邊界層對隧道壓力波的傳播和擴散影響較小，因此，在列車、隧道壁面可不采用近壁附面層網格。若需要精確捕捉列車近壁流場特性以及氣動載荷(黏阻部分)，則必須設置近壁附面層網格，且需與空間網格保持良好過渡。在數值模擬中，本文采用URANS方法中的k-ε湍流模型求解高速磁浮列車通過隧道過程中列車周圍的湍流流場，采用SIMPLE算法求解壓力-速度耦合方程，空間離散采用二階迎風格式，時間步長為0.005 s[29]。

圖3 計算域網格分布Fig.3 Computational grid distributions

為了驗證網格精度對數值模擬結果的無關性，將計算域進行精細和中等2種精度的網格劃分。其中，中等精度的網格總數為2 080萬個，精細精度的網格總數為3 228萬個，將距離隧道入口距離分別為150 m 和1 000 m 測點的隧道壁面壓力進行對比，結果如圖4所示。從圖4可知：當網格精度處于中等和精細時，隧道壁面壓力曲線較吻合。經綜合考慮，本文數值模擬采用中等精度網格。

圖4 不同網格精度下的隧道壁面壓力時程曲線Fig.4 History of pressure on tunnel walls under different mesh precisions

1.3 隧道壁面測點布置

為研究磁浮列車通過隧道時的壓力波傳播特性以及不同緩沖結構長度對初始壓縮波的影響，在隧道壁面布置一系列測點，如圖5所示。在長為2 km的隧道上選取12個斷面，其中測點1，2，3，4，7，8，9，10，13，14，15 和16 的高度為半車高，測點5 和11 的高度為車高，而測點6 和12 位于隧道頂部。

圖5 隧道測點布置圖Fig.5 Location of measurement points on tunnel surface

1.4 計算方法驗證

為驗證本文中所采用的數值模擬方法的正確性，將數值計算結果與動模型試驗結果、理論計算結果分別進行對比，其中隧道壁面壓力波曲線、幅值采用動模型試驗結果驗證，微氣壓波幅值采用理論公式計算結果驗證。

動模型試驗在中南大學軌道交通安全教育部重點實驗室的600 km/h速度等級的磁懸浮動模型試驗平臺上完成(如圖6 所示)，該平臺獲得CMA 和CNAS(證書編號為CNAS L10220)資質認證。在動模型試驗中，采用某型3 車編組的高速磁浮列車，隧道長度為320 m，凈空面積為100 m2，模型縮比為1∶20，見圖6。距離隧道入口160 m 處隧道壁面壓力仿真結果與動模型試驗結果對比見圖7，各峰值結果見表1。由圖7和表1可以看出：本文采用的數值模擬結果與動模型試驗結果較吻合，兩者隧道壁面壓力的正峰值相對誤差為-5.30%，負峰值相對誤差為5.17%。

圖6 中南大學動模型試驗平臺Fig.6 Moving model test platform of Central South University

表1 數值仿真與動模型試驗結果對比Table 1 Results comparison between numerical simulation and moving model test

為進一步驗證本文所采用的數值模擬方法的正確性，將數值計算中得到的微氣壓波幅值與YAMAMOTO[7]提出的基于遠場和低頻方法得到的微氣壓波理論計算值進行對比，其中微氣壓波幅值計算公式如下：

式中：Pmax為微氣壓波幅值；Atu為隧道橫截面積；Ω為隧道出口處環境狀況的三維角；c0為聲速；r為測點與隧道出口處線路中心點的距離；為隧道出口處的壓縮波梯度。

數值計算的微氣壓波幅值與理論計算的微氣壓波幅值比較見表2，可知數值計算得到的微氣壓波幅值與理論計算值相對誤差較小。

表2 數值計算與理論計算得到的微氣壓波幅值對比Table 2 Comparison of micro-pressure wave amplitudes using numerical simulation and theoretical calculation

2 數值仿真結果分析

2.1 壓力波傳播效應

無緩沖結構下600 km/h磁浮列車通過隧道時，距隧道入口端1 000 m測點的隧道壁面壓力變化如圖8所示，其中，C1，C2和C3為壓縮波，E1，E2和E3 為膨脹波，H 和R 分別代表磁浮列車頭部和尾部，縱坐標X為距離隧道入口端的距離。

當磁浮列車從明線進入隧道時，前方的空氣流動受到隧道壁面的限制而被阻滯，氣流受到劇烈壓縮導致壓力驟然增大，從而產生初始壓縮波。初始壓縮波以聲速向前傳播至隧道壁面測點，從而導致壓力開始上升(見圖8 中曲線①)。初始壓縮波導致隧道壓力壁面驟升之后出現了小范圍驟降。將這一段驟降時間與車速相乘，換算成列車長度，發現對應位置為列車頭部流線型與車身過渡處。RICCO 等[30-31]通過實驗也證實了這點，其實驗主要是模擬帶有圓錐型鼻尖的圓柱以150 km/h 運行速度在長度為6.0 m 的圓管隧道模型中快速移動，其中列車長度為0.6 m，與隧道橫截面積的阻塞比β為0.147 5。

圖8 磁浮列車過隧道時壓力變化過程Fig.8 Pressure variation process of maglev train as it passes through tunnel

列車尾部進入隧道產生的膨脹波傳播至測點，導致壓力下降(見圖8 中曲線②)；初始壓縮波繼續向前傳播至隧道出口時，一部分以膨脹波的形式向隧道內反射至測點，從而使得測點壓力下降(見圖8 中曲線⑤)；膨脹波在隧道出口以壓縮波的形式返回至測點，壓力上升(見圖8 中⑥)。當磁浮列車的頭部經過測點時，隧道壁面壓力驟降(見圖8中③)；當尾部經過測點時，測點壓力驟升(見圖8中④)，其主要原因是列車誘導空氣流動，使氣流速度突然發生變化，從而使測點壓力也發生變化。由此可知，當壓縮波經過時，測點壓力上升；當膨脹波經過時，測點壓力下降。

2.2 隧道壁面壓力

圖9所示為磁浮列車以600 km/h通過無緩沖結構的隧道時，距離隧道入口150 m處測點4，5和6的隧道壁面壓力變化曲線。由圖9可知：在同一橫斷面處，不同高度測點的隧道壁面壓力變化曲線基本重合，最大壁面壓力幅值比最小壁面幅值壓力僅大1.67%，因此，在隧道內壓力波傳遞呈現較強的一維特性，與文獻[18]中的研究成果保持一致。

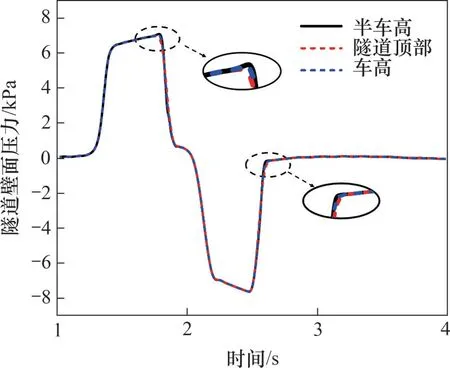
圖9 不同壁面測點壓力時間歷程Fig.9 Time history of pressure of measuring points on tunnel walls

距離隧道入口140 m處緩沖結構長度對隧道壁面壓力變化的影響如圖10 所示，其中，緩沖結構長度L分別取50，80，100，150和200 m。由圖10可知：無緩沖結構時測點的壓力曲線波動較小；當在隧道口兩端增設緩沖結構后，壓力變化波動較大，其主要原因是從緩沖結構末端到隧道入口處存在橫斷面積突變，壓縮波傳播至該處時會發生明顯的反射現象，導致增加緩沖結構后隧道內的壓力發生復雜變化。在增加緩沖結構后，隧道壁面壓力上升過程被分為2個階段：第一階段，磁浮列車駛入緩沖結構時產生的壓縮波使得壓力上升，當列車駛入一段時間后，壓力趨于平穩狀態，平穩時間隨緩沖結構長度增大而增加；第二階段，磁浮列車從緩沖結構駛入隧道入口，再次產生的壓縮波使壓力上升。將有、無緩沖結構下的隧道壁面壓力進行對比可以發現，緩沖結構并未改變壁面壓力達到峰值的時間，但由于緩沖結構存在，隧道壁面測點壓力開始上升的時間提前。

圖10 緩沖結構長度對隧道壁面壓力的影響Fig.10 Influence of hood length on pressure curves on tunnel walls

2.3 初始壓縮波和壓力梯度

當磁浮列車由明線進入隧道時會產生壓縮波，稱為初始壓縮波。據文獻[13]可知，微氣壓波幅值與隧道內初始壓縮波梯度成正比，因此，減緩微氣壓波強度的有效方法是減小初始壓縮波梯度。

圖11 所示為距離隧道入口100，1 000 和1 800 m 處的初始壓縮波壓力及壓力梯度變化示意圖(其中，L為緩沖結構長度)。從圖11(a)，(c)和(e)可以看出：增設緩沖結構后，壓縮波的壓力上升階段被分為p1 和p2 共2 部分[17]，其中，p1 代表磁浮列車由明線進入緩沖結構時產生的壓縮波引起的壓力波動，p2 代表磁浮列車從緩沖結構進入隧道時產生的壓縮波引起的壓力波動。本文中，以列車到達隧道入口的時間為基準點來研究，故不同緩沖結構長度下p2 的壓力時程曲線重合，壓縮波達到峰值時間相同，而p1和p2達到峰值之間的時間差主要是緩沖結構長度不同所致。在距離隧道入口100 m處，5種長度緩沖結構下p1的峰值基本相同，相對誤差絕對值在5%以內，只是達到峰值的時間不同。

圖11 不同緩沖結構長度對初始壓縮波及梯度的影響規律Fig.11 Influence of hood length on initial compression wave and corresponding pressure gradient

當測點距離隧道入口1 000 m 及1 800 m 時，相比于其他長度的緩沖結構，當緩沖結構長度為50 m時，p1較大，且在距離隧道入口1 800 m處的壓力上升的2個階段相合并，這是因為由于緩沖結構長度較短，且磁浮列車運行速度快，產生的2個壓縮波的時間間隔較短，而后波的傳播速度大于前波的傳播速度，故2個階段產生的壓縮波在傳播過程中逐漸融合成為1個壓縮波，使得在隧道出口時緩沖結構長度為50 m 的壓力梯度相較于其他長度的壓力梯度較大，這導致在緩沖結構長度為50 m 時，隧道出口的微氣壓波幅值較其他緩沖結構長度時較大。

通過初始壓縮波的第1次壓力上升階段可確定壓力梯度幅值[6]，因此，在考慮初始壓縮波的壓力梯度時僅對p1 進行分析。不同緩沖結構長度下距離隧道入口100，1 000和1 800 m處的初始壓縮波梯度幅值如表3所示。從表3可見：當緩沖結構長度一定時，初始壓縮波梯度幅值隨著距隧道入口端距離的增大而增大[32]，其原因主要是壓縮波在傳播過程中，波后的傳播速度大于波前的傳播速度，隨著傳播距離增加，其壓力梯度也增大，導致出現激化現象；對于不同長度的緩沖結構，當緩沖結構長度小于100 m時，隨著長度增加，測點的壓力梯度幅值不斷減小，最大降幅為51.6%；當100 m＜L＜200 m 時，隨著緩沖結構長度增加，初始壓縮波梯度幅值基本保持不變。因此，針對600 km/h的磁浮列車，緩沖結構長度為100 m即可達到最大緩解效果。

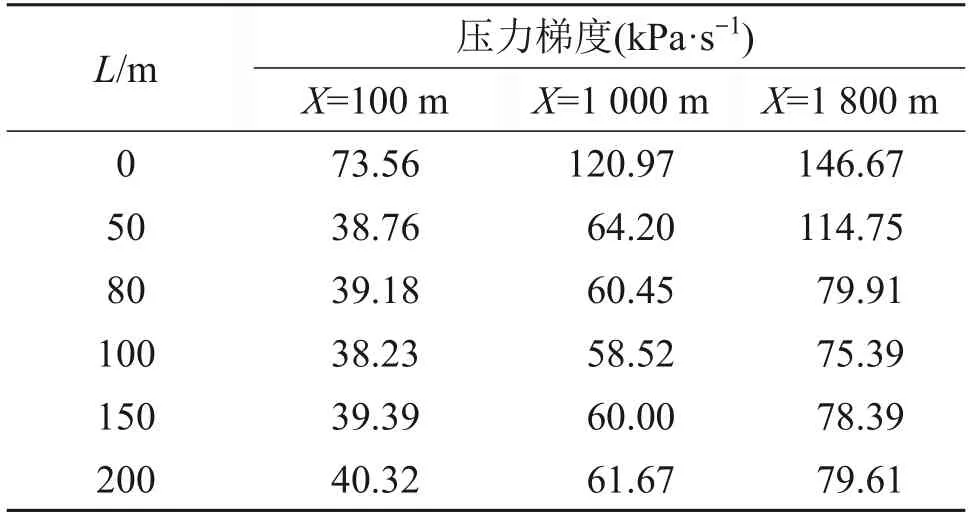
表3 不同緩沖結構長度的初始壓縮波壓力梯度Table 3 Pressure gradients of initial compression waves under different hood lengths

2.4 微氣壓波

磁浮列車進入隧道產生的初始壓縮波在隧道出口會分為2部分：一部分以膨脹波的形式向隧道內傳播，另一部分以脈沖波的形式輻射出去，在隧道出口處發出強烈的空氣爆鳴聲，產生噪聲污染，這一脈沖壓力波稱為隧道出口微氣壓波[6]。根據隧道洞口微氣壓波幅值要求，設置緩沖結構的條件如下：一是在距洞口外50 m 內無建筑物，20 m處的微氣壓波幅值大于50 Pa；二是距洞口50 m內有建筑物，建筑物處的微氣壓波幅值大于20 Pa。因此，本文對距離隧道出口20 m和50 m的微氣壓波進行研究。

不同緩沖結構長度下距隧道出口端20 m 和50 m處的微氣壓波幅值分別見表4和表5。為便于觀察，將微氣壓波幅值與緩沖結構長度繪制成折線圖，如圖12所示。由圖12可知：在隧道進出口安裝緩沖結構可有效降低微氣壓波幅值；在距隧道出口端20 m 和50 m 處，緩沖結構長度為100 m時的緩解率達到最高，分別為60.0%和58.9%；當緩沖結構長度小于100 m時，隨著緩沖結構長度增加，微氣壓波幅值逐漸下降；當緩沖結構長度大于100 m時，微氣壓波幅值呈現小幅度增長趨勢。

圖12 同緩沖結構長度下的微氣壓波幅值Fig.12 Amplitudes of micro-pressure waves at different hood lengths

表4 隧道出口20 m處的微氣壓波幅值Table 4 Amplitudes of micro-pressure wave at distance of 20 m from the exit of tunnel

表5 隧道出口50 m處的微氣壓波幅值Table 5 Amplitudes of micro-pressure wave at distance of 50 m from the exit of tunnel

不同長度緩沖結構下微氣壓波幅值與距隧道出口距離擬合曲線如圖13 所示，擬合方程和相關系數如表6所示。從圖13和表6可見：微氣壓波幅值隨著距隧道出口距離增加而逐漸衰減；當緩沖結構為50 m 時，微氣壓波幅值較高，其主要原因是當緩沖結構長度為50 m 時，壓力梯度相較于其他長度緩沖結構的壓力梯度較大，因此，微氣壓波幅值也較大；對于其他長度的緩沖結構，在微氣壓波傳遞過程中，幅值與距隧道出口距離的變化規律相同。因此，分別對緩沖結構長度為50，80～200 m 的微氣壓波幅值和隧道出口距離的關系進行冪函數擬合，相關系數分別為0.993 和0.994。據文獻[33]可知，高速輪軌列車的微氣壓波幅值與距隧道出口端距離的1次方呈反比，而當磁浮列車速度更高時，微氣壓波幅值近似與距隧道出口端距離的0.85次方呈反比。

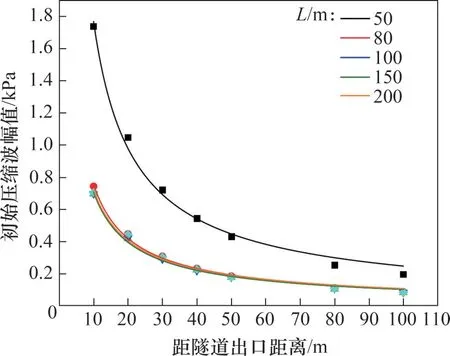
圖13 不同距離的微氣壓波幅值擬合曲線Fig.13 Fitting curves of amplitudes of micro-pressure waves at different positions

表6 不同位置的微氣壓波幅值擬合關系式Table 6 Fitting relationships of amplitudes of micropressure waves at different positions

3 結論

1)隨著磁浮列車速度提高，車隧耦合效應更加突出。在壓力波傳播過程中，波后的速度大于波前的速度，導致初始壓縮波被激化，壓力梯度沿隧道逐漸增加。

2)增加緩沖結構可以有效降低微氣壓波幅值。對比不同長度緩沖結構的仿真結果可知，長度為100 m 的緩沖結構是最有效的，與無緩沖結構相比，隧道出口20 m處的微氣壓波幅值降低60%。

3)隨著緩沖結構長度增加，初始壓縮波的壓力梯度逐漸減小；當長度超過100 m時，緩解效果基本保持不變。