輪軌型面匹配對鋼軌亞表面抗疲勞裂紋擴展影響

方修洋，張昊楠，馬東文

(西南交通大學機械工程學院，四川成都，610031)

隨著我國鐵路運輸朝著高速重載的方向迅猛發展，鐵路輪軌間承受著愈加嚴酷的滾動、滑動以及沖擊載荷的作用，這給鐵路安全運輸帶來了極大挑戰。在嚴酷服役載荷作用下，輪軌表面及亞表面常常會產生一定的疲勞裂紋[1-2]。表面裂紋通常可以通過輪軌間的磨損得以消除，而亞表面裂紋往往會成為輪軌的薄弱區域[3]。因此，精確評估輪軌亞表面抗疲勞裂紋擴展能力具有重要理論與工程意義。

針對鋼軌亞表面抗疲勞裂紋擴展，國內外學者已開展了一些有意義的研究工作。MASOUDI NEJAD等[4]利用FRANC3D建立了鋼軌表面裂紋模型，研究了加載方向與輪軌磨耗對鋼軌疲勞裂紋擴展的影響，發現鋼軌疲勞裂紋擴展壽命將隨著接觸應力增加而減小，輪軌接觸斑的大小直接影響鋼軌所受應力以及其疲勞壽命，且與橫向裂紋相比，縱向裂紋對鋼軌的疲勞壽命影響更大。鋼軌磨耗所產生的疲勞累積塑性變形，對鋼軌表面和亞表面均會造成不同程度的損傷，磨耗對表面的損傷尤其顯著，輪軌循環接觸載荷產生的剪切應力將導致鋼軌亞表面的微觀組織在剪切方向上被拉長斷裂且沿剪切方向排列，疲勞裂紋由此萌生[5-7]。BONNIOT等[8]對軌道鋼試樣進行了非對稱四點彎曲試驗，研究剪切載荷作用下裂紋擴展特性，獲取了Ⅱ型、Ⅲ型復合加載下的裂紋擴展門檻值，研究發現在足夠高的加載范圍內，會導致裂紋共面剪切型擴展，并且在主裂紋面方向上會誘發形成次生I型分支裂紋，利用局部應力應變法疲勞損傷模型證明了其合理性，預測了裂紋尖端擴展路徑與擴展速率。徐慧等[9-10]通過理論推導了三維復合型裂紋等效應力強度因子計算公式，并應用有限元數值計算與解析解對比驗證了復合裂應力強度因子計算方法的有效性，并通過復合加載試驗發現I型裂紋占主導地位的降低會使得試件的疲勞壽命顯著增加。

盡管針對鋼軌抗疲勞裂紋擴展已開展一些有意義的研究，但復雜輪滾接觸載荷作用下已損傷鋼軌剩余壽命評估理論仍未形成，而輪軌踏面匹配對鋼軌抗疲勞裂紋擴展能力的影響是進行復雜輪滾接觸載荷作用下已損傷鋼軌剩余壽命評估的基礎[11]。因此，本文作者在已有研究基礎上，選取不同輪軌磨耗模型，結合有限元方法計算鋼軌直線運行工況和曲線運行工況下的等效應力分布，并在模型中引入初始裂紋進行疲勞壽命計算，深入探討輪軌型面匹配形式對鋼軌亞表面疲勞裂紋擴展能力的影響。研究工作為亞表面存在一定損傷鋼軌剩余壽命評估提供了理論依據，也為不同輪軌匹配下鋼軌合理維修周期的制定提供了一定技術支撐。

1 研究方法

1.1 輪軌選型

列車實際運行中，線路上最普遍的輪軌匹配狀態是磨耗未到限車輪與磨耗未到限鋼軌匹配；車輪磨耗到限后進廠鏇修，恢復磨耗型面至標準型面后再返到線路繼續服役；而對于動車組列車，由于軸重輕的特點，標準車輪與標準鋼軌匹配時，輪軌型面磨損也會經歷一段較長時間。將標準型面的車輪鋼軌定義為新輪新軌，磨耗狀態輪軌定義為磨耗輪磨耗軌。本文重點分析新輪新軌、新輪磨耗軌、磨耗輪磨耗軌這3種典型的輪軌型面匹配方式下鋼軌的應力狀態與裂紋擴展特性。

直線運行工況下，輪軌型面選擇運行相同里程(15 萬km)時的磨耗狀態型面[12-13]；曲線運行工況下，新輪新軌匹配運行初期，鋼軌處于劇烈磨耗階段，當鋼軌磨耗量超過5 mm后，輪軌接觸狀態變化趨于平緩，鋼軌處于穩定磨耗階段[14]。此外，在曲線運行路段，同一段鋼軌在不同位置的鋼軌磨耗程度也存在很大差異，從緩和曲線到圓曲線，隨著曲率半徑的增大，鋼軌磨耗程度依次嚴重，圓曲線處鋼軌磨耗最為嚴重，磨耗量也最大；因此，本文曲線運行工況鋼軌磨耗型面選擇圓曲線處磨耗量相對較大的實測型面，磨耗狀態車輪型面選擇磨耗穩定期型面[15]。

標準輪軌型面采用LMA-60N，整體輪軌有限元模型如圖1(a)所示，根據直線段與曲線段輪軌磨耗后實測型面分別建立直線運行和曲線運行2種工況下新輪新軌、新輪磨耗軌、磨耗輪磨耗軌6組不同匹配型面的輪軌接觸有限元模型如圖1(b)所示。車輪滾動圓直徑為920 m，軌底坡設為1∶40。輪軌模型采用Solid185單元，劃分六面體網格在進行網格劃分時對輪軌關鍵局部部位進行細化處理，輪軌接觸部位采用0.5 mm 網格，踏面以下劃分15層，中間用1 mm網格過渡，再依次使用網格尺寸2，4 和8 mm 的單元過渡。輪軌接觸部位采用CONTA173-TARGE170 面-面接觸單元。曲線運行工況下車輪與鋼軌接觸位置采用輪軌配合最優點原則進行確定，并考慮實際情況下車輪的橫移量[13]。

圖1 輪軌有限元模型Fig.1 Finite element model of wheel-rail

1.2 材料與邊界條件

輪軌材料采用雙線性彈塑性本構模型，材料的具體參數如表1所示。

表1 輪軌材料參數Table 1 Material properties of wheel-rail

載荷條件為：直線運行工況下，車輪所受載荷只有垂向軸重P，將垂向載荷FV施加于車輪中心處，載荷FV取軸重的一半；曲線運行工況下，根據國際鐵路聯盟標準UIC510-5 和歐洲標準EN13979-1，除了垂向載荷外，車輪還受橫向載荷Fh的作用，Fh=αP，α為橫向載荷系數，對于非導向輪對，α取0.6。

約束條件為：鋼軌底部全約束，兩端施加對稱約束；對于車輪，約束車輪中心X方向、Z方向平動位移，Y方向、Z方向轉動位移。

1.3 疲勞裂紋擴展模型

Von Mises 應力是基于剪切應變能的一種等效應力，其最大值處最容易發生屈服破壞，也最容易萌生疲勞裂紋。因此，基于Von Mises 準則，在鋼軌內部Mises應力最大處引入初始裂紋，裂紋形狀設為圓形，裂紋半徑為1 mm，裂紋面平行于水平面(XOZ)。

對于多軸載荷下的復合型裂紋擴展準則，本文采用最大能量釋放率準則，該準則能確定多軸應力狀態下裂紋尖端任意方向上的能量釋放率，且與實驗結果吻合度高[16]；應力強度因子利用M積分計算[17]；基于等效應力強度因子Keq[18]預測多軸載荷下疲勞裂紋擴展速率：

其中，三維復合裂紋等效應力強度因子[19]計算公式為

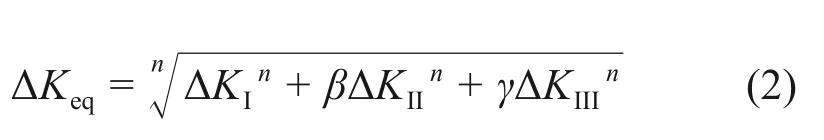
式中：β，γ和n為權重因子，通過理論推導，本文取β=γ=1，n=2[9]；C和m為材料常數，參考U71Mn鋼的疲勞裂紋擴展速率曲線擬合參數C=4.597×10-13，m=2.88[20]。

疲勞裂紋擴展壽命通過式(1)積分得到。為研究輪軌磨耗狀態下不同型面匹配時鋼軌亞表面裂紋擴展壽命和擴展速率變化規律，基于鋼軌表面及內部Von Mises應力云圖(圖2)，在不同輪軌型面匹配條件下的鋼軌亞表面不同深度Von Mises 應力最大處插入圓形初始裂紋，裂紋半徑為1 mm，裂紋面與水平面平行，初始裂紋引入設置如圖1(c)所示，分別計算其疲勞裂紋擴展壽命和擴展速率。

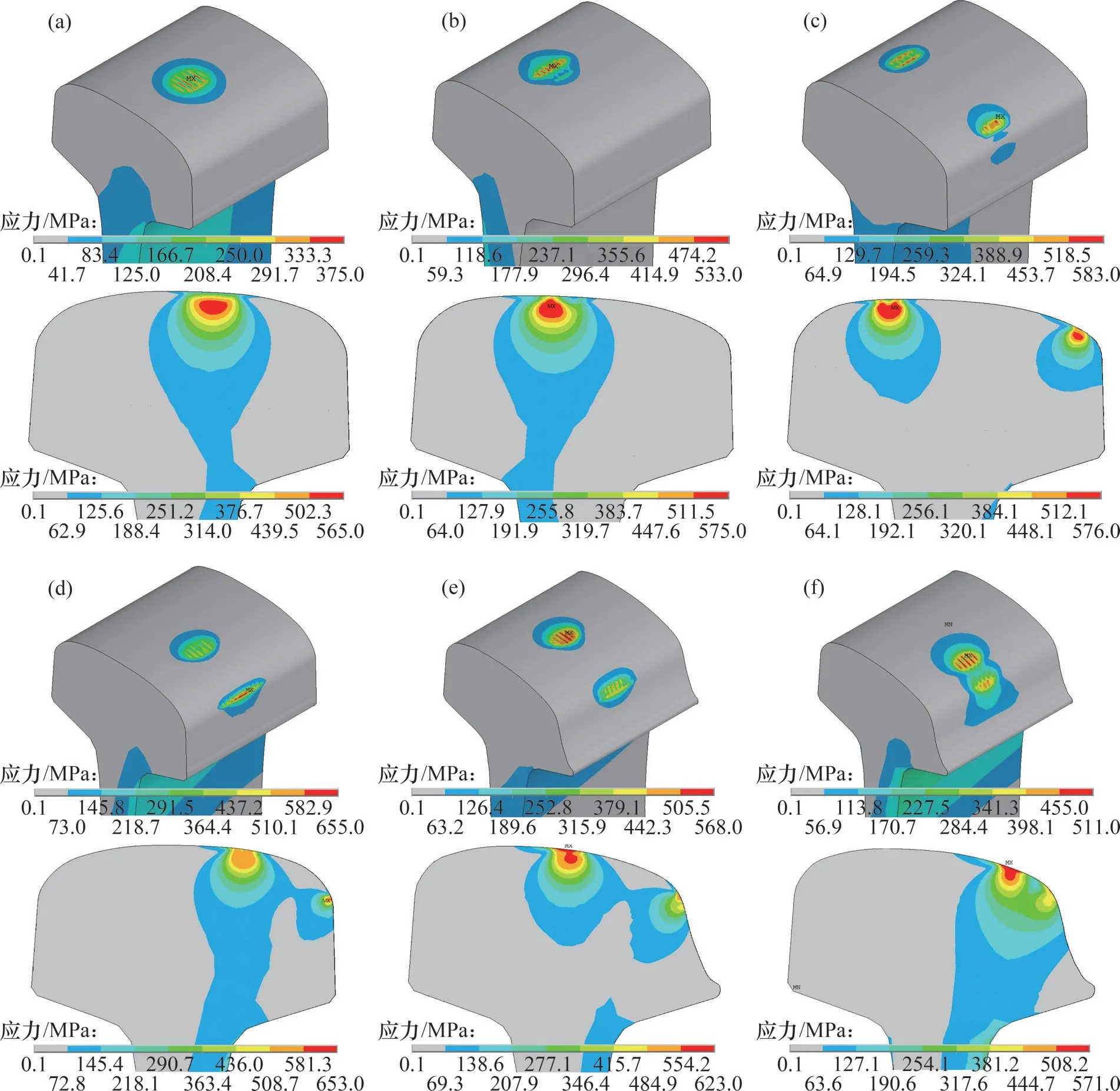
圖2 鋼軌表面及內部Von Mises應力云圖Fig.2 Von Mises stress contour of rail surface and internal

2 結果與討論

2.1 鋼軌應力場分布

圖2(a)～(c)和圖3(a)所示為直線運行工況下不同輪軌型面匹配時鋼軌表面和內部Von Mises 應力分布。由圖2(a)～(c)和圖3(a)可知：新輪新軌匹配時，鋼軌亞表面Mises 應力最大值為565 MPa，位于軌面以下3 mm處，新輪磨耗軌匹配、磨耗輪磨耗軌匹配時，鋼軌亞表面Mises應力最大值分別為575 MPa 和576 MPa，位于軌面以下2 mm 處。鋼軌磨耗后，輪軌接觸點位置和鋼軌次表面最大等效應力深度均發生了變化，磨耗輪與磨耗軌匹配時，軌面出現兩點接觸，鋼軌內側軌距角附近也出現了應力集中，加速鋼軌內側磨耗，鋼軌亞表面最大等效應力深度也更靠近鋼軌表面位置，容易誘發裂紋萌生或踏面剝離。

圖2(d)～(f)和圖3(b)所示為曲線運行工況下3組不同輪軌型面匹配時鋼軌Von Mises 應力沿鋼軌踏面深度方向分布。從圖2(d)～(f)和圖3(b)可知：鋼軌分別為新輪新軌匹配、新輪磨耗軌匹配、磨耗輪磨耗軌匹配時，鋼軌亞表面最大Mises應力深度均在2 mm 處，最大值分別為563，561 和533 MPa，比較可知，曲線運行工況下，磨耗輪與磨耗軌匹配時，鋼軌亞表面最大等效應力最低；曲線運行工況下，鋼軌表面應力均明顯增大，且磨耗狀態鋼軌與車輪匹配運行時，鋼軌表面應力大于新輪新軌匹配時的表面應力。

圖3 鋼軌內部Von Mises應力隨鋼軌踏面深度的變化Fig.3 Variation of Von Mises stress with depth of rail tread

圖4所示為直線運行工況下3種輪軌型面匹配下輪軌接觸壓力云圖。由圖4可知，新輪新軌匹配時，接觸斑呈現出較規則的橢圓形，接觸壓力相對較小且分布均勻；新輪磨耗軌匹配時，接觸壓力最大值區域沿鋼軌運行方向呈細長條形，出現明顯應力集中，接觸應力達到了1 347 MPa；磨耗輪磨耗軌匹配時，輪軌接觸位置出現了兩點接觸，除了軌面外，軌距角區域也與車輪輪緣發生了接觸，接觸壓力最大值區域集中分布，接觸面積小，接觸應力大，接觸應力最大值為1 210 MPa。

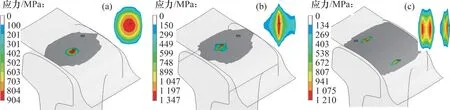
圖4 直線運行工況輪軌接觸壓力云圖Fig.4 Wheel-rail contact pressure contour under straight line service condition

圖5所示為曲線運行工況下3種輪軌型面匹配下輪軌接觸壓力云圖。由圖5可知：新輪新軌匹配時，輪軌兩點接觸，鋼軌軌距角處發生嚴重的應力集中，接觸壓力達到1 300 MPa；新輪磨耗軌匹配時，輪軌間也是兩點接觸，但是鋼軌軌距角處應力較低，軌頂面接觸區域的應力也比新輪新軌匹配時的顯著降低，最大接觸壓力為950 MPa；磨耗輪磨耗軌匹配時，輪軌共形接觸，接觸面積增大，接觸壓力進一步降低且分布均勻，最大接觸壓力為877 MPa。

圖5 曲線運行工況輪軌接觸壓力云圖Fig.5 Wheel-rail contact pressure contour under curve service condition

綜上所述，車輪在曲線段的磨耗比直線段的磨耗嚴重，因此，磨耗輪磨耗軌匹配時，曲線段配合效果優于直線段配合效果。直線運行工況下，新輪新軌匹配時，接觸斑呈現出較規則的橢圓形，接觸壓力分布均勻且相比最小，鋼軌內部等效應力值也相對最低，匹配效果最好；曲線運行工況下，穩定期的磨耗輪磨耗軌匹配時，輪軌間形成共形接觸，接觸面積大，接觸壓力小，鋼軌次表面等效應力值最低，匹配效果最好。

2.2 不同輪軌型面匹配下鋼軌抗疲勞裂紋擴展能力

選其中一種輪軌匹配工況，對鋼軌亞表面裂紋進行分析。圖6所示為曲線運行工況下磨耗輪磨耗軌匹配下輪軌橫截面Mises 應力云圖。從圖6 可見：裂尖區域應力達到900 MPa以上，裂尖等效應力達到1 931 MPa，這是裂尖應力集中導致的，說明應力已經不適用于評估裂尖應力場的強弱；疲勞裂紋擴展過程中形成了以初始裂紋面為裂紋源核心的疲勞滑移帶，裂紋面角度波動較小，始終與初始裂紋面接近共平面擴展，且在沿鋼軌外側X軸方向擴展的最快，裂紋面兩側Z軸方向擴展較快，形成了橢圓形裂紋形貌。以裂紋擴展最快路徑方向為基準，將裂紋從初始裂紋擴展至當前裂紋劃分為4 個裂紋面(step1～step4)進行應力強度因子的對比計算，初始裂紋為step1，如圖6(b)所示。

圖6 曲線運行工況磨耗輪磨耗軌匹配Mises應力云圖Fig.6 Von Mises stress contour of matching worn wheel with worn rail under curve service condition

圖7所示為4個裂紋面Step1～Step4的應力強度因子(SIF)分布。在裂紋擴展最快的路徑上，初始裂紋從0 mm 擴展至2.5 mm 過程中，Ⅱ型SIF 連續增大，I型、Ⅲ型SIF均為負值且接近于0，說明在該路徑下，I型、Ⅲ型SIF對裂紋擴展均沒有貢獻。在該路徑下，疲勞裂紋每一步擴展時裂紋面尖端始終受到X軸方向沿鋼軌外側的剪切應力作用，使得裂紋面發生滑移擴展。裂紋擴展階段Mises應力云圖變化如圖8所示。圖8也表明了裂紋面發生滑移擴展的過程。裂紋擴展過程中，裂尖左端的奇異等效應力始終最大，裂紋擴展速率最大。

圖7 裂紋擴展最快路徑上應力強度因子分布Fig.7 Variation of SIF on the fastest crack propagation path

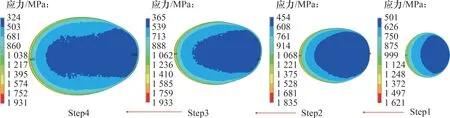
圖8 裂紋擴展階段Mises應力云圖變化Fig.8 Von Mises stress contour under different crack propagation stages

圖9 所示為裂紋擴展過程中整個裂尖的SIF 分布，在整個擴展歷程中，I型SIF 始終為負值且接近于0，裂紋不產生張開位移，Ⅱ型SIF 最大值均分布在裂尖歸一化距離0.5處，此區域裂尖產生滑動位移，進行滑移擴展，Ⅲ型SIF最大值與最小值均分布在歸一化距離0.25與0.75處，在這2個微區域裂尖產生撕開位移，進行撕裂擴展，且Ⅲ型最大值均小于Ⅱ型最大值，說明鋼軌亞表面裂紋擴展主要是剪切應力引起的Ⅱ型、Ⅲ型復合裂紋擴展，I 型SIF 對其擴展沒有貢獻。計算結果與DYLEWSKI等[6,8]的試驗結果吻合較好。

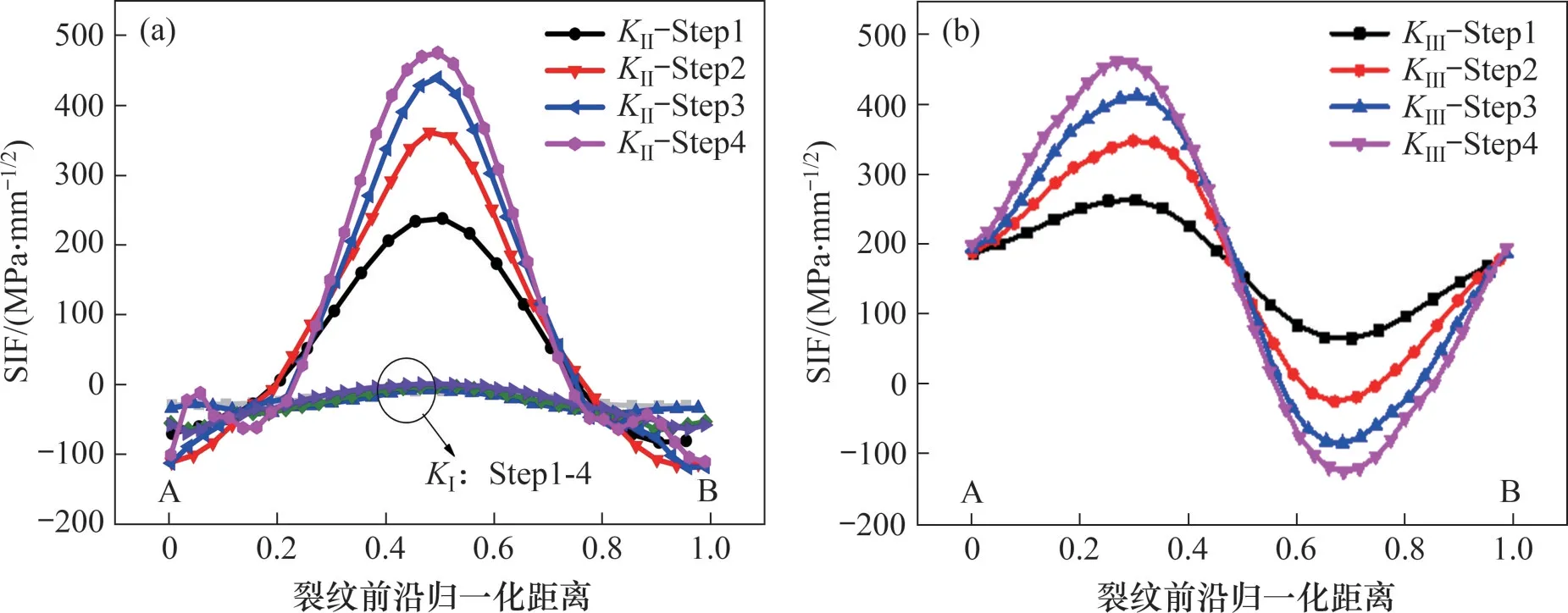
圖9 裂紋尖端應力強度因子(SIF)分布Fig.9 Distribution of SIF at fatigue crack tip

在裂紋擴展最快的路徑上計算擴展量對應的循環次數，以裂紋擴展量達到2 mm 左右為基準，以鋼軌亞表面為研究對象，直線運行工況和曲線運行工況下，3種輪軌型面匹配時鋼軌亞表面疲勞裂紋擴展壽命曲線(a-N曲線)如圖10所示。由圖10可知：直線運行工況下，新輪新軌匹配時，鋼軌亞表面疲勞裂紋擴展壽命達到了1.7×107次，高于新輪磨耗軌匹配時的1.2×107次和磨耗輪磨耗軌匹配時的2.5×106次。曲線運行工況下，新輪新軌、新輪磨耗軌匹配下鋼軌次表面疲勞裂紋擴展壽命相近，分別為5.6×106次和4.8×106次，而磨耗輪磨耗軌匹配下鋼軌亞表面裂紋擴展壽命達到了8.1×106次。

根據圖10 所示的裂紋擴展壽命與擴展量的關系，計算裂紋擴展量與對應的擴展循環次數比值Δa/ΔN，再根據da/dN≈Δa/ΔN[21]，得到裂紋擴展速率da/dN與等效應力強度因子ΔKeq的關系。2 種工況下，基于圖6(b)在裂紋指定擴展路徑下da/dN與ΔKeq(裂紋擴展驅動力)的關系如圖11所示。從圖11可知，3種匹配方式下，裂紋起始擴展驅動力ΔKeq越大，裂紋平均擴展速率越快。在直線運行工況下，新輪新軌、新輪磨耗軌匹配時，裂紋擴展速率慢，鋼軌亞表面裂紋起始擴展驅動力ΔKeq相近，裂紋擴展速率曲線基本一致，說明平均裂紋擴展速率接近，且新輪磨耗軌匹配下裂紋擴展略快一些；磨耗輪磨耗軌匹配時，鋼軌亞表面裂紋起始擴展驅動力ΔKeq顯著增大，擴展速率也相對最快。新輪新軌匹配和新輪磨耗軌匹配時鋼軌亞表面裂紋擴展速率相近，跟磨耗輪磨耗軌匹配時差距很大。

圖10 a-N曲線圖Fig.10 Variation of crack propagation cycles with crack length

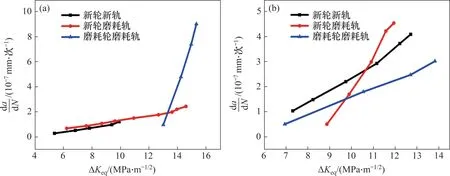
圖11 鋼軌亞表面裂紋擴展速率隨等效應力強度因子的變化Fig.11 Variation of subsurface crack growth rate of rail with equivalent stress intensity factor

在曲線運行工況下，新輪新軌、新輪磨耗軌匹配時裂紋擴展速率快，新輪磨耗軌匹配時鋼軌亞表面裂紋起始擴展驅動力ΔKeq大，裂紋擴展速率較快；磨耗輪磨耗軌匹配時，鋼軌亞表面裂紋起始擴展驅動力ΔKeq最小，平均擴展速率也相對最慢。新輪新軌匹配和新輪磨耗軌匹配時鋼軌亞表面裂紋擴展速率相近，與磨耗輪磨耗軌匹配比較，擴展速率差距較大。

2.3 輪軌型面匹配對鋼軌亞表面裂紋擴展特性的影響分析

當鋼軌亞表面由于各種原因萌生裂紋缺陷時，在輪軌磨耗及滾動接觸循環載荷下裂紋會逐漸擴展，表面裂紋也會沿深度方向擴展[7]，當表面裂紋與亞表面裂紋相遇融合時，極易導致軌面剝離、掉塊。

直線運行工況下，新輪新軌匹配接觸運行時，輪軌接觸斑形狀規則，接觸面積大，接觸壓力分布均勻，使得鋼軌次表面等效應力相對較低，等效應力最大值位置較深(距表面3 mm)，裂紋擴展速率慢，剩余壽命長；結合圖4 可知，新輪磨耗軌、磨耗輪磨耗軌匹配運行時，由于輪軌磨耗程度不同，即使磨耗輪與磨耗軌匹配運行時，型面配合效果也很差，使得接觸壓力最大值區域分布集中，接觸面積小，應力集中嚴重，局部接觸壓力顯著增大，鋼軌亞表面等效應力最大值也相對更大，其深度也距離表面更近(距表面2 mm)，在此應力場下，裂紋擴展速率快，剩余壽命短。

曲線運行工況下，隨著鋼軌磨耗量的增大，輪軌匹配效果也會逐漸變好，當磨耗量達到一定階段時，鋼軌磨耗將趨于穩定階段，該階段的輪軌匹配效果最好，等效應力最低。從圖4和圖5可見，曲線運行工況下，由于存在離心力產生的橫向載荷，輪軌接觸位置均在鋼軌內側的軌距角附近區域，橫向載荷引起的橫向切應力會促進裂紋面滑移擴展；新輪新軌匹配、新輪磨耗軌匹配時均形成兩點接觸，隨著輪軌磨耗，穩定期的磨耗輪磨耗軌匹配時，輪軌間形成了共形接觸。共形接觸下，接觸斑面積大，接觸壓力分布均勻，接觸壓力小，鋼軌亞表面的等效應力也相對更低，進而鋼軌不易磨損，當出現初始裂紋缺陷時，其裂紋擴展速率也相對較慢，剩余壽命更長。

3 結論

1)距鋼軌表面2～3 mm處等效應力最大，易引起鋼軌剝離掉塊；直線運行工況下，新輪新軌匹配時鋼軌等效應力最大值發在鋼軌內部亞表面(距表面3 mm處)，隨著輪軌表面磨損，磨耗軌等效應力最大值逐漸轉移至表面；曲線運行工況鋼軌等效應力最大值發生在鋼軌表面。

2)距鋼軌表面2～3 mm處的疲勞裂紋擴展是剪切應力引起的Ⅱ型、Ⅲ型共面剪切型擴展，且以Ⅱ型滑移擴展為主導。

3)直線運行工況下，新輪新軌匹配時鋼軌亞表面等效應力最低，裂紋擴展驅動力小，裂紋擴展速率最慢，擴展壽命最長，抗疲勞裂紋擴展能力最強；曲線運行工況下，磨耗輪與磨耗軌匹配時鋼軌亞表面應力最低，裂紋擴展速率最慢，擴展壽命最長，抗疲勞裂紋擴展能力最好。