基于HHT算法的公路瀝青老化前后流變特性提取方法

楊 博

（開封市建筑工程質量監督站, 河南開封475004）

希爾伯特-黃變換(Hilbert-Huang Transform,HHT)算法是1998年時海外華裔學者研究提出的,該算法是全新模式的經驗模態分解時頻分析法,在HHT算法中,不僅具備Hilbert譜的定理,還包含Hilbert譜分析,采用該算法能夠有效提取信號的時域與頻域,同時在提取過程中,具備較高的自適應性[1-2],十分適合對非平穩信號甚至是流變信號進行分析。

在路面膠結材料的使用中,瀝青是使用最為廣泛的材料之一[3-4]。瀝青經過生產、儲存以及路面鋪設等一系列服役過程中,由于受到天氣、溫度、行車環境等外力影響[5],均存在老化現象,以至于瀝青自身特性出現損耗。通常情況下,瀝青的老化程度與路面承受性存在密切關聯[6-8],因此,研究瀝青老化前后的流變情況能夠有效分析路面的承受能力。較多學者針對瀝青流變狀況進行研究,例如：肖慶一等[9]研究熱老化作用下廢機油改性瀝青高溫流變性能；楊仲尼等[10]研究納米碳酸鈣對道路石油瀝青流變特性影響,但對實際路面的瀝青變化情況研究精準性較差。因此,本文采用HHT算法,通過模擬分析與實際試驗相結合的形式,提取了公路瀝青老化前后流變特性。

1 公路瀝青老化前后流變特性提取方法分析

1.1 試驗材料

采用蘭煉-90(LAL)、埃索-90(ESSO)這2種公路建設使用最為廣泛的基質瀝青進行老化試驗,這兩種瀝青的基本性能指標見表1。

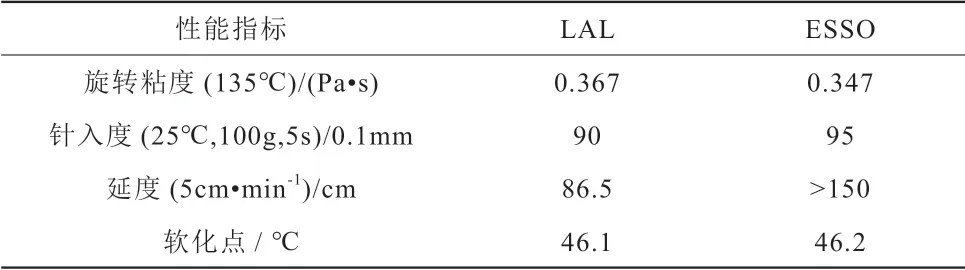
表1 瀝青基本性能指標Table 1 Basic performance indexes of asphalt

1.2 基于HHT算法的流變信號邊際譜表示

依據HHT原理,采用經驗模式分解(Empirical Mode Decomposition, EMD(計算流變時域信號時能夠獲取大量的基本模式分量,采用Hibert變換這些分量,能夠獲取流變信號中與時間、瞬時頻率相關的函數H(w,t),由此,可以通過公式(1)描述邊際譜：

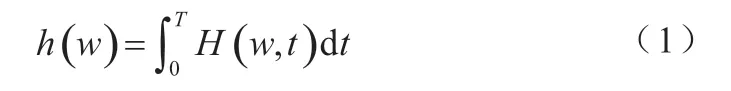
公式(1)中,流變信號的全部采樣時間由T表示；流變信號的Hilbert時頻譜由H(w,t)描述,依據該公式的計算,邊際譜h(w)可以描述為幅值譜針對時間的積分。

在現實中的流變信號提取時,并不一定需要采集到完整流變信號的全局譜,通常采用邊際譜計算EMD分解后信號中的某個IMF,因此,也可以針對每個IMF,進行局部邊際譜計算,并通過公式(2)表示,其中,IMF為本征模態函數(Intrinsic Mode Function,IMF)。

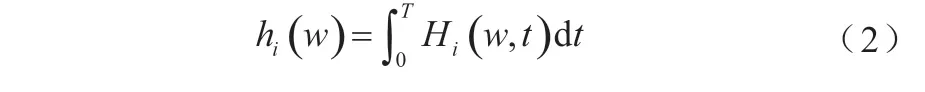
公式(2)中,采用EMD算法分解流變信號后,第i個IMF的局部邊際譜由hi(w)描述。

1.3 基于邊際譜的流變特性特征提取

1.3.1 譜能量特征

在流變信號提取過程中,廣泛采用能量特征的提取,實現流變特性提取。由于邊際譜表示中,頻點在全部流變信號內存在的頻率可通過一個頻率點處幅值大小進行評判[11-12],因此,譜能量實際上為統計形式的能量。依據流變信號能量的分析,通過公式(3)表示邊際譜能量的計算：

公式(3)中,流變信號的邊際譜由h描述；流變信號頻帶寬度由k描述,e為邊際譜能量,f表示包絡點數值。

同時,在提取IMF時可知,分解時能夠提取到單個細節信號與頻率不高于細節信號的低頻分量。因此,采用EMD算法分解流變信號,即為從高頻率到低頻率的提取方式[13-14],當分解完成后,能夠獲取n個基本模式分量,其中頻率最高為c1(t),頻率最低為cn(t),并通過rn(t)表示分解得到的單調序列。

上述分解過程與小波變換分解較為相似,因此可以將某個IMF相應邊際譜能量作為特征值進行計算,并通過公式(4)表示：

公式(4)中,第i個基本模式分量由ci表示；該分量的瞬時頻率寬度由k表示。

1.3.2 譜熵特征

早期學者在熱力學計算中提出熵這一概念,熵是指在空間中,能量排列混亂情況的一種度量[15],當能量排列越混亂,能量的熵值即越高。為此引入Shannon熵概念,通過公式(5)表示其計算過程：

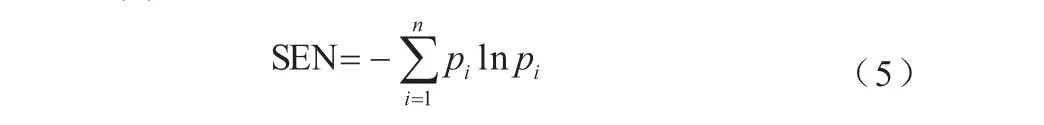
公式(5)中,概率密度由pi表示,其表示事件出現的概率,該事件可能是某組特征向量內的某個特征值。當采用Shannon熵計算時,能夠計算得到數據的全局熵,還能夠計算得到部分數據中的局部熵。

目前實現Shannon熵的計算過程優化主要有兩種計算形式,分別為Renyi熵與Tsallis熵,其中,Renyi熵通過公式(6)表示：

Renyi熵在進行計算時僅在Shannon熵基礎上附加了一個參數α,通過該參數,調整概率分布曲線的敏感度。

Tsallis熵通過公式(7)計算：

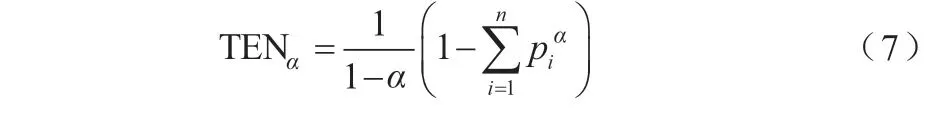
Tsallis熵同時也包含附加的參數α,當參數α接近1時,兩種熵的計算形式均與Shannon熵保持一致。

Tsallis熵形式類似于Shannon熵,也附加一個參數。另外,可以發現當參數α趨近于1的時候,兩者最終演變為Shannon熵。

譜熵是熵的最佳表現形式,其能夠分析出某個時間序列譜的復雜度,通常情況下,譜延伸越寬,即存在越大熵值,若譜延伸情況較差,則熵值越小。在譜變換時,本文采用傅里葉變換法計算譜熵。在熵計算時,需提前通過歸一化調整邊際譜的概率密度值,通過公式（8）表示轉換過程：

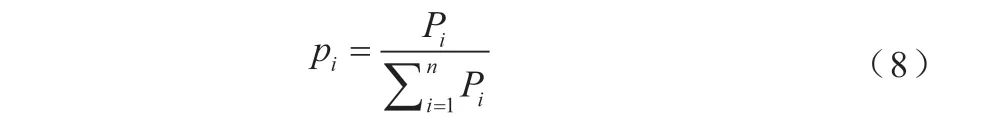
公式(8)中,譜的概率密度值由pi描述；第i個頻率成分的能量由Pi描述。依據所提取的譜能量特征與譜熵特征,即能夠實現流變特性的特征提取。

2 試驗分析

2.1 瀝青老化前后特性分析

對本文選取的兩種基質瀝青進行短期老化試驗,選取82型旋轉薄膜烘箱作為試驗機器,分別對每種瀝青取35±0.5 g試樣放置至老化瓶中,設定烘箱溫度為163±0.5 ℃ ,設定空氣流量為(4000±200)mL/min,同時將烘箱旋轉速度設為(15±0.2)r/min,老化時間選定為360min,進行薄膜烘干,得到短期老化后的試樣。對短期操作后的瀝青殘留物繼續壓力老化分析,模擬瀝青長期老化,選取9300型壓力老化容器,設老化溫度為180℃,空氣壓力2.1MPa,測試時間為24h。

2.1.1 瀝青旋轉黏度分析

通過瀝青溶液的黏度能夠反映出相對分子量。對相同物質而言,黏度越高即該物質具有越大分子量。當瀝青老化時,必然包含化學鍵的變化與聚合,因此會導致黏度一并發生變化,因此,通過黏度變化的分析,得出瀝青老化前后的流變狀態,通過表2分析不同瀝青老化狀態的旋轉黏度。

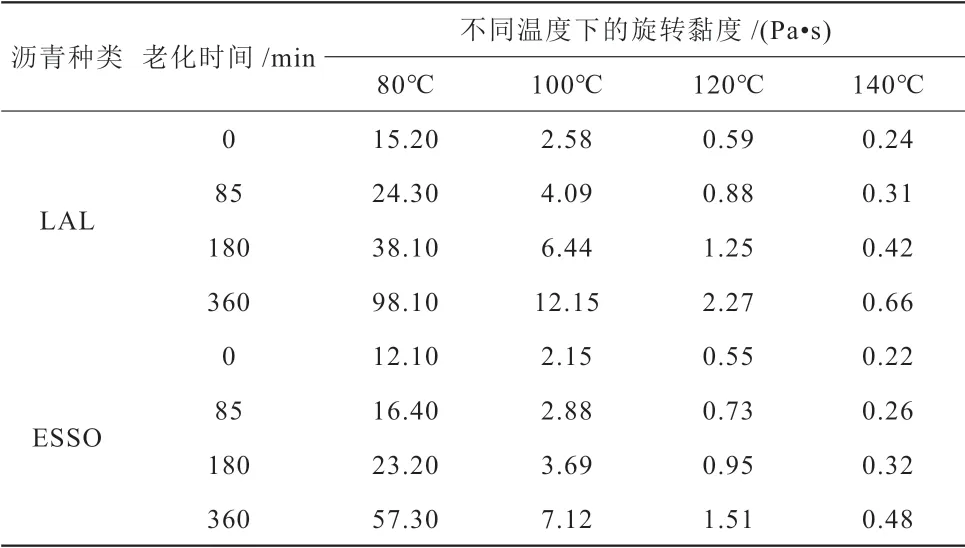
表2 不同瀝青老化旋轉黏度Table 2 Aging rotational viscosity of different asphalt

表2中,兩種瀝青隨著老化時間增加,旋轉粘度逐漸增加,即老化時間越長,瀝青流變特性越差,但當一種瀝青處于同一老化時間時,溫度較高會使黏度降低,說明當溫度過高時,兩種瀝青的黏度均會變差。當溫度處于80℃時,瀝青的旋轉黏度最高,流變特性最差。

2.1.2 瀝青軟化分析

以延展度和軟化點溫度為衡量瀝青軟化度指標,分析兩種瀝青軟化情況,結果如圖1所示。

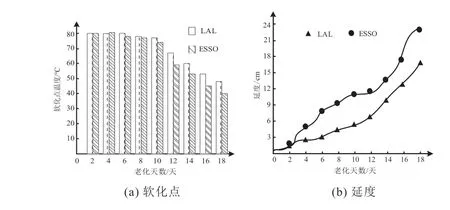
圖1 兩種瀝青軟化情況Fig. 1 Softening of two kinds of asphalt

由圖1(a)可知,隨著老化天數的增加,兩種瀝青的軟化點溫度逐漸降低。其中在老化天數為4天之前,LAL和ESSO瀝青的軟化點溫度相同,均為80℃；在老化的第6天時,LAL軟化點溫度保持80℃；而ESSO瀝青的軟化點溫度開始呈現下降趨勢；隨著老化天數的增加,LAL瀝青軟化點溫度始終高于ESSO瀝青,在老化的第18天時,LAL瀝青軟化點溫度較ESSO瀝青軟化點溫度高約9℃,該結果表明LAL瀝青耐高溫性能優于ESSO瀝青。

由圖1(b)可知,兩種瀝青的延度與老化天數成正比例關系。在老化的前2天時,兩種瀝青的延度曲線幾乎重合,其初始延度約為1.5cm,隨著老化天數的增加,ESSO瀝青延度曲線呈波浪狀上升趨勢,當老化天數為18天時,其延度數值達到23.8cm左右；而LAL瀝青延度曲線呈現較為平緩上升趨勢,上升幅度低于ESSO瀝青,當老化天數為18天時,其延度數值為17cm左右,較ESSO瀝青延度數值低6.8cm。綜合圖1結果可知,LAL瀝青耐高溫能力和變形能力均較ESSO瀝青好。

2.1.3 穩定性分析

從穩定性角度對兩種瀝青展開分析,以穩定度損失率作為衡量瀝青老化過程中穩定性指標,分析不同老化時間時,兩種瀝青穩定情況,結果如圖2所示。

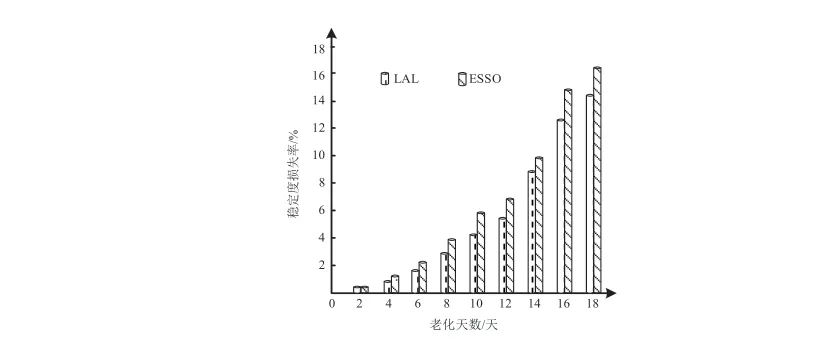
圖2 兩種瀝青穩定性測試結果Fig. 2 Stability test of two kinds of asphalt

分析圖2可知,兩種瀝青的穩定度損失率隨著老化天數的增加而增加。在老化天數為2天時,兩種瀝青的穩定度損失率相同,數值約為0.6%左右；隨著老化天數的增加,ESSO瀝青的穩定度損失率數值增長速度始終高于LAL瀝青,當老化天數為18天時,ESSO瀝青的穩定度損失率較LAL瀝青高2.5%左右,該結果表明,LAL瀝青穩定性較ESSO瀝青好。

為更好地分析兩種瀝青穩定性,以流值作為衡量其老化穩定性附加指標,流值即為瀝青流動數值,其單位為mm,分析不同老化天數時,兩種瀝青的流值變化情況,結果如圖3所示。

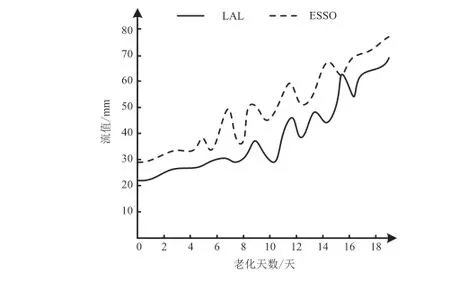
圖3 兩種瀝青流值變化情況Fig. 3 Change of two kinds of asphalt flow value

分析圖3可知,瀝青流值與老化天數成正比例關系。在老化天數為4天之前,兩種瀝青的流值初始數值雖然不同,但其流值曲線呈現平緩上升趨勢；當老化天數為4～17 天左右時,兩種瀝青的流值曲線呈波浪狀上升趨勢；當老化天數超過17天后,兩種瀝青流值曲線又恢復平穩上升趨勢,其原因在于兩種瀝青在老化之初瀝青結構穩定性較好,隨著老化溫度的增加,瀝青結構被破壞,使其流動性增強,當瀝青老化到一定程度后,瀝青結構又呈現相對穩定趨勢,因此在老化天數超過17天之后,兩種瀝青的流值曲線呈現平穩上升趨勢。從流值數值方面分析,LAL流值曲線始終低于ESSO瀝青,表明其穩定性較好。

2.2 流變特性提取分析

2.2.1 流變信號的邊際譜表示

通常情況下,瀝青老化前后流變信號是一種典型的非平穩信號,通過邊際譜的形式,能夠有效展現流變過程的非平穩信號,在瀝青老化過程中,流變信號會在頻率軸上出現明顯能量分布差異,對LAL瀝青進行特征提取,通過圖4表示瀝青老化前后的流變特性。

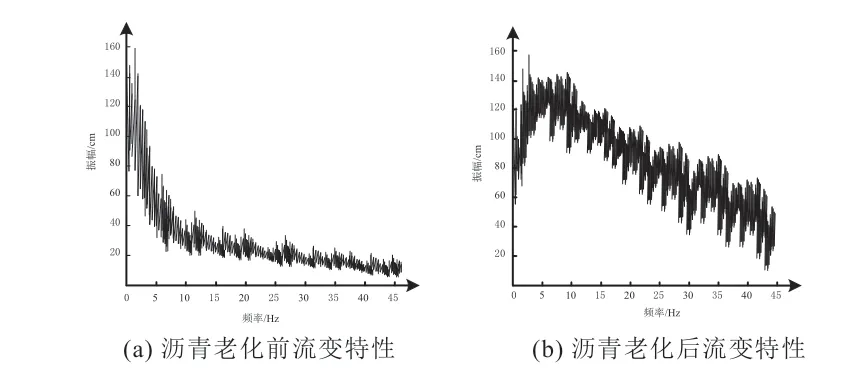
圖4 瀝青老化前后流變特性提取Fig. 4 Extraction of rheological properties of asphalt before and after aging

根據圖4可知,老化前的瀝青流變特性波段能量要小于老化后的瀝青流變特性波段能量,因此,采用本文方法能夠精確實現瀝青老化后的流變特性提取。

2.2.2 瀝青老化前后流變信號譜熵特征提取

瀝青老化前后流變信號的邊際譜熵特征存在顯著性差異性,為此通過檢測瀝青老化前后流變信號的Shannon熵、Tsallis熵和Renyi熵三種邊際譜熵特征價值度的差異性,驗證本文方法的流變特性提取能力,瀝青老化前后流變信號的邊際譜熵特征價值度情況如圖5所示。

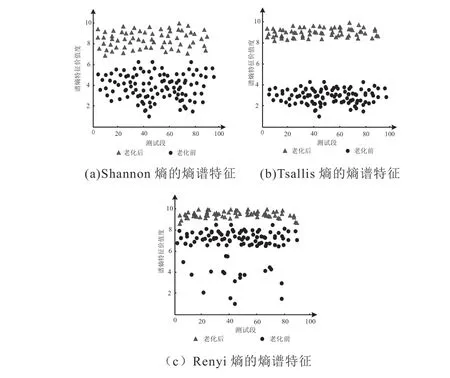
圖5 老化前后流變譜熵特征價值度分析Fig. 5 Value analysis of entropy characteristics of rheological spectrum before and after aging

根據圖5可知,在不同被測段中,老化后瀝青流變信號的三種邊際譜熵特征價值度分布要明顯高于老化前,三種邊際譜熵特征提取方法均能夠較好地提取熵譜特征價值度。因此,通過本文方法提取的流變特征能夠實現較為精準區分瀝青老化前后狀態,衡量瀝青老化情況。

3 結論

本文通過HHT算法,提取瀝青老化前后流變譜熵特征,并通過試驗分析兩種瀝青老化前后的流變情況,并驗證本文方法瀝青老化前后流變特性提取的有效性,可通過所提取特征準確衡量瀝青老化情況。在未來階段可對該提取方法進一步研究,實現更加全面的瀝青變化特征提取。