混凝土容重和施工工藝對連續梁橋位移敏感性的影響

劉經偉

（云南省交通規劃設計研究院有限公司，云南 昆明 650011）

0 引言

改革開放以來尤其是2010年以來，連續梁橋和連續剛構橋由于跨徑大、結構良好的特點在高速公路、鐵路中得到了較為廣泛地應用，尤其是在西北、西南山區。自然環境、氣候的長期作用，重車、超重超限車輛持續增加和人為事故的影響，相當數量的連續梁橋出現了不同程度的病害，對于連續梁橋的運營安全、耐久性和服役能力造成了較大的影響。為了成橋后橋梁結構的線形、合龍精度和結構內力滿足設計要求，同時保證懸臂施工的安全，需要對連續梁橋的懸臂施工過程進行施工監控。施工監控是隨著大跨徑橋梁的發展而逐步發展推廣起來的，已經成為當前橋梁尤其是連續梁橋建設中不可或缺的一部分。鑒于影響連續梁橋施工過程和成橋后線形和受力狀況的系統參數較多，本文主要介紹連續梁橋系統參數的位移敏感性，并結合實例分析混凝土容重和施工工藝對于連續梁橋的位移敏感性的影響，研究結果對于未來類似橋梁的施工監控和后期維護提供了一定的理論和工程經驗。

1 連續梁橋的施工監控

結合設計圖紙和現場實際情況對橋梁進行建模計算分析，確定橋梁結構在分塊澆筑過程以及成橋后的線形和受力情況，保障計算滿足規范和設計要求。鑒于連續梁橋的施工過程較為復雜，施工中如澆筑塊自重、結構強度、剛度、預應力和相對濕度以及外界環境因素對于連續梁橋的變形和內力有較大的影響，施工過程中需要給予重視，避免橋梁施工過程中或者成橋后受力情況和結構變形與理論計算差別太大，從而導致成橋后的線形和受力狀況不滿足設計要求和服役要求。對于施工監控過程，需要在施工的每一個過程，通過理論計算得到結構內力和線形，同時通過現場測量得到實際值。如果現場實測數據與理論計算值差別較大，應及時查找原因，在未處理之前不得進一步施工作業，保證橋梁結構在施工過程和成橋后的線形和受力情況處于安全范圍之內。

2 敏感性分析

對于連續梁橋的線形和受力狀況，不同參數的影響程度，尤其是同一個參數對于不同的橋梁結構的影響程度也是不同的，因此對于連續梁橋的系統參數需要進行敏感性分析，即狀態參數發生一定程度的變化后，研究對應的結構關鍵控制截面的位移（內力）的變化幅度。對于系統參數敏感性分析，需要根據結構狀態影響的系統參數的不同，將影響參數分為主要狀態參數和次要狀態參數，即主要狀態參數對于結構的影響較為顯著，而次要狀態參數的影響相對較弱，從而對施工監控過程和成橋后線形控制進行參數的針對性處理，確保結構在施工過程中和成橋后均能滿足服役要求和相關規范。

2.1 分析步驟

本文主要介紹連續梁橋系統參數的位移敏感性。關于位移敏感性的分析步驟如下：

（1）調整系統參數，控制變化幅度在5%以內；

（2）確定關鍵截面和控制目標，建立不同參數與控制目標的關系式；

（3）根據系統參數對關鍵截面和控制目標的影響程度不同，區分主要狀態目標和次要狀態目標；

（4）根據以上步驟，列出以下具體過程：

取任一狀態參數x，控制目標位y，可得關鍵截面的撓度或者應力等，則y=f( )x，給予x一個微變量Δx（參數基準值5%以內），可以得到以下關系式：

上式中，x0為參數基準值。

對于系統參數敏感性分析的目標值，則可以選擇下式表示：

從（3）式可知，β值越大，參數對于控制目標的影響越大，即控制目標對于該參數變化越敏感。

2.2 控制指標

選擇橋梁線形作為主要控制目標，進行混凝土容重和施工控制參數的位移敏感性分析。選擇單梁在最大懸臂狀態下的累計撓度差值的絕對值相加，取絕對值之和作為控制目標β1，具體如下式所示：

式中：

n——單梁段數；

d——累計撓度，其中di0為參數取基準值時的撓度，di1為參數調整一定程度后的累計撓度。

對于關鍵截面的控制目標值，當前主要存在撓度和應力兩種情況，由于其性質、大小和單位均有一定程度的差別，因此對于參數的敏感性進行分析時，需要對于關鍵截面的控制目標值進行歸一化處理，關鍵表達式如下式所示：

對于歸一化取值，本文選擇取值不小于0.3的參數為主要狀態參數。

3 工程背景

3.1 工程概況

某橋梁上部結構采用116m+220m+116m 三跨連續剛構結構，雙幅布置；墩身采用雙肢等截面布置，樁基采用鉆孔灌注樁基礎，D=2.50m，總體布置如圖1所示。

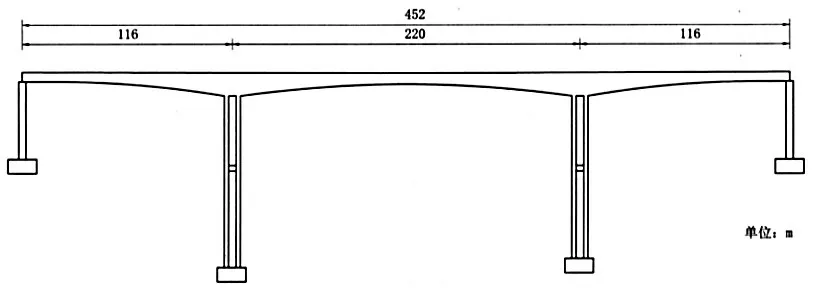
圖1 某橋梁總體布置（單位：m）

3.2 有限元模型

采用MIDAS Civil有限元軟件建立橋梁結構模型，按照連續剛構橋懸臂澆筑施工順序進行分段處理，橋墩和主梁均采用梁單元處理，墩身固結處理，計算時考慮時間依存效應[1-5]。模型澆筑段劃分如圖2所示。

圖2 某橋梁施工節段劃分（單位：m）

根據圖2可知，0#段長度為18.0m，橋墩施工完畢后，托架澆筑施工，每個懸臂現澆“T”梁順橋向分為28節段，懸臂節段最大重量2750kN，掛籃自重為1200kN。合龍順序為先邊跨后中跨。

關于一期恒載，按照橋梁實際構件進行計算；二期恒載選擇為65kN∕m。公路-Ⅰ級荷載，計算考慮偏向荷載、沖擊和車道折減系數的影響。

4 混凝土容重/施工控制參數敏感性分析

4.1 參數選取

結合連續梁橋的特點，混凝土彈性模量E、混凝土容重ρ、張拉齡期t、張拉控制應力σcon、管道摩阻系數μ、管道偏差系數k、預應力鋼筋松弛率ξ、錨具回縮量ΔL、環境相對溫度RH、徐變系數修正系數Cx、收縮系數修正系數Cs、混凝土熱膨脹系數α和施工過程均會對橋梁結構的線形和受力情況造成影響，本文就混凝土容重和施工過程的位移敏感性進行分析。

4.2 容重均勻變化

對于連續剛構橋的自重誤差，當前主要來源于混凝土容重、梁段成型誤差[6-7]。對于當前混凝土設計采用的高等級混凝土而言，鑒于其密實度較高，多數混凝土的容重相比規范值大，對于某橋梁混凝土容重設計值γ=27.3kN∕m3，混凝土容重分別選擇0.9γ、1.0γ和1.1γ時，單T主梁在最大懸臂狀態下的應力值如表1所示。

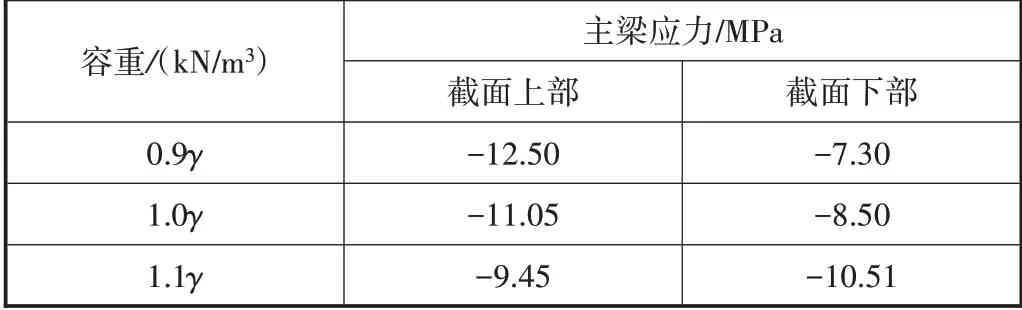
表1 懸臂施工混凝土不同容重時主梁應力

從表1可知，在容重變化量為10%時，主梁控制截面下部的應力發生變化，幅度在1.5MPa左右。在容重發生變化時，主梁控制截面撓度變化對比如圖3所示。

圖3 容重取不同值時的主梁撓度

從圖3可知，在容重變化幅度為10%時，主梁控制截面的撓度最大變化量為20mm。

在實際施工過程中，混凝土容重在施工中與設計規范往往有較大偏差。容重的增加會使得梁體控制截面撓度增大，同時施工過程中的模板剛度不足或者結構尺寸誤差都會使主梁撓度增大，因此在施工過程中需要嚴格控制施工工藝，避免容重增加造成主梁撓度偏差超過規范誤差范圍。

4.3 T構兩側主梁自重不平衡

由于連續剛構橋以橋墩為對稱中心，單T兩側梁段進行懸臂澆筑，由于容重或者尺寸不一致，會導致T梁梁段質量不對稱，本文以主梁一側取混凝土容重1.05γ、1.1γ，另一側混凝土容重選擇1.0γ，計算可以得到最大懸臂下的主梁控制截面撓度和應力，如圖4和表2所示。

表2 T構兩側容重不平衡時主梁關鍵截面內力

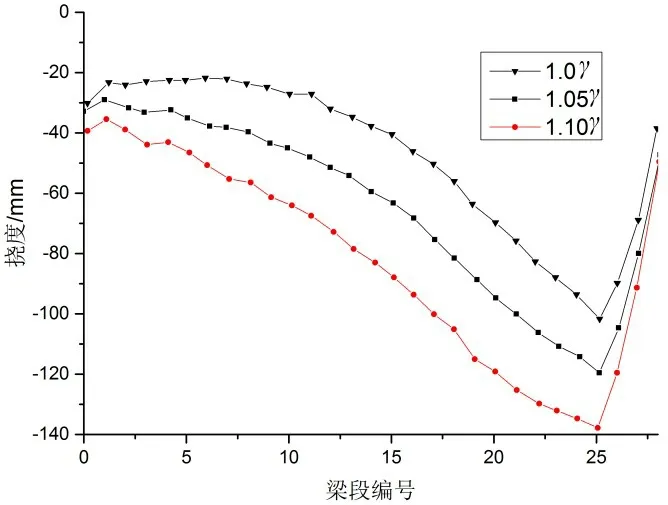
圖4 T端對稱不平衡時超重側主梁撓度

從圖4和表2可知，單側混凝土的容重增加10%，主梁控制截面、墩頂和墩底截面應力變化最大值為1.5MPa，撓度的最大變化值為50mm。

4.4 施工進度不一致時的應力和撓度

鑒于連續剛構橋懸臂施工過程中存在較大的不可控性，因此T構對稱兩面施工進度不一致是不可避免的，因此本工程考慮澆筑超前5.0m3、10.0m3，計算得到主梁在最大懸臂狀態下的應力和撓度如表3所示。

從表3可知，當T構單梁單側混凝土澆筑超前10.0m3時，主梁應力增加幅度為0.2MPa左右，主梁懸臂端撓度變化幅度在16.0mm。

5 結束語

在連續剛構橋懸臂施工過程中，參數敏感性分析和控制指標是工程質量控制的關鍵因素，以實際工程為例，對位移和應力敏感性進行分析，主要得到以下結論：

（1）在容重變化幅度為10%時，主梁控制截面的撓度最大變化量為20mm；

（2）當T構單梁單側混凝土澆筑超前10.0m3時，主梁應力增加幅度為0.2MPa左右，主梁懸臂端撓度變化幅度在16.0mm。