我是小小建筑師

潘俊儀

一、教學(xué)內(nèi)容

人教版《義務(wù)教育教科書·數(shù)學(xué)》五年級下冊第70頁。

二、教材簡析

小學(xué)五年級數(shù)學(xué)下冊最小公倍數(shù)在生活中的應(yīng)用（例3），和前面公因數(shù)的實際應(yīng)用編排一致，教材延續(xù)前面的素材，創(chuàng)設(shè)了用長方形墻磚鋪正方形的實際問題情境，用公倍數(shù)、最小公倍數(shù)的知識求正方形的邊長及其最小值。

教材同樣呈現(xiàn)解決問題的全過程。首先通過畫圖初步理解題意，感受鋪出正方形的不確定性。然后，找出解決問題的方法。也就是將實際問題轉(zhuǎn)化為數(shù)學(xué)問題，即“正方形的邊長必須既是3的倍數(shù)又是2的倍數(shù)”。這樣就可以利用公倍數(shù)和最小公倍數(shù)來解決了。最后，利用畫圖驗證的策略來檢驗，并結(jié)合前面學(xué)習(xí)的經(jīng)驗，總結(jié)出解決這類問題的關(guān)鍵就是將實際問題轉(zhuǎn)化為數(shù)學(xué)問題。

三、教學(xué)對象

學(xué)生掌握了兩個數(shù)的最小公倍數(shù)的方法，在經(jīng)歷應(yīng)用最大公約數(shù)解決實際問題的過程中，發(fā)展了將實際問題轉(zhuǎn)化為數(shù)學(xué)問題的意識。但是將實際問題轉(zhuǎn)化為數(shù)學(xué)問題的能力仍需在不同情景中，通過轉(zhuǎn)化、操作、觀察、分析、解決、反思，逐步強化轉(zhuǎn)化能力和應(yīng)用能力。部分學(xué)生能需要借助直觀圖幫助理解問題中的數(shù)量關(guān)系;部分學(xué)生能根據(jù)用最大公因數(shù)解決問題的經(jīng)驗，找到解決本節(jié)實際問題方法。動態(tài)的圖例，讓抽象的邏輯在直觀中明晰;豐富的交流活動，讓各種方法在思辨中深化;形式豐富的練習(xí)，讓轉(zhuǎn)化能力在層層練習(xí)中強化。

四、教學(xué)目標(biāo)

1.能將實際問題轉(zhuǎn)化為“求最小公倍數(shù)”的數(shù)學(xué)問題，運用數(shù)形結(jié)合的方法理解題意，應(yīng)用最小公倍數(shù)知識解決問題。

2.通過探索、操作、交流等活動，在具體情境中強化分析、轉(zhuǎn)化、應(yīng)用能力和優(yōu)化意識。

3.在豐富的學(xué)習(xí)活動中，體味數(shù)學(xué)源于生活，應(yīng)用于生活。

五、教學(xué)重、難點

1.重點：用公倍數(shù)和和最小公倍數(shù)的知識解決簡單的實際問題。

2.難點：將實際問題轉(zhuǎn)化為數(shù)學(xué)問題。

六、教學(xué)準(zhǔn)備：研學(xué)案、課件

七、教學(xué)過程

（一）課前游戲

教師組織學(xué)生進(jìn)行熱身游戲，利用學(xué)生的學(xué)號進(jìn)行公倍數(shù)知識的鞏固。

師：當(dāng)老師說出兩個數(shù)，如果你的學(xué)號是這兩個數(shù)的公倍數(shù)，請迅速站起來，并響亮說出你的學(xué)號。

設(shè)計意圖：為了調(diào)節(jié)課堂氣氛、激發(fā)學(xué)生思考的積極性，設(shè)計了形式特別且有趣的游戲。調(diào)動學(xué)生思維和反應(yīng)，鞏固最小公倍數(shù)的知識，起到“溫故而知新”的作用。

（二）課中互動

1.研學(xué)探究

融入情境。微課展示小小建筑師解決問題情境。

設(shè)計意圖：有趣的微課讓學(xué)生融入情境，微課中的角色對話逐步點燃學(xué)生探索的積極性。盲目的鋪磚過程讓學(xué)生直觀感受到其中的不便利，引導(dǎo)學(xué)生著手思考將生活問題轉(zhuǎn)化為數(shù)學(xué)問題。

2.閱讀與理解

（1）教師引導(dǎo)學(xué)生明確解決問題的三個步驟

師：現(xiàn)在小儒和小雅遇到這樣一個問題，我們既然要參與解決，就要先明晰解決問題的步驟。

生：閱讀與理解、分析與解答、回顧與反思。

（2）學(xué)生收集信息，理解問題

師：我們要解決什么問題？

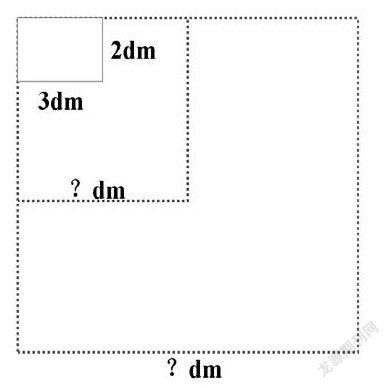
生：用墻磚鋪一個正方形，求這個正方形的邊長可以是多少分米，最小是多少分米。（板書）

師：要解決這個問題，還需要知道什么信息？

生：磚墻的長是3分米，寬是2分米。（板書）

師：在鋪的過程中，有什么要求？

生：用的墻磚必須都是整塊，不能切開。

師：明明是鋪磚問題，現(xiàn)在我們轉(zhuǎn)化為數(shù)學(xué)問題。

3.分析與解答

（1）分析問題

①合作初探

師：請你根據(jù)合作要求進(jìn)行小組合作，拼一拼、說一說。

合作要求：

拼：用小紙片（長3厘米，寬2厘米的長方形）代替墻磚拼正方形。

思考：能拼成邊長是多少厘米的正方形？你能拼成邊長是8厘米的正方形嗎？你們發(fā)現(xiàn)了什么？

②匯報分析

學(xué)生上臺匯報展示。

預(yù)設(shè)：我們鋪成邊長是6厘米的正方形，不能鋪成8厘米的正方形。我們發(fā)現(xiàn)6是2的倍數(shù)和3的倍數(shù)，也就是2和3的公倍數(shù)。

師：那么要求正方形邊長是多少分米，還需要繼續(xù)拼嗎？

分析：用的墻磚都是整塊的，因此，正方形的邊長既是2的倍數(shù)，又是3的倍數(shù)。因此，只要找出2和3的公倍數(shù)，就能知道正方形的邊長可能是多少分米。

（2）解答問題

學(xué)生獨立寫出應(yīng)用最小公倍數(shù)知識解決問題的過程，學(xué)生展示匯報，教師點撥。

設(shè)計意圖：學(xué)生對于倍數(shù)關(guān)系的感知需要借助直觀手段，因此，設(shè)置了擺一擺的過程，讓學(xué)生親身體驗拼正方形的過程。通過試拼邊長是6厘米的正方形和8厘米的正方形，激發(fā)學(xué)生深入思考正方形邊長與長方形長和寬的關(guān)系，從而悟出正方形邊長是2和3的公倍數(shù)，突破本節(jié)重難點。

4.優(yōu)化方法，回顧與反思

教師引導(dǎo)學(xué)生應(yīng)用畫圖等方式進(jìn)行回顧反思，學(xué)生通過觀看微課，領(lǐng)悟如何更快捷鋪正方形。

師：解決問題的方法真多樣。嚴(yán)謹(jǐn)?shù)慕ㄖ煏Y(jié)果反復(fù)檢驗，要是你，你將怎么檢查？

生：再算一遍。

生：用了短除法的話，就用篩選法檢驗。

師：嗯，除了用算的方式檢驗，還可以用畫圖或者擺拼來檢驗。

師：解決完這個問題，小儒和小雅有了新發(fā)現(xiàn)。

學(xué)生觀看微課。

師：在實際生活中，為了更具特色，不僅可以整齊地鋪磚，還可以相互交錯地鋪磚。（PPT展示）

設(shè)計意圖：數(shù)學(xué)應(yīng)用于生活才能體現(xiàn)它最大的價值。因此，將求所得的結(jié)果，應(yīng)用在提高鋪磚效率上。原來無序地試探性鋪磚，耗費大量時間;現(xiàn)在已經(jīng)求出了正方形的邊長，可以先鋪好第一行和第一列，再填充剩余部分，提高鋪磚效率。在第二次鋪磚過程中，滲透優(yōu)化的數(shù)學(xué)思想和應(yīng)用數(shù)學(xué)的意識。

（三）研學(xué)練習(xí)

學(xué)生獨立解決問題，交流匯報，深化理解應(yīng)用最小公倍數(shù)和最大公因數(shù)解決問題的本質(zhì)。

師：接下來，帶上你的本領(lǐng)來工程隊，試試解決遇到的下面兩個情況吧。

師：學(xué)生小組交流一下，這個問題應(yīng)用了什么知識來解決？為什么？

師：為什么兩個問題應(yīng)用不同的知識來解決？

師：因此，我們遇到類似情況的時候，要怎么分析？或者說要關(guān)注什么？

設(shè)計意圖：結(jié)合了本節(jié)課主題，設(shè)計了貼合主題的兩個情境，強化了轉(zhuǎn)化為數(shù)學(xué)問題的能力。其中，情境一和情景二分別應(yīng)用了最小公倍數(shù)和最大公因數(shù)解決問題，學(xué)生容易因缺乏認(rèn)知思考，錯用最小公倍數(shù)解決情景二的問題。這時，“我會填”的分析過程引導(dǎo)學(xué)生理清思路，明辨兩情境中的異同，抓住兩問題的本質(zhì)，強化應(yīng)用最大公因數(shù)和最小公倍數(shù)的能力。

（四）總結(jié)分享

師：回顧一下我們今天當(dāng)“小小建筑師”的點點滴滴，并談?wù)勀憬裉祗w驗中的收獲吧。

設(shè)計意圖：在回顧中強化解決問題的步驟，并引導(dǎo)學(xué)生自主進(jìn)行總結(jié)，將收獲提升到數(shù)學(xué)思想方法、技能層面，讓學(xué)生明白：幫助我們解決生活問題的不僅是數(shù)學(xué)知識，更是數(shù)學(xué)的技能和思想方法。

（五）研學(xué)拓展

師：學(xué)無止境，虛心地學(xué)學(xué)我國古人的智慧吧。

淮安民間傳說有一則故事——“韓信點兵”。韓信帶1500名士兵打仗，戰(zhàn)死四五百人。剩下的士兵站3人一排，多出2人;站5人一排，多出4人;站7人一排，多出6人。韓信馬上說出人數(shù)：我軍士兵有1049人。

師：韓信是怎么知道的呢？

小組交流，分享解題的想法。

設(shè)計意圖：課外數(shù)學(xué)知識既是學(xué)生的興趣所在，更是學(xué)生數(shù)學(xué)素養(yǎng)的發(fā)展需求。結(jié)合中國古代著名的“韓信點兵”故事，讓學(xué)生通過合作研討，跳出思維定勢，鍛煉數(shù)學(xué)思維的靈活性。

八、板書設(shè)計

我是小小建筑師

用最小公倍數(shù)解決簡單問題

（一）閱讀與理解

正方形的邊長可以是多少分米？最小是多少分米？

（二）分析與解答

2和3的公倍數(shù)有6、12、18、24…

（三）回顧與反思

答：正方形的邊長可以是6dm、12 dm、18 dm，…，最小是6dm.

[本文系廣州市番禺區(qū)“十四五”第一批教育科學(xué)規(guī)劃課題“基于融·樂課堂理念下小學(xué)數(shù)學(xué)中高年段‘?dāng)?shù)與代數(shù)’思維培養(yǎng)的策略及應(yīng)用研究”（課題批準(zhǔn)號：2021-PY549）研究成果]

責(zé)任編輯? 陳紅兵