基于BP 神經網絡算法的短期電力負荷預測研究

蘇 顏，張 珍，林慶達，侯 劍，吳 燕

（廣西電網有限責任公司南寧供電局系統運行部，廣西南寧 530023）

由于電能不能大量儲存，必須即發即用，在電力的生產和使用過程中必須保證電力供需平衡，因此，對電力負荷的精準預測是實現電能有效調度的必要前提。通過對歷史負荷數據分析，制定短期電力負荷預測工作[1-4]。電力負荷預測興起于20 世紀80 年代，受制于當時的技術條件，相關的預測方法是由經驗得出的，但這種方法得到的預測值誤差較大。隨著科學技術的發展，電力調度機構對負荷預測的精度有了更高的要求[5-6]。

國外學者利用趨勢外推法進行電力負荷預測，包括水平、線性、多項式等季節性預測方法。但在實際應用中，該方法的預測精度極低，所以并不常用于工程實踐[7]。國內學者提出了灰色模型預測方法，將雜亂無章的數據進一步建模，生成有規律的數列，得到預期目標值[8-9]。而灰色模型預測方法需要大量的數據支撐，且需要建立微分方程進行建模[10]。專家系統法也用于負荷預測，但該方法的缺陷是不一定均能轉化為應用程序[11]。

針對以上方法的不足，該文應用BP 神經網絡法對電力負荷進行短期預測，該方法能夠有效提高負荷預測的準確性。

1 BP神經網絡建模

1.1 BP神經網絡模型

與其他方法類似，BP 神經網絡進行短期電力負荷預測時需得出準確的表達式，才能得到更為精確的預測結果。BP 神經網絡的核心思想是誤差反向傳播，其原理為實際值與誤差值之差的反向傳播過程。通過不斷修正誤差閾值，得到正常范圍內的實際值[12-14]。

神經網絡以人腦為基礎，各個神經元接收神經末梢的感知信息，且多個神經元組成神經網絡，并建立神經網絡模型，其神經元結構如圖1 所示。

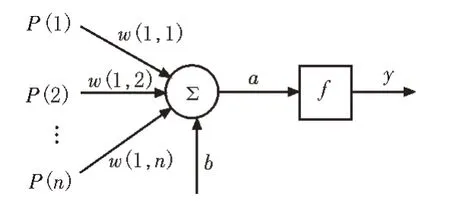
圖1 神經元結構

圖中P為神經元輸入，w為各個神經元之間的連接權值，b為閾值，f為激勵函數，y為輸出值，可用下式進行表示：

完整的BP 神經網絡通常由三部分組成，即輸入層、隱含層和輸出層。其中，隱含層可包含多層，而輸入層與輸出層一般只有一層，圖2 為多層的BP 神經網絡結構[15-16]。在實際的電力負荷短期預測中，隱含層的層數由實際需求確定。

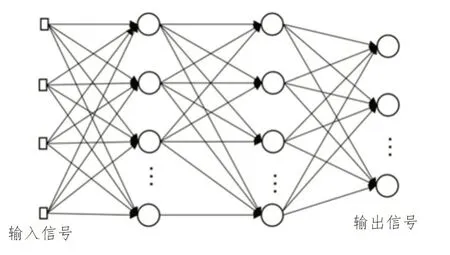
圖2 BP神經網絡結構

1.2 BP神經網絡學習算法

標準BP 神經網絡學習算法通常包含前向傳播和反向傳遞。在前向傳播過程中，隱含層第i節點的輸入Ni為：

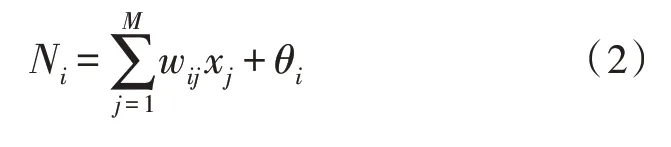
則該節點i的輸出Oi可表示為：

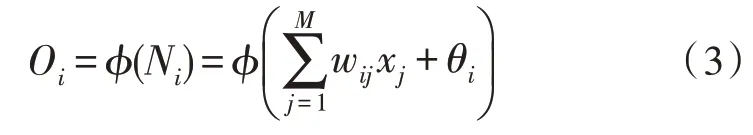
輸出層第k個節點的輸入Nk為：

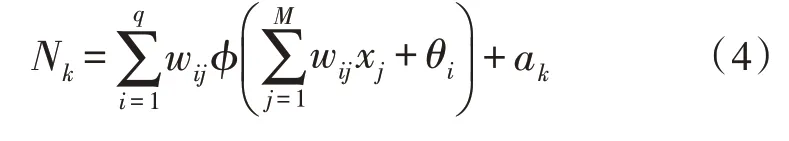
則該節點的輸出Ok為：

式中，ψ為激勵函數。

反向傳播過程是根據計算得出的輸出與實際值之間的誤差對權值和閾值進行調整，從而達到規定的要求。假設誤差函數E為：

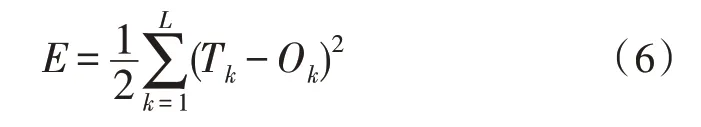
P個樣本的總誤差函數為：

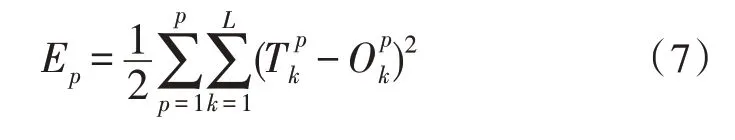
沿誤差函數偏導負方向進行修正，得到的權值修正公式為：

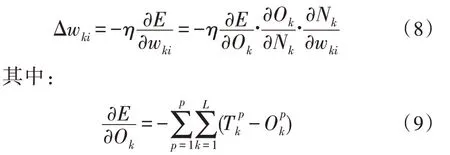
式中，wki為輸入層第i個節點到輸出層第k個節點之間的權值；Ok為輸出層第k節點的輸出結果。

綜上所述，算法的總體流程如圖3 所示。

圖3 BP神經網絡算法流程

2 短期電力負荷預測

2.1 負荷預測的基本步驟

在進行電力負荷預測工作之前，需要確定負荷的預測步驟，目前常用的步驟如下：

1）首先確定負荷預測的時間尺度。時間尺度即長期、短期、超短期和預測的地點并考慮氣候因素，文中的負荷預測為短期電力負荷預測。

2）收集歷史負荷數據。電力數據通常可以通過電力管理部門獲取，天氣數據可以通過氣象部門獲取。

3）對歷史數據進行預處理。針對收集到的數據，檢查數據的合理性和完整性，保證所有數據的準確性并針對性地進行處理。

4）建立預測模型。選取某種方法對區域內的電力負荷進行預測，實際過程中還會通過選取多種方法進行對比分析。

5）誤差分析。通過與實際值進行對比，得到預測誤差值，然后改進算法，從而提高預測的準確性。

2.2 歷史數據預處理

首先建立負荷預測模型，第一步需要收集預測區域的溫度和氣象等信息，確定需要訓練的樣本，并對上述數據進行歸一化處理。

由于歷史數據預處理是短期電力負荷預測的基礎，若歷史數據選取不恰當，則會造成預測結果不準確甚至無法預測的后果；而一個精確的預測結果需要大量的歷史數據進行支撐，因此在進行BP 神經網絡建模前，需要根據具體情況選取合理的歷史數據。

在電力調度部門和氣象部門選取數據是較為可行的渠道，但通過該種方法得到的數據信息仍存在問題。在測量過程中通常存在數據誤差，導致選取的數據有遺漏或誤差極大等因素。因此在進行數據訓練前，需要對獲得的數據進行預處理，以將遺漏的數據補充完整，并對異點進行修正。

異點是指由于各種原因導致數據與真實值偏差過大而出現的數據點，若不經過處理，則會導致總體誤差進一步增大。通常采用水平處理和垂直處理的方法對其進行處置。

1）水平處理方法。通常情況下，負荷曲線是平滑連續變化的，即在兩個相鄰時刻前后的負荷相差不會過大，若相差較大則可能是由于設備出現故障或者人為因素導致。水平處理的原理如下：

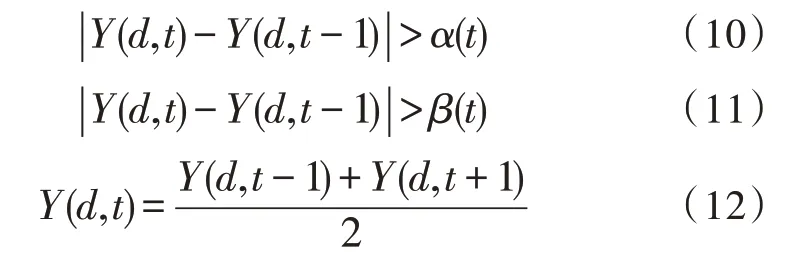
式中，α(t)、β(t)為閾值，Y(d,t+1)表示第d天第t+1 時刻的電力負荷功率，Y(d,t-1)表示第d天第t-1時刻的電力負荷功率，Y(d,t)表示第d天第t時刻的電力負荷功率。

2）垂直處理方法。該方法是針對相鄰日同一時刻的負荷數據來說的，以保證兩者的差距維持在一定范圍內。若超出預設的范圍值，則作以下修正：

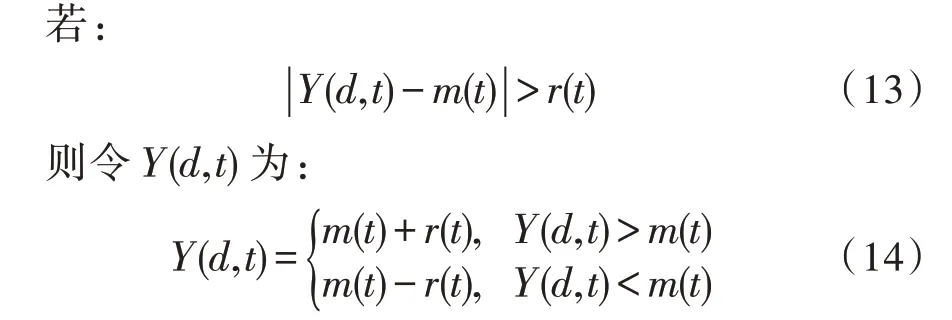
式中，m(t) 表示相鄰天的負荷功率值，r(t) 為閾值。

2.3 樣本數據歸一化處理

BP 神經網絡的激勵函數通常選取為S 型函數，以保證網絡的收斂速度，但會產生誤差。若樣本數據直接使用，則容易導致S 型函數出現飽和現象。因此，需要對數據進行歸一化處理。

數據歸一化處理與激勵函數直接相關，S 型函數通常將負荷數據歸一化至0～1 之間。該文采用的負荷數據歸一化公式為：

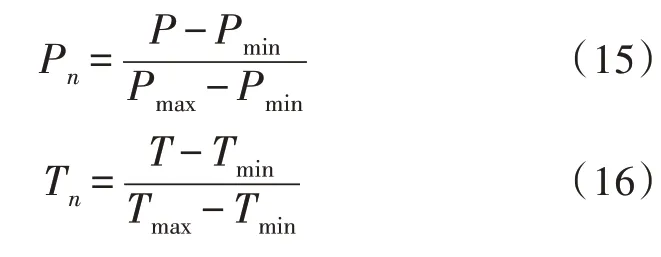
式（15）、式（16）分別為進行過歸一化處理后的數據矩陣和目標矩陣。式中，Pmax、Tmax、Pmin、Tmin分別為歷史輸入數據和目標樣本數據的最大及最小值。其反歸一化公式為：

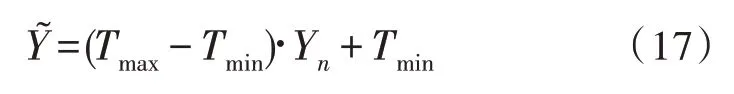
2.4 網絡的拓撲結構

BP 神經網絡的隱含層可以是一層或多層，而輸入層和輸出層只有一層。在建立短期電力負荷預測時需要根據具體情況確定隱含層的層數，且直接影響預測結果的準確性。若想提高預測精度，則要建立合理的BP 神經網絡結構。

1）輸入及輸出層節點數的確定。選取該區域內一個調度周期的歷史負荷數據，分析最大負荷時周圍環境情況，比如最低溫度、最高溫度及天氣情況，確定輸入層和輸出層的節點個數。

2）隱含層層數的確定。隱含層層數的增加雖然可以提高信息處理能力，但會使得整個網絡結構變得復雜，影響樣本的訓練速度。在進行短期電力負荷預測時，選取一個隱含層即可以滿足預測精度，也可通過增加網絡節點數的方法提高網絡處理能力。

3）隱含層節點數的確定。在不同的情景下，確定不同隱含層節點個數。通常情況下，為使網絡預測精度更高，可增加隱含層節點個數，但是節點個數越多，樣本訓練時間越長。因此，采用試湊法進行多次訓練以確定隱含層節點數。

3 算例分析

應用BP 網絡神經算法建立負荷預測模型，以某區域2020 年某典型日負荷曲線為例進行預測分析。算例中最大訓練步數為8 000，效率因子選取為0.1，目標誤差選取為0.001。通過神經網絡進行訓練，得到誤差曲線。對已經訓練的網絡設定訓練步數，檢驗算法的預測性能并進行對比分析。

經過樣本數據訓練得到該地區典型日24 小時內實際值與預測值的對比，如圖4所示。從圖4中可以看出，預測值與實際值較為接近，其誤差曲線如圖5 所示。從圖5 中可以看出，最大相對誤差為260 MW，最小相對誤差為20 MW。

圖4 實際值與預測值對比

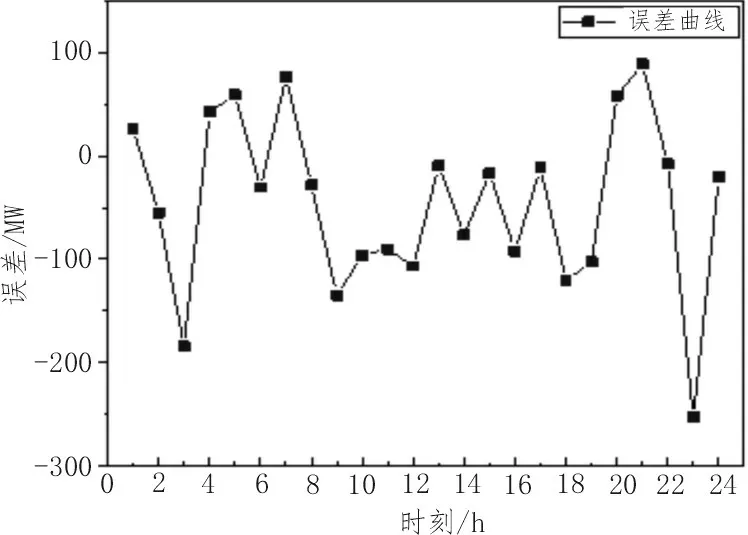
圖5 誤差曲線圖

為進一步體現該文方法的有效性，分別采用3種方法對該地區進行短期電力負荷預測，并進行總結比較分析，結果如表1 所示。從表中可以看出，當采用BP 神經網絡進行預測時所得到的平均誤差最小、收斂速度最快且預測精度較高。

表1 算法對比分析

4 結論

該文主要研究了基于BP 神經網絡算法的短期電力負荷預測，首先對BP 神經網絡算法的原理進行介紹；其次詳細闡述短期電力負荷的預測流程，將S型函數的負荷數據歸一化至0～1 之間并進行數據歸一化處理；最終應用BP 網絡神經算法建立負荷預測模型，以某區域2020 年某典型日負荷曲線為例進行預測分析，并檢驗算法的可行性。為進一步體現文中方法的有效性，設置3 種方法對該地區的負荷進行短期電力負荷預測。通過對比分析可知，當采用BP 神經網絡進行預測時所得到的平均誤差最小、收斂速度最快且預測精度較高。由于在預測過程中，天氣、氣候等因素會影響預測結果，下一步將研究考慮多種不確定因素的短期電力負荷預測方法。