雙層微納結構增強電磁屏蔽的機理分析與驗證
廖敦微,鄭月軍*,崔 浩,2,寸 鐵,付云起
(1.國防科技大學 電子科學學院,湖南 長沙 410073;2.沈陽飛機設計研究所,遼寧 沈陽 110000;3.中為聯合創新(平潭)工程研究有限公司,福建 福州 350000)
1 引 言
作為一種網格型透明導電薄膜,金屬微納結構具有高透光性[1-4],其光學性能主要通過結構的周期和線寬尺寸進行調節。與其他傳統連續透明導電薄膜相比,金屬微納結構的周期遠大于可見光波長,又遠小于微波波長,因此同時具備高透光和電磁屏蔽性能[5]。通過在透明基底上制備圖案化的微納結構,不同的金屬圖案結構和尺寸,呈現出不同的光學和電磁屏蔽性能,金屬微納結構在透明電磁屏蔽領域備受重視。
在透明電磁屏蔽領域,透明導電薄膜要具有較高的光學透過率[1,4],且在所需微波頻段能夠產生良好的屏蔽性能[5]。金屬微納結構與傳統的ITO透明導電薄膜相比具有透光率高、柔韌性強以及尺寸參數可靈活調節的優點,但透光率與電磁屏蔽性能不能兼顧[4-5]。為了解決上述問題,科研人員采用結構優化的方法,通過不同圖案結構的性能對比發現,雖然結構優化[6-7]在相同透光率下能提高電磁屏蔽性能,但性能提升效果并不明顯。由此可知,在單層微納結構基礎上僅改變微納圖案結構及尺寸難以顯著提升透光率和電磁屏蔽性能,因此,科研人員開始聚焦雙層/多層微納結構的研究[8-14]。
國外最早研究雙層微納結構并應用于紅外濾波[8],隨后我國學者將雙層微納結構應用于透明電磁屏蔽[9-10,13],并通過研究發現雙層微納結構在相同透光率前提下能提升屏蔽效能,這引起了科研人員的興趣。圍繞雙層微納結構眾多學者展開了卓有成效的研究,提出并設計了雙層方格微納結構[9-10]、雙層圓環微納結構[11]、方格和圓環混合雙層微納結構[13]以及多層微納結構[14]等,取得了良好的光學和電磁屏蔽性能。但是,目前的研究大多是通過結構設計在相同透光率下增強電磁屏蔽性能,鮮見對其電磁屏蔽增強的作用機理研究。
本文以方格結構為例分析了雙層微納結構的增強電磁屏蔽效能的機理,推導出雙層方格型微納結構電磁屏蔽的理論計算公式,并與全波軟件仿真結果進行了對比,驗證了機理分析的正確性。該電磁屏蔽增強機理分析與理論計算公式可擴展到多層微納結構,具有通用性。制備了的雙層方格微納結構透明導電薄膜樣品,通過實測進一步驗證了電磁屏蔽增強機理的有效性。
2 理論分析及模型建立
2.1 單層微納結構理論分析
1964年,Vogel等提出了一種方格微納結構[15],并在遠紅外波段對它進行了透射和反射性能研究。1967年,Ulrich首次在理論和實驗上給出了金屬微納結構及其互補結構的光學特性并用傳輸線等效電路進行了描述[16]。在Ulrich模型的基礎上,研究人員又對微納結構的等效模型進行了補充分析和研究[17-18]。1993年,Kohin,Margaret等基于Ulrich的電路模型給出了微納結構的歸一化導納公式,以及由此得到的微波透過率公式,并且進行了相應的近似和簡化,這方便了對微納結構的分析和計算推導[19]。
微納結構理論分析一般以方格結構為例,其總透光率等于所有光學衍射級透過率的總和,可以采用遮攔比對總透光率近似表示[1]:

其中:2a是線寬,g是微納結構周期。由此可知,對線寬和周期尺寸進行優化可提升透光率。
單層微納結構作為一種感性導納結構在電磁波垂直入射時的透過率近似表示為:

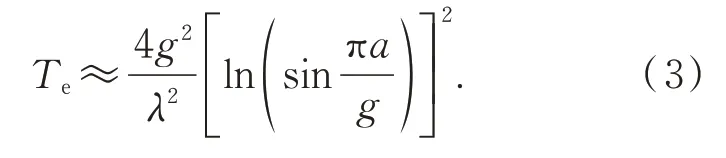
將透光率公式和微波透過率公式化簡合并,可以得到透光率和微波透過率之間的關系:

由式(4)可知,單層微納結構的微波透過率與透光率之間成正比關系,即在結構尺寸一定的情況下,透光率越高,微納結構的微波透過率也越高,即電磁屏蔽性能越差,透光率與電磁屏蔽性能之間相互制約。
2.2 雙層微納結構等效分析模型
本文引入雙層微納結構以提高屏蔽效能,雙層結構的等效電路如圖1所示。在兩個并聯電感之間有一段傳輸線。

圖1 雙層微納結構示意圖及等效電路Fig.1 Schematic diagram and equivalent circuit of double-layer micro-nano structure
雙層微納結構由兩個單層微納結構和一定厚度的透明介質支撐結構組成。由于單層微納結構在等效電路中相當于感性導納結構,考慮到一般情況,上下兩個端口都為空氣介質,中間支撐層為相對介電常數為εr的一般透明介質,因此其等效電路為兩個并聯導納之間串接了一段傳輸線。相對于波長,雙層微納結構的間距較近,因此這是一段緊耦合傳輸線,兩個單層網柵之間會產生強烈的耦合作用。
3 電磁屏蔽增強機理分析
設雙層微納結構間距為d,轉化成電長度,得到其傳輸(A B C D)矩陣關系式如下:

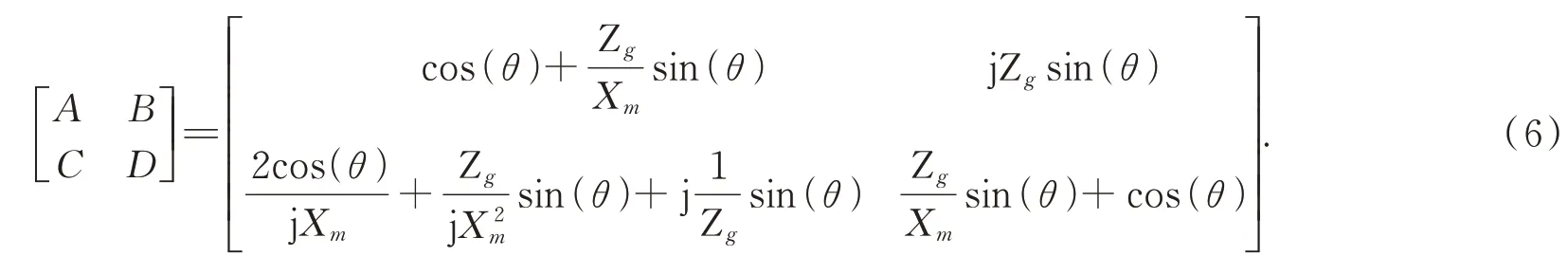
代入到歸一化矩陣中得到參數S,其中S21的 表達式為:

利用透射系數推導得到雙層微納結構的電 磁波透射率為:

由雙層微納結構透射推導機理可知,雙層微納結構層與層之間的間距與電磁透射率密切相關,且這一微納結構透射機理可推廣至三層乃至多層微納結構,具有通用性。
4 計算仿真分析與實測結果
4.1 計算與仿真分析
為驗證上述雙層微納結構公式用于電磁屏蔽增強機理分析的正確性,鑒于鎳金屬相對于襯底具有良好的黏附力,因此設計了一種銅鎳合金的雙層方格形微納結構。而PET介質作為一種常見的柔性透明襯底材料和金屬嵌入介質的考慮,在本文中采用PET透明介質作為雙層微納中間隔離層。為了增強結構穩定性,減少金屬與空氣之間的接觸提升微納結構的抗氧化能力,將金屬結構齊平嵌入到PET介質中,如圖2所示。從圖中可以看出,該雙層微納結構為方格型周期結構,在尺寸參數普適性的基礎上,基于仿真計算分析和方便制備的角度出發,選用周期g=120μm,線寬2a=10μm,結構厚度t=2μm,PET介質厚度為h=100μm。將結構參量代入理論計算公式計算方格型雙層微納結構的電磁屏蔽性能,并與單層微納結構的電磁屏蔽性能進行了對比,同時在軟件CST中對方格型雙層和單層微納結構建模進行全波仿真,結果如圖3所示。單層和雙層微納結構的理論計算和仿真結果吻合較好,其中的細微差異是由于微納結構計算是假定金屬厚度很薄的情況下推導出的近似公式而實際仿真模型有一定厚度導致的。由于在全波仿真中微納結構比計算對應波長小2~3個數量級,理論計算結果與全波仿真結果相互驗證對方結果的正確性。

圖2 雙層方格型微納結構Fig.2 Double-layer square micro-nano structure
從圖3還可以看出,在2~18 GHz,雙層方格型微納結構的電磁屏蔽性能比單層方格型微納結構高15 d B左右,驗證了雙層微納結構具有電磁屏蔽性能增強的作用。通過上述分析可知,進行雙層或多層設計可解決單層結構透光率與電磁屏蔽之間性能制約的矛盾。
進一步,在微納結構周期、線寬和金屬厚度不變的情況下,分析了PET厚度對方格型雙層微納結構電磁屏蔽性能的影響,PET厚度從50 μm增加到250μm,分析結果如圖4所示。從圖中可以看出,隨著PET厚度的增加,即雙層微納結構之間的距離越大,電磁屏蔽性能越好,但是厚度增加得越大,電磁屏蔽性能增大的變化率越小。由此可知,考慮透光率,PET厚度不是越大越好。

圖3 雙層網柵與單層網柵的屏蔽效能計算和仿真結果對比Fig.3 Comparison of shielding effectiveness calculation and simulation results between double-layer and single-layer grids

圖4 不同PET厚度下雙層微納結構屏蔽效能的仿真結果Fig.4 Simulation results of shielding effectiveness of double-layer structure under different PET thicknesses
4.2 實測驗證及結果對比分析
為進一步驗證機理分析和全波軟件仿真結果的正確性,制備了雙層方格微納結構樣件,如圖5所示。從圖中較清晰地看到覆蓋的NUDT的字樣,展現了較好的透光性能。

圖5 雙層微納結構實物樣件Fig.5 Sample of double-layer micro-nano structure
采用光譜儀測試了樣件的透光率,結果如圖6所示,在400~700 nm的可見光波段,樣品的平均透光率為71%。在微波暗室采用雙天線法測試了樣件的屏蔽效能,并與理論計算結果進行對比,如圖7所示。從圖中可以看出,測試結果與理論計算結果基本一致,在2~18 GHz的屏蔽效能大于45 dB,其中存在的細微誤差是由樣件每個角的加工誤差所致。由測試結果可知,樣件具有良好的透明屏蔽性能。

圖6 雙層方格型微納結構的透光率測試結果Fig.6 Measured light transmittance test result of doublelayer square micro-nano structure

圖7 雙層方格微納結構電磁屏蔽效能的測試與仿真結果Fig.7 Electromagnetic shielding effectiveness test and simulation results of double-layer square micro-nano structure
5 結 論
本文分析了方格型雙層微納結構電磁屏蔽的機理,推導出屏蔽效能的理論計算公式,這一理論計算公式可推廣至多層微納結構,具有通用性。將理論計算結果與全波仿真結果進行了對比,驗證了機理分析和全波仿真軟件分析的正確性。最后加工了樣件進行測試,樣件的實測結果與理論和全波仿真結果基本一致,在2~18 GHz內屏蔽效能大于45 d B,平均透光率超過了71%,樣件具有良好的透明屏蔽性能。本文的機理分析為多層微納結構設計提供了理論支撐。

