狹長空間火災煙氣傳輸的準穩態時間模型

狹長空間作為建筑結構中一種常見形式，在長度方向上的尺度遠大于高度和寬度，如地下人行通道、建筑走廊、帶垂壁的頂棚等.對于此類結構的火災安全而言，火災早期煙氣傳輸行為特性及其射流發生后的羽流溫度、速度傳輸特性是火災探測器和自動滅火系統安裝的主要依據，也是相關消防系統設計、安裝規范與標準的基礎，具有重要的理論和工程應用意義.

Delichatsios等針對由垂壁頂棚形成的狹長空間中的火災煙氣傳輸行為開展了實驗和理論研究，結果表明，垂壁或側壁的存在對煙氣頂棚射流后煙氣蔓延過程產生重要影響，煙氣羽流速度、溫度等分布特性與開放空間中的明顯不同.此后，有關狹長空間火災煙氣傳輸特性的研究一直成為建筑、土木等相關領域火災安全研究的熱點之一.在火災早期，由于火源功率較小，煙氣從火源蔓延到頂棚上目標處(如探測器安裝位置)需要一定的時間，即煙氣羽流傳輸延滯時間，這會造成目標位置處溫度和速度分布等煙氣特性響應延滯，也是發展火災探測器探測時間預測模型所需要解決的至關重要的問題.為此，針對開放空間火災，Heskestad等對火(為時間)情況下煙氣延滯時間開展了實驗和理論研究，發展了煙氣延滯時間的無量綱方程，即開放空間平整頂棚煙氣蔓延延滯時間關系式，隨后被Beyler在求感溫探測器響應時間解析解時加以運用，并被吸納應用于至今仍在廣泛使用的感溫火災探測器時間計算模型DETACT-T2中.隨著火災增長，當火災熱釋放速率到了一定規模，達到準穩態，即相對于火源熱釋放速率的變化時，頂棚目標位置處的煙氣速度、溫度等變化也即刻響應，從而可以忽略煙氣傳輸延滯效應對煙氣羽流、速度縱向分布帶來的影響，文獻[19]中給出了準穩態假設成立的判別關系式.可以看出，與開放空間火災類似，狹長空間中火災煙氣傳輸同樣存在煙氣延滯行為及準穩態過程，其準穩態模型是火災探測器響應時間計算和模型建立的基礎，相關研究鮮有報道.

在圖2模擬電路的基礎上，將第一級反轉電容從50 nH改為12 nH，負載阻抗隨之升高，變為60 Ω。同時，監測A點的電壓，模擬結果如圖4所示。

各級導線點宜施測圖根級水準高程，高等級導線(如一級導線)沿主要道路布設，沒有管線的地區則不必布設控制點，次要道路加密二級或圖根級導線。以此為基礎在全測區加密圖根水準。

本文針對狹長空間火災早期煙氣傳輸延滯行為開展理論研究，提出煙氣傳輸延滯時間的計算方法，并建立非穩態火源情況下狹長空間煙氣傳輸中準穩態假設成立的臨界時間模型，為后續發展狹長空間火災探測器布置方法、消防設計等提供理論依據.

所使用的日降水量數據來源于2001—2016年臨安國家基本站觀測數據,以20時為日界,日降水量≥50 mm為一個暴雨雨日。本文中的季節劃分方式如下:春季為3—5月,夏季為6—8月,秋季為9—11月,冬季為12月—次年2月。

1 狹長空間火災煙氣傳輸的準穩態時間模型

1.1 狹長空間火災煙氣傳輸模式

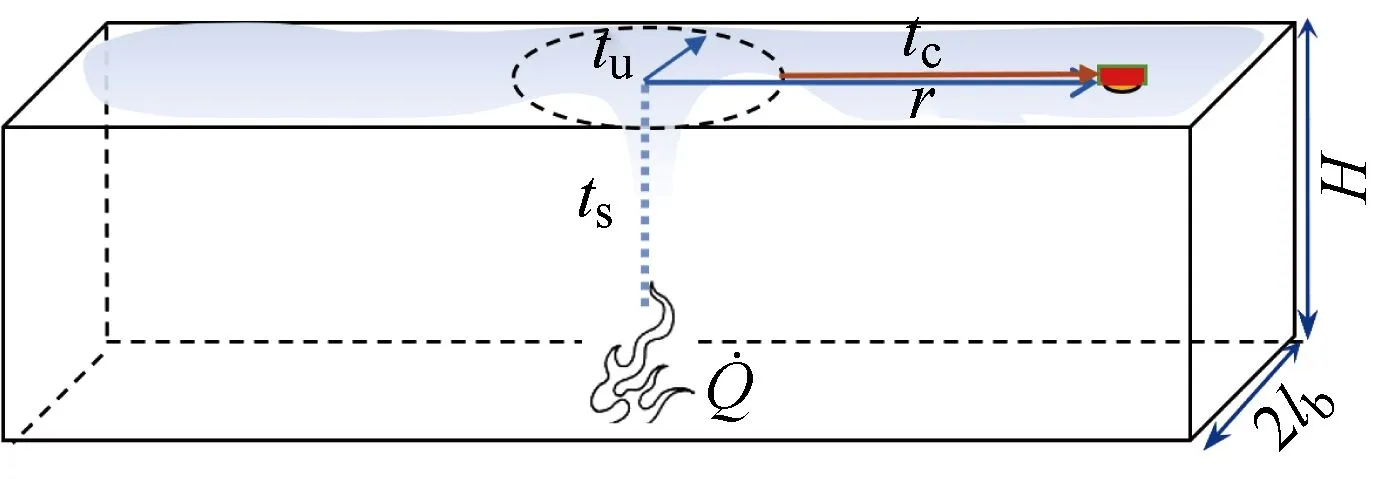
1.2 狹長空間穩態火源煙氣的傳輸時間計算

煙氣從火源產生并蔓延至頂棚目標位置的時間即為熱煙氣傳輸到目標位置的時間：

精神類藥物 抗抑郁藥和吩噻嗪類抗精神病藥包括奮乃靜、氯丙嗪、丙咪嗪、丙氯拉嗪、三氟拉嗪、地昔帕明等，服用后都易出現光敏性皮炎。

=++

(1)

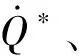
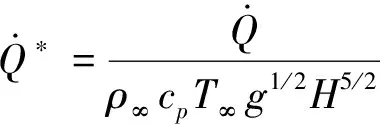
(2)

(3)

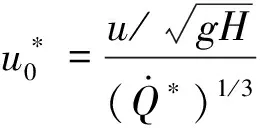
(4)

式中：為空氣密度；為空氣比定壓熱容；為初始環境溫度；為重力加速度；和分別為距離羽流撞擊點處煙氣的流速和溫度；Δ為溫升，計算式為Δ=-

..上升時間 在火災早期，火源功率較小，火焰高度相對于頂棚高度可以忽略，因此可采用弱羽流理論中的點源假設，有關理論參考文獻[19]，羽流中心線上的速度計算如下：

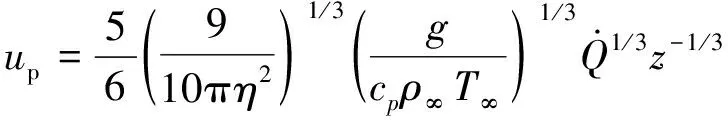
(5)

式中：為常數，一般取值0.15；為火源上方垂直高度.

于是，羽流自火源上升至頂棚所需時間為

(6)

結合式(22)，可得Karlsruher增長型火災煙氣傳輸滿足準穩態的條件為小于臨界縱向距離：

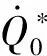
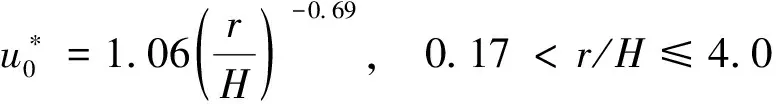
(7)

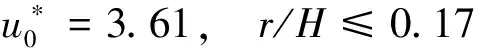
(8)

結合式(4)可以計算從頂棚羽流撞擊點沿縱向處的煙氣流速：

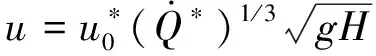
(9)

妊娠和分娩對女性機體是一個較大的應急事件，妊娠時的飲食、運動量、血壓及體質管理都關系到母嬰的結局，產后生殖器官(乳房外)需恢復到非孕狀態，產婦身體虛弱，抵抗力差，同時又面臨著哺乳、育兒，形體的恢復等一系列的問題，這個時期健康教育指導對孕產婦是至關重要的[4]。本研究對圍產期孕產婦實施全程個體化系統管理模式，即從孕前、孕早期、妊娠期、分娩期直至產褥期包括新生兒的護理，實施個體化的系統管理。

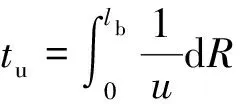
(10)

式中：為積分變量，∈(0,)

..縱向蔓延時間 煙氣沿頂棚蔓延至頂棚下的遮擋物或走廊兩側墻壁，其蔓延過程受限.Delichatsios通過實驗和理論分析，發展了沿狹長空間縱向煙氣流速隨無量綱距離呈指數衰減的關系式.隨后國際上多位學者對此方程進行了進一步研究和修正，Oka等在此基礎上通過進一步實驗和理論研究，建立了狹長空間火災煙氣傳輸中發生“水躍”前后的煙氣縱向速度衰減方程：

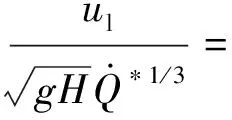
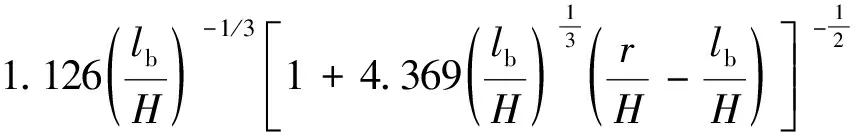
(11)

≤1523

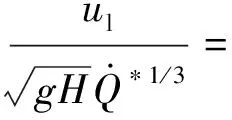
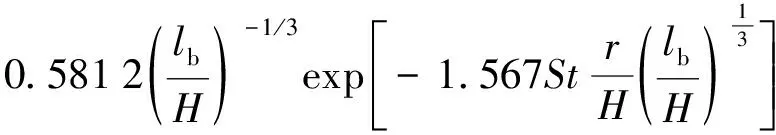
(12)

>1523

式中：為煙氣水平流速；為Stanton數，本文中取 0.015 13.

需要提及的是，狹長空間較多的情況是/<0.2，“水躍”現象發生在煙氣碰撞側壁面之后.于是，煙氣受壁面或橫梁影響，結合式(11)和(12)，沿縱向蔓延至處的時間依據下式進行計算：

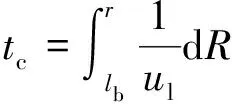
(13)

1.3 非穩態火源情況下煙氣傳輸延滯時間計算方法

給定，，，設置初始時間為0，時間增量Δ，將時間離散為=Δ，=Δ，計算時長=Δ(為正整數，盡可能取大).

于是，煙氣從羽流撞擊點蔓延至墻壁面的時間可按下式計算：

高速公路經營管理單位崗位工種相對單一，人才成長通道相對狹窄，現有基層站區長工作經歷一般比較簡單，缺乏崗位鍛煉。加之跨行業業務交集少、交流互動少，培訓學習內容比較專業，導致基層站區長視野不開闊，溝通能力弱，能力提升慢，缺乏處置復雜問題的經驗積累。

1.4 延滯時間的無量綱模型

已有研究表明在火災初期階段的火災熱釋放速率增長規律主要有下面兩類.

(1)Heskestad研究建議火災增長初期的熱釋放速率大體與時間呈冪指數增長規律，與實驗數據吻合較好，以下稱Heskestad型火災.

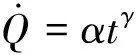
(14)

式中：為火災增長系數；為正指數，通常取2，因而也經常稱為火.

(2)德國卡爾斯魯厄大學火災研究所在大量室內火災實驗的基礎上，總結出如下熱釋放速率發展關系式，以下稱Karlsruher型火災.

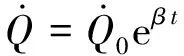
(15)

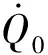
對于火，文獻[26]研究得到了煙氣延滯時間的工程模型：

=

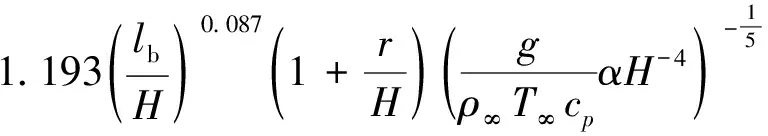
(16)

下文將針對Karlsruher型火災下，狹長空間煙氣延滯時間進行無量綱分析.從火災動力學理論分析，煙氣傳輸的延滯時間受諸多參數影響，表示為如下多參數的函數關系：

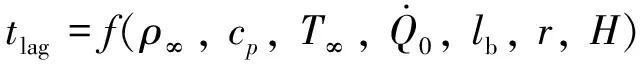
(17)

根據相似理論，對上式進行無量綱化處理：

另一方面，校園文化更像是對社會文化在進行某種過濾。社會文化過于紛雜，校園文化對其進行吸收的同時，取其精華去其糟粕，將那些不適合自身的文化因素舍棄掉，將那些適用于自身的拿過來，并且進行本地化，這是一種對于社會文化的認同與超越。但是同時，高職院校以自身文化培養出來的人才，不斷在向社會進行輸送，靠著這些人才，以自身的形式，對社會文化進行影響與改變。所以說，校園文化與社會文化之間，是一種對立統一的關系。

(18)

上式中的各無量綱參數定義如下：

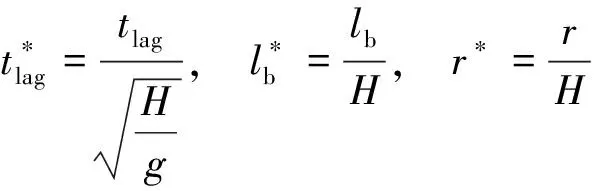
在上述公式中，a 表示為(1,10)之間任意常數；n 表示為輸出；m 表示為輸入；l 表示為節點。在預測和分析模塊中，輸入層的節點包括ID、數值、類型、人員性質、現狀、有無疾病史等8 個屬性。所以網絡的輸入層m=8；根據預測和分析要求，將分析結果作為網絡輸出結果，因此輸出層節點n=1；由于三層BP 神經網絡可接近任意連續的函數，故選擇BP 三層網絡。同時根據輸入層、輸出層和隱藏層的個數，經試驗，可以得到每個隱藏層節點個數為5。

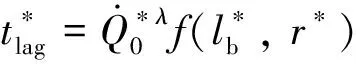
(19)

根據式(4)定義的無量綱速度以及式(18)定義的無量綱時間和長度可得：

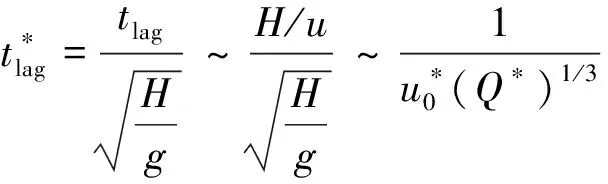
即=-1/3，于是得

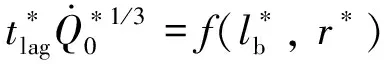
(20)

為了得到解析關系，根據相似理論，建立如下指數關系式：

(1)編碼：根據實際線路的站臺數，將列車在各站的停站時間序列D=[D1,D2,D3,…,Di,…，DN]和發車間隔H=

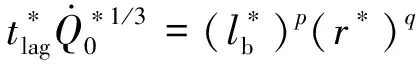
(21)

式中：和為待擬合系數.通過設計不同火災場景(見表2)，根據1.3節的計算方法對延滯時間進行計算.為了方便對式(21)中3個無量綱量數群進行擬合，先將方程兩邊進行對數化處理，再根據表2中數據，通過線性擬合分析，進一步得到和的值分別為 0017 8 和 1249 3，擬合優度為099，表明相關度高，再代入式(21)得到如下關系式：

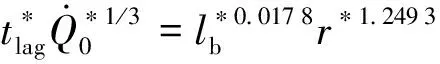
綜合式(18)和(21)得到煙氣延滯時間計算式：

=

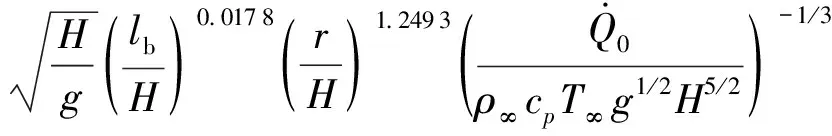
(22)

1.5 準穩態假設適用的時間模型

當火災成長到一定規模，其火源熱釋放速率的變化引起頂棚目標位置的煙氣特性參數變化，可以認為是瞬態響應的，即火源達到了準穩態.Alpert指出，穩態火源下的煙氣特性關系式應用于非穩態火源需要滿足準穩態假設，即

對不同時刻所產生的煙氣延滯時間()進行統計，其最小值即為煙氣延滯時間值.

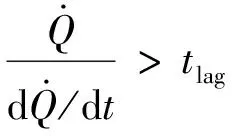
(23)

(1)要點探究。彰顯生產力進步，在現代化企業管理模式中的地位，進一步詮釋企業發展，增進企業之間聯系的有效措施。簡單來說，企業管理環節的“生產力”，是指能夠促進企業發展的計劃，也是企業發展中的先進企業文化，增強現代企業內部資源調控的價值。

將式(14)代入式(23)并整理得：

>

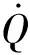
(24)

結合式(16)，即得Heskestad型火災煙氣傳輸滿足準穩態假設的臨界時間為

=

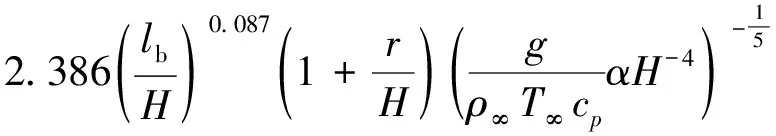
(25)

同樣，將式(15)代入式(23)并整理得：

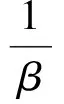
(26)

..徑向蔓延時間 頂棚射流之后，熱煙氣將貼頂棚下壁面徑向蔓延，Alpert發展了如下無量綱關系式：

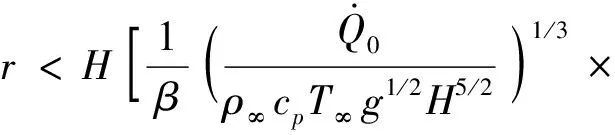
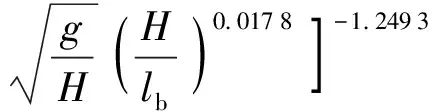
(27)

即對于Karlsruher增長型火災，狹長空間中煙氣傳輸的準穩態僅存在于臨界縱向距離內，而之外的區域無法達到臨界狀態.

綜上所述，對于Heskestad和Karlsruher型火災，當式(25)和(27)分別成立時，滿足火災準穩態條件，可以忽略煙氣流延滯效應，近似認為火源的變化立即引起目標位置附近煙氣速度、溫度等參數的瞬態響應.

2 計算與分析

為了表明上述理論模型的應用，假定火源為中速發展火，= 0.011 7 kW/s，狹長空間=4 m，橫梁(或走廊)半寬為1 m，=3 m，初始環境溫度為20 ℃.根據上述理論模型對煙氣延滯時間進行計算，首先根據時間鏈法的計算步驟完成相關參量計算，不同時刻火源對應的煙氣延滯時間結果如圖2所示.需要說明的是，在煙氣到達目標位置之前，煙氣傳輸時間在計算結果上表現為較大的時間值，其實際的物理意義可解釋為早期火源功率小，煙氣在傳輸過程中由于卷吸空氣、黏性耗散、擴散等微相行為導致動能散失，同時因卷吸冷空氣而導致溫度降低，引起熱浮力的衰減，從而煙氣在傳輸過程中未到達目標位置而被后面的另一波高溫熱煙氣趕上并裹挾，在理論上表現為煙氣從火源位置傳輸到目標位置的傳輸時間計算值較大.

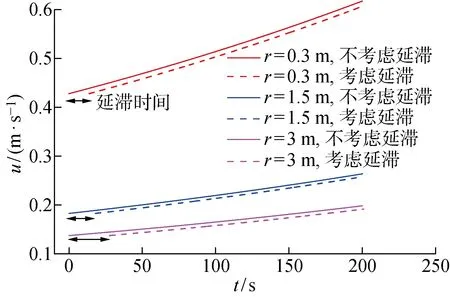
此外，隨著火災的發展(即火源功率增大)，不同時刻火源產生的煙氣傳輸時間逐漸縮短，此工況下的煙氣延滯時間為27.7 s，根據式(25)計算可得準穩態條件成立的臨界時間為55.4 s.將考慮煙氣延滯效應與不考慮煙氣延滯效應影響的煙氣分布特性進行了對比分析，圖3所示為在=3 m處的煙氣速度和溫度隨時間的變化曲線.在滿足準穩態假設后，煙氣延滯效應對煙氣的流速和溫度分布影響非常小，誤差約為5%～7%，工程上可以忽略不計.

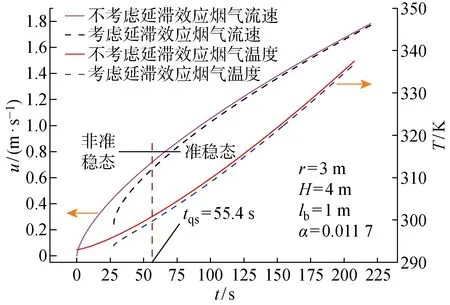
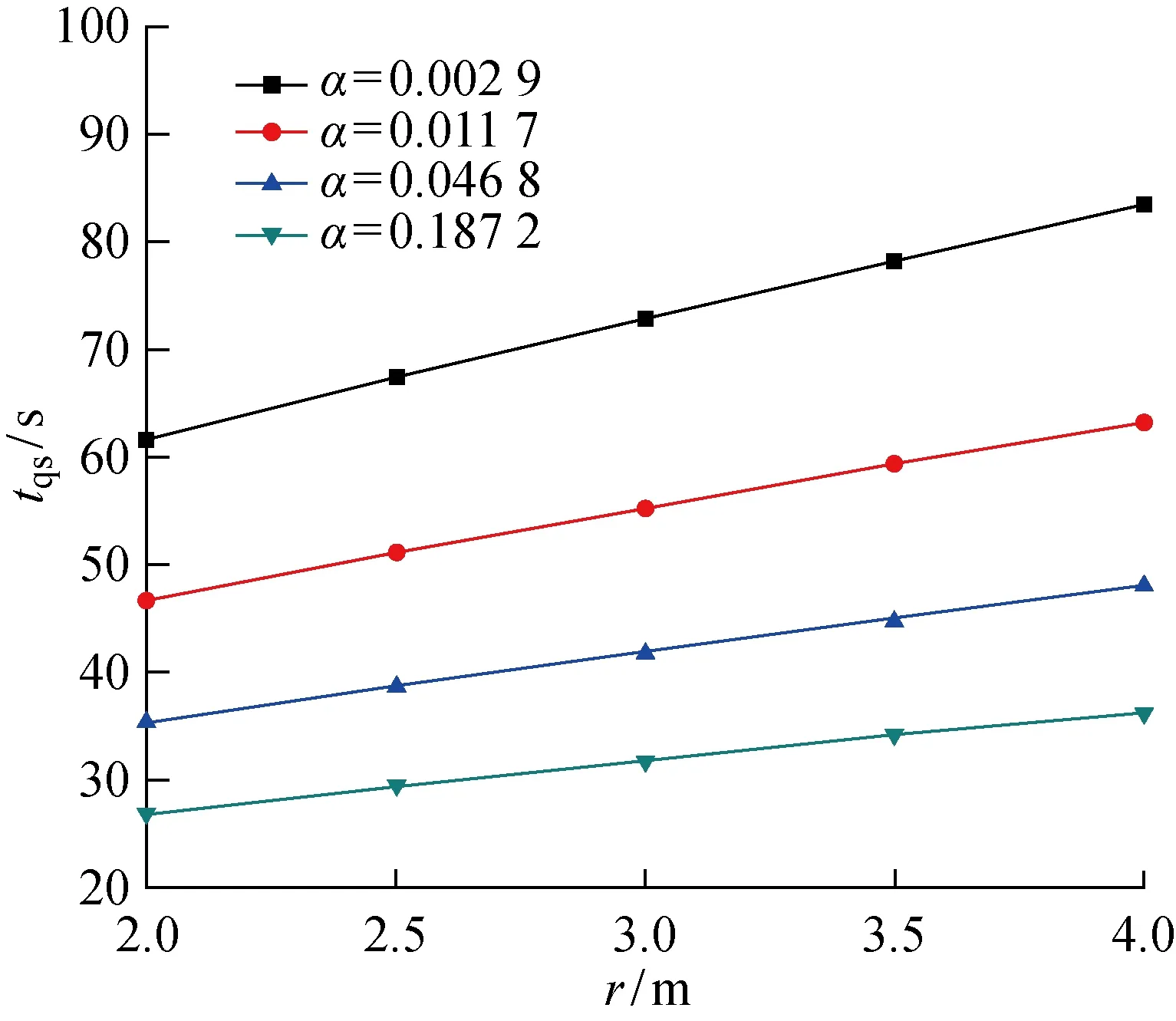
圖4所示為慢速、中速、快速及超快速火情況下不同處的.可以看出，隨著火災增長系數的增大，對應的臨界時間隨之縮短，且對于相同值，臨界時間與呈線性遞增關系，與式(25)一致.

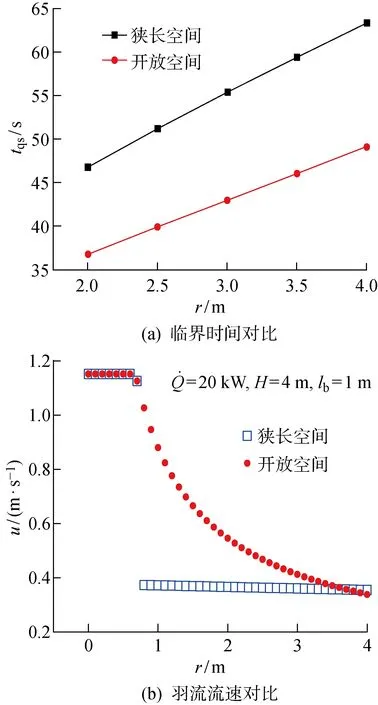
為了對比狹長空間和開放空間中煙氣傳輸準穩態假設條件成立的臨界時間之間的差異，改變值，分別進行計算，結果如圖5所示.其中，開放空間煙氣延滯時間計算式如下：

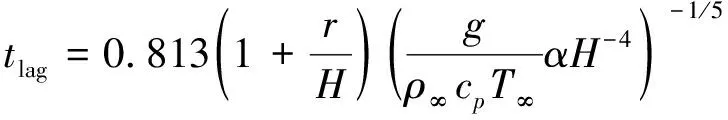
(28)

代入式(24)，即得到開放空間火災準穩態假設條件成立的臨界時間.

此外，國內學者對我國農村農戶信貸行為進行了許多相關的研究。其中，史清華（2002）5的研究認為戶主文化程度、戶主年齡、農戶家庭收入水平與農戶是否借貸等方面之間的存在密切關系。周小斌、耿杰（2004）6通過研究我國農戶借貸需求的影響因素，認為農戶的經營規模、農戶支付傾向和農戶投資能力對農戶借貸需求有正向作用，農戶自有資金支付能力對農戶借貸需求有負向作用；顏志杰（2005）7對全國范圍內的農戶進行了一次信貸相關的抽樣調查，以分析農戶信貸需求的影響因素，分析結果表明，消費、生產等多方面因素影響農戶信貸需求的因素；

3 結論

本文根據弱羽流理論和現有狹長空間煙氣頂棚射流的研究成果，從理論上建立了煙氣傳輸延滯時間模型，發展了煙氣延滯時間計算方法，建立了準穩態條件成立的臨界時間計算模型，并進行了相關計算和對比分析與討論，得到如下結論：

如圖6所示，造林密度與油松純林保存率呈現負相關關系。隨著造林密度的增加，油松純林的保存率下降，其回歸方程y=-0.006 2x+107.76，相關指數R2=0.968 9。表明低密度下油松個體間競爭小，油松能夠獲得正常發育所需的營養。另外密度過高還會增加病蟲害的爆發幾率，增大林分枯死率。

(1)相同工況條件下，狹長空間中的煙氣傳輸延滯時間比開放空間中的長.這是由于狹長空間中火災煙氣在發生頂棚射流后遇到側壁阻擋，羽流轉向沿縱向蔓延，其煙氣流速較開放空間情況下的值小，傳輸中卷吸冷空氣而降低了溫度，引起熱浮力的衰減，從而導致流速迅速降低.

(2)與開放空間相比，狹長空間中頂棚給定縱向距離處的煙氣傳輸達到準穩態的臨界時間比開放空間中的值大，這是由于狹長空間中的煙氣傳輸延滯時間比開放空間下的值大.

觀察兩組患兒并發癥的情況，其中包括：肝內膽管擴張、術后膽管炎、門脈高壓癥，總發生率=發生例數/總例數×100%。

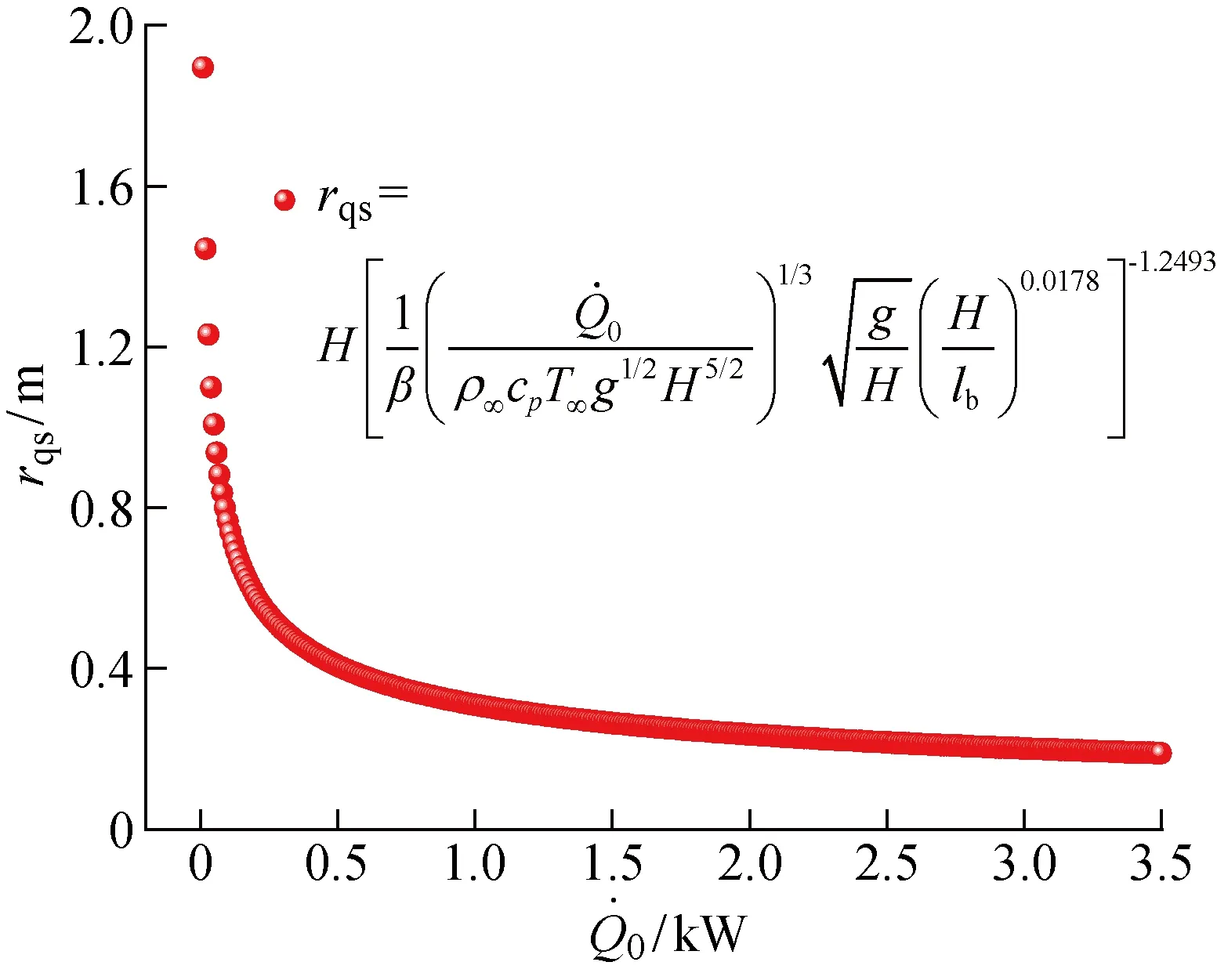
(3)對于Karlsruher型火災，從理論上建立了狹長空間煙氣延滯時間計算的無量綱模型.臨界縱向距離隨著初始火源熱釋放速率的增大而急劇衰減.當初始火源熱釋放速率大于3.5 kW時，火源將無法達到準穩態.當初始火源熱釋放速率較小時，準穩態在羽流中心線縱向距離約為1.9 m范圍內成立.