基于統一強度理論的螺紋樁承載力計算方法

螺紋樁是一種由樁芯和連續螺牙組成的異形截面樁，因形似螺絲釘而得名.其前身包括螺旋鋼樁(螺牙為分離式，一般為1～3片)、預制螺紋樁、Atlas 樁等，最初由吳敏等借鑒國外相關樁型設計而成，具有良好的承載性能.

近年來，螺紋樁憑借其承載力高、沉降較小、施工效率高、經濟環保等優點在房建及交通工程基礎設施建設領域中得以廣泛使用.然而，目前關于螺紋樁承載機理的研究卻主要集中在數值模擬、模型試驗及現場試驗等方面，傾向于從宏觀角度分析螺紋樁承載機理.李成巍等通過模型試驗和數值分析，研究了螺紋樁的豎向承載機理，發現影響螺紋樁豎向承載力的關鍵因素為土體抗剪強度指標、螺距及螺牙高度.王國才等通過Abaqus對螺紋樁豎向承載特性及影響因素進行研究，發現螺紋樁極限承載力隨(為螺距，為外徑)先增大后減小，并在處于0.5～2時達到最大值.孟振等通過室內模型試驗對比分析發現在相同條件下，螺紋樁的極限承載力約是普通樁極限承載能力的1～4倍，而蔣鵬程發現螺紋樁極限承載力比普通樁單樁提高了67%.

在螺紋樁極限承載力計算方面，常規方法仍以混凝土圓樁承載力計算方法為基礎進行適當修正，主要包括將螺紋樁極限側摩阻力乘以一定放大系數、將樁土極限側摩阻力替換為土體抗剪強度或者將螺紋樁簡化為多支點的摩擦端承樁等.這類方法忽略了螺牙與樁間土的局部相互作用，承載機制不清的同時阻礙了計算精度的提高，易造成工程實踐浪費或安全隱患.因此，若要實現螺紋樁承載力的準確計算，必然要明確螺牙與樁間土的相互作用規律，嘗試基于解析手段揭示螺紋樁的承載機理.

綜合當前國外螺紋樁破壞機制的研究成果可以發現，關于螺紋樁破壞機制的研究尚不多見，且主要集中于螺紋樁的前身螺旋鋼樁.有關螺旋鋼樁的研究最早開始于20世紀60年代，已提出了多種破壞模型：葉片支撐破壞模型、圓柱破壞模型、單層葉片對數滑裂面破壞模型等.然而，螺紋樁在構造特點上與螺旋鋼樁具有較大差異，相關理論的普適性尚有待商榷.國內關于螺紋樁破壞機制的研究處于起步階段，目前關于這方面的報道為數不多.董天文等認為樁受荷載后樁頂處螺牙下方地基出現壓密區，繼而壓密區向外擠出產生滑裂面，最終形成梨形滑裂面破壞區，螺牙端阻力達到極限；繼續加載則螺牙間土柱被剪切破壞，下級螺牙開始承載，直至整個樁體發生破壞.孟振提出極限荷載下螺紋樁的兩種破壞模式，即“單獨承載破壞”與“圓柱形剪切破壞”，并分別討論了兩種模式下的承載力計算方法及破壞模式的判別方法.

然而，上述理論計算方法采用的屈服準則一般為單切應力屈服準則——Mohr-Coulomb(M-C)屈服準則，忽略了中主應力對土體屈服與破壞的影響既有研究表明，往往對材料的強度起到提升作用，而M-C屈服準則推導的地基承載力顯然不能反映地基實際情況，結果偏于保守，具有一定不足.

鑒于此，本文擬基于雙剪統一強度理論，以太沙基極限平衡理論為基礎提出螺紋樁的承載力計算公式，通過工程實例驗證計算公式的準確性及適用性，進而討論了統一強度理論參數(該參數反映了中間主切應力對材料屈服的影響)及螺紋樁關鍵參數對螺紋樁承載力的影響，以期進一步完善螺紋樁承載理論體系.

1 雙剪統一強度理論的M-C表述

雙剪統一強度理論數學表達式為

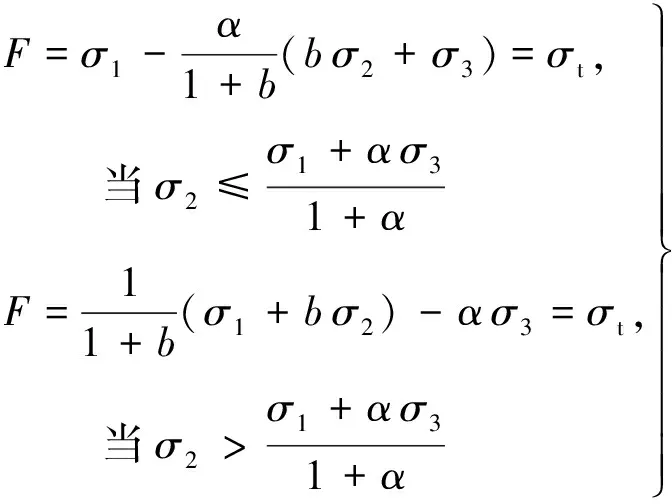
(1)

根據既有研究，當采用土體黏聚力與內摩擦角作為基本參數時，可轉換為M-C屈服準則形式：

假定螺紋樁穿過層土體，第層土體厚度為，內摩擦角及黏聚力分別為t、t，重度為，則螺牙產生的豎向承載力之和為

=+tan

其中：、分別為屈服面上正應力與切應力；、分別為統一黏聚力與統一內摩擦角.

該準則具有與M-C屈服準則同樣的表達形式，卻可以合理考慮中主應力效應.極限平衡狀態時計算表達式為

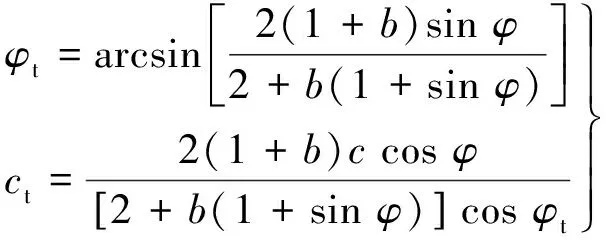
(2)

2 螺紋樁承載力推導

2.1 極限平衡理論及假定

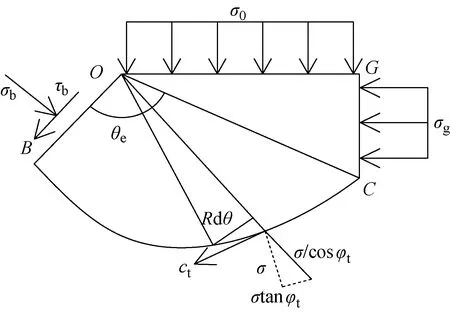
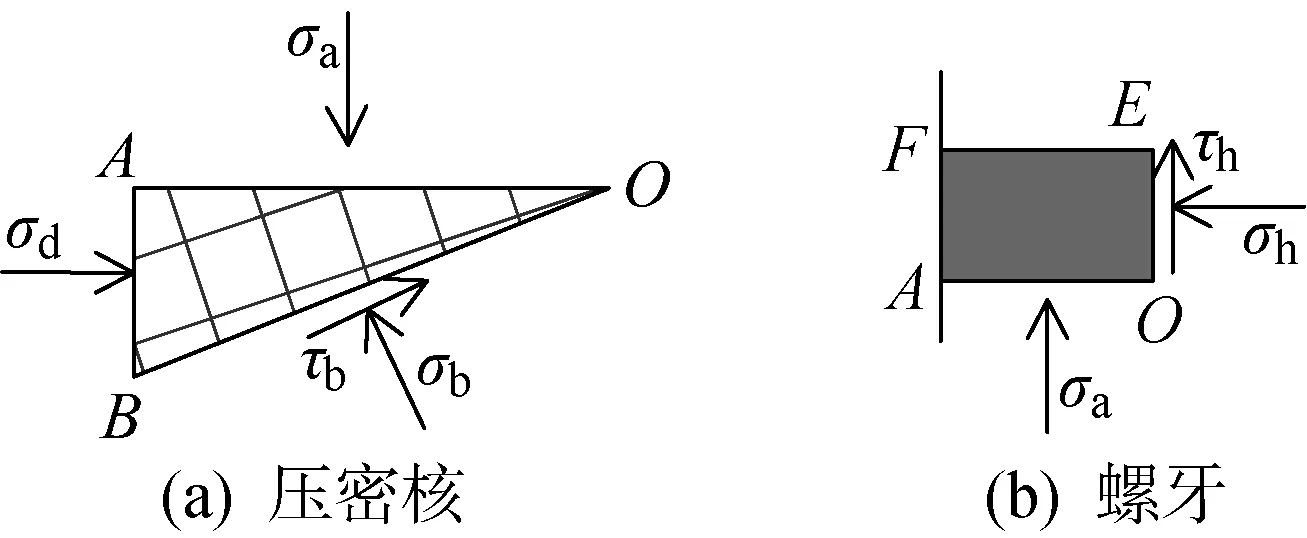
對于單獨承載破壞模式的螺紋樁，根據太沙基地基極限承載力計算方法，螺牙下土體分為3個區域，如圖1所示.圖中：面為螺牙底部；面為螺牙頂部；π4-2為朗肯被動狀態區面與水平面的夾角；為面上的均布壓力3個區域包括彈性壓密區、輻射向剪切區、朗肯被動狀態區，曲線為對數螺旋曲線，形式為=etan ，其中為旋轉半徑，為初始半徑，為旋轉角.本文在推導螺牙極限承載力時，基于太沙基極限平衡原理的假定，同時結合工程實際對計算模型進行了一定的簡化，作出如下假定：

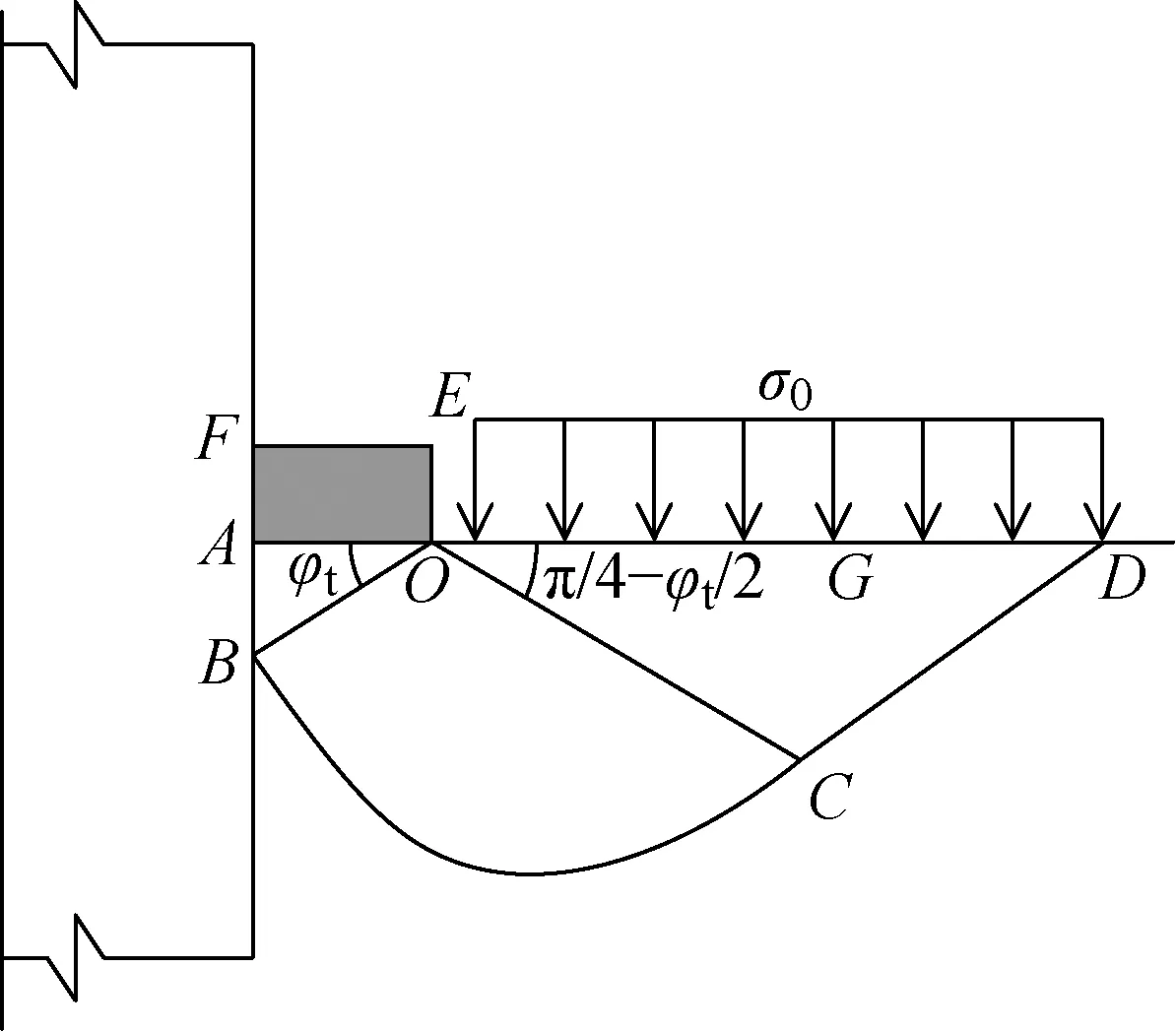
(1)考慮到實際工程中灌注樁與土體的摩擦及咬合作用，假定螺牙下底面完全粗糙，壓密區與螺牙下底部夾角為，螺旋線中心為點，同時假定計算由滑動區自重引起的承載力時螺旋中心線也是點

馬來西亞測繪局（JUPEM）為了推進馬來西亞空間數據基礎設施（MyGDI）建設，于2002年12月設立了馬來西亞地理空間數據基礎設施中心（MaCGDI），歸馬來西亞自然資源與環境部（NER）領導，取代了之前的土地信息系統國家基礎設施秘書處（NaLIS）。MaCGDI負責協調各級政府部門的地理空間信息存取與分發工作，確保能不間斷地存取和使用最新的、最精確的地理空間數據。

基礎醫學“整體功能”立體教學模式的實施是一項系統工程，它涉及到教學理念、教學管理、教學模式、教學內容以及教材等多方面的改革。以提高醫學生崗位勝任力為目標的“三導向”培養模式下，專業素質培養過程中構建了具有我院特色的基礎醫學整體整合課程體系，在實踐中我們將加強對教師和學生的全方位評價，隨著經驗的積累，我院的“整體功能”立體教學模式必將不斷地發展與完善，并將為兄弟院校的教學模式改革提供有益的指導和借鑒。

在社會工作專業教育的“非傳統”視角下，上述機構所需的人才培養完全是可以嵌套在已有的社會工作碩士項目的培養環節之中，而社會公益高端人才的培養也是屬于社會工作專業教育與培養范疇內應該關照的重點。遺憾的是，我國第一個旨在培養具備社會責任感、創新意識、管理能力和實踐能力，并致力投身于社會公益事業的高級管理人才或社會企業家的社會公益管理碩士項目(Master of Social Enterprise Management，簡稱MSEM)，卻是由上述的傳統意義上只關注于市場或企業領域經管人才培養的北京大學光華管理學院與中國銀泰投資有限公司、北京銀泰公益基金會發起和推行的。

(3)假定邊上豎向力均勻分布且僅考慮土體自重，即=

上述3個假定中，實際上面上的側摩阻力略大于tan，這里主要忽略了極限承載狀態下樁土界面間殘余黏結力，考慮到該值與側摩阻力相比較小，故而未計入此外，面上豎向應力取時忽略了土體之間抗剪強度提供的豎向應力，小于實際值，然而該面上的豎向應力分布形式及數值的選取一直未得到精確解答本文參考太沙基推導地基極限承載力時所作假設，假定面上的豎向壓力為均勻分布，其值取

2.2 螺牙極限承載力計算

根據太沙基研究成果，從實際工程要求的精度出發，計算基礎極限承載力時可將其分為3種原因引起的極限承載力的總和：① 土體無質量，有黏聚力和內摩擦角，無超載，即=0，≠0，≠0，=0；② 土體無質量，無黏聚力，有內摩擦角，有超載，即=0，=0，≠0，≠0；③ 土體有質量，無黏聚力，有內摩擦角，無超載，即≠0，=0，≠0，≠0本文將前兩種原因歸為一類進行計算.

美方語料在構建IDC元素時，大量應用指示“特朗普”的名詞詞組及輔助詞項“特朗普政府”“USTR”，突出特朗普及本屆政府推行的政策與往屆政府不同，宣稱其更符合美國人民利益，試圖增強特朗普的聲望，贏得選民支持。因而，“美國人民”“我們”都成為IDC的重要元素，努力構建特朗普親民的形象，通過人民的支持獲得其政策的合法性。復數名詞“農民們”“工人們”“消費者們”通過轉喻機制指代美國人民，但將其具體化的話語優勢在于引導民眾相信總統在給予人民真切的人文關懷。

(3)螺牙豎向應力.

(1)面上的應力.

對于螺旋過渡區(區域)，滑動面上土體正應力與切應力之間關系為=tan+，其中正應力與其產生的摩阻力tan的合力與滑面法向夾角為，即指向螺旋線的中心，如圖2所示圖中：為螺旋曲線的最大旋轉角；為螺旋曲線的旋轉半徑；、分別是面上的正應力、切應力；為面上的正應力；指數螺旋線的方程為

=etan

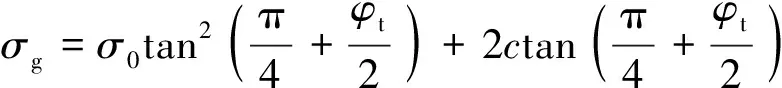
滑動面上取微段d對點求力矩，則d=dcos=d，其中為滑動面長度，為彎矩由點力矩之和為0可得(不計入滑動區重力)：

(3)

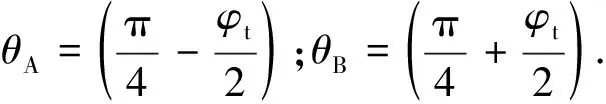
由式(3)解得：

=(cos+tansin)+

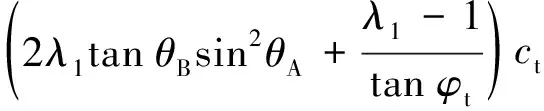
(4)

=tan+

(5)

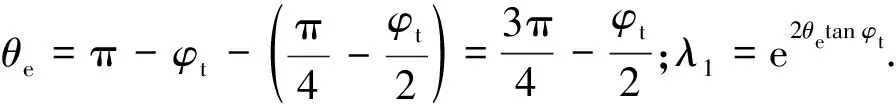
(2)面上應力.

對于彈性壓密區，假定螺牙達到極限承載力時，面上只有正應力，而無切應力，如圖3(a)所示.圖中：為螺牙底面與土體之間的法向應力；為表面與壓密核之間的法向應力.則由方向力系平衡關系可得：

∑=

sin+cos-cos=0

(6)

式中：∑為方向的合力.

解得：

(2)假定承載極限時面正應力為=，其中為靜止土壓力系數，為土體重度，為埋深；切應力=tan，為樁土界面摩擦角，取065，面上土體與螺牙分離，二者相互作用為0

=+tan

(7)

..由埋深、黏聚力、摩擦角產生的承載力

對螺牙受力分析，假定螺紋樁在達到極限承載力時，面與土體脫空，二者之間無相互作用，此時螺牙上受到的豎向力除之外，還包括，如圖3(b)所示.因此螺牙上平均豎向應力為

有涂層的原始樣品表面和截面的掃描電鏡圖如圖4所示.圖4(a)顯示，樣品表面有起伏不平的扁平凸起，沒有孔洞.圖4(b)顯示，涂層和碳鋼基底之間結合緊密，看不到縫隙，涂層內部干燥后沒有裂紋.將有涂層的樣品在500 ℃加熱8 h后，其表面和截面掃描電鏡圖如圖5所示.圖5(a)顯示，樣品表面基本上是平坦的，依然看不到孔洞.圖5(b)顯示，涂層和碳鋼基底之間結合緊密，看不到縫隙.

式中：為螺牙厚度；為螺牙高度；為與黏聚力相關的承載力系數；為與埋深相關的承載力系數.

哄的一聲，人群突然散開，把我擠在了前面，兩副擔架被人抬了出來。從身材的魁梧程度看，第一個抬出的應該是二狗子，只見那露出的胳膊，密密麻麻布滿了針眼。

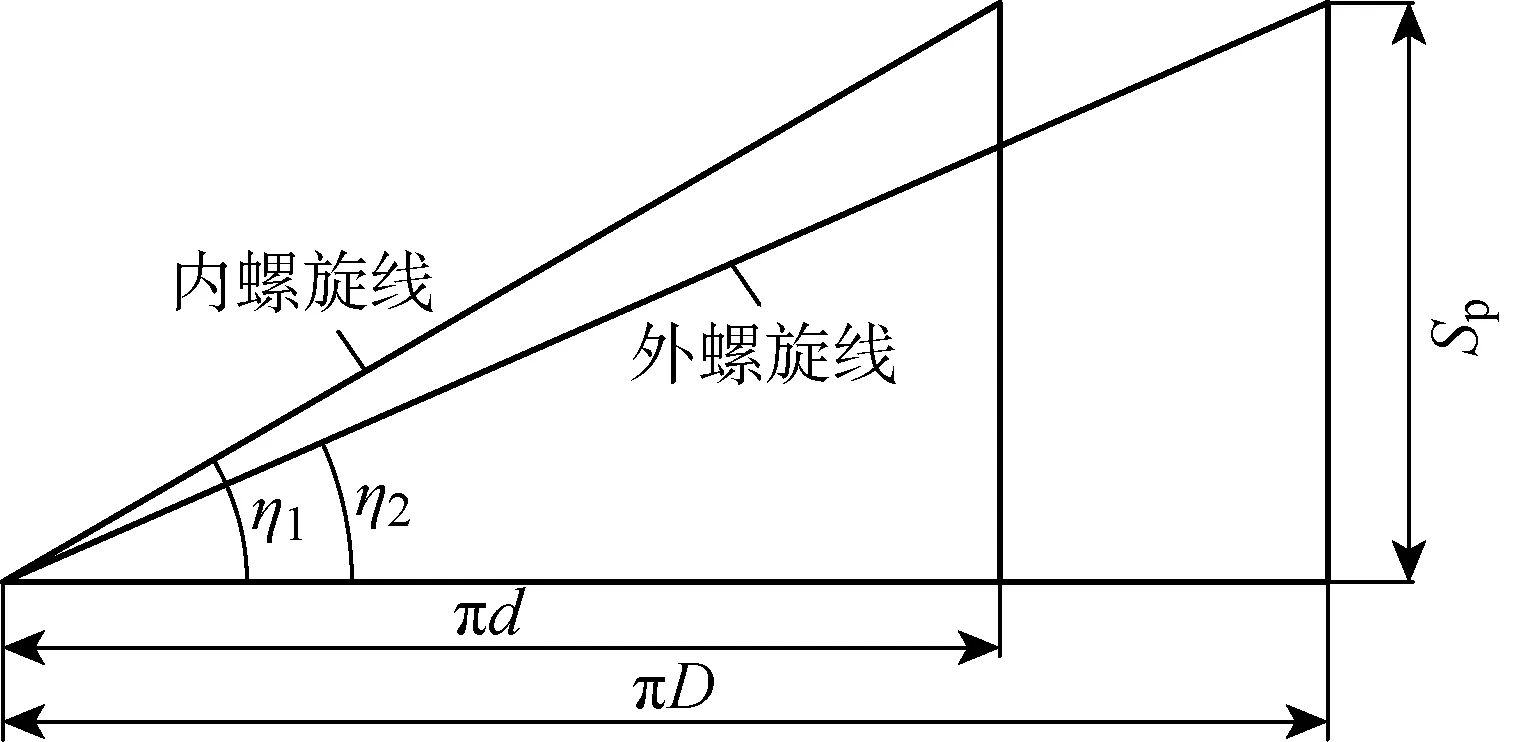
..螺距大于臨界螺距 若上下螺牙塑性區不相互影響，二者之間的距離必然要大于某一數值，將其命名為臨界螺距.根據Rao等的研究，若螺旋鋼樁(螺紋樁前身)達到極限承載力時產生圓柱形剪切破壞，/的值需小于3，考慮到螺旋鋼樁外徑一般為其內徑的數倍，因此/的值實際由葉片的螺距與懸臂端長度(對應于螺紋樁的螺牙高度)的比值來決定.因此，確定混凝土螺紋樁臨界螺距時，需對上述方法進行一定的修正.結合《螺紋樁技術規程》，本文建議當與的比值/<6時，計算螺紋樁極限承載力采用圓柱形剪切破壞模型；當螺距/>6且>時，采用單獨承載破壞模型，即此時>.

面上的側向壓力呈三角分布，切應力為0，則其合力作用于距離點3處，塊體受力如圖4所示而面上反力作用于距離點23處，并且與面法向夾角為，其方向為豎直向下.

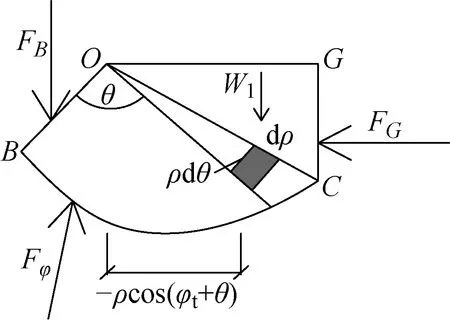
對于區域，面上反力正指向點，對點取矩為0同時，取面積微元d，該微元土體到點的水平距離為，假定微元位于點左側時為負，右側為正，則=-cos(+)，微元重力對點力矩為

d=d=-ddcos(+)

式中：為面積微元到點的距離由點力矩為0可得：

乍見此人，老太醫和喬十二郎都大吃一驚，此人竟是刑部趙大人。喬十二郎剛想喊一聲“趙伯伯”，趙大人卻不看他一眼，微笑著徑直走向老太醫。

(5)“有效氯含量”可用來衡量含氯消毒劑的消毒能力,其定義是:每克含氯消毒劑的氧化能力相當于多少克Cl2的氧化能力。NaClO2的有效氯含量為____。(計算結果保留兩位小數)

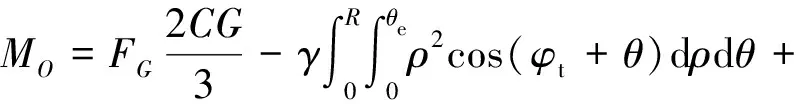
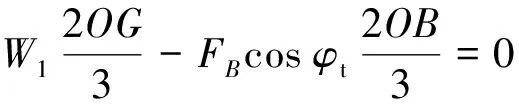
(9)

式中：為面上的合力；為土塊的自重.

解得:

譯文二：是不是他的太太有私房錢？瞎掰！弗林特小姐出身于白金漢郡的一個小地主家庭，兄弟姐妹連她共有十一個人。

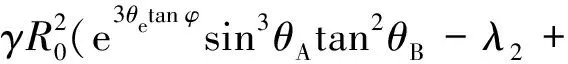
e3tan sincos)2cos

對于承臺受力，內力控制截面為XY截面Z向壓力，在左線隧道掘進后0#承臺變化量為0.14%，1#承臺變化量為1.1%；彎矩控制截面為YZ截面Y向彎矩，0#承臺變化量為-2.4%，1#承臺變化量為-7.6%，由此可見隧道掘進引起的承臺內力變化較小。

(10)

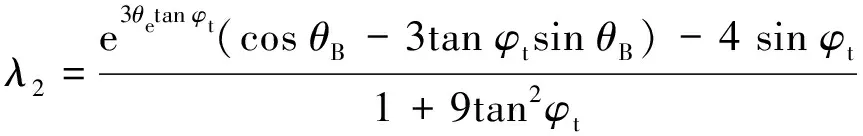
(2)塊受力.

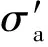
(11)

式中：為壓密核自重.

解得：

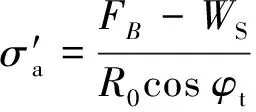
(12)

即由土體自重引起的螺牙上平均豎向應力為

式中：為與土體重度相關的承載力系數.

綜上，螺牙達到極限承載階段時所受的豎向壓力為

目前，GLP-1對β細胞的保護作用已經得到證實。其對β細胞的保護作用，主要是在促進β細胞增殖、誘導β細胞再生以及抑制β細胞消亡等方面發揮其作用。GLP-1對β細胞的保護作用機制尚未十分清楚，可能與以下幾個方面的因素有關：①GLP-1受體激活后主要通過T細胞核因子或β連鎖蛋白所依賴的Wnt信號系統，調節β細胞增殖和胰島素生成的關鍵因子，從而刺激β細胞的增殖，促進β細胞的生存；②在體外β細胞系，GLP-1受體的激活能夠保護β細胞細胞功能，免受各種損傷因素的影響。此外，有多種證據表明GLP-1可以誘導胰腺細胞、小腸表皮細胞以及胰腺中胰島來源的前體細胞分化成為β細胞或具有分泌胰島素功能的細胞[9]。

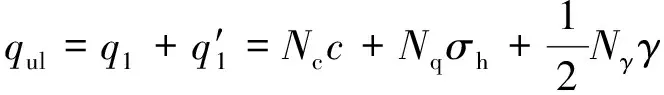
(14)

2.3 螺紋樁極限承載力計算

(1)塊受力.

當>時，螺紋樁承載力由螺牙承載力、樁芯側摩阻力、樁底承載力3部分組成.

(1)螺牙承載力.

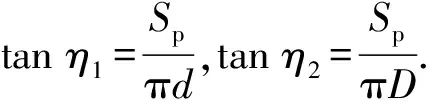
d高度內，螺牙豎向投影面積為

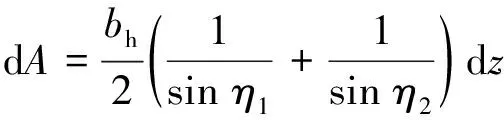
式中：為埋深.

式中：Bd —燃料消耗量（kg/h）；ey —空預器出口空氣 （kJ/kmol）；e0—空預器入口空氣（kJ/kmol）；—燃燒和脫硫當量理論空氣量（m3/kg）；eCO2—爐膛出口二氧化碳 （kJ/kmol）；—環境溫度下二氧化碳 （kJ/kmol）；—煙氣中二氧化碳體積（m3/kg）—煙氣中過量空氣體積（m3/kg）；ekl —爐膛出口空氣 （kJ/kmol）。

“在雪夜曬月亮，我們都快凍成四根凌冰掛樹上了，你們兩位就披一件葛布的袍子，不冷嗎？烏有先生你還搖著你的紙扇子，會傷風的啊！”上官星雨說。

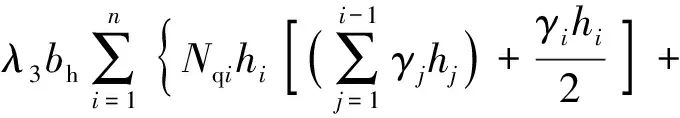
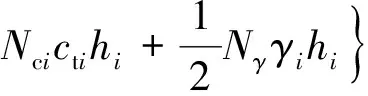
(15)

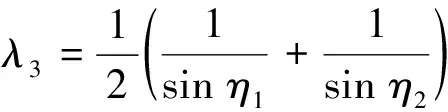
式中：、分別為土層編號；為第層土體厚度；為第層土體重度；q、c、γ為第層土體承載系數.

(2)樁芯側摩阻力.

螺牙下土體受力狀態復雜，壓密核附近的豎向承載力主要由螺牙提供，本文在計算樁芯側摩阻力時不計入壓密區的摩阻力，上下螺牙間有效樁芯摩擦高度為

=--

(16)

式中：為螺牙下側滑動邊界與點的最大豎向距離.

螺旋線邊界上任意一點與點的豎向距離為

=etan sin(+),+?(0，)

(17)

對求的導數，令其等于0，得：

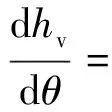
etan [cos(+)tansin(+)]=0

(18)

..由滑動區自重產生的極限承載力

因此：

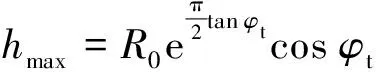
(19)

螺紋樁樁芯有效摩擦區展開后如圖7所示，圖中(=0,1,…,)為第層土體底部埋深，為螺牙旋轉周數取微元面積d，則d=ddtan，考慮到埋深遠大于，忽略土體高度引起的側摩阻力，故而微元面上的極限摩阻力為

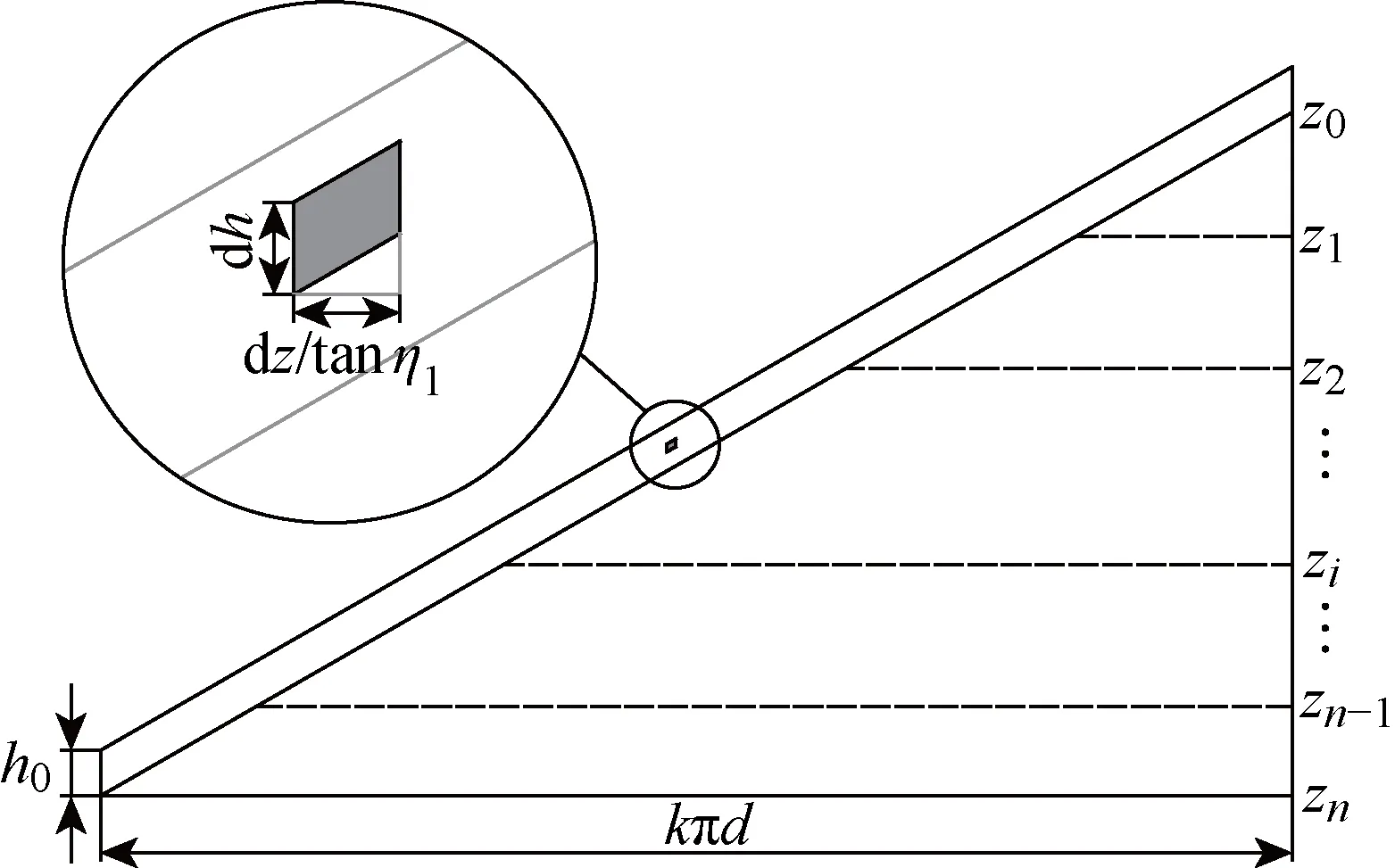
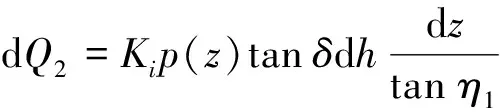
式中：為樁芯側摩阻力；為第層土體靜止土壓力系數；()為埋深處的土體自重應力.

樁芯極限側摩阻力為

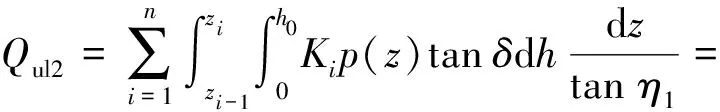
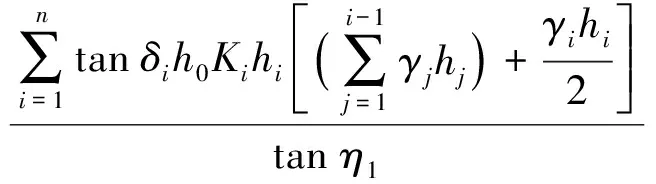
(20)

(3)樁端承載力.

計算樁端承載力時，樁端面積按樁芯底面積來計算，即=π/4，根據《建筑樁基技術規范》，極限端阻力標準值為

=

(21)

式中：為端阻力標準值.

綜上，螺距大于臨界螺距的螺紋樁極限承載力計算公式如下：

=++=

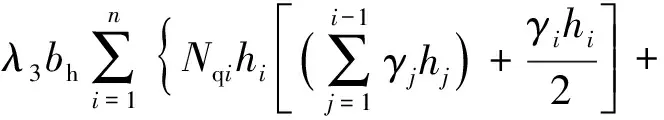
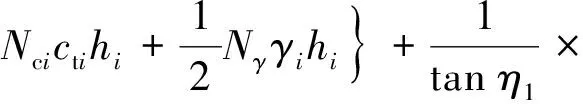
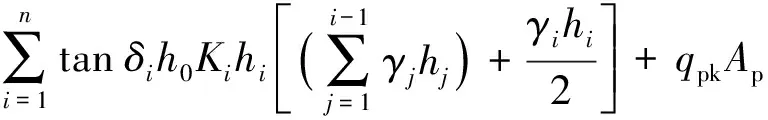
(22)

..螺距小于臨界螺距 當≤時，上下螺牙之間作用交叉明顯，太沙基極限平衡理論不再適用于螺紋樁極限承載力的計算.根據既有研究及《螺紋樁技術規程》，螺紋樁達到極限荷載時沿樁體外徑呈圓柱形剪切破壞，如圖8所示，圖中、分別為圓柱剪切面上不同位置的極限切應力.此時螺紋樁的極限承載力計算方法如下：

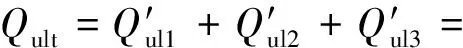
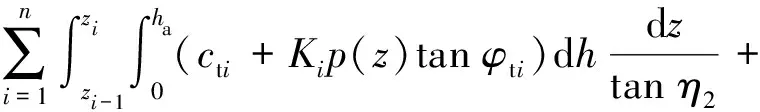
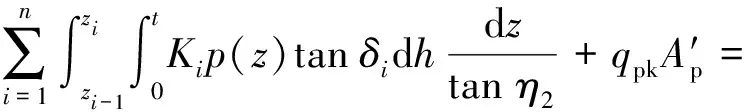
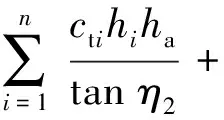
(23)

3 實例驗證及參數討論

某工地現場試驗的樁型中，灌注螺紋樁的內徑為400 mm、外徑為560 mm、螺齒寬為80 mm、螺距為700 mm、樁長為8 m、寬厚比為1，干作業鉆孔樁.現場試驗場地工程地質條件如表1所示，所在土層為粉質黏土，土體重度平均為19 kN/m.

螺紋樁參數/>6且>，采用式(22)對螺紋樁承載力進行計算，螺紋樁極限端阻力標準值根據《建筑樁基技術規范》取 1 000 kPa.當取0時(即按M-C屈服準則計算)，螺紋樁承載力計算結果如表2所示.

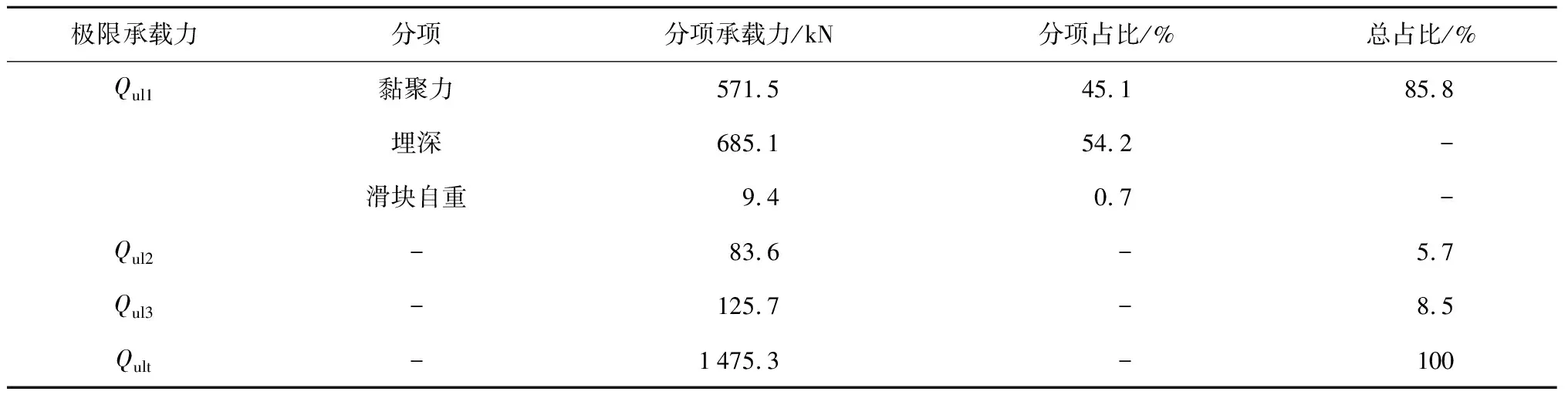
可以發現，螺紋樁極限承載力理論值為 1 475.3 kN，螺牙提供的承載力達到了螺紋樁極限承載力的85%左右，而同外徑混凝土圓樁極限承載力約為 1 100 kN，側摩阻力占總承載力的77%.可以看出，螺牙的存在不但改變了樁體的承載特性，而且大大提高了承載力.同時發現，螺牙提供的極限承載力主要由土體、及樁體埋深決定，而滑塊自重(非土體自重)引起的承載力僅占螺牙承載力的1%左右，因此忽略滑塊自重對滑動面的影響，假定對數螺旋線的中點為點是合理的.

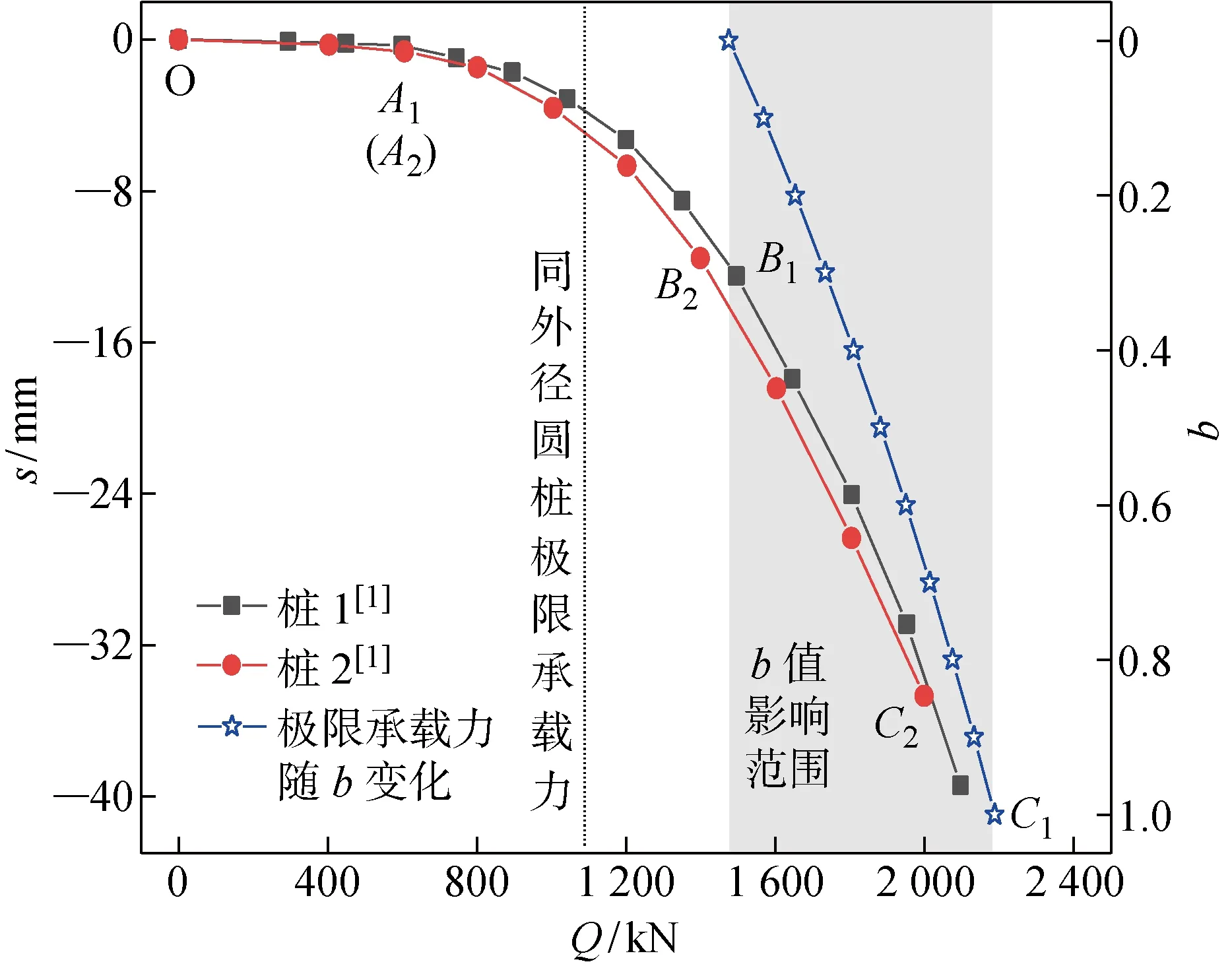
圖9所示為螺紋樁承載力現場實測與理論值對比圖，圖中為樁所受荷載，為樁體沉降可以發現，螺紋樁沉降曲線可以分為3個階段：直線增加段(包括與，下同)、過渡段及迅速沉降段，本文推導的極限承載力下限值正好位于過渡段與迅速沉降段的過渡點點附近.根據《建筑基樁檢測技術規范》規定，對于緩變型-曲線，取沉降值達到40 mm時對應的荷載為極限承載力，對于陡降型-曲線，取拐點處荷載為極限承載力.本文中螺紋樁-曲線屬于二者之間的過渡型，在判定極限承載力時徐春華等選擇沉降40 mm時的荷載為極限承載力，分別為 2 000 kN及 2 100 kN，但是考慮到過渡點以后樁沉降速率明顯過大，對工程的安全性極為不利.因此，本文認為選取點或者點與40 mm之間的某個點對應的荷載為極限承載力更為合適，即螺紋樁極限承載力在 1 500～2 000 kN之間.從圖9中可以看出，當從0增大到1時，本文方法推導的螺紋樁極限承載力從 1 475 kN增加到了 2 187 kN，增幅約48%，說明極限承載力隨著的增大而顯著提高，計算過程中考慮該值的影響能更好發揮土體的承載潛能.當值取值合適時，本文方法計算結果與螺紋樁實際極限承載力將更加接近.

從前文推導中可以發現，除樁徑等常規參數外，影響螺紋樁承載力的主要參數包括、及.圖10所示為螺紋樁在=0時滿足單獨承載破壞條件下極限承載力隨其關鍵參數的變化曲線，圖中為參數尺寸.可以發現，對螺紋樁承載力影響最為明顯，當從0.06 m增加到0.15 m時，螺紋樁承載力隨之增加了約2倍，從 1 129 kN增加到了 3 096 kN，即較小螺牙高度的增加即可帶來明顯的承載力提升.然而，考慮到當螺牙高度較大時，螺牙懸臂端過長，容易產生沖剪破壞，而且螺牙下土體塑性區的發展受到限制，當螺牙高度超過到某一數值時，反而可能造成螺紋樁承載能力下降，這也是設計人員在螺紋樁設計過程中需注意的問題.

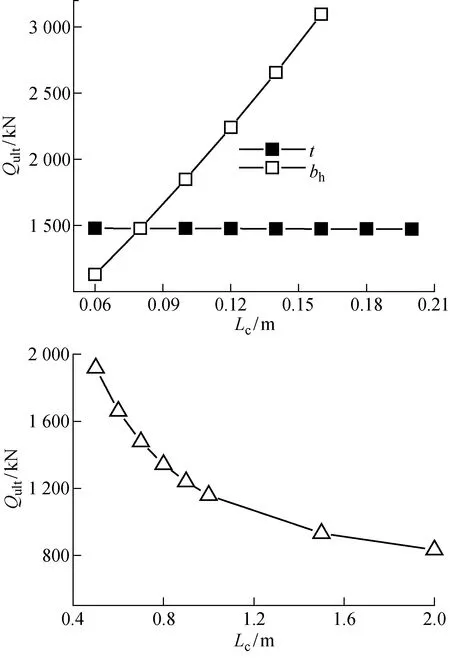
同時可以看出，螺牙厚度對螺紋樁承載力幾乎沒有明顯影響，這是因為螺紋樁的承載力主要由螺牙下土體提供，而螺牙側面面積較小，提供的承載力有限，故在螺紋樁設計過程中，在滿足螺牙抗剪強度的前提下，可適當減小螺牙厚度，為螺牙間土體提供更多的塑性變形空間.當螺牙滿足單獨承載破壞條件時，隨著螺距的增加，螺紋樁承載力先迅速降低.這是因為當螺距增加的時候，與螺旋線傾角相關的系數非線性降低，進而使得螺牙受力總面積迅速減小，極限承載力銳減.之后當螺距增加到一定范圍時，承載力下降趨于平緩，這時螺牙提供的承載力僅占樁體的總承載力的一小部分，螺紋樁朝著混凝土圓樁的方向“退化”.因此，在保證螺牙下土體塑性區能充分發展的前提下，若要提高螺紋樁承載力，可適當減小螺距，使得螺牙下土體盡可能多的產生塑性破壞.

4 結論

針對螺紋樁承載機理不清、既有極限承載力計算不準確等問題，基于統一強度理論與太沙基極限平衡理論，推導了螺紋樁極限承載力計算公式，提出了螺紋樁不同模式下臨界螺距的確定方法和極限承載力計算方法，并討論了螺紋樁各參數對其承載力的影響，得出以下結論：

(1)螺紋樁極限樁承載力是同外徑圓樁的 1.5～2倍，螺牙提供的承載力主要由土體黏聚力、內摩擦角及埋深決定，滑塊自重貢獻的承載力相對較小.

(2)統一強度理論參數從0增加到1時，螺紋樁極限承載力理論值約增大48%，取值合適時可以更準確地預測螺紋樁實際承載力，具有較好經濟性、合理性.

(3)螺紋樁關鍵參數中，螺牙高度對其極限承載力影響最大，二者基本呈線性相關，而螺牙厚度對承載力基本不產生影響.

(4)在保證螺牙抗剪滿足要求時，可適當增加螺牙高度，減小螺距，使得螺紋樁樁側土體最大限度進入塑性變形，以提高螺紋樁極限承載力.