代數正矩陣的若干研究
田 巖, 焦 旸
(遼寧師范大學 數學學院,遼寧 大連 116029)
符號模式矩陣主要通過實矩陣的元素符號來研究矩陣具有的僅與其元素的符號有關而與元素的數量大小無關的組合性質.矩陣的每個元素都是正數的實矩陣稱為正矩陣.2016年, Steve Kirkland、Pu Qiao和Xingzhi Zhan[1]引入了代數正矩陣的概念:對于實矩陣A,如果存在實多項式f使得f(A)是一個正矩陣,那么A稱為代數正矩陣.他們提出符號模式矩陣要求代數正和允許代數正這兩個問題.2019年,Sunil Das和Sriparna Bandopadhyay[2]給出了代數正矩陣新的刻畫,并且研究樹符號模式矩陣允許代數正和要求代數正.本文將研究代數正矩陣的一些性質,給出代數正矩陣的性質在研究3階不可約的三對角符號模式矩陣是允許代數正問題中的具體應用.
符號模式矩陣(簡稱符號模式)是指所有元素都來自集合{+,-,0}的矩陣.任意實矩陣A=(aij),以aij的符號為元素構成的符號模式矩陣稱為A的符號模式矩陣.與符號模式矩陣A符號相同的矩陣構成的實矩陣集合用Q(A)表示.設符號模式矩陣A有性質P,如果Q(A)中每一個矩陣都具有性質P,則稱符號模式矩陣A要求P.設符號模式矩陣A具有性質P,如果Q(A)中存在一個矩陣具有性質P,則稱符號模式矩陣A允許P.
一個正矩陣(非負矩陣)是指所有元素都是正(非負)實數的矩陣.若矩陣A是正矩陣,即矩陣中每個元素都大于0,記作A>0.diag(d1,d2,…,dn)表示對角線元素為d1,d2,…,dn的對角矩陣.f(A)表示將矩陣A代入多項式f(x).矩陣A的第i行j列元素用A(i,j)表示.本文研究的矩陣都是實方陣.
1 代數正矩陣的性質
定義2.1[1]設A是實方陣,如果存在一個實系數多項式f,使得f(A)是一個正矩陣,則稱A是代數正矩陣.
定義2.2設A是符號模式矩陣,若任意實矩陣B∈Q(A)都是代數正的,則稱符號模式矩陣A是要求代數正的.
定義2.3設A是符號模式矩陣,若存在實矩陣B∈Q(A)是代數正的,則稱符號模式矩陣A是允許代數正的.
引理2.1設A是n階實矩陣,A是代數正矩陣當且僅當存在一個次數≤n-1的實系數多項式f(x),使得f(A)>0.
證因為A是代數正的,根據定義2.1,設存在一個實系數多項式g(x),使得g(A)>0.設A的特征多項式為
f(λ)=λn+an-1λn-1+…+a1λ+a0.
由Cayley-Hamilton[3]定理可知,
f(A)=An+an-1An-1+…+a1A+a0I=0.
由于
g(x)=f(x)h(x)+r(x),
其中,h(x)和r(x)為實系數多項式, ?(r(x))
由于
g(A)=f(A)h(A)+r(A),
則
g(A)=r(A),
故?(g(A)) 例1證明n階上三角矩陣(或下三角矩陣)一定不是代數正的. 證假設n階上三角矩陣A是代數正的, 根據引理2.1, 存在一個次數≤n-1的實系數多項式 f(x)=an-1xn-1+an-2xn-2+…+a0(ai∈,i=0,1,…,n-1), 使得 f(A)=an-1An-1+an-2An-2+…+a1A+a0I>0. 顯然,Am(m=1,2,…,n-1)是上三角矩陣, 所以f(A)是上三角矩陣, 故不是正矩陣, 這與f(A)>0矛盾.因此,n階上三角矩陣A不是代數正的. 同理可證,下三角矩陣不是代數正的. 引理2.2矩陣A是代數正矩陣當且僅當PAPT是代數正矩陣, 其中,P為置換矩陣. 證因為A是代數正矩陣, 根據引理2.1, 存在一個次數≤n-1的實系數多項式 f(x)=an-1xn-1+an-2xn-2+…+a0(ai∈,i=0,1,…,n-1), 使得f(A)>0,即 f(A)=an-1An-1+an-2An-2+…+a0I>0. 設P為置換矩陣, 則Pf(A)PT>0, 即 Pf(A)PT=P(an-1An-1+an-2An-2+…+a0I)PT =an-1PAn-1PT+an-2PAn-2PT+…+a0IPPT =an-1(PAPTPAPT…PAPT)+an-2(PAPTPAPT…PAPT)+…+a0I =an-1(PAPT)n-1+an-2(PAPT)n-2+…+a0I =f(PAPT), 故f(PAPT)>0, 所以PAPT是代數正的. 反之, 設PAPT是代數正的, 則存在實系數多項式f(x), 使得f(PAPT)>0.顯然PT是置換矩陣, 則f(A)=f(PT(PAPT)P)=PTf(PAPT)P>0, 故A是代數正的. 推論2.3設A是n階實矩陣, 若A是代數正矩陣當且僅當DAD-1是代數正矩陣, 其中,D為對角矩陣, 并且對角線的所有元素符號相同. 證因為A是代數正的, 根據引理2.1, 設存在一個次數≤n-1的實系數多項式 f(x)=an-1xn-1+an-2xn-2+…+a0(ai∈,i=0,1,…,n-1), 使得f(A)>0, 即f(A)=an-1An-1+an-2An-2+…+a0I>0. 設D=diag(d1,…,dn),di(i=1,…,n)符號相同, 故Df(A)D-1>0,即 Df(A)D-1=D(an-1An-1+an-2An-2+…+a0I)D-1 =an-1DAn-1D-1+an-2DAn-2D-1+…+a0DID-1 =an-1(DAD-1)n-1+an-2(DAD-1)n-2+…+a0I, =f(DAD-1), 所以f(DAD-1)>0, 因此DAD-1為代數正的. 反之, 設DAD-1是代數正的, 那么存在實系數多項式f(x), 使得f(DAD-1)>0.顯然,D-1是置換矩陣, 則 f(A)=f(D-1(DAD-1)D)=D-1f(DAD-1)D>0, 故A是代數正的. 注對于任意的可逆矩陣Q,QAQ-1不一定能夠保持代數正的性質. 例2考慮n階實對稱的代數正矩陣 根據引理2.1, 存在一個次數≤n-1的實系數多項式 f(x)=an-1xn-1+an-2xn-2+…+a0(ai∈,i=0,1,…,n-1), 使得f(A)>0, 即f(A)=an-1An-1+an-2An-2+…+a0I>0.由于A是對稱矩陣, 則存在可逆矩陣Q, 使得QAQ-1=diag(λ1,λ2,…,λn), 其中,λi(i=1,2,…,n)是A的特征值, 顯然f(QAQ-1)不是正矩陣, 所以QAQ-1不是代數正的. 將文獻[4]的定理3進行推廣,得到下列代數正矩陣的充分必要條件. 引理2.4設A是n階實矩陣,A是代數正的當且僅當下列條件之一成立: 1)AT是代數正的; 2)-A是代數正的; 3)βA+αI是代數正的, 其中,α∈,β∈{0}. 證1)必要性.因為A是代數正的, 所以根據引理2.1, 設存在一個次數≤n-1的實系數多項式 f(x)=an-1xn-1+an-2xn-2+…+a0(ai∈,i=0,1,…,n-1), 使得f(A)>0, 故f(A)T>0, 即 f(A)T=(an-1An-1+an-2An-2+…+a0I)T =an-1(An-1)T+an-2(An-2)T+…+a0IT =an-1(AT)n-1+an-2(AT)n-2+…+a0I =f(AT)>0, 所以AT為代數正矩陣. 充分性.設AT是代數正的, 則根據引理2.1, 存在一個次數≤n-1的實系數多項式 g(x)=bn-1xn-1+bn-2xn-2+…+b0(bi∈,i=0,1,…,n-1), 使得g(AT)>0, 所以(g(AT))T>0, 即 (g(AT))T=bn-1((AT)n-1)T+bn-2((AT)n-2)T+…+b0I =bn-1((AT)T)n-1+bn-2((AT)T)n-2+…+b0I =bn-1An-1+bn-2An-2+…+b0I>0, 故(g(AT))T=g(A)>0, 所以A為代數正矩陣. 3)必要性.設A是代數正的, 根據引理2.1, 則存在實系數多項式f(x), 使得f(A)>0.設q(x)為實系數多項式, 使得 則 q(βA+αI)=f(A)>0, 所以βA+αI是代數正的. 當β=-1,α=0時,A是代數正的當且僅當-A也是代數正的, 所以2)成立. 引理2.5設A是n階實矩陣, 若A是代數正矩陣當且僅當(DP)A(DP)-1是代數正矩陣, 其中,D是對角矩陣,并且對角線的所有元素符號都相同,P是置換矩陣. 證因為A是代數正的, 根據引理2.1, 存在一個次數≤n-1的實系數多項式 f(x)=an-1xn-1+an-2xn-2+…+a0(ai∈,i=0,1,…,n-1), 使得f(A)>0, 即f(A)=an-1An-1+an-2An-2+…+a0I>0. 設D=diag(d1,d2,…,dn),di(i=1,2,…,n)符號相同, 則(DP)f(A)(DP)-1>0. (DP)f(A)(DP)-1=(DP)(an-1An-1+an-2An-2+…+a0I)(DP)-1 =an-1(DP)An-1(DP)-1+an-2(DP)An-2(DP)-1+…+a0(DP)I(DP)-1, =an-1(DPAP-1D-1)n-1+an-2(DPAP-1D-1)n-2+…+a0I =f(DPAP-1D-1), 所以f(DPAP-1D-1)>0,故(DP)A(DP)-1是代數正的. 反之, 假設(DP)A(DP)-1是代數正的, 則存在實系數多項式f(x), 使得f((DP)A(DP)-1)>0.那么 f(A)=f((DP)-1((DP)A(DP)-1)(DP))=(DP)-1f(DAD-1)(DP)>0, 故A是代數正矩陣. 下面將所有3階不可約三對角符號模式矩陣進行分類,給出3階不可約三對角符號模式矩陣是允許代數正的充分必要條件, 從而給出代數正矩陣性質的具體應用. 設V是有限集合,E?V2, 則集合對D=(V,E)稱為一個有向圖.n階實矩陣A=(aij)的有向圖為D(A)=(V,E), 其中,V={1,2,…,n},(i,j)∈E當且僅當aij≠0. 定理3.1設A是3階不可約三對角符號模式矩陣,A是允許代數正的當且僅當A或-A置換相似于集合S中的矩陣: 其中,*∈{+,-,0}. 證必要性. (1)設A是3階不對稱的不可約的三對角符號模式矩陣, 則A或-A的形式如下: 易知, 無論A取上述何種形式,BA的圖都不是強連通的, 所以由參考文獻[5]定理3.2.1可知,BA是可約的.根據已知A是不可約的, 所以由文獻[4]定理4可知,A不是允許代數正的. (2)設A是3階對稱不可約三對角符號模式, 則A或-A置換相似于如下形式: 根據文獻[1]定理12易知,第一個符號模式矩陣滿足條件. 由于 充分性. 若A或-A置換相似于集合S中的第一個符號模式矩陣, 則Q(A)中存在矩陣M,M中除對角線以外的所有元素都非負.由文獻[1]定理5可知,M是代數正的, 因此, 集合S中的第一個符號模式矩陣是允許代數正的. 本文主要研究代數正矩陣的性質, 通過具體例題給出其應用.符號模式矩陣允許代數正和要求代數正是兩個著名公開問題,利用代數正矩陣的性質,將實矩陣進行約化,從而對于這兩個問題的研究提供了途徑和方法,具有一定的借鑒意義.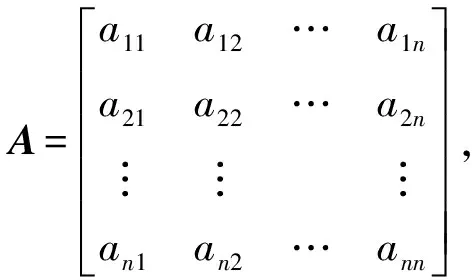

3 性質的應用


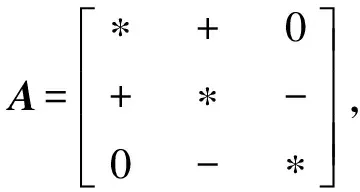
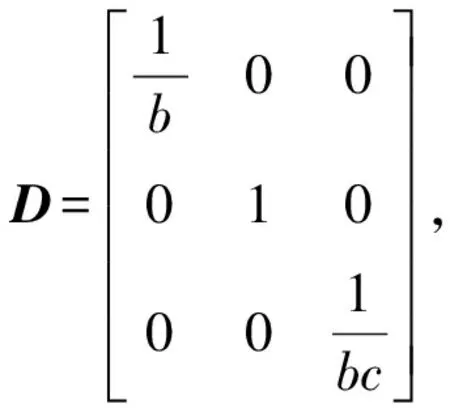
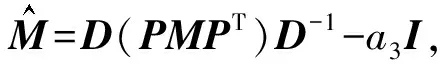


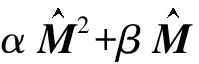

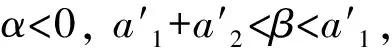



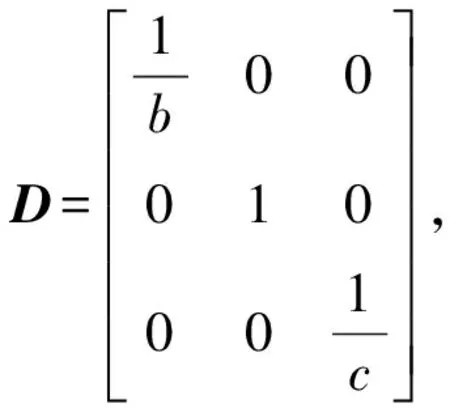

4 結 論

