潛水位氣壓效應的消除及消除效果評價

史昊鑫, 郭 健, 曲晨豪, 葛建宏

(成都理工大學 地質災害防治與地質環境保護國家重點實驗室, 四川 成都 610059)

地下水位一方面在某種程度上反映了巖石巖層的應力應變狀態,另一方面反映了地下含水層中水量的變化,因此,地下水位的計量常常是研究地下結構構造和地下水流動模式的基礎[1].潛水位受氣壓效應的影響較大[2],如果不能有效地消除氣壓效應的影響去正確計量水位,將有可能錯誤判斷巖石巖層的應力應變狀態,在地下水位比較平緩的廣闊平原區,還容易錯誤判斷區域地下水水力梯度的大小和方向[3].另外,在專門的水文地質試驗中,要精確獲取關鍵水文地質參數,往往也需要精準地監測地下水位數據[4].

國內外學者采用不同地區的水位和氣壓觀測資料對水位的氣壓效應進行了研究.Bredehoeft[5]最早開始研究各種要素對井水位變化的影響,并利用濾波方法和線性回歸方法來消除降雨和氣壓對井水位變化的影響;Roeloffs[6]通過分析承壓含水層的氣壓效應,運用最小二乘法線性回歸消除了氣壓對水位的影響;而Rojstaczer[7]通過研究指出,氣壓對水位的影響與氣壓的頻率有關;Matsumoto等[8]利用狀態空間模型并結合濾波方法,消除了固體潮、氣壓、降雨對井水位的影響.Toll等[9]提出使用BETCO軟件程序消除氣壓和固體潮對水位的干擾,這為地下水觀測數據的處理開辟了廣闊的前景;晏銳等[10]運用小波分析法將氣壓數據分解為不同頻段的時間序列,用最小二乘法求出氣壓響應系數,消除了氣壓對水位的影響;朱常坤等[11]利用連續小波變換對潛水位、氣壓進行多時間尺度分析,運用連續小波逆變換重構了氣壓和水位時間序列,然后用最小二乘法求出了氣壓效率,消除了氣壓對水位的影響.

以往對氣壓效應的研究主要集中在深層承壓含水層中,而在非承壓的潛水含水層中,少有氣壓效應影響消除的研究.為此,本文依據四川省中江縣垮梁子鄉一地下水監測系統中得到的高精度、高頻率特征數據,首先用斜率法和Clark法兩種方法求取氣壓效率,再通過線性回歸法和反卷積法得到消除氣壓效應后的校正水位,最后利用頻譜分析法來評價校正效果,旨在找到消除潛水含水層井水位氣壓效應的最佳方法.

1 數據來源與理論方法

1.1 數據來源監測井位于四川省中江縣垮梁子鄉的小山丘上,位置坐標為30°38′56″N、104°53′53″E.井口高程為528 m,水位埋深在21 m左右.井的水位監測設備為Micron’s Model MP102通氣式傳感器.地下水位數據的采集時間間隔設置為1 h,水位數據精度為1 mm,選取2018年8月25日至2019日2月18日時間段內共計3 216個井水位監測數據進行研究,得到井水位的變化曲線如圖1所示.

圖1 監測井水位變化曲線

同時選取Baro-Diver氣壓計,對研究區內大氣壓強進行實時監測,氣壓數據采集的時間間隔設置為1 h,精度約等于0.98 Pa.選取與水位監測數據相同時間段(2018年8月25日至2019年2月18日)的氣壓值并繪制曲線如圖2.

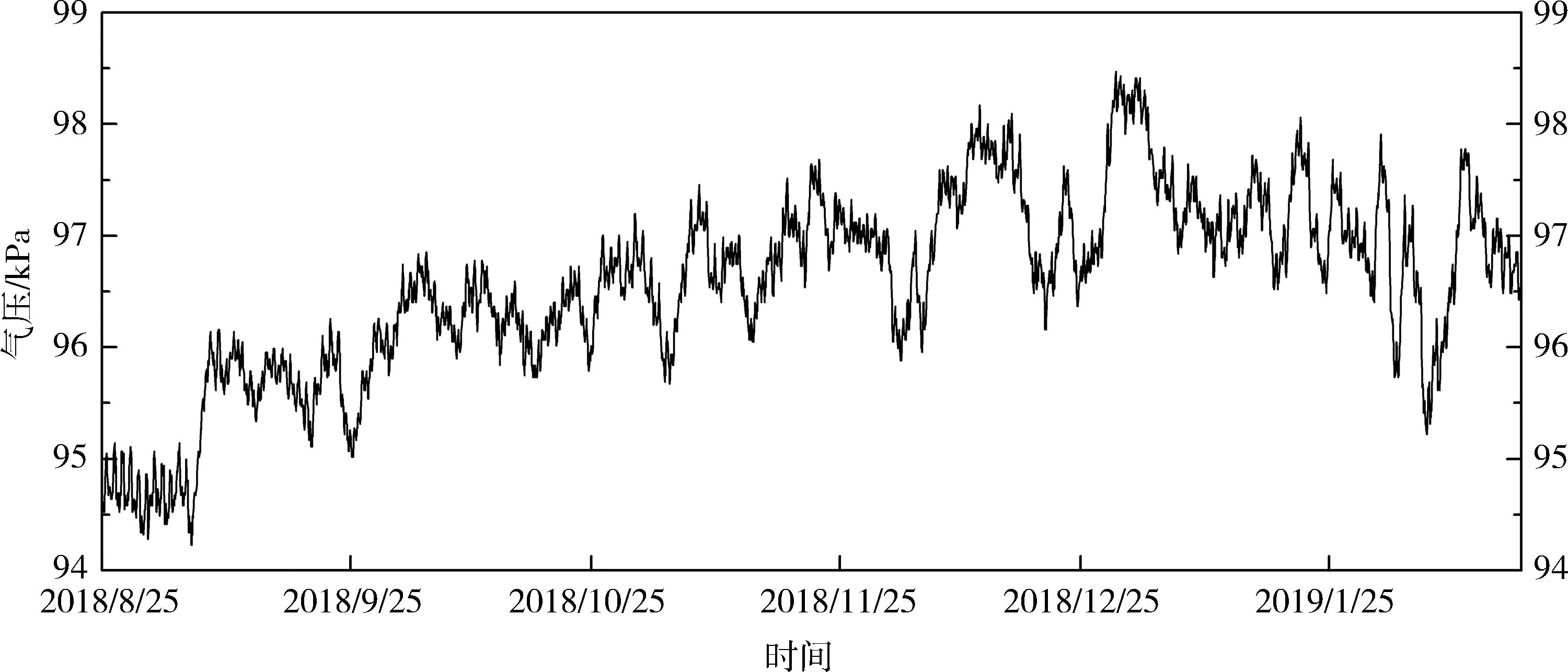
圖2 氣壓值變化曲線圖

該時間段的氣壓整體呈現上升趨勢.氣壓每小時變化最大值為411.879 3 Pa,小時變化的平均值為58.839 9 Pa;整個時間段的周變化量的最大值超過了1 961.33 Pa.

1.2 氣壓效應的響應原理潛水含水層的井水位受氣壓變化的影響,原因是大氣壓的變化傳遞到潛水面之前,空氣必須進入或離開上覆包氣帶.這個過程會受到非飽和帶的滲透性大小及其儲存或釋放土壤氣體能力大小限制,從而導致傳遞壓力過程變緩.因此,非飽和帶土壤里氣體壓強的變化會滯后于地面上的氣壓變化.這個滯后時間取決于含水層的性質(氣體滲透率、儲存率)以及現有的井況(井筒儲存和井壁薄壁效應).總之,造成滯后的關鍵因素是空氣通過包氣帶的氣動擴散系數和包氣帶的厚度[12].

然而,井中水位對氣壓變化的響應是瞬時的,導致井水和鄰近含水層中的水之間的壓力不平衡,這種壓力差使得井中水位發生波動.這個現象可以理解為作用到井水的氣壓要大于作用在潛水面的氣壓,如圖3.

圖3 潛水含水層氣壓效應示意圖

地面上大氣壓壓強變化了ΔB0不久后,只有其中的一部分ΔBt通過包氣帶傳到了潛水面,然而直接作用到井水面的壓強并未減小.因此,井水和含水層中的水之間會產生暫時的壓力不平衡,導致井水位下降,水位的值ΔWL等于ΔB0-ΔBt.最后,整個大氣壓強的變化會通過包氣帶逐漸作用到潛水面,即差值ΔWL會隨著時間逐漸消失,井水位慢慢恢復到與潛水面水位相同的位置[13].

1.3 氣壓效率的確定方法氣壓效率(Barometric Efficiency)的定義[9]可以由一個等式表示：

(1)

其中,ΔWb表示由于氣壓變化ΔB引起的那部分水位變化值,α為氣壓效率,無量綱.

氣壓效率表征了井水位變化對氣壓變化響應的敏感程度,其值為負,數值大小介于-1～0之間,確定氣壓效率的方法有斜率法和Clark法等.

1.3.1斜率法 斜率法是由Ferris等[14]基于多個時間間隔中的ΔW和ΔB比值提出.Y軸表示井水位的變化值ΔW,X軸表示大氣壓強的變化值ΔB.首先在坐標圖上點繪出ΔW和ΔB,用最小二乘法求取最佳擬合線,擬合線的斜率為氣壓效率的估值,則氣壓效率

(2)

其中

S

(3)

S

(4)

該方法存在的誤差,就是用ΔW代替了ΔWi,即忽略了其他因素(除氣壓以外)對水位變化造成的影響,誤差

εslope

(5)

其中

S

計算氣壓效率的誤差就是i時刻的非氣壓引起的水位變幅ΔWi與氣壓變幅ΔB之間的斜率,隨著采樣點的規模越大,產生這種誤差的可能性就越小.

1.3.2Clark方法 Clark方法是假設ΔWi不變,即假設井水位變化對除氣壓以外的影響因素來說是恒定的,計算氣壓效率的方法,要求水位數據采樣時間間隔的長度是恒定的[15].

該方法比較每個時間間隔上ΔW和ΔB的正負號,并計算

∑ΔWj=∑ΔWj-1+ωj,

(7)

其中,∑ΔWj表示第j個時間間隔后水位變化的和,∑ΔWj-1表示第j-1個時間間隔后水位變化的和,ωj表示如果第j個時間段內,氣壓變化Bj的符號和水位變化Wj的符號相同(即在某個特殊的情況下,當氣壓升高時,水位值也在升高;當氣壓下降時,水位值也在下降),則ωj的值就取水位變化值Wj的絕對值;如果兩者的符號相反,ωj的值將取水位變化值Wj的絕對值的負值.

如果Bj=0,則忽略Wj,這樣就避免了非氣壓效應引起的水位變化疊加,減小了計算誤差.

計算氣壓變化的原則是每個時間間隔的氣壓變化值的絕對值都會加到前一個時間間隔上去：

∑ΔBj=∑ΔBj-1+|ΔBj|,

(8)

那么氣壓效率的值就可以表示為

(9)

1.4 氣壓效應的消除方法

1.4.1線性回歸法 通過井水位數據與氣壓數據的相關性分析,通過最小二乘法得到回歸方程：Y=aX+b,Y表示水位埋深(m);X表示氣壓;a、b均為常數,其中a為氣壓效率α[16].

應用下式消除井水位中的氣壓影響成分,得到校正水位

(10)

1.4.2反卷積回歸法 在考慮氣壓效應滯后性的情況下,Rasmussen等[3]采用反卷積回歸法,利用水位-氣壓觀測值來估計氣壓響應函數,并通過響應函數計算修正水頭.該方法因為體現了氣壓效應的瞬時性特征,計算結果有較好的穩定性[17],故優于用一個氣壓效應常數去除氣壓擾動的效果.

Box等[18]建立了一套線性方程組估計氣壓響應函數

ΔW(t)=α(0)ΔB(t)+

α(1)ΔB(t-1)+α(2)ΔB(t-2)+…+

α(m)ΔB(t-m),

(11)

即

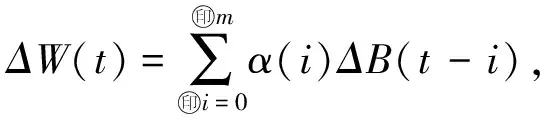
(12)

其中,ΔW(t)、ΔB(t)表示t時刻水位和氣壓的變化值,ΔB(t-i)表示t-1時刻氣壓的變化值,α(i)表示滯后i時的單位響應系數,m表示最大滯后時間.

對于瞬時響應,(11)式中只需保留第一項,其余全為0.通常來說,由于儲層效應、井壁效應、含水層覆蓋層效應以及氣壓變化與觀測水位響應之間的延遲等原因,氣壓響應函數存在多個滯后項.應將滯后的最大值設置為足夠大的數字,以便包括所有滯后響應.利用最小二乘線性回歸求出單位響應系數α.一旦找到α(j)的值,則通過對單位響應系數求和計算階躍式氣壓響應系數

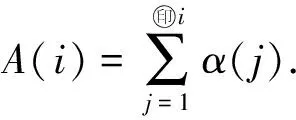
(13)

階躍氣壓響應函數用于判斷含水層類型(承壓或非承壓),如圖4[9].

圖4 承壓和非承壓含水層的階躍響應函數

利用響應函數,計算每個觀測值的修正值[9]：

2 氣壓效應消除結果

2.1 氣壓效率求取根據線性回歸法原理,氣壓效率是線性回歸法消除氣壓效應的重要參數.因此分別用斜率法和Clark法對氣壓效率進行求取,結果見表1.

表 1 井水位氣壓效率計算

根據結果可見,兩種方法確定的氣壓效率存在差異,Clark法得到的氣壓效率約為斜率法的1.7倍,哪個參數更準確?需要通過氣壓效應的消除效果來判斷.

2.2 氣壓效應消除

2.2.1線性回歸法消除 將斜率法獲得的氣壓效率α1=-0.199 0和Clark法獲得的氣壓效率α2=-0.346 4分別代入線性回歸(10)式對井水位數據進行校正計算.由于氣壓變化幅度以及氣壓效率值都比較小,使得在長時域內校正前后的水位變化不明顯,因此,選取某一周的原始水位與校正后的水位進行對比(圖5),由圖5可以看出,采用斜率法得到的氣壓效率消除氣壓效應的效果不明顯,用Clark法得到的氣壓效率進行氣壓效應消除后,水位有明顯的校正.

圖5 線性回歸法消除氣壓效應前后水位對比圖

2.2.2反卷積回歸法消除 將滯后時間的最大值m設為24 h,通過多元線性回歸,求得每個水位變化ΔW(t)與不同滯后時間的氣壓變化ΔB(t-i)之間的線性關系,得到每個滯后時間i的ΔB前的單位響應系數值.

再根據(13)式,得到兩個監測端水位滯后時間1～24 h的階躍氣壓響應系數A(i);根據繪制出的氣壓響應函數(圖6),可見函數后半段具有典型的非承壓含水層特征.

圖6 氣壓響應函數

最后,根據(14)式,求得每個時間對應水位的校正值,得到校正后的水位.同樣選取某一周的時間對校正前后的水位進行對比,如圖7所示.

圖7 反卷積回歸法校正前后水位對比

從消除氣壓效應后的水位變化來看,反卷積回歸法的消除幅度更大.此種差異產生的原因在于,反卷積回歸考慮了氣壓效應的滯后性,而線性回歸法只消除了對應時刻的氣壓影響.

3 討論

由于井水位變化與氣壓變化存在相似的周期性,即1/3日、半日和1日周期性(圖8(a)).文中采用快速傅里葉變換分別對校正前后的水位進行頻譜變換,并與氣壓頻譜和原始水位頻譜進行對比,可通過觀察兩者的頻譜圖,比較水位與氣壓在相同波峰處的峰值是否減小或者消除,由此評價和判斷氣壓效應的消除效果.若相應頻率上的峰值減小的程度或消除的數量越多,證明井水位氣壓效應的消除效果越明顯;反之,則氣壓效應的消除效果就相對較差.

用斜率法與Clark法計算出的氣壓效率值在數值上有較大差異,通過線性回歸法計算出了兩種氣壓效率下的校正水位,從校正后的水位數據來看,兩種方法均對氣壓效應進行了一定程度消除.從得到兩者校正水位后的頻譜圖(圖8)中看出,斜率法與Clark法在1、3 c/d(circle per day,日循環次數)處沒有有效消除掉氣壓效應的影響,而在2 c/d周期處均對水位中氣壓效應進行了削弱,從消除程度上看,Clark消除效果更好,這是因為Clark法考慮了其他因素的影響.

由圖8(b)所示,利用線性回歸法消除氣壓效應后,井水位僅在2 c/d處的峰值得到了削弱.經過反卷積法消除氣壓效應后,孔井水位在1、2與3 c/d處的水位峰值均得到了削弱,且在2 c/d處,即半日周期的峰值削弱得最為明顯.

圖8 水位改正前后對比頻譜圖

通過對比反卷積法與線性回歸法處理后的井水位值和水位頻譜圖波峰消除幅度,可以發現反卷積法消除氣壓效應對地下水水位的影響優于線性回歸法.其原因在于反卷積回歸法考慮了前24 h的氣壓變化影響,而線性回歸法并未考慮氣壓效應的滯后性.

此外,在頻譜圖8中1 c/d處,即1日周期的峰值消除效果并不明顯.分析原因可能在于影響地下水微動態變化的外界因素不止氣壓效應,植物的蒸騰作用以及固體潮等亦對地下水位產生影響,由于植物蒸騰作用和固體潮作用都存在明顯的1 d周期,所以有可能是植物蒸騰作用和固體潮作用對井水位變化產生的影響.

4 結論

基于垮梁子一潛水含水層中的監測井,討論氣壓效率求取和氣壓效應消除的不同方法,得出如下結論：

1) 用線性回歸法對氣壓效應進行消除,分別采用斜率法和Clark法求取氣壓效率,從頻譜分析結果來看,Clark法獲取的氣壓效率比斜率法更可靠.

2) 用線性回歸法和反卷積回歸法對潛層含水層井水位進行氣壓效應消除,從消除效果來看,反卷積回歸法很好地削弱了井水位1/3、1/2和1 d波峰,而線性回歸只能消除部分的1/2 d波峰,反卷積回歸法優于線性回歸法.