基于動態穩定域的車輛橫縱向穩定性協同控制*
叢森森,高 峰,許述財
(1.清華大學蘇州汽車研究院(相城),蘇州 215133;2.清華大學,汽車安全與節能國家重點實驗室,北京 100084)
前言
隨著感知技術和智能算法的發展,智能車輛(intelligent vehicle,IV)得到了迅速發展。通過完備的交通環境感知和精準的車輛控制算法,IV 可以有效地提升道路安全。從控制理論角度來看,車輛穩定控制的重點是運動學和動力學控制。車輛動態穩定性對車輛運動學控制有著重要影響,可進一步提升車輛安全性。因此,研制一套完善的車輛動態橫縱向穩定性控制器具有重要意義。
在理想橫擺角控制和電子穩定控制ESC等穩定控制理論中,基于穩定域的穩定性控制作為一種直觀可靠的方法得到了廣泛研究。通常車輛穩定域可以通過側傾指數等穩定性指標或相平面區域閾值來定義。基于穩定域的控制通常在車輛失去穩定狀態的臨界時主動干預,可由接近穩定域邊界的車輛狀態表示。因此,基于穩定域的控制既可開發出獨立的車輛控制方法,又可與其他控制目的相結合。
雖然基于穩定域的車輛穩定性控制方法已得到廣泛應用,但其在穩定性控制方面仍有一些不足。首先,雖然穩定域邊界被準確清晰的推演,但在實際應用過程中缺乏直觀簡便的描述。由于不同穩定域相對于不同車速和轉向角度可顯著移動,在面對不同轉向角度和車速時因缺乏直觀表達而難以實際應用。其次,雖然車輛穩定狀態由穩定域外被控制回穩定域內,但只有在車輛狀態離開穩定域后才觸發控制策略。對于IV 而言,即使是輕微或暫時不穩定的車輛狀態也會存在安全隱患。最后,在固定車輛動力學參數基礎上,車輛穩定域近似不變,基于不同車況下的動態穩定域對車輛進行動態限幅控制能有效降低車輛失穩的可能性。
因此,為解決這些不足,設計了基于動態穩定域的橫縱向穩定性協同控制策略。本文結構如下:第1 章介紹所采用的車輛動力學和輪胎模型。第2 章中,首先分析車輛橫向穩定性,其次,基于基礎穩定域偏移設計動態穩定域,并基于動態穩定域進行動態限幅控制修正穩定域;最后,提出一種輔助前輪轉向控制(auxiliary front-wheel steering control,AFC)和DYC 設計動態滑膜橫縱穩定控制模型。第3 章中,通過Matlab/Simulink 與CarSim 聯合仿真驗證所提車輛橫縱穩定控制算法的有效性。
1 車輛動力學與輪胎模型
1.1 車輛橫向動力學
令、V、V和分別為車輛質量、縱向速度、橫向速度和橫擺角速度,F(=fl,fr,rl,rr)分別為車輛4 輪橫向力,為前輪轉角,為從質心到前輪軸距離,為從質心到后輪軸距離,為輪距的一半,F為AFS 產生的側向力,為DYC 產生的偏航力矩。則四輪車輛動力學模型如圖1所示。
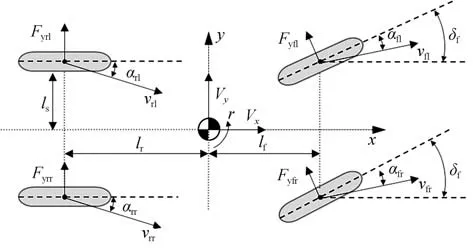
圖1 四輪車輛模型
車輛橫向穩定性分析和控制設計均采用四輪車輛動力學模型。具有狀態變量V和的車輛橫向動力學如下所示。
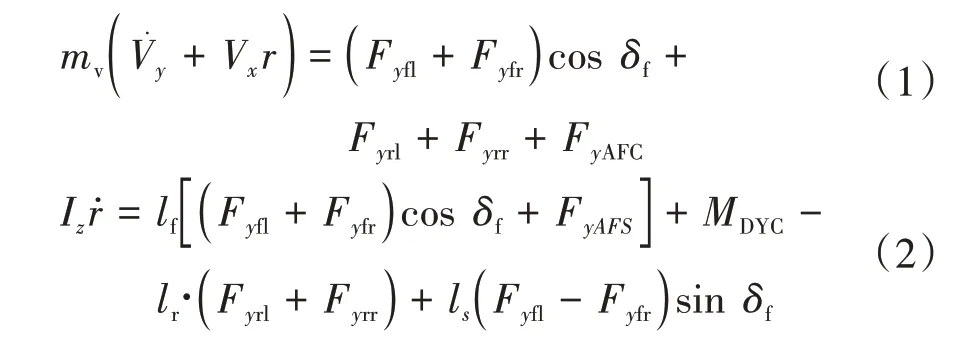
在研究極端條件下車輛橫向穩定性,特別是當輪胎側向力在大側偏角下飽和時,輪胎橫向力不能通過線性近似計算。因此,輪胎側偏角的計算應與車輛前輪轉向角保持相同。

1.2 二維LuGre輪胎模型
本文中采用一種改進的二維LuGre 輪胎模型,其優點是能夠準確地描述輪胎的非線性耦合力,且模型參數易于標定。通過改進的二維LuGre 輪胎模型進行側向力計算。


假設路面附著系數可以估計。為保證所提控制方法的有效性,采用與仿真中使用CarSim 輪胎模型相同的LuGre 輪胎模型進行標定,則輪胎模型間的一致性對比如圖2所示。
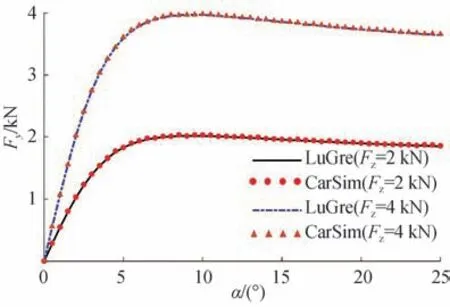
圖2 LuGre和CarSim輪胎模型橫向力對比
2 動態穩定域分析與穩定控制
2.1 基于投影法的橫向穩定性分析
在考慮橫縱向穩定性和輪胎特性基礎上,本文根據文獻[20]和文獻[25]中的車輛橫向穩定域,分析車輛橫向穩定性并設計相應的穩定性控制策略。
通過對車輛操縱穩定性和輪胎穩定性的綜合評價,利用局部線性化方法估計得出上圖車輛橫向穩定域。相較于文獻[10]~文獻[12]中等其他車輛穩定性評價標準,本文車輛穩定域更為全面。并且,通過合理的控制器設計可保證車輛穩定性和操縱性能。
如圖3 所示,在V=25 m/s、=0.75 且=0時,車輛橫向穩定域由V-閉合不規則相平面表示。穩定域由4 個邊界組成,根據不同車輛操縱穩定性標準,其中兩個邊界定義為轉向過度邊界,另兩個邊界定義為轉向不足邊界。邊界關于原點近似中心對稱。穩定域受V、和的影響而變化。
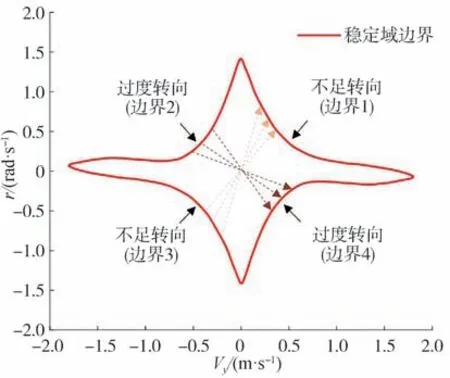
圖3 車輛橫向穩定域估計[20]
給定上圖穩定域,可以通過計算車輛狀態點(V,)和區域邊界之間的相對距離來分析車輛橫向穩定狀態。由于穩定域的邊界不規則,現有分析方法不適用,因此,提出一種投影法來進行穩定性分析,如圖4所示。
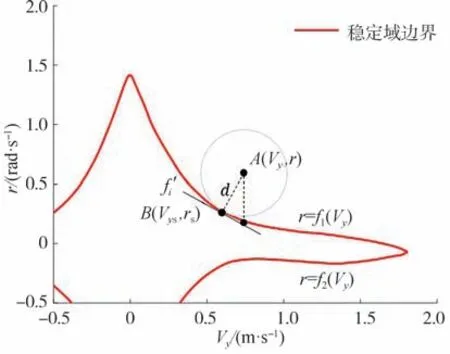
圖4 投影法與邊界最近點
由于邊界2 和3 分別與邊界1 和4 關于原點對稱,因此多項式= f(V),=1,2 即可描述穩定域邊界,在計算最近邊界點(V,)時,有
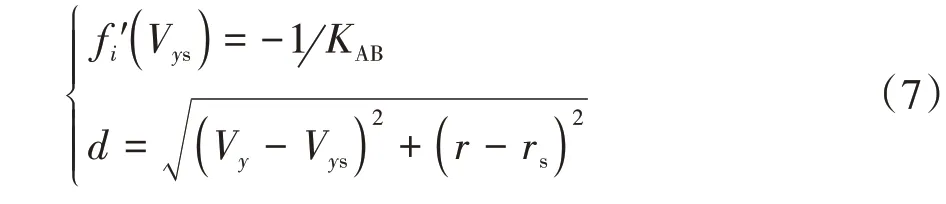

判斷車輛失穩方法如表1 所示。穩定域內任意點到穩定域邊界最短距離為
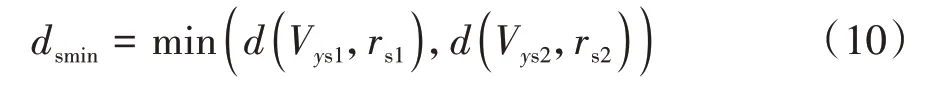

表1 基于穩定域的車輛失穩判斷方法
2.2 基于基礎穩定域偏移的動態穩定域設計
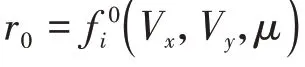
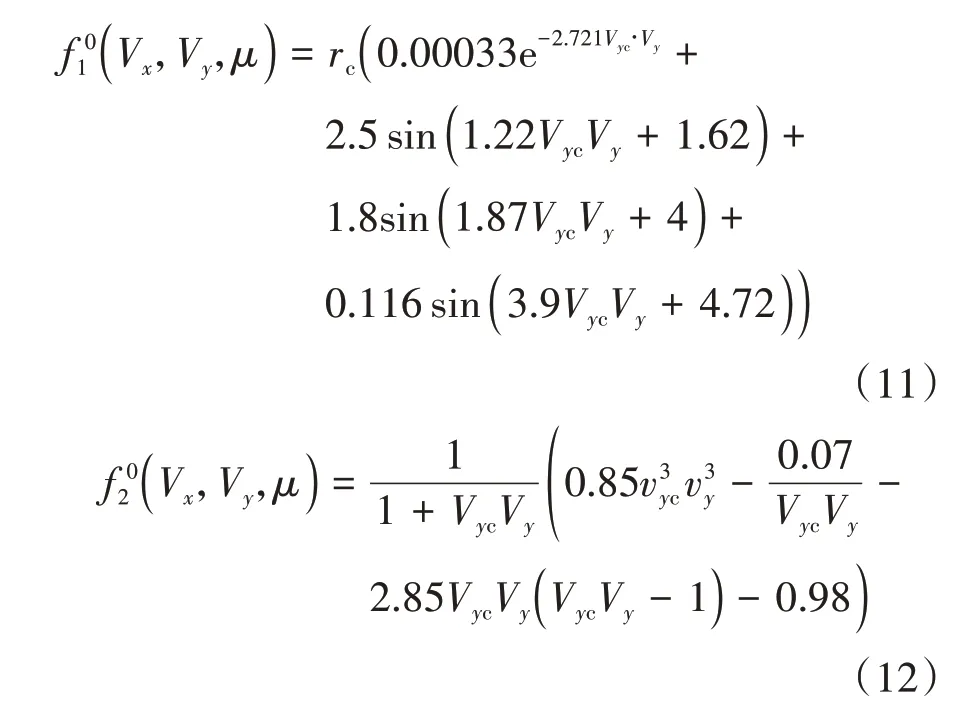
式中和為動態穩定域控制系數,=1.1,=1。橫縱向域穩態修正系數、V為
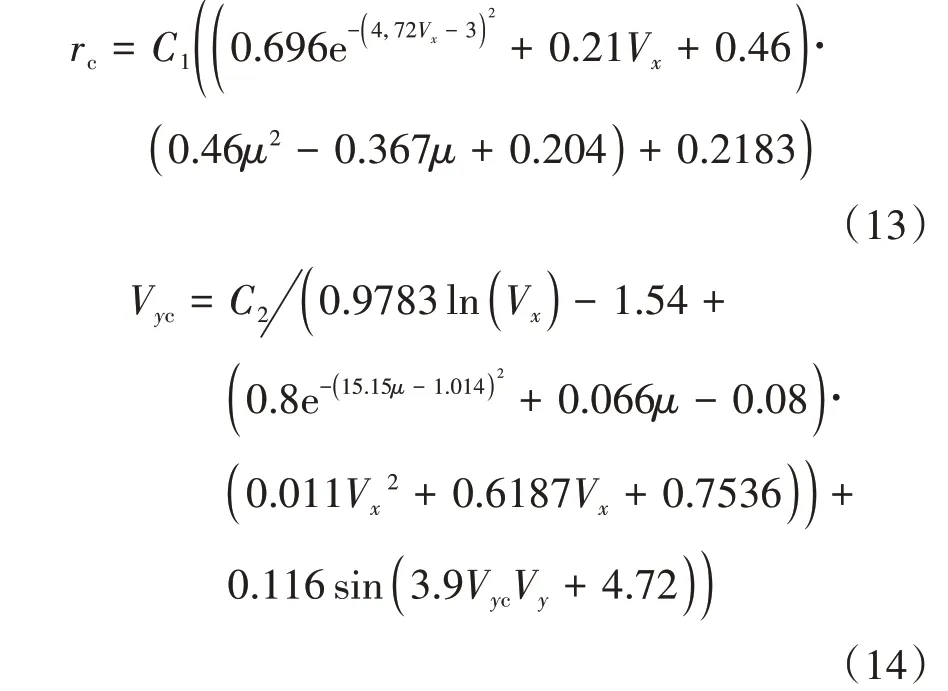
且當V<0 令V=0。當V和一定時,和V為常數。
為使車輛在臨界穩定域仍然可控,通過和將穩定域適當縮小,如圖5 所示。和將原動態域適當縮小為虛線所示的動態域。在實際控制過程中,適當的動態域縮小使穩態控制算法提前介入,有利于車輛實時穩定性響應。

圖5 修正的動態穩定域邊界
當V和一定時,動態穩定域邊界=f(V,V,,)可表示為

2.3 縱向穩定性限幅控制
平衡點能準確反映車輛的可控狀態。若平衡點越趨于離開甚至不在動態穩定域中,則表示越不能回到穩定點。因此,平衡點是否在穩定域內能直接說明車輛的可控性。


圖6 不同轉角的動態穩定域平衡點



式中為期望前輪轉角。則期望減速度:
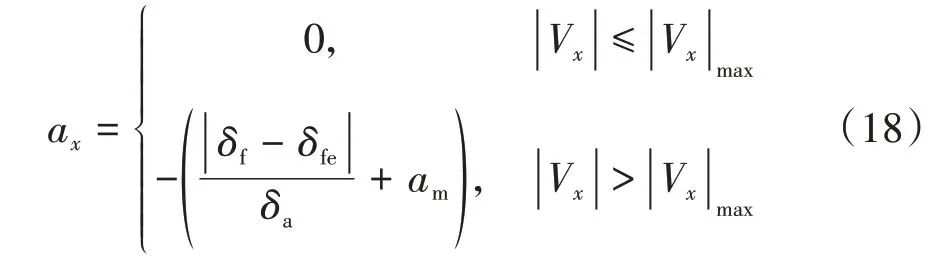
式中:為轉角修正系數,間接決定轉向角速度;為最小制動常數。
2.4 滑模橫縱穩定控制
當不可控因素干擾致車輛失穩,即車輛狀態點超出動態穩定域邊界時,根據(V,)對車輛進行輔助前輪轉角控制和橫擺力矩控制,使得車輛趨于穩定狀態。
設計滑模面:
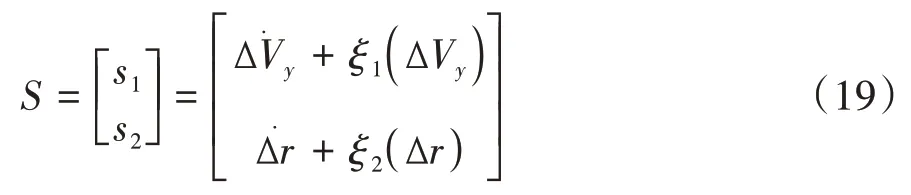
式中和為正常數。
設計趨近率為
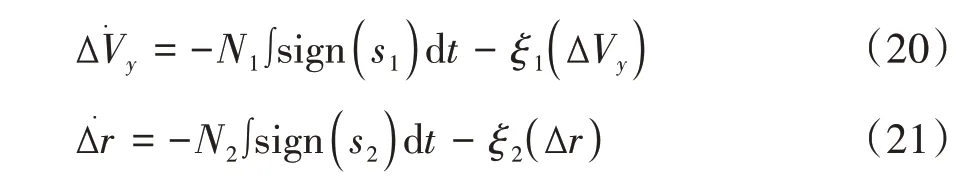
定義Lyapunov 函數為=/2 >0 并代入式(19)得:
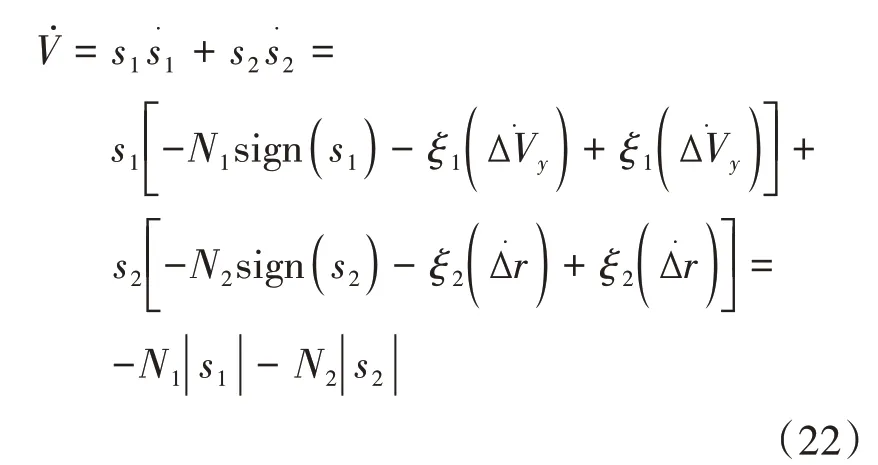
將趨近率代入動力學方程得:

前輪轉角主動抵消量:
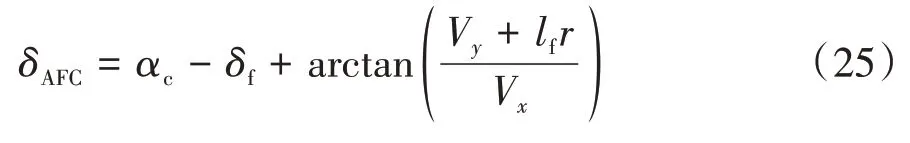
式中:由車輛總橫向力F+ F+ F代入輪胎橫向力方程反求解出α;δ<3°。
車身橫擺力矩控制4輪制動力:
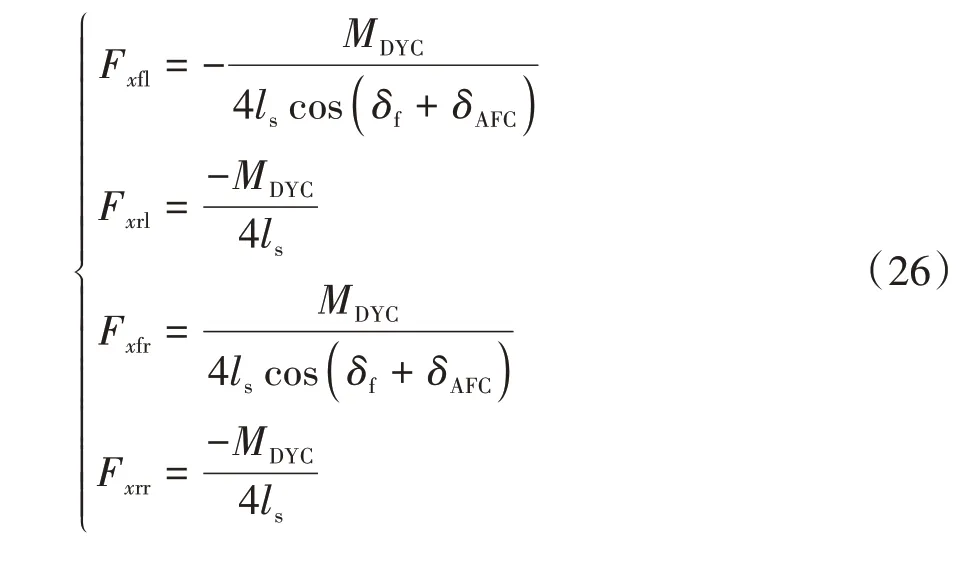
3 仿真與分析
在橫縱向控制過程中,為驗證基于動態穩定域的車輛穩定控制設計,分別在Matlab/Simulink 仿真環境中設計高速轉向場景和高速雙車道軌跡控制場景,聯合CarSim進行仿真控制。

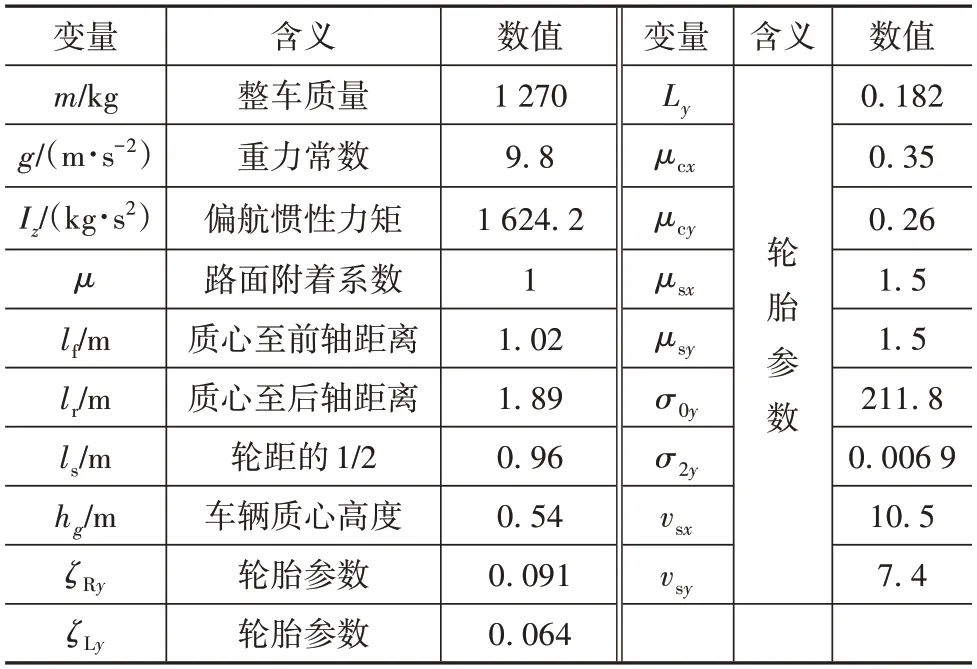
表2 車輛和LuGre輪胎模型關鍵參數
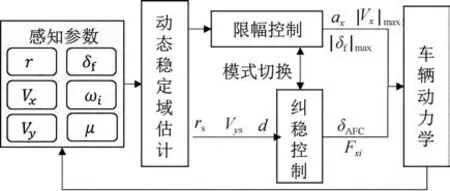
圖7 車輛穩定性控制流程
3.1 高速轉向穩定控制
車輛高速行駛時,不可靠的轉角輸入直接影響車輛的橫向穩定性。高速轉向場景中,通過前輪轉角的階躍輸入觸發轉角限幅控制,使得車輛在安全的前輪轉角下進行轉向。
設計初始車速為120 km/h,=0.8,對車輛設計的前輪轉角輸入和實際前輪轉角如圖8 所示。設計的前輪轉角下,若車輛無穩定控制,則會出現因操作不當造成的車輛失控或側翻;在限幅控制模式下,車輛根據車速計算出允許的極限前輪轉角輸入。實際車輛穩定域軌跡如圖9所示。
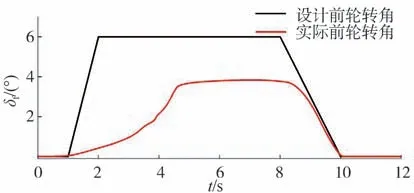
圖8 高速轉向場景前輪轉角輸入
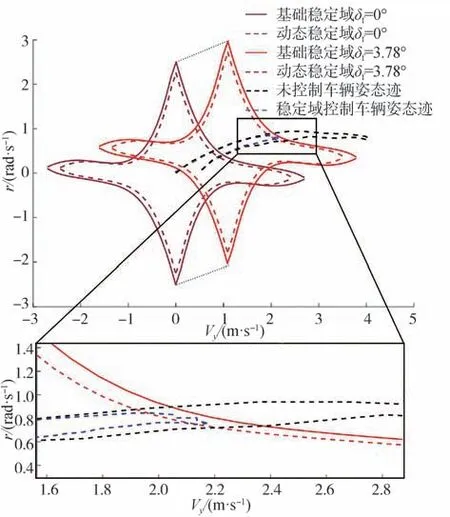
圖9 高速轉向穩定域軌跡圖
穩定域軌跡中,由于在初始速度下無制動和加速控制,動態穩定域邊界隨車速的緩慢降低略有變化。因此,允許的前輪轉角輸入動態增加。
3.2 高速雙車道軌跡控制
車輛在高速行駛時,若必須按照道路允許的區間行駛,則車輛必須優先滿足前輪轉角輸入控制。僅進行限幅控制無法滿足車輛穩定性需求。因此車輛進入縱向協同穩定控制。設計初始車速仍為120 km/h,在期望軌跡下進行前輪轉向輸入,對車輛進行橫縱協同穩定控制。設計前輪轉角輸入如圖10所示。

圖10 設計前輪轉角輸入圖
在設計前輪轉角輸入下,利用動態穩定域約束下的滑膜穩態橫縱向控制得出車輛軌跡如圖11所示。
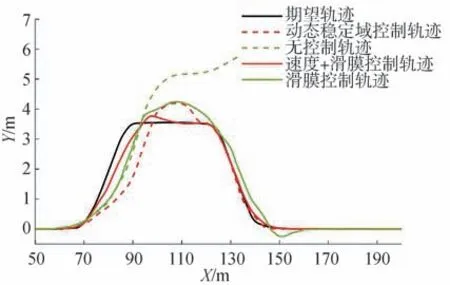
圖11 雙車道軌跡對比
圖11 中,無控制的車輛趨于失控,而基于動態穩定域的滑膜橫縱控制的車輛軌跡能良好的滿足車輛理想軌跡需求。
圖12 為橫縱協同穩定控制的實時車速,在期望軌跡下,前輪轉角輸入后使得縱向控制降低車速,以滿足轉角的控制需求。
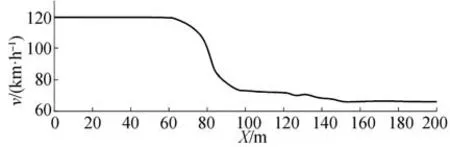
圖12 雙車道場景穩定控制的實際車速
動態穩定域會隨前輪轉角和車速的變化而變化,其穩定域邊界如圖13 所示。圖中,無約束的傳統滑模控制車輛姿態跡已超出穩定域邊界,車輛短暫處于失穩狀態。基于動態穩定域的橫縱控制姿態跡穩定的處于穩定域邊界內,雙車道軌跡控制理想。

圖13 軌跡控制穩定域圖
4 結論
本文中提出一種基于動態穩定域修正的車輛橫縱穩定綜合控制方法。首先,為分析基于基礎穩定域的車輛穩定性狀態,提出一種投影法的車輛穩定性分析方法。該分析方法可實時應用于車輛橫縱向穩定性控制。其次,根據基礎穩定域設計偏移指數的動態車輛穩定域。根據動態穩定域設計縱向加速度控制策略。最后,基于動態穩定域提出AFC 和DYC相結合的動態滑模控制。通過選取以動態裕度為滑膜面的穩定區域邊界設計車輛橫縱向穩定控制模型,保證了車輛軌跡始終控制在所采用的穩定區域。通過Matlab/Simulink 和CarSim 的聯合仿真,驗證了基于動態穩定域的車輛橫縱向穩定性控制方法的有效性。在實際車輛橫縱協同控制應用中,精確的輪胎模型標定直接決定控制模型的有效性和魯棒性。基于車身垂向穩定性的動態穩定域的控制設計將在今后的工作中完成。

