車用動力電池散熱管理的熱特性建模綜述

馬正偉，王 正,2

(1.深圳技術大學城市交通與物流學院，廣東深圳 518118；2.深圳大學機電與控制工程學院，廣東深圳 518060)

電動汽車動力電池的熱安全問題除了與動力電池本身熱特性有關外，還與電動汽車動力電池熱管理系統的散熱效率不足有關[1]。整體來看，現階段應用的車用動力電池熱管理系統能夠有效控制電動汽車在日常使用時充放電倍率所產生的溫差，但在長時間、多次循環、高倍率的充放電使用狀態下，在動力電池組內部仍然存在由于熱管理系統的散熱效率不足所積聚的大量熱量，導致電池溫度急劇上升和出現電池組內溫度梯度過大的問題，以至于電池組整體性能下降，甚至發生熱失控[2]。

針對電動汽車熱管理系統效率不足的問題，很多學者通過實驗、仿真建模等手段開展了廣泛的研究[3-5]。實驗研究容易受到設備成本、實驗周期、周圍環境等因素的影響[4]。相對而言，仿真建模由于具備成本低、周期短、可重復性好、改進方便等優勢，逐漸成為研究的主流手段[5]。根據傳熱散熱機理構建具有針對性的數值模型，該模型可以準確計算出散熱系統的效率，進而對散熱系統進行針對性的優化。本文圍繞動力電池熱管理系統的散熱方式，總結了近年來散熱系統建模的研究進展。

1 熱管理策略模型

電池組內部的熱量傳遞及耗散主要通過流體流動的方式進行，流體流動要受到物理守恒定律（質量守恒定律、動量守恒定律和能量守恒定律）的支配。上述物理守恒定律對應的控制方程能夠反應單位時間、單位體積內物理量的守恒性質。為了便于對各控制方程進行分析，并用同一程序對各個控制方程進行求解，式(1)建立了各控制方程的通用形式[6]：

式中：? 為通用變量，可代表u、v、w、T等求解變量，u、v、w是連續方程和動量方程中速度矢量在x、y、z方向的分量，T是能量方程中的溫度；Γ為廣義擴散系數；S為廣義源項。式中各項依次為瞬態項、對流項、擴散項和源項。源項是一個廣義量，對于特定的方程，有特定的形式。一般情況下，不屬于非穩態項、對流項和擴散項的成分均可放到源項中。在能量方程中，源項是化學反應和體積熱相關的項。能量方程中，源項的存在可以集中反映熱量的動態變化，并使得模型更精確，但也可導致方程數學性態的復雜，從而產生收斂困難、迭代不穩定等問題。源項也可簡化，如在研究針對性問題時，假設其處于不生熱或無熱量傳遞的條件，可將源項忽略。

不論是空氣冷卻模型、液體冷卻模型還是相變冷卻模型，在利用有限體積法對模型進行熱仿真時，都會用到上述守恒定律，通過質量守恒方程、動量守恒方程和能量守恒方程計算出散熱管理系統的冷卻效率，模擬電池組的生熱/散熱情況，觀察電池組內部的溫度，最終得出研究結論。

1.1 空氣冷卻模型

空氣冷卻，即利用冷卻空氣流經電池表面通過對流換熱的方式將電池組的熱量帶走，是目前最為常見、成本最低，也是應用最為廣泛的散熱方式，但由于空氣換熱系數低，存在換熱效率不足導致電池模組出現溫差較大的問題[7]，且在大功率放電時，難以將電池維持在理想的溫度范圍。由于空氣經過壁面產生的摩檫作用引起氣流相互干擾、混摻的現象，稱之為湍流，其速度和壓力等物理量在空間和時間上均具有隨機性質的脈動值。因此，在對空氣冷卻方式熱管理系統進行較為精確建模時，需建立湍流模型。

Zhang 等[8]在搭建空冷數值模型時，借鑒Li 等[9]的控制方程，即湍流動能方程和湍流動能耗散方程，如式(2)～(3)所示，其考慮了壁面傳熱湍流影響，能夠體現出湍動能和湍流耗散所攜帶的熱源。

針對在數值計算中運用有限體積法導致流體界面與固體壁面的節點不一一對應的問題，劉霏霏[10]建立了熱-流耦合傳熱模型，用于確保計算時流體和固體之間的數據傳遞，從而保證耦合面上的溫度和熱流連續。該模型驗證了熱-流耦合傳熱模型的高精度和高計算效率，表達式如式(4)所示：

式中：q為熱流密度；T為溫度；w 代表耦合面；f 代表流體區域；s 代表固體區域。

對于空氣傳熱問題的建模，主要還是對流換熱系數和空氣流動特性的確定。Kirad 等[11]在空氣冷卻系統建模后，引入冷卻效率因子β 用于評價模型，該因子很大程度上取決于電池之間的橫向間距，因為它影響著氣流沿模塊的流動特性和對流換熱系數，橫向間距的變化會引起面積變化影響壓降，而壓降又改變了供應冷卻空氣和β 所消耗的能量。其表達式如下：

式中：Δp為電池模塊入口和出口的壓降；U為空氣流速；μ 為空氣的動力粘度；D為電池直徑；St為電池間的橫向距離；Sl為電池間的縱向距離；Pr為普朗特數。

Liu 等[12]通過并行氣流冷卻系統對電池組的熱行為進行管理，如圖1 所示，Q為每個冷卻通道中的氣流速率。在二維模型的基礎上，將流阻網絡模型與瞬態傳熱模型耦合，利用耦合模型計算電池組中的溫度分布，并基于動量守恒定律建立流動阻力模型：

圖1 流動阻力網絡模型示意圖

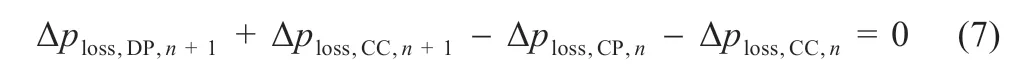
式中：CC 為冷卻通道；DP 為分散通風；CP 為聚集通風。該公式類似于基爾霍夫電壓定律，其每個路徑方向上的靜壓損失之和等于零，利用熱阻模型表示各個空氣流道內的壓降。

目前，空氣冷卻的建模主要針對的問題是流道內空氣湍流及與壁面的摩擦對壓降、動能的影響，針對這些問題，科研人員相應搭建了壓降模型、湍流模型及流固耦合模型，一定程度上解決了壓降、湍流等問題，但在實際空氣冷卻過程中這些因素是共同存在、相互影響的，在未來優化空氣冷卻模型時可考慮建立包含綜合影響因素的耦合模型。

1.2 液體冷卻模型

液體冷卻是指利用液體的流動特性帶走熱量。很多學者通過優化流道的結構設計以達到冷卻效率的最大化。液體冷卻效率受到眾多因素的影響，如管道內液體流速、溫度、流動方向、冷卻工質的性質等[13]。

Lai 等[14]通過仿真手段研究熱導結構的內部直徑、接觸高度和接觸角度對熱導結構的質量及冷卻性能的影響。假定電池模組除了通過冷板散熱外是絕熱的，搭建熱導結構的控制方程：

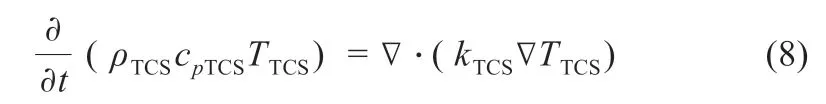
式中：ρ 為密度；cp為比熱容；T為溫度；k為熱導系數；TCS 為熱導結構。完整的能量方程應為：瞬態項加對流項等于擴散項加源項，針對研究的問題和在熱導結構中對流較小，式(8)只考慮熱導結構的瞬態項和擴散項。

在建模時耦合電池熱特性時，以往的控制方程直接將電池生熱量作為源項，但在實際熱量傳遞過程中，往往避免不了熱量的丟失。Chung 等[15]將冷板吸收的電池熱量作為源項，建立了相對精確的電動汽車熱管理系統冷板模型，其控制方程如下：

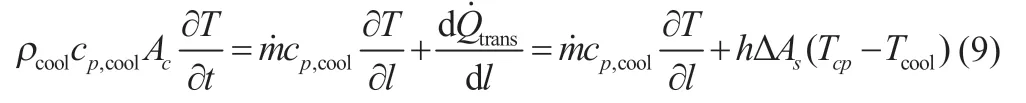
電池模組冷板的對流傳熱系數h可以由Gnielinski 相關性獲得：

式中：Nu為冷板的努塞爾數；Prcool為冷板的普朗特數；L為冷板的幾何特征長度，垂直于傳熱面的尺度；k為流體的導熱系數；fcool,0和γ 分別表示圓管的摩擦系數和矩形通道的長寬比。

液體冷卻不僅要考慮散熱效果，同時還要兼具最佳冷卻結構、管道內最佳流量、最小能量損耗等。E 等[16]通過搭建蛇形管道的液體冷卻模型，將模型分為熱阻模型和壓力損失模型且建立相應的目標函數f1和f2，并通過算法優化得到最佳的冷卻結構。壓力損失模型考慮到液體在管道內的摩擦損耗和附加損耗，其表達式如下：

式中：Δpf為摩擦壓力損失；λ 為摩擦損失系數；ρ 為流體密度；lp為管的長度；dh為管的水力直徑，dh=2lwri/(lw+ri)；Δpb為彎管總過量壓力損失；ξ 為過量損失系數。根據傳熱理論，熱流為固定值時，熱阻越小，制冷效果就越好。熱阻模型根據熱傳遞理論將熱阻分為傳導熱阻和純熱阻，其傳熱過程和熱阻的示意圖如圖2 所示。Ra、Rb為進出口處和直管處不同形式的熱阻，R1～R14為不同部位處的熱阻，其相互關系如下所示：

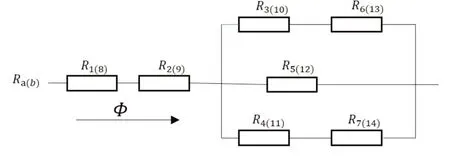
圖2 傳熱過程和熱阻的示意圖

利用Ra、Rb建立冷板熱阻模型，表達式如下：

Deng 等[17]為了在低流動狀態下獲得最佳熱性能，將流體域的表面摩擦系數f和對流傳熱系數h作為目標函數，基于進化算法對電池組液冷系統進行優化設計，使得對流傳熱系數最大，表面摩擦系數最小，并通過建立驅動冷卻液的泵功率P模型來計算流動阻力，表達式如下：

式中：Δp為總壓降；ρl為流體密度；u為流體速度；Dh為通道的水力直徑；L為通道長度；n為通道數；Qconv為對流散熱量；Aw為對流傳熱面積；Tw為通道壁的溫度；Tl為通道內流體的溫度；qm為質量流率。

Liu 等[18]利用冷卻能力更強且適應極端條件的液態金屬作為冷卻劑，提出一種可變流速策略，根據充電狀態和特定的操作條件選擇最佳流量，通過建立仿真模型得到結論：在一定體積流量范圍內，管道的數量較少但流速較高的結構具有較高的冷卻性能。其模型計算了信號銅管傳遞的熱量，如下所示：

式中：qpi是信號銅管傳遞的熱量；ρl是管中液態金屬的密度；Vl表示管中液態金屬的體積；ΔTl表示入口和出口處的液態金屬之間的溫差；cpl是管中液態金屬的比熱容。

針對液體冷卻系統的最佳熱性能、最佳冷卻結構或穩定充放電狀態下的最佳流量問題，利用流體域的表面摩擦系數和對流傳熱系數等作為目標函數，通過相應算法進行優化并取得良好成果。利用電路模型或熱阻模型來模擬能量損耗，因其結構自由、計算量較少等特點，可能成為未來散熱冷卻建模的主流手段。

1.3 相變材料冷卻模型

相變材料冷卻(PCM)是利用相變材料物理狀態的改變(即熔化或者升華)來吸收或者放出熱量，以達到控制電池箱內溫度的目的。當電池溫度達到相變材料的相變溫度時，相變材料發生相變，吸收電池散發的熱量，可以長時間保持電池的溫度在相變溫度范圍內，從而可以減少電池組的能量衰退[19]。

Klime? 等[20]將相變冷卻傳熱廣泛使用的建模方法進行總結分類，分為焓法和有效熱容法。焓法將焓定義為溫度的函數，使用熱力學公式來描述相變過程中顯熱和潛熱之間的關系，表達式如下：

式中：h為焓熱；ρp為密度；Tref為參考溫度；c為熱容；L為熔化熱；fs是固體部分；θ 為積分變量；ρpc為單位密度物體改變溫度時吸收或釋放的內能；ρpL[(?fs)/(?θ)]是固體部分單位體積因熔化所吸收的熱量。再將焓h帶入到式(22)控制方程中，求解相變傳熱問題。

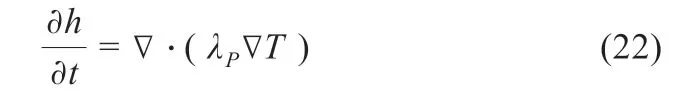
式中：t為時間；λP為導熱系數；?是微分運算符。焓法可同時適用于快速和漸變的相變，且計算效率高，但對于過冷問題計算較為困難[21]。有效熱容法與焓法十分相似，有效熱容法利用有效熱容系數來代替焓，公式如下：

式中：ceff為有效熱容系數。有效熱容法公式簡單，但想要達到理想的精度，計算時需較小的時間步長和精細的網格，與焓法相比，計算成本較高[21]。

Ling 等[22]較早對相變材料冷卻的熱力學過程進行了建模，此模型引入PCM 的相變權重系數β，考慮了相變材料的狀態對潛熱的影響，對后來相變冷卻建模起到一定的指引作用，表達式如下：

式中：ρ為相變材料的密度；λ為相變材料的導熱系數；T為相變材料的溫度；h為相變材料的比焓；ΔH為相變過程中的焓變；γ為相變材料的相變潛熱；Tm為相變材料的相變溫度點。

Wang 等[23]在研究基于泡沫銅和石蠟復合相變材料的新型無源熱管理系統(無源等于耦合空氣冷卻)的過程中，進行仿真實驗，在Ling 等[22]的基礎上對PCM 的相變權重系數進行優化，使得模型更加精確，表達式如下所示：

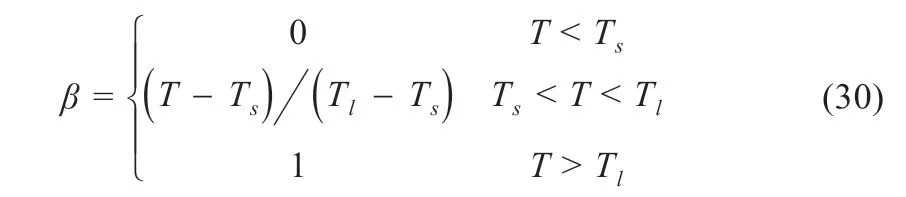
式中：Ts和Tl分別是相變材料的凝固溫度和相變材料的液化溫度。

柔性復合相變材料通過減小接觸面之間的氣隙，從而提高表面傳熱能力，其材料的高導熱性是改善電池模組溫度均勻性的主要原因。Huang 等[24]采用有效熱容法對柔性復合相變材料進行數值模擬研究，引入隨溫度平滑變化的有效熱容δ，并耦合到控制方程中，表達式如下：

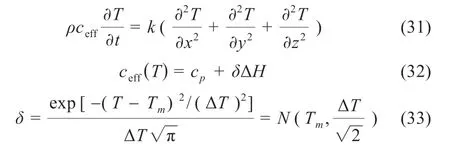
式中：cp為處在獨立狀態的比熱容；ΔH代表復合相變材料的潛熱；Tm為相變溫度；ΔT為相變溫度與電池溫度峰值之差的二分之一；N為正態分布。

相變材料的良好熱性能使之成為未來最為看好的熱管理介質之一，其建模方法被總結為焓法和有效熱容法。焓法可同時適用于快速和漸變的相變，且計算效率高，但對于過冷問題計算較為困難；有效熱容法與焓法十分相似，有效熱容法利用有效熱容系數代替焓，其公式簡單，但想要達到理想的精度，計算時需較小的時間步長和精細的網格，相比焓法，有效熱容法的計算成本較高，未來可在相變權重系數上進行改進，使其更加精確。

2 結論

電動汽車動力電池熱特性仿真以成本低、周期短等優點被發展，且在電池熱管理系統的設計方面能起到指引作用。本文從風冷、液冷和相變冷卻三個方面對該領域的模型進行闡述。

空氣冷卻因結構簡單，影響制冷效果的因素少，建立的模型較為精確，但每個模型針對的影響因素都不同。因此，未來可將其各影響因素進行耦合，搭建更為精確的空氣冷卻模型。液體冷卻在進行建模時，因其結構更為復雜，故建模時需考慮的影響因素更多，主要研究最佳熱性能、最佳冷卻結構或穩定充放電狀態下的最佳流量問題，模擬電路模型或熱阻模型可能成為未來建模的新興手段。相變冷卻由于其傳熱工質的特殊性，成為近年來研究的熱點領域，其冷卻建模方法被總結為焓法和有效熱容法，焓法的關鍵在于相變材料的狀態對潛熱的影響，而有效熱容法的關鍵在于關于溫度或其他因素的有效熱容函數的搭建。

總體來看，每種冷卻方式對動力電池的貼合度都不相同，對流傳熱系數的確定依然是精確建模的重點、難點，在確定對流傳熱系數方面可參考文獻[15]。雖然目前已取得大量的理論和成果，但動力電池熱特性模擬的研究還存在沒有考慮電池傳熱的源項或考慮恒定源項等問題，車用動力電池的熱管理還面臨諸多挑戰。