考慮碳排放的綜合能源系統“結構-型號-容量”優化模型

李國堂，宋福浩，陳杰，刁利，王永利，郭遠征，劉楨梁

(1.國核電力規劃設計研究院有限公司,北京市 100095;2.華北電力大學經濟與管理學院,北京市 102206)

0 引言

隨著碳中和目標的提出,構建清潔低碳,安全高效的能源體系日益迫切,發改能源規〔2021〕280 號文提出源網荷儲一體化和多能互補發展是提升可再生能源開發消納水平和非化石能源消費比重的必然選擇。 綜合能源系統具有縱向源網荷儲協調,橫向多能互補的優勢,是實現我國能源革命及“3060”雙碳目標的重要載體[1-2]。

合理的規劃及科學的調度策略是綜合能源系統降本增效的必要條件。 關于綜合能源系統運行優化模型的研究,其中,需求響應手段可充分利用用戶特征,通過“源-荷”互動的方式實現降本增效的目的。 文獻[3]綜合考慮了電-熱需求響應,構建以運行成本最低、能效最高的雙目標優化模型。 文獻[4]在考慮綜合需求響應的基礎上,構建綜合能源系統運營商與用戶、上級能源網的交互框架,引入勢函數構建了以各主體利益最大化為目標的綜合能源系統運行優化模型。 文獻[5]利用Charnes-Coope 處理綜合能效目標,實現綜合能源系統供需雙側協調優化。 在碳交易市場背景下,綜合能源系統可通過優化手段降低碳排放量以及碳排放成本,文獻[6-8]考慮碳交易機制,優化能源供給側設備出力及負荷側需求響應策略,平抑負荷波動,提升可再生能源的消納率,并控制碳排放總量。

由于綜合能源系統的建設成本較大,相比于綜合能源系統運行階段的優化,科學的規劃結果能夠節約更多的成本。 為解決源-荷雙側不確定性導致的規劃準確性下降的問題,文獻[9]研究了可再生資源不確定性處理辦法,構建了綜合能源系統的雙目標規劃模型;文獻[10]基于能源集線器(energy-hub,EH)模型,結合k-means 算法得到典型日負荷曲線,以上下界區間的方式描述負荷不確定性。 在綜合能源系統規劃方法的研究上,文獻[11]構建了三層規劃調度模型,包括預測層、規劃層和調度層;文獻[12]考慮虛擬儲能特性構建了區域綜合能源系統儲能規劃模型。 碳交易也逐漸引入綜合能源系統規劃優化的研究中,文獻[13]考慮綜合能源系統的低碳性以及建設時序,提出了一種基于階梯碳交易機制的園區綜合能源系統多階段規劃方法;文獻[14]建立了一種考慮碳排放懲罰因子的規劃模型,并針對碳排放因子進行敏感性分析。

現有文獻對綜合能源系統的規劃模型研究集中在場景特定[15]、設備型號特定的情況下對設備裝機容量優化。 因此,針對綜合能源系統建設時遇到的能源結構選擇、設備型號選擇、裝機容量優化問題進行建模。 首先,分析實例推理技術的基本流程,提出基于最近鄰法(K-nearest-neighbors,KNN)實例推理技術的能源結構優化模型;然后,構建“外層選型,內層定容”的雙層優化框架,考慮選型約束條件及容量優化約束條件,利用蟻群-遺傳算法相結合的智能求解方式對模型求解;最后,通過算例分析驗證模型在解決綜合能源系統規劃問題上的有效性。

1 協同優化框架

綜合能源系統能夠極大程度上利用能源耦合互補機理,降低能源消耗成本、提升綜合能效、降低碳排放[16]。

綜合能源系統園區建設的地理位置、用戶類型的差異性等特征導致了能源結構的多樣性。 同時,同種類型設備在型號、價格、性能等方面均有不同,這進一步提高了綜合能源系統規劃的復雜程度。 基于此,本文提出集“能源結構優化-設備選型優化-設備容量優化”為一體的協同規劃優化模型,如圖1 所示。

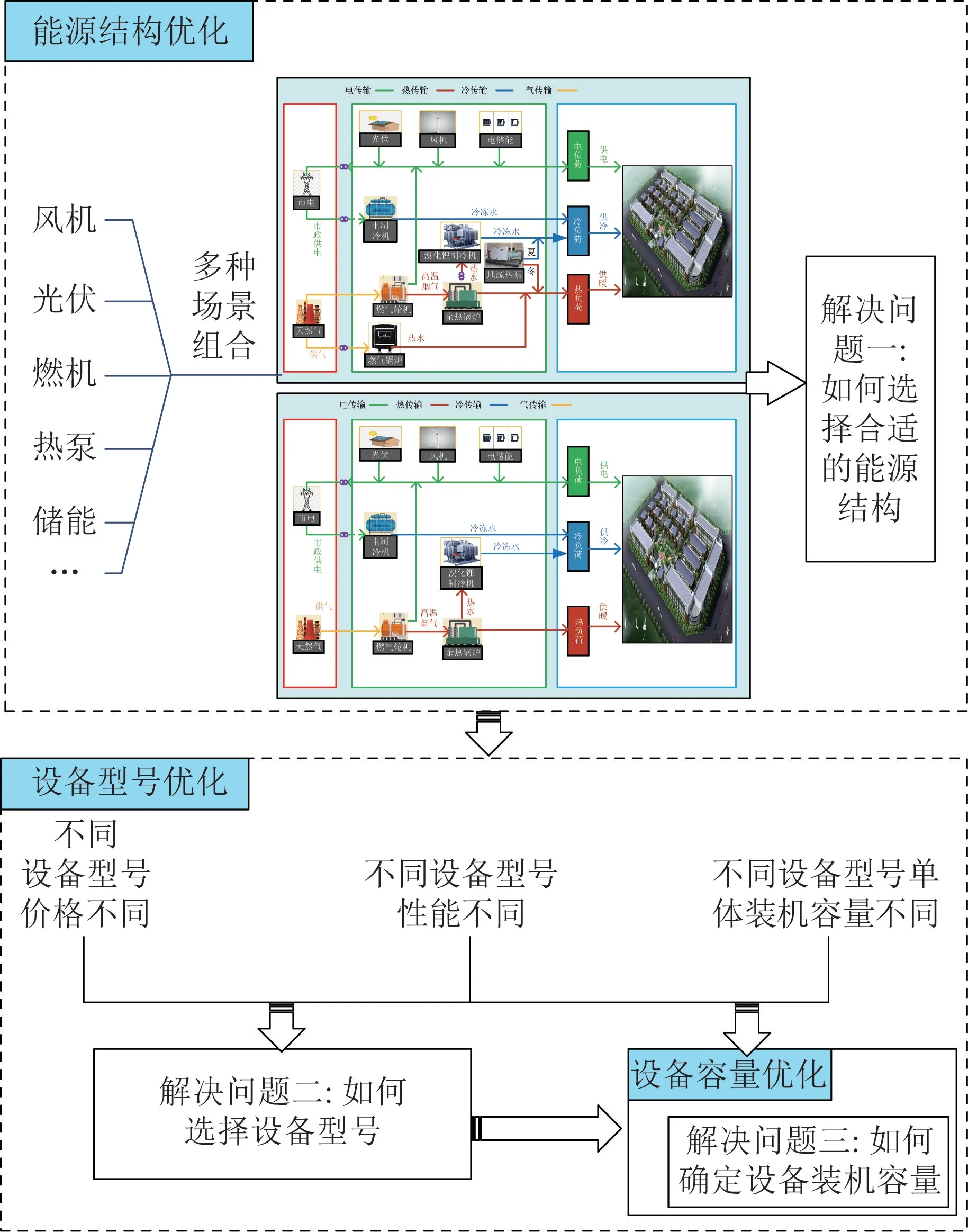
圖1 協同優化框架示意Fig.1 Illustration of the collaborative optimization framework

2 基于KNN 實例推理技術的能源結構優化模型

實例推理技術(case-based reasoning,CBR)[16-18]是利用已有的經驗解決新問題的一種方法,具有動態知識庫和增量學習的特點。 本文采用KNN 實例推理技術對綜合能源系統規劃的能源結構進行優化選擇,模型流程如圖2 所示。 典型特征因子庫見表1。

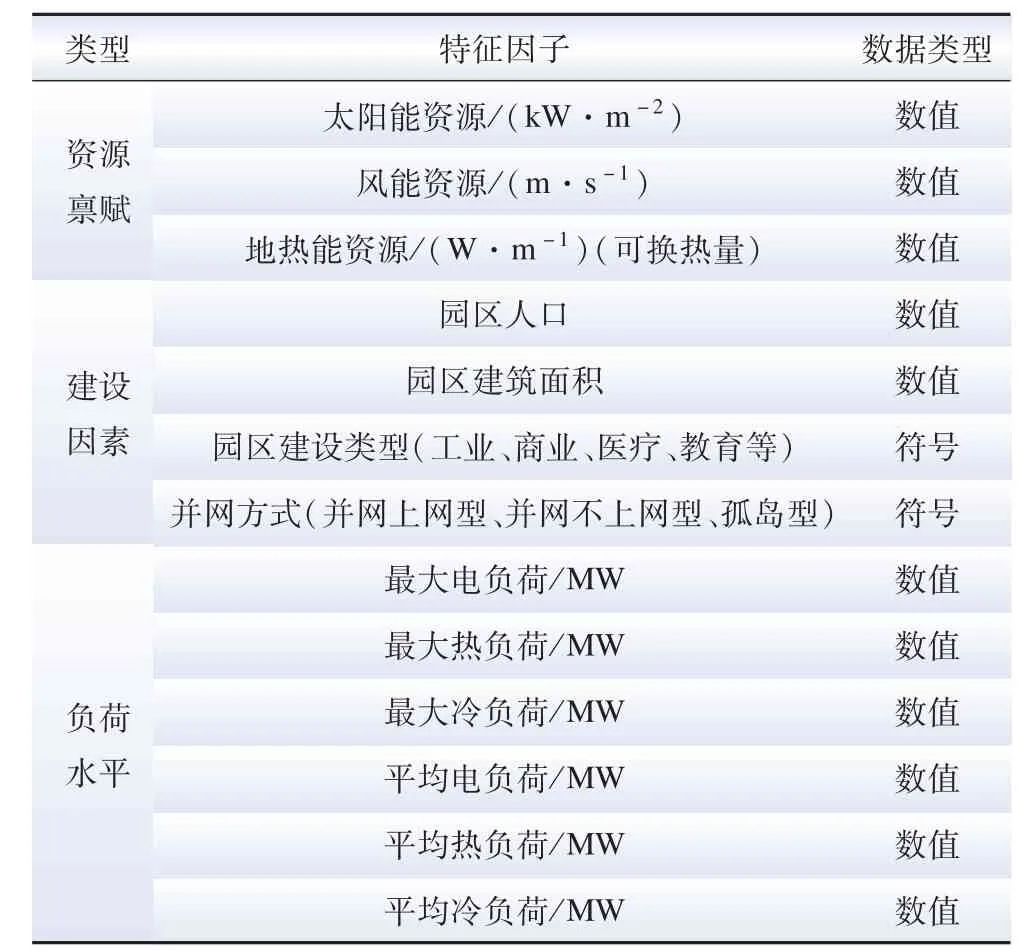
表1 特征因子Table 1 Characteristic factor

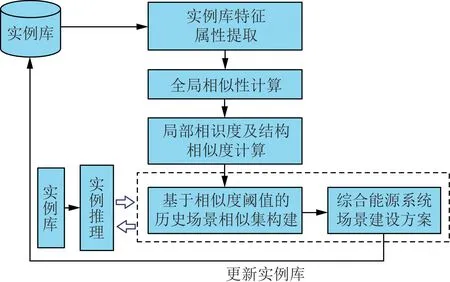
圖2 KNN 實例推理技術Fig.2 Case-based reasoning technology based on KNN

設S為實例庫中場景集合:

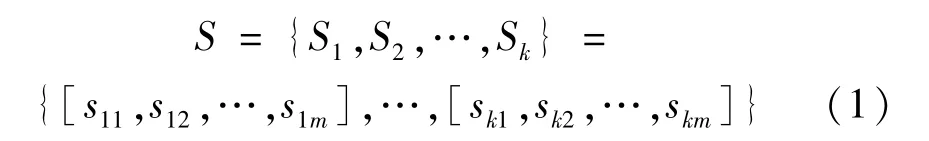
式中:Sk為第k個實例庫場景;skm為第k個實例庫場景中第m個供能機組類型。

設E為特征因子集合:

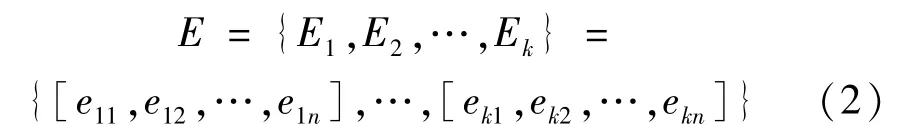
式中:Ek為第k個實例庫場景的特征因子集合;ekn為第k個實例庫場景中第n個特征因子。

擬規劃園區與實例庫場景之間的全局相似性計算公式為:

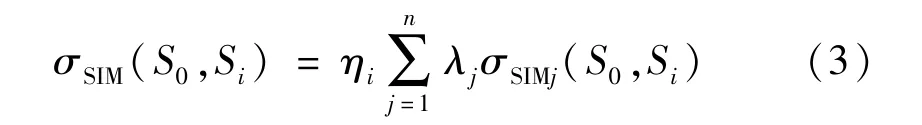
式中:σSIM(S0,Si)為S0與Si之間的全局相似度;S0為目標場景;σSIMj(S0,Si)為S0與Si之間特征因子j的局部相似度;λj為特征因子j的權重;ηi為S0與Si的結構相似度。σSIM(S0,Si)越接近1,代表S0和Si的全局相似度越大。

1)標準化處理。

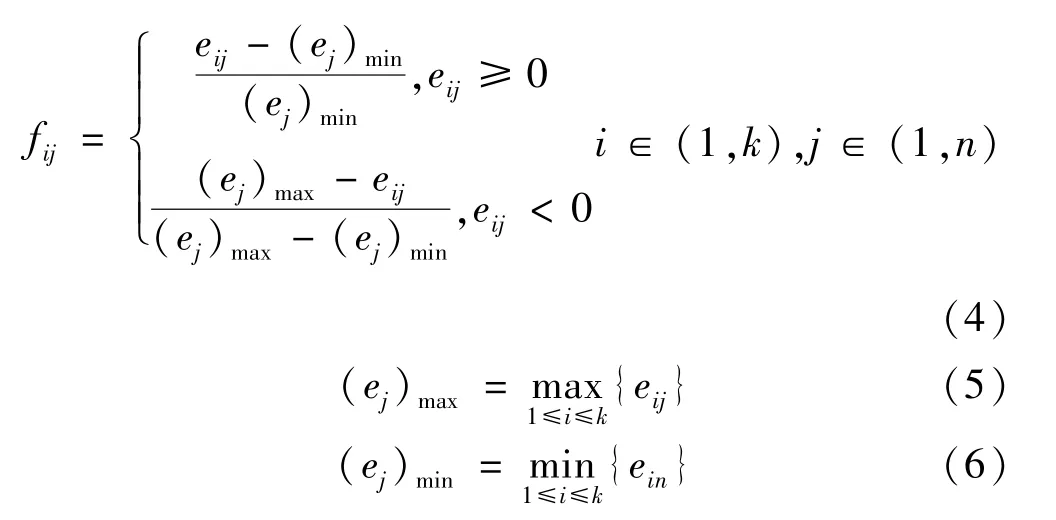
式中:fij為標準化后的特征因子值。

2)局部相似度計算。

步驟1:數值類型的特征因子通過距離計算法確定局部相似度。

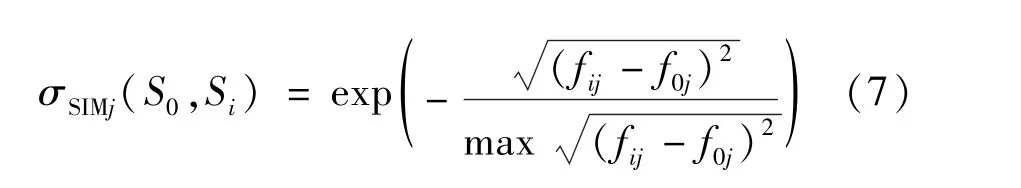
式中:max (fij - f0j)2為S0和Si的特征因子j之間的最大差值。

步驟2:符號數據局部相似度計算方法如下:

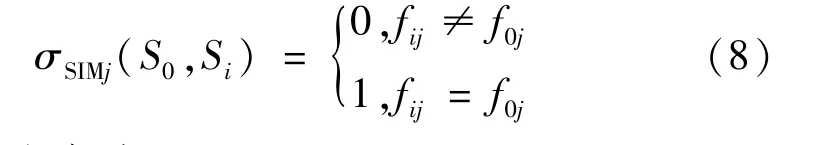
3)結構相似度。

步驟1:設S0非空特征因子為集合A,Si非空特征因子為集合B。

步驟2:計算I=A∩B和U=A∪B。

步驟3:計算I中所有特征因子權重總和,記為w1;計算U中所有特征因子的權重總和,記為w2。

步驟4:得到ηi=w1/w2。

4)能源規劃結構選擇。

為了提高能源結構選擇效率,以相似度閾值δ為判斷標準,δ越大,則代表選擇場景與目標場景相似度越高。δ計算方法為:

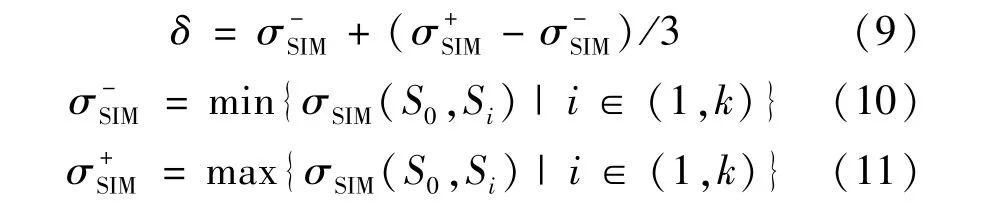
當σSIM(S0,Si) ＞δ,將Si作為可行規劃解。

3 “外層選型,內層定容”雙層優化模型

1)外層選型優化。

利用算法編碼的方式將設備型號庫信息傳遞至內層定容模型中。

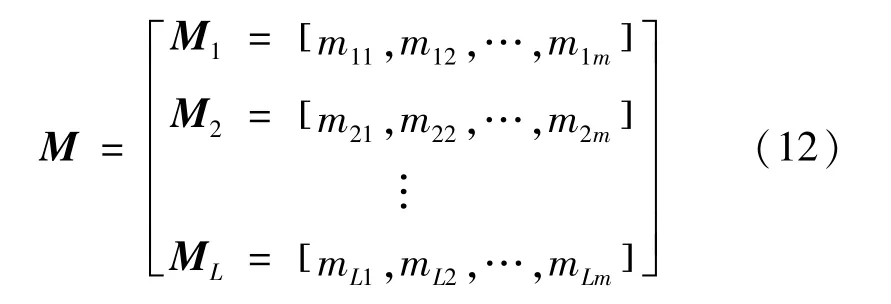
式中:M為設備類型編碼矩陣;M1為優化后能源結構第一種設備類型;L為設備類型的個數;mL m為第L種設備的第m個型號。

2)內層定容優化。

內層定容優化以資源容量約束、能源供需平衡約束為約束條件,求解設備最優裝機容量。 “外層選型,內層定容”雙層優化框架如圖3 所示。

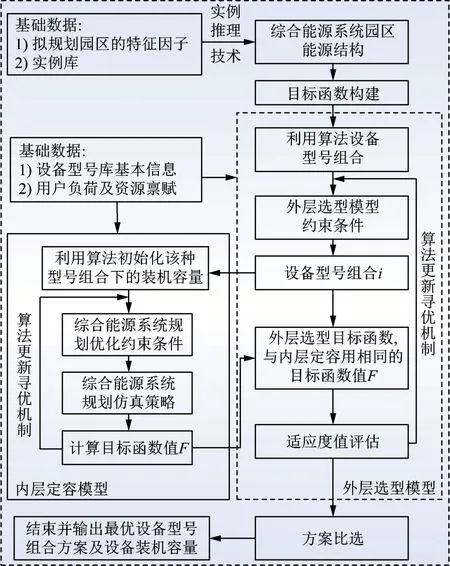
圖3 “外層選型,內層定容”優化框架Fig.3 Optimization framework of "outer layer selection, inner layer constant volume"

內外兩層均以全壽命周期總成本最低為優化目標,內層容量優化模型利用算法每迭代一次后,將其結果記錄在外層選型模型中。

3.1 目標函數

本文引入梯級環境交易機制引導綜合能源系統減少二氧化碳的排放,目標函數為:

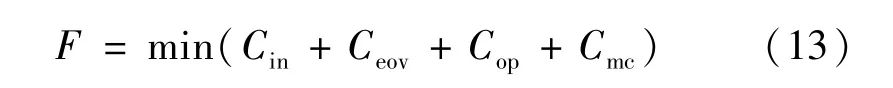
式中:Cin為初始投資的年等值成本;Ceov為系統全壽命周期內一年的碳交易成本;Cop為全壽命周期內年均運行成本;Cmc為系統全壽命周期內一年的運行維護成本。

1)初始投資成本。

初始投資成本主要考慮系統設備的購置費用,并將投資轉化為年化投資[19]。

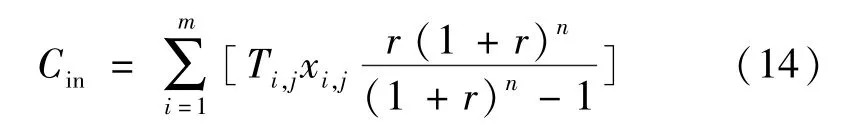
式中:xi,j為定容模型的優化變量,表示第i類設備中j型號的裝機臺數;Ti,j為設備的單臺購置費,元/臺,i由實例推理的綜合能源規劃結構確定,j由外層選型模型傳遞到內層定容模型中;r為基準折現率;n為壽命周期。

2)碳交易成本。

在碳交易機制的背景下,系統二氧化碳排放超過碳配額(基準碳排放量)的情況下,需要購買碳排放權[20]。

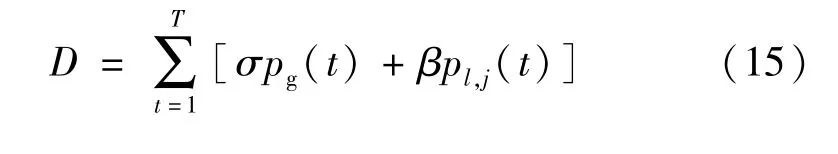
式中:D為基準碳排放量;σ為單位電量的基準二氧化碳排放;β為單位熱量基準二氧化碳排放;pl,j(t)為消耗天然氣設備l的出力;pg(t)為系統購電量。

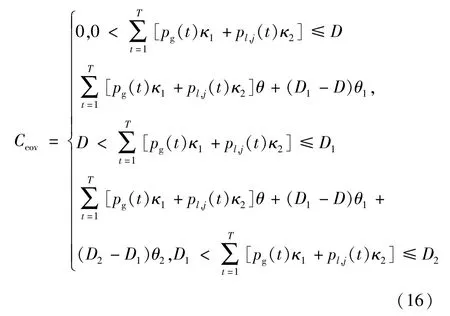
式中:D1、D2分別為階梯二氧化碳排放量限額;κ1、κ2分別為購電和使用燃氣產生的二氧化碳;θ為二氧化碳單價;θ1、θ2分別為階梯環境交易價格。

3)外購燃料成本。

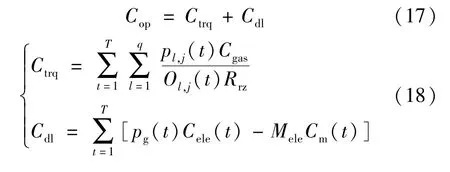
式中:Ctrq為天然氣消耗成本;Cdl為購電成本;Cgas為氣價;Ol,j(t)為設備的能效值;Rrz為天然氣的熱值,通常取10 kW/m3;Cele(t)為分時電價;Mele為系統售電量;Cm(t)為售電價。

4)設備維護成本。

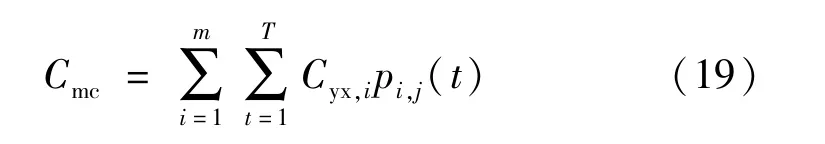
式中:Cyx,i為各個設備的運行維護成本;pi,j(t)為第i類設備中j型號設備模擬仿真時的出力。

3.2 約束條件

1)設備匹配約束。

若實例庫各場景中均建設A 機組與B 機組,則認為A 機組與B 機組具有匹配關系,并形成匹配關系矩陣Q。

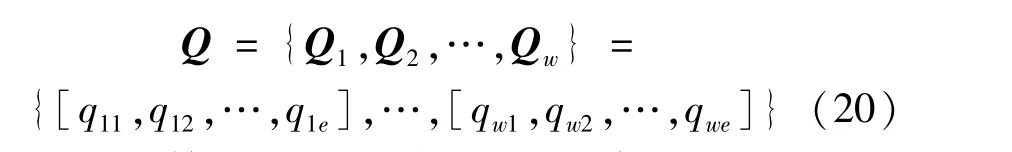
式中:qwe表示第w組匹配關系的e設備。

則優化模型需要滿足以下約束:

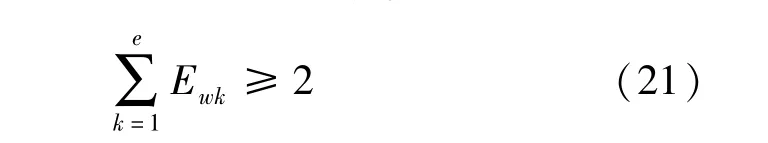
式中:Ewk表示Q中設備的被選擇狀態,若選中為1,未被選中為0。

2)設備互斥約束。

現在五芳齋的第一張面孔是“老字號”，它背后是“一味百年心”的美食匠心，第二張面孔則更顯生機勃勃，散發著互聯網時代的新銳氣質。

若實例庫各場景中A 機組與B 機組均不能同時共存,則認為A 機組與B 機組具有互斥關系,并形成互斥關系矩陣H。

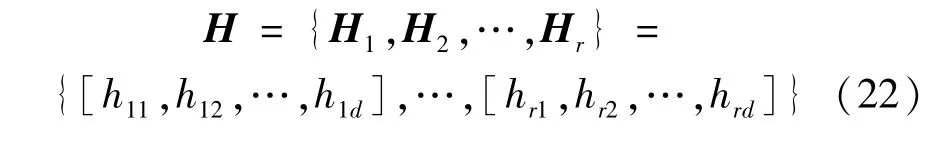
式中:hrd表示第r組匹配關系的d設備。

3)資源容量約束。 主要針對地源熱泵規劃時考慮的可換取熱量約束[21]。

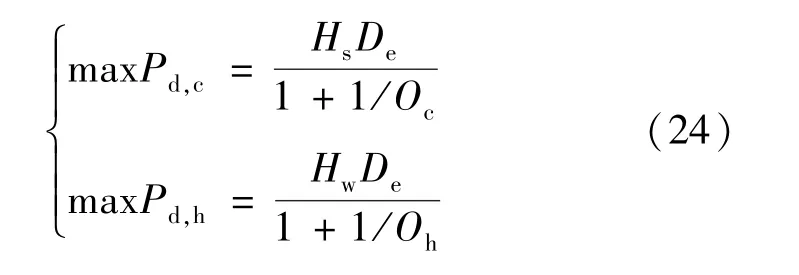
式中:Pd,c、Pd,h分別為地源熱泵的夏季制冷功率與冬季制熱功率;De為地埋管深度;Hs、Hw分別為地源熱泵夏季排熱工況下每延米井深的換熱量以及冬季取熱工況下每延米井深的換熱量;Oc、Oh分別為地緣熱泵供冷與供熱時的能效值。

4)能量平衡約束。 主要包括冷熱電系統的供需平衡[22]。

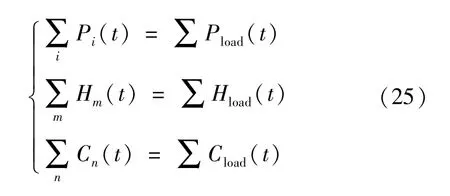
式中:Pload(t)、Hload(t)、Cload(t)分別為用戶的電、熱、冷負荷;Pi(t)為設備i的供電出力;Hm(t)為設備m的供熱出力;Cn(t)為設備n的供冷出力。

3.3 求解算法

設備型號優化過程類似于路徑選擇問題,利用蟻群算法進行求解[23],容量優化采用遺傳算法[24]。

4 案例分析

4.1 基礎數據及仿真結果

以我國西部某商業園區為例進行案例仿真。實例庫參數見附表A1、A2。 計算得到場景相似度如附表A3 所示,其場景相似度閾值為0.661,其中,S6與S16兩個場景與目標場景的相似度閾值大于0.661。

設實例庫中S6為場景1,其能源結構為:風機-光伏-地源熱泵-CCHP -燃氣鍋爐-電制冷-儲電;設實例庫中場景S16為場景2,其能源結構為:風機-光伏-地源熱泵-冰蓄冷-電制冷-電鍋爐-蓄熱式電鍋爐。

仿真設備參數見附表A4。 算法迭代曲線見圖4,仿真規劃結果見表2—4。 圖4(a)、(c)為外層選型算法迭代曲線,由于設備型號組合多樣,設置迭代次數為1000 次;圖4(b)、(d)為內層定容算法迭代曲線,迭代次數為100 次。

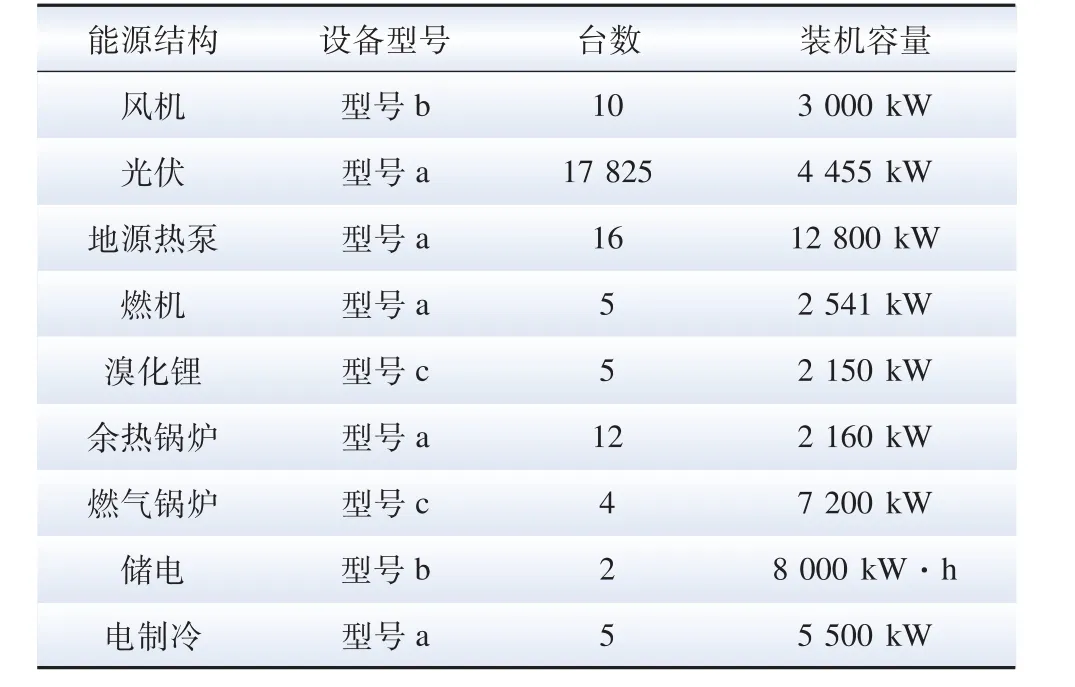
表2 場景1 規劃仿真結果Table 2 Planning simulation results of scenario 1

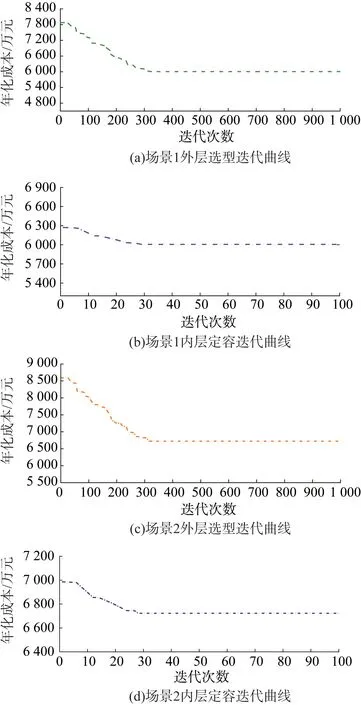
圖4 算法迭代曲線Fig.4 Iteration curve of scenarios

場景1 與場景2 的設備初始投資成本分別為18123 萬、15474 萬元。 僅從初始投資的角度上對比,場景2 要優于場景1。 但在場景2 下,其購電費用比場景1 高36.1%。

場景1 中各個月碳排放量差異性小,標準差為1745 kg,場景2 中各個月碳排放量差異性大,標準差為1933 kg。 主要是由于場景1 配置了熱電聯產設備,冬季產生的CO2量低于購買火電產生CO2的量。碳排放分析如圖5 所示,場景1 的碳排放量為47122 t,場景2 的碳排放量為49557 t。

圖5 場景1 與場景2 的碳排放量Fig.5 Carbon emissions of scenario 1 and 2

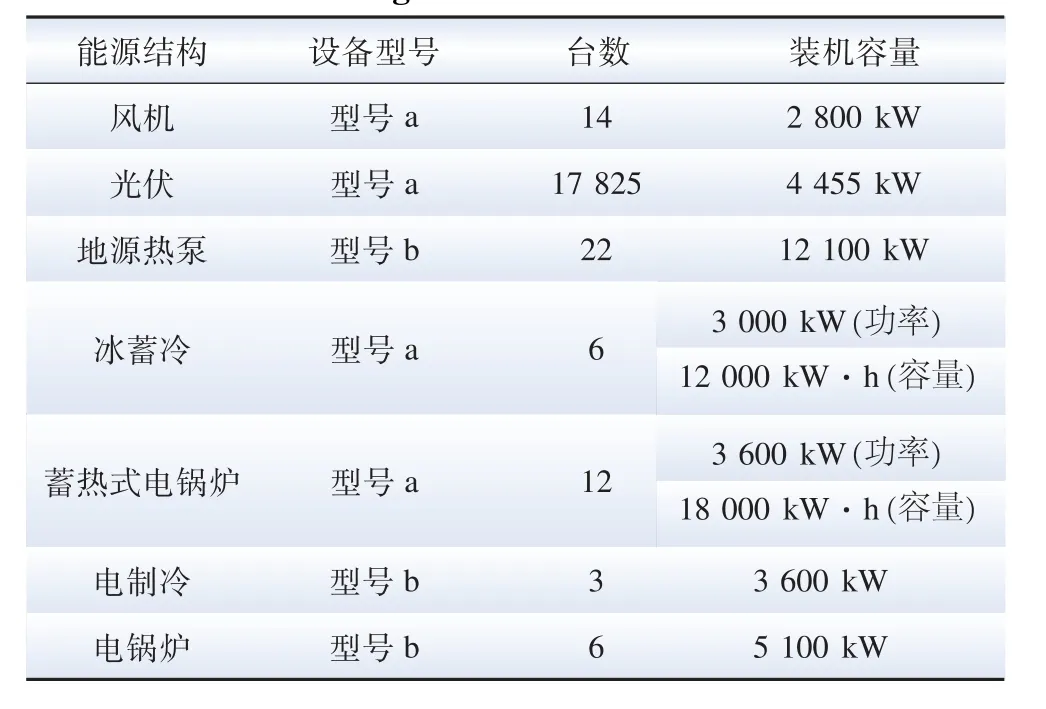
表3 場景2 規劃仿真結果Table 3 Planning simulation results of scenario 2

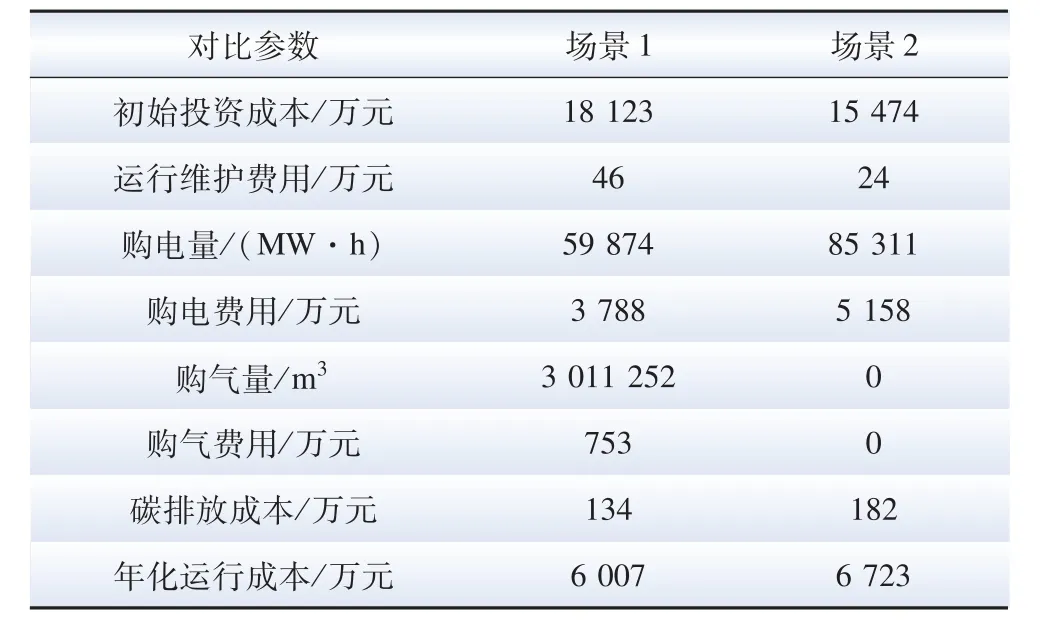
表4 規劃場景1 和2 經濟性對比Table 4 Economic comparison of planning scenario 1 and 2

4.2 典型日運行討論分析

夏季典型日中,2 個場景的能源購置成本曲線如圖6 所示。 場景1 與場景2 的購電成本分別為11.95萬、18.36 萬元。 場景1 為電-氣協調的供能系統,在本文的仿真條件下,場景1 能源消耗成本比場景2可降低約17.3%。

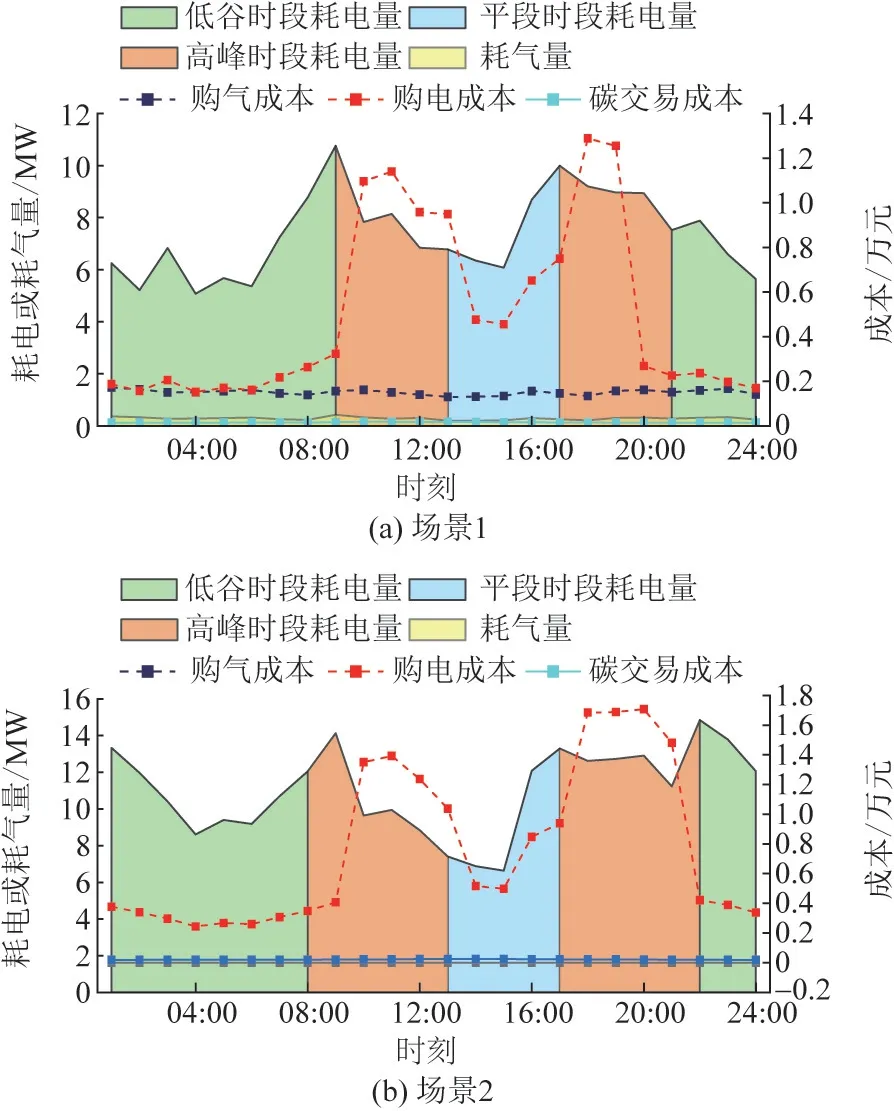
圖6 能源購置成本分析Fig.6 Analysis of energy purchase cost

通過對比2 種場景的規劃配置結果發現,場景1的投資成本高但是運行費用低,場景2 的投資成本低,但運行費用高。

4.3 選型分析

為對比不同設備型號對系統成本的影響,將場景1 中燃氣鍋爐型號由c 換為b,其余設備型號保持不變,以驗證設備型號選擇的有效性,將該場景定義為場景3。 場景3 的規劃仿真結果及其與場景1 的對比如表5、6 所示。

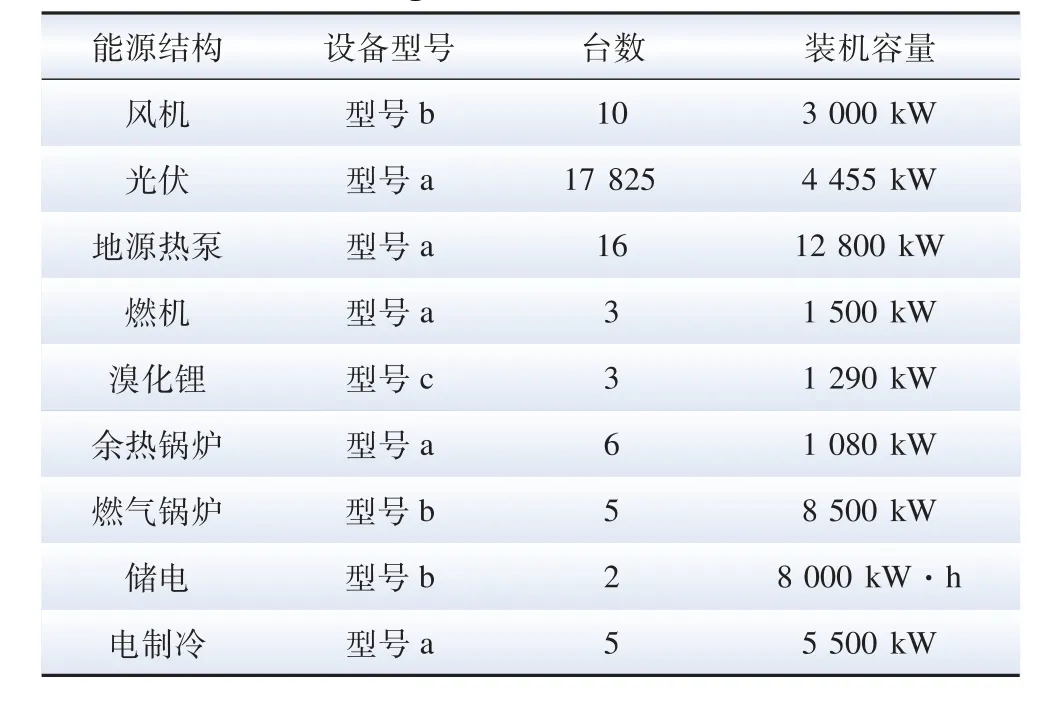
表5 場景3 規劃仿真結果Table 5 Planning simulation results of scenario 3

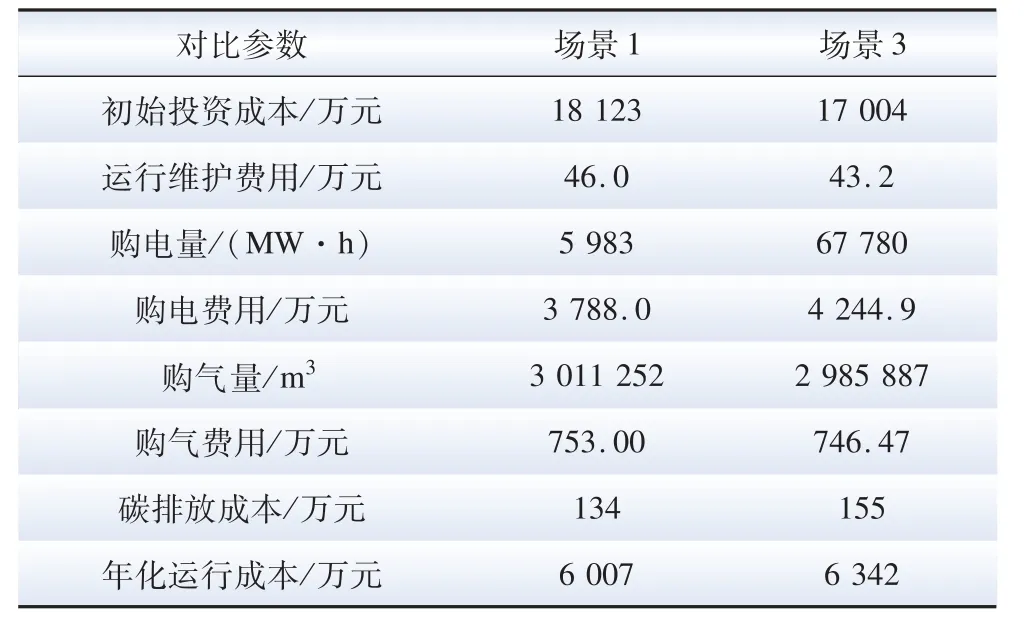
表6 規劃場景1 和3 的經濟性對比Table 6 Economic comparison of planning scenario 1 and 3

場景3 中,CCHP 系統和燃氣鍋爐的裝機容量比場景1 小,這導致在運行階段電制冷與地源熱泵的使用率增加,耗電量增加,運行成本變大。年化運行成本總體高于場景1,驗證了模型計算的有效性。

5 結論

本文提出的綜合能源系統規劃結構-型號-容量三級協調優化模型能夠解決以下問題:

1)解決綜合能源系統建設時規劃場景選擇問題,在實例庫數據量不斷豐富的基礎上,能夠提升實例推理計算結果與實際環境的匹配度。

2)解決設備型號組合優選及容量優化問題,可避免綜合能源系統建設選型時造成的容量冗余及設備效率低下的問題。

附錄A

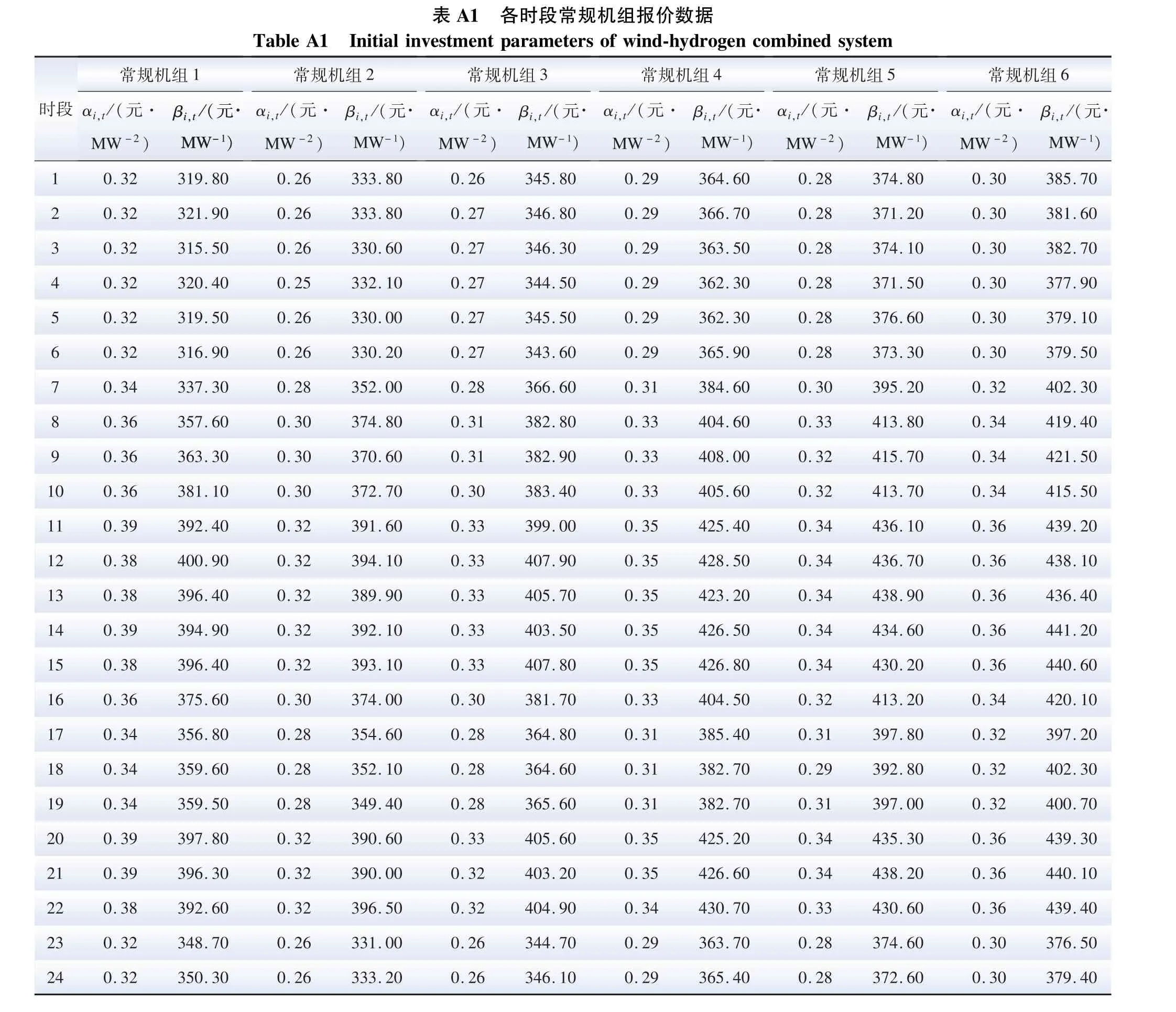
表A1 各時段常規機組報價數據Table A1 Initial investment parameters of wind-hydrogen combined system ?

表A2 風氫聯合系統初始投資參數Table A2 Quotation parameters of conventional units in each period ?

附錄A

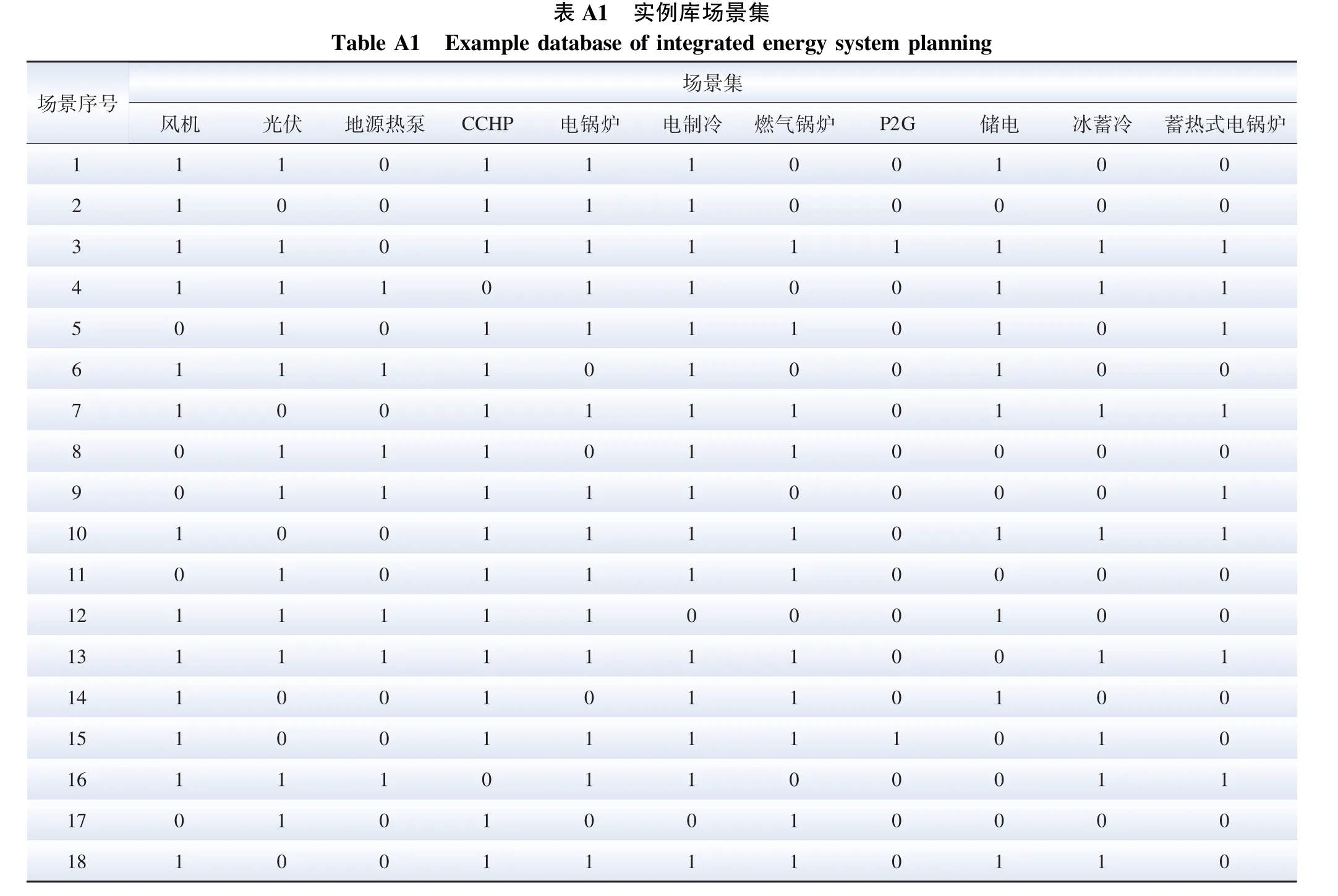
注:場景集合中0 代表未建設該設備,1 代表建設該設備。

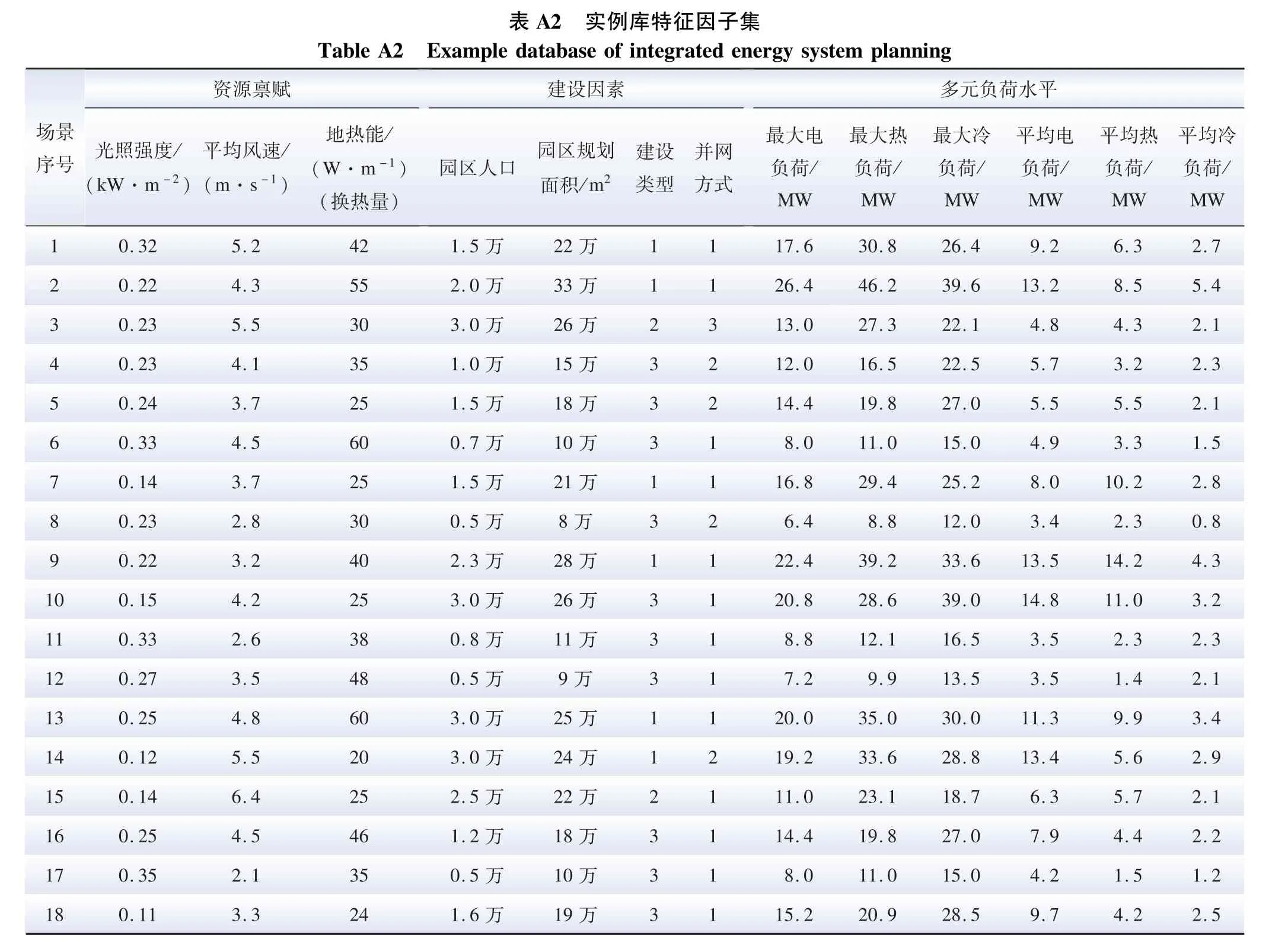
注:建設類型中,1 代表工業園區,2 代表海島園區,3 代表商業園區;并網方式中,1 代表并網上網,2 代表并網不上網,3 代表孤島型。

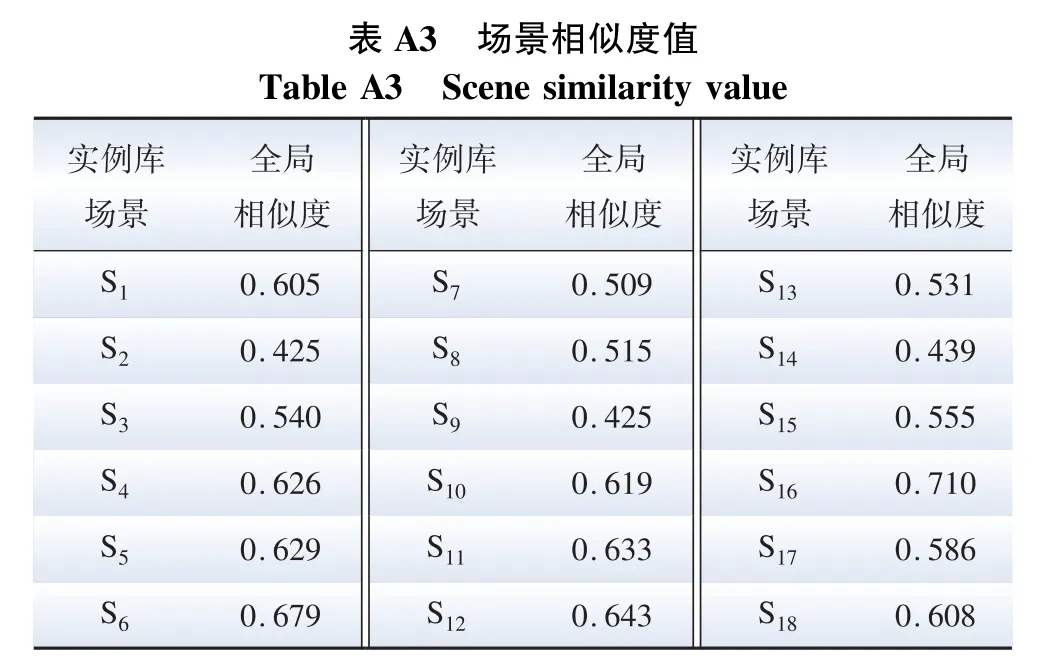
表A3 場景相似度值Table A3 Scene similarity value ?

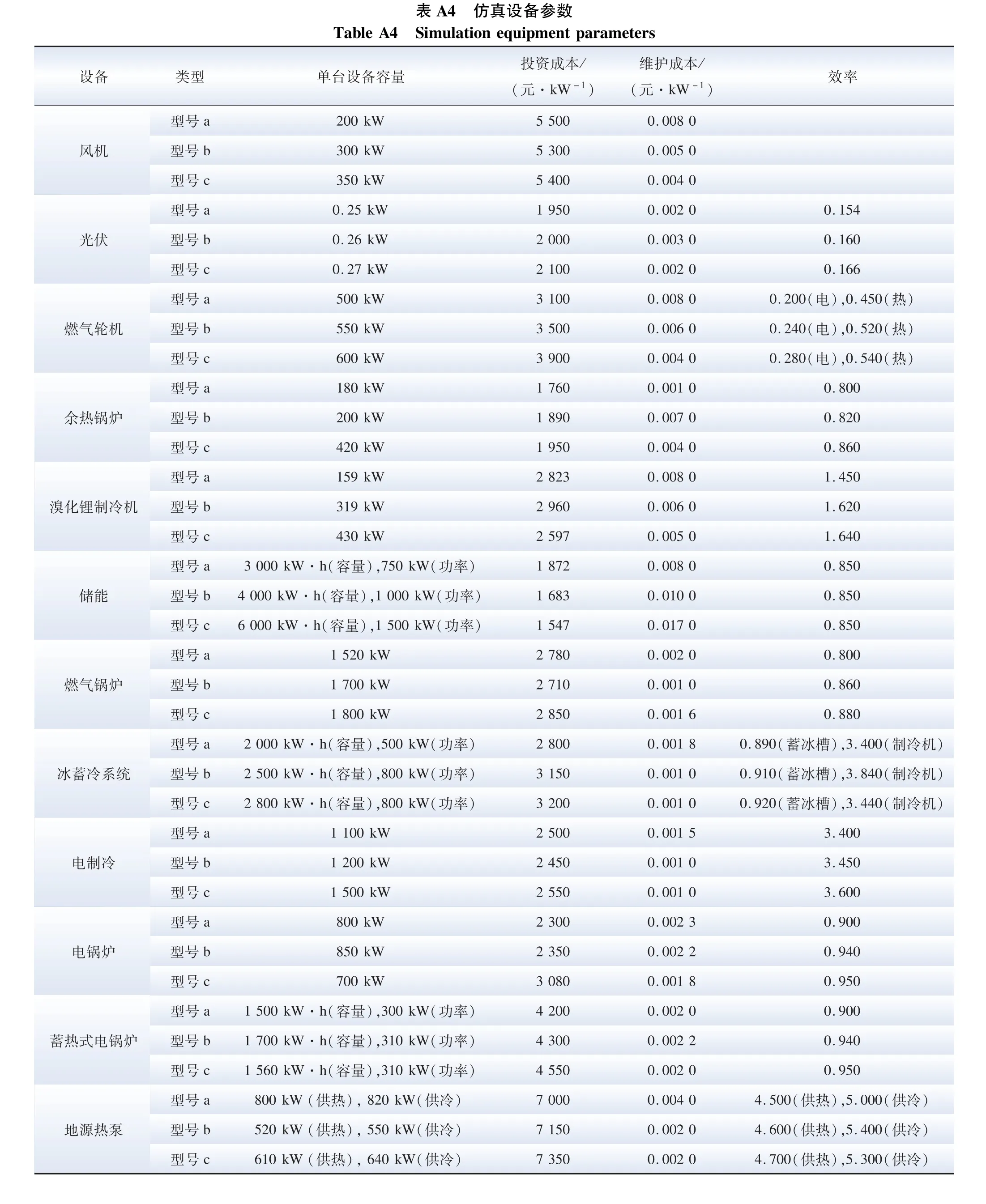
表A4 仿真設備參數Table A4 Simulation equipment parameters ?