一類截?cái)嗪瘮?shù)最優(yōu)化問題的求解方法

左鑫怡, 蔣 毅*, 楊 嵐

(1. 四川師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 四川 成都 610066; 2. 四川師范大學(xué) 可視化計(jì)算與虛擬現(xiàn)實(shí)四川省重點(diǎn)實(shí)驗(yàn)室, 四川 成都 610066)

1 預(yù)備知識(shí)

本文考慮一類截?cái)嗪瘮?shù)的最優(yōu)化問題

min{fi(x),hi(x)},

(1)

其中x∈Rn是變量,

f0:Rn→R∪{+∞},

fi,hi:Rn→R,i=1,2,…,m

min

截?cái)嗪瘮?shù)的最優(yōu)化問題(1)在稀疏性正則化[1-4]、基于穩(wěn)健估計(jì)的圖像恢復(fù)[5]以及穩(wěn)健回歸[6-9]等方面都有廣泛應(yīng)用.

關(guān)于這類截?cái)嗪瘮?shù)的最優(yōu)化問題(1),許多學(xué)者考慮hi(x)=α(α為常數(shù))的情況[1,10-11].Barratt等[10]首先利用截?cái)嗪瘮?shù)的相關(guān)公式得到問題(1)的等價(jià)模型,然后運(yùn)用啟發(fā)式方法的思想進(jìn)行求解.Liu等[11]提出了一種在低維空間下可得到全局最優(yōu)化的通用算法.Ong等[1]首先利用截?cái)嗪瘮?shù)的相關(guān)公式把問題(1)轉(zhuǎn)化為DC問題的形式,然后利用求解DC問題的算法對(duì)其進(jìn)行求解.本文考慮了hi(x)不是常數(shù)的情況,基于這些方法的啟發(fā),運(yùn)用了啟發(fā)式方法和ADMM方法的思想對(duì)問題(1)求解.

本文共分為三節(jié):第一節(jié)為預(yù)備知識(shí).第二節(jié)提出了截?cái)嗪瘮?shù)最優(yōu)化問題的兩種計(jì)算方法,第一種方法首先對(duì)問題(1)中的模型進(jìn)行等價(jià)替換,基于Barratt等[10]的研究,運(yùn)用啟發(fā)式方法的思想進(jìn)行求解;第二種方法是在截?cái)嗪瘮?shù)為非光滑函數(shù)的基礎(chǔ)上,運(yùn)用光滑逼近的思想使目標(biāo)函數(shù)光滑化,然后運(yùn)用ADMM方法[12]的思想進(jìn)行求解.兩種算法在滿足一定的條件下都可以得到全局最優(yōu)解.第三節(jié)應(yīng)用了本文提出的兩種計(jì)算方法求解經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化問題(ERM),給出數(shù)值實(shí)驗(yàn)結(jié)果,表明兩種方法都有效.

在本文中,所有向量都是列向量,In表示n×n單位矩陣.

2 計(jì)算方法

本節(jié)主要介紹求解截?cái)嗪瘮?shù)最優(yōu)化問題(1)的兩種計(jì)算方法:

第一種計(jì)算方法首先對(duì)問題(1)中的截?cái)嗪瘮?shù)進(jìn)行轉(zhuǎn)換,得到其等價(jià)模型,然后在文獻(xiàn)[10]的方法的啟發(fā)下,運(yùn)用啟發(fā)式方法的思想進(jìn)行求解.

第二種計(jì)算方法由于截?cái)嗪瘮?shù)是一個(gè)不可微函數(shù),因此應(yīng)用光滑逼近的思想使截?cái)嗪瘮?shù)光滑化,把問題(1)轉(zhuǎn)化為光滑的優(yōu)化問題,再運(yùn)用文獻(xiàn)[13-16]中ADMM算法的思想進(jìn)行求解.

下面介紹第一種計(jì)算方法.首先給出引理2.1,運(yùn)用該引理給出問題(1)的等價(jià)模型.

引理 2.1[8]函數(shù)min{fi(x),hi(x)}滿足

min{fi(x),hi(x)}=

由引理2.1,可推出截?cái)嗪瘮?shù)最優(yōu)化問題(1)等價(jià)于下列問題

0≤λi≤1,i=1,2,…,m,

(2)

其中λi∈R(i=1,2,…,m)和x∈Rn是變量.

對(duì)于問題(2),當(dāng)fi(x)可微時(shí),可以用非線性規(guī)劃方法求解,也可以用交替最小化求解.但在實(shí)際問題中發(fā)現(xiàn),對(duì)λi實(shí)行非精確交替最小化效果更好.

首先,固定問題(2)中的λi,求解相應(yīng)的最小化問題,將此時(shí)x的值記作xk.

然后對(duì)目標(biāo)函數(shù)關(guān)于λ計(jì)算其梯度

gi=(▽?duì)薒(xk,λ))i=fi(xk)-hi(xk).

λ的迭代如下

λk=Π[0,1]m(λk-1-βsign(g)),

其中sign是符號(hào)函數(shù),Π[0,1]m代表一種投影函數(shù),其解析式為

(Π[0,1]m(z))

下面給出算法2.1.

算法 2.1步驟 1 初始化:

λ0≥0,β>0,ε>0.

1) 計(jì)算xk+1:通過求解下列問題,使其取最小值時(shí)x的取值記為xk+1,滿足

gi=fi(xk+1)-hi(xk+1).

λk+1=Π[0,1]m(λk-βsign(g)).

算法2.1是一種下降算法,當(dāng)固定λi時(shí),問題(2)的目標(biāo)函數(shù)值在每次迭代后都會(huì)減少,并且因?yàn)棣薸的取值是有限的,所以這個(gè)算法可以保證在有限的時(shí)間內(nèi)終止.在實(shí)踐中,發(fā)現(xiàn)算法2.1在一定的條件下可以達(dá)到全局最優(yōu)解,而且在一些更復(fù)雜的情況下能實(shí)現(xiàn)得更好.

下面介紹第2種計(jì)算方法.

截?cái)嗪瘮?shù)最優(yōu)化問題(1)等價(jià)于下列問題

(3)

問題(1)中的截?cái)嗪瘮?shù)滿足等式

min{f1i(x),hi(x)}=

因此問題(1)等價(jià)于上述問題(3).由于絕對(duì)值函數(shù)是不可微的,所以本文利用絕對(duì)值函數(shù)

φ(x)=|x|

的光滑函數(shù)對(duì)其進(jìn)行逼近,應(yīng)用文獻(xiàn)[17-19]的如下光滑函數(shù):對(duì)任意p>0,

φ(x;p)=pln(ee

該光滑函數(shù)有如下性質(zhì).

引理 2.2[18]對(duì)任意p>0,光滑函數(shù)

φ(x;p):R→R+

滿足:

φ(fi(x)-hi(x);p):=

pln(ee

因此,關(guān)于原問題(1)的光滑無約束優(yōu)化問題定義為

(4)

引理 2.3問題(4)中定義的函數(shù)Φ(x;p)具有以下性質(zhì):

Φ(x;p1)<Φ(x;p2);

證明1)由引理2.2條件2),顯然成立.

Φ(x;p)-Φ(x)=

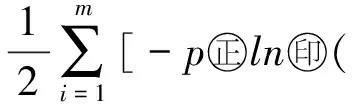
|fi(x)-hi(x)|]=

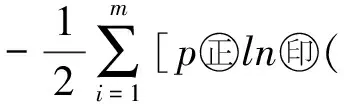
plne

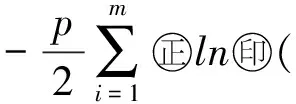
(5)

因此

0=ln1<
ln(ee
ln(1+1)=ln2.

(6)

由(5)式和(6)式可得

(7)

綜上所述,引理2.3得證.

由引理2.2和2.3可知問題(4)是問題(3)的光滑逼近.

(8)

考慮增廣拉格朗日乘子法[20],得

(9)

其中

Lβ(x,y,ω)=f0(x)+

下面介紹算法2.2.

算法 2.2步驟 1 初始化:

(y0,ω0)∈Rn×Rm,

p0>0,σ∈(0,1),

β>0,ε1>0,ε2>0.

xk+1:=argxminLβ(x,yk,ωk);

yk+1:=argyminLβ(xk+1,y,ωk);

ωk+1:=ωk+β(xk+1-yk+1);

4) 若

‖xk+1-yk+1‖<ε1

且

‖-β(yk-yk+1‖<ε1,

pt+1=σpt,

算法2.2是對(duì)變量進(jìn)行交替最小化,若問題(7)中的目標(biāo)函數(shù)滿足文獻(xiàn)[9]中的相關(guān)條件可得到全局最優(yōu)解.

3 舉例說明

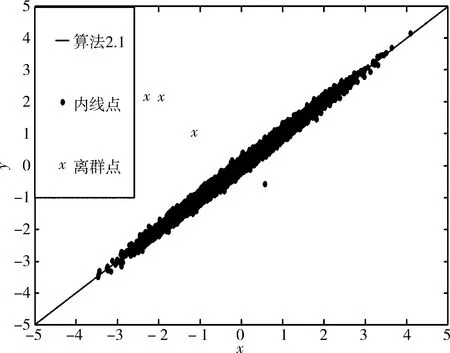
在本節(jié)中,使用AMDR5 2.1GHz個(gè)人電腦,在MatlabR2019b環(huán)境下,應(yīng)用算法2.1和算法2.2分別求解如下經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化(ERM)問題

其中x1,…,xN∈Rn,y1,…,yN∈Y,Y是輸出空間,θ∈R是擬合參數(shù),l:R×Y→R是損失函數(shù),r:Rn→R是正則化函數(shù).

這里把l(xTiθ,yi)≥0.5的點(diǎn)(xi,yi)視為離群點(diǎn),其余的視為內(nèi)線點(diǎn).在一些實(shí)際問題中ERM問題執(zhí)行得很好,但是當(dāng)數(shù)據(jù)中具有離群點(diǎn)時(shí),它的性能就很會(huì)很差,因此本文考慮下列截?cái)嗷貧w模型

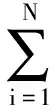
(10)

下面對(duì)具有離群點(diǎn)的數(shù)據(jù)進(jìn)行擬合.

然后隨機(jī)選取5個(gè)點(diǎn),將這5個(gè)點(diǎn)中的yi轉(zhuǎn)化為-yi，

xi～N(0,1),yi=xi+0.1zi,
zi～N(0,1),i=1,2,…,N.

最后應(yīng)用算法2.1和算法2.2求解截?cái)嗷貧w模型(10).

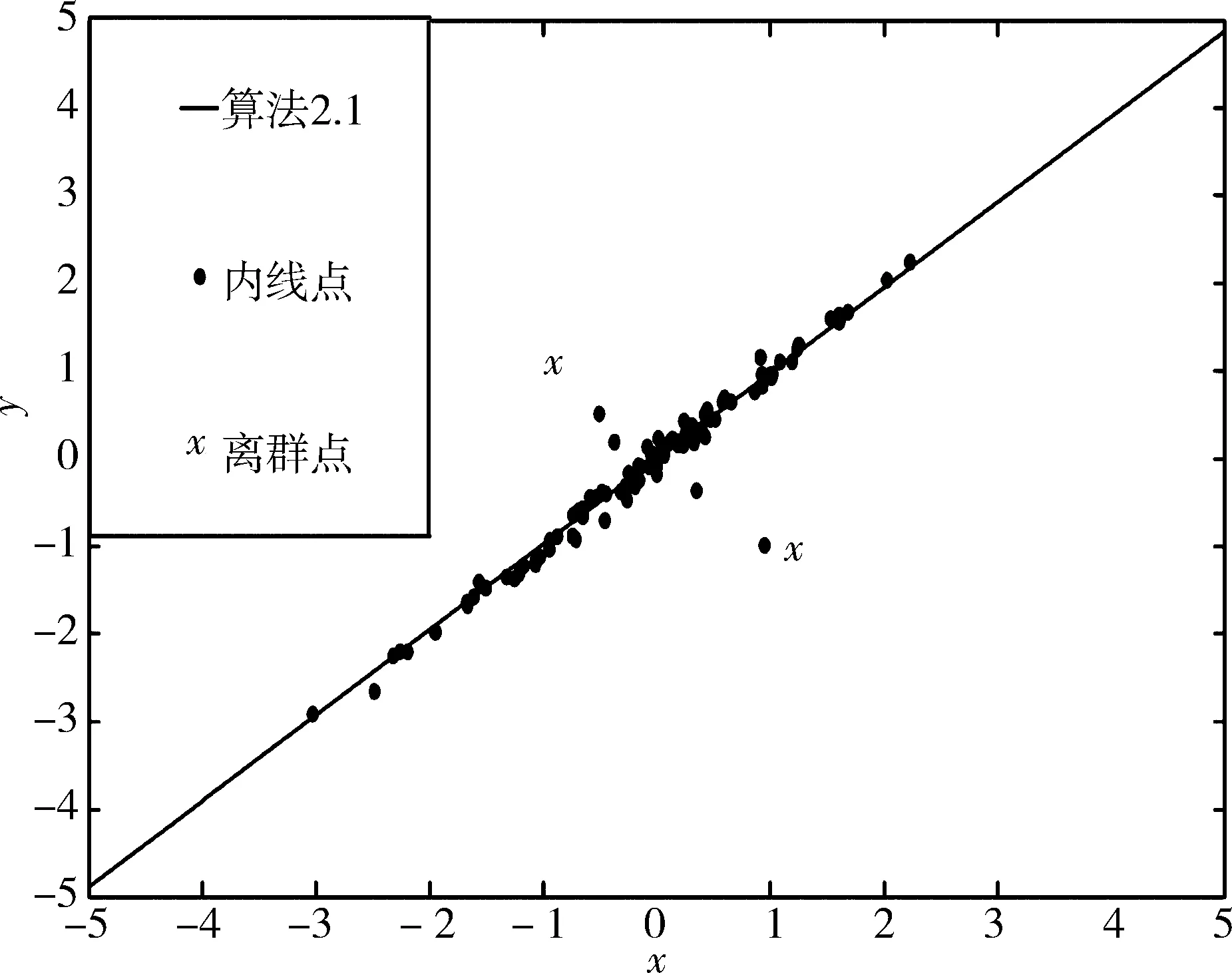
(a) N=100時(shí),算法2.1的計(jì)算結(jié)果

數(shù)值實(shí)驗(yàn)結(jié)果表明兩種計(jì)算方法都有效,并且算法2.1的速度更快.