水下纜索運動建模與仿真分析方法

張 斌，劉延平

（1. 中國船舶集團有限公司第七一〇研究所，湖北 宜昌 443003；2. 清江創新中心，湖北 武漢 430076）

0 引言

隨著對海洋開發利用的不斷深入，各類水下無人錨泊駐留系統、海洋拖曳系統逐漸成為相關熱點研究領域，準確預報分析錨泊、拖曳等系統在海流等外界環境擾動下的動態運動響應成為其工程設計的關鍵。其中，建立用于連接設備、傳遞或緩沖載荷、傳輸能源和信號等用途的柔性纜索的運動學與動力學精確建模是一項難點技術。

水下柔性纜索的力學、運動學特征與錨泊、拖曳系統整體狀態耦合相關，并交互影響，且隨著外部載荷變化呈現非線性時變狀態，難以對描述其狀態的微分方程進行直接求解，通常在滿足動力學條件和連續性條件下，采用有限差分[1-2]、集中質量[3-4]、有限段[5-6]等空間域內的物理離散方法對連續纜索控制方程進行近似求解。

在水下纜索中內部張力占主導作用情況下，可忽略纜索單元空間旋轉運動，上述線性離散化求解方法可取得較好的計算精度和準確性。但在處理多點懸鏈系留、錨泊狀態振蕩急劇變化、拖船大范圍轉向等易于出現纜索低張力松弛、非線性大形變等問題時，線性離散單元無法準確反映描述纜索空間曲率引起的彎矩、扭矩作用，難以描述纜索真實空間狀態與內力狀態，進而出現數值求解奇異。通過選取大量離散節點進行更加細的線性單元劃分來逐漸逼近纜索真實輪廓，不僅算力消耗劇增，也面臨數值積分截斷誤差與舍入誤差累加問題導致的計算錯誤。

因此，本文改進柔性纜索的線性離散化單元為高階非線性單元，采用三次樣條插值描述纜索微元的空間形態，通過加權余量法解決插值方法僅能在離散節點位置滿足纜索狀態微分方程問題，消除微元長度范圍內殘差，提供一種高效、準確求解水下纜索復雜運動狀態的新方法。

1 水下纜索空間運動數學模型

引入圖1中所示的慣性坐標系O（xe，ye，ze）、纜索局部坐標系 S（q1，q2，q3）以及弗萊納坐標系 S（t，n，b）。

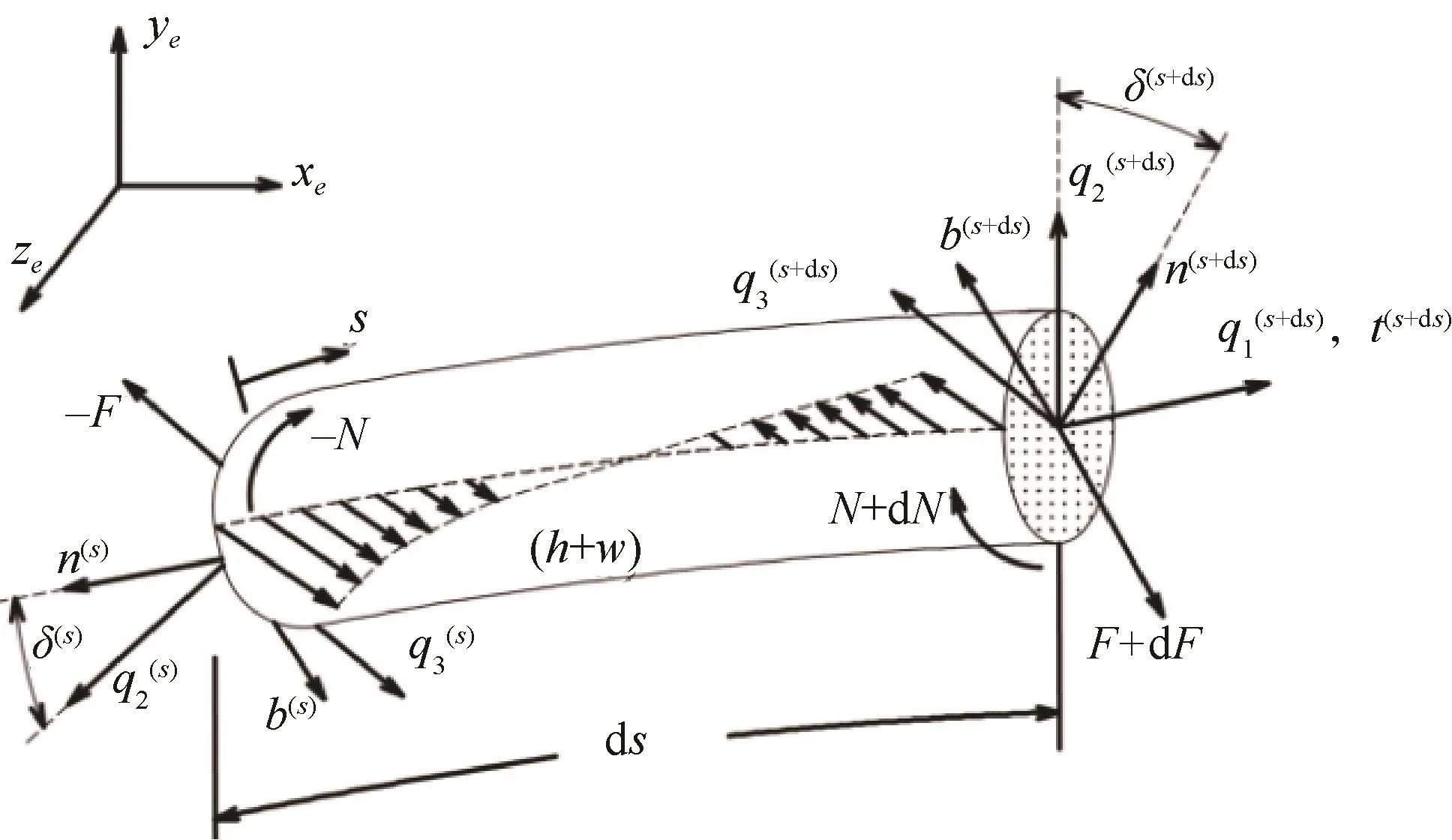
圖1 坐標系選取及水下纜索微元力學狀態Fig.1 Coordinate systems involved and micro-elements force of the cable element

對于長度為ds的纜索微元，其在流體作用力、自身體積力、內部張力等共同作用下，大地坐標系中空間平移與旋轉運動的微分控制方程如下[7]：

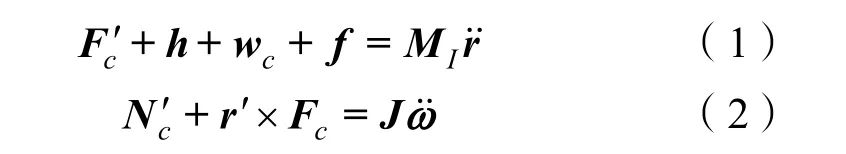
式中：Fc為微元內部張力矢量；h為微元長度上的流體作用力；wc為微元水下濕重矢量；f為其他外部作用力；MI為纜索微元質量矩陣；r（s，t）為纜索微元的空間構型曲線矢量；Nc為微元內部的彎矩、扭矩矢量；ω為纜索微元的旋轉角速度矢量陣。

應綜合考慮坐標系S（q1，q2，q3）以及S（t，n，b）本身不重合導致的角間距 δ（s，t）偏差，與纜索微元形狀扭轉變形共同組成總撓率[8]：

纜索微元內部任一點處力矩矢量可表述為沿弗萊納坐標系 b軸方向的彎矩以及沿 t軸方向的扭矩[9]：

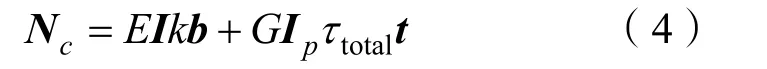
式中：I為纜索橫截面慣性矩；Ip為纜索橫截面極慣性矩；G為纜索的材料剪切模量。

水下纜索大長細特性使得其轉動慣量矩陣 J本身較小，且其法向阻力系數一般以量級差距遠大于切向阻力系數，進一步限制其產生旋轉角加速度，大地坐標系中其旋轉控制方程等式右半部分為2個極小值乘積，可認為水下纜索微元內部力與力矩形成近似平衡狀態，可得：

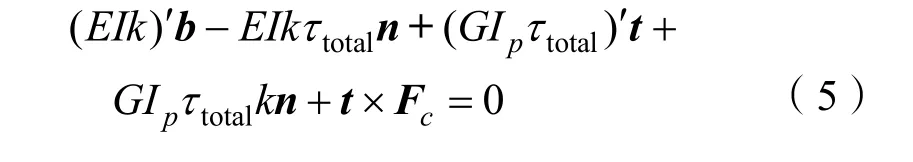
與弗萊納坐標系單位矢量t叉乘，去除上述旋轉運動控制方程中沿切向t并對內部力矩無影響分量部分，可得：

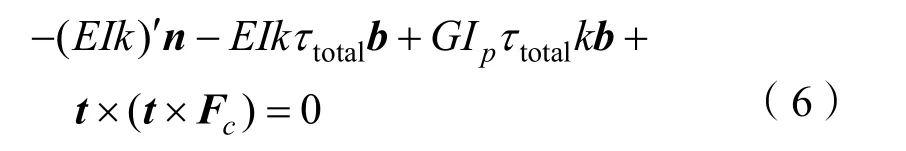
通過叉乘反交換率與拉格朗日公式計算上式中連續叉乘，可得到沿水下纜索微元軸向任意位置處的內部張力矢量：

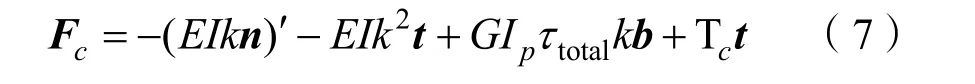
式中，TC為纜索內部軸向拉力。

通過水下纜索微元空間構型曲線r(s, t)描述弗萊納坐標系各軸線矢量方向，具體形式如下：

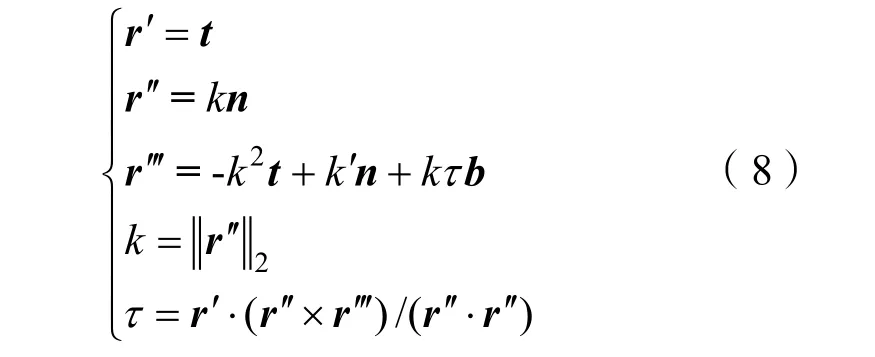
可將內部力 FC從弗萊納坐標系中轉換至大地坐標系中，簡化對于彎曲、扭轉等力矩作用效果的求解。

水下纜索微元大地坐標系中空間平移運動方程可寫為如下形式，包含了微元中軸向拉力、扭轉應力、彎曲應力對于纜索空間形態r(s, t)的影響：

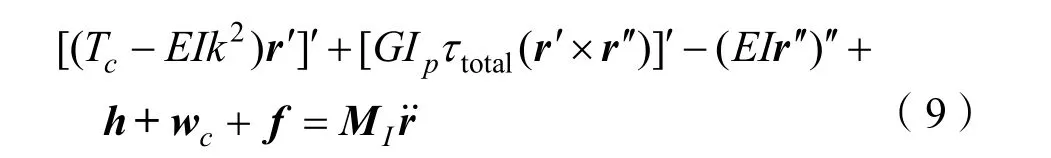
由于水下纜索中扭矩沿軸向連續且恒定，可知旋轉運動控制方程在弗萊納坐標系t軸方向投影必定為0：

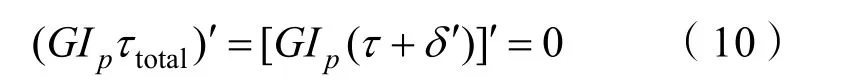
上式給出了坐標系S（q1，q2，q3）以及S（t，n，b）本身不重合導致的角間距 δ（s，t）偏差的計算方法，進而可以確定坐標系 S（q1，q2，q3）的坐標軸指向。

2 水下纜索運動控制方程離散化求解

2.1 水下纜索非線性離散化單元構造

由連續纜索運動控制方程計算推導過程可知，坐標系矢量軸方向、纜索形變量均可通過纜索空間形態r（s，t）及角間距δ（s，t）求解得到。

在空間域內對水下纜索進行離散化處理，將其劃分為N段長度為ds的非線性高階單元。根據[A1]大地坐標系下節點坐標值 r（i）（i=1，2…N，N+1）通過3次樣條差值方法構造試函數逼近空間樣條曲線的真實分布狀態，二階連續可導既滿足空間曲率連續要求，又能避免更高階函數帶來的額外方程求解問題。

圖2 水下纜索非線性單元劃分Fig.2 Non-linear element of the underwater cable

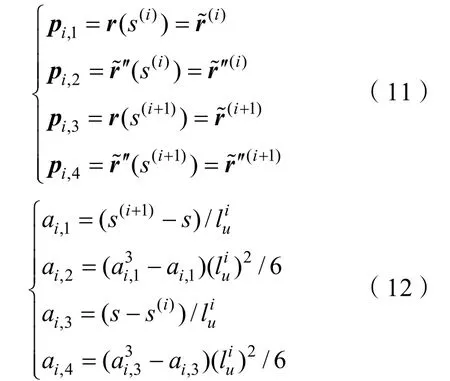
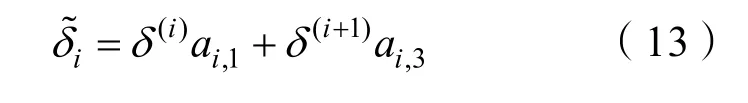
2.2 加權余量法求解

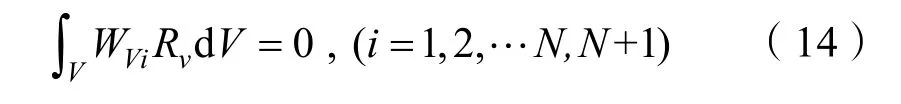
式中：Wvi是求解域內的權函數；Rv為試函數偏差產生的計算殘數；V為去除邊界后的求解計算域。

選用Galerkin方法為求解具體方法，其權函數與基函數一致，可將微分方程轉換為一系列對稱的代數方程，實現計算收斂的同時進一步減小算力需求。對于第i（i=1，2…N，N+1）段非線性纜索微元，其計算域內的余量消除方程為

受篇幅所限，纜索單元求解域內部張力、流體力、體積力、彎曲力、扭轉力等矩陣的具體形式不再贅述[11-12]。

方程（17）-（18）完整描述了每一段纜索單元空間平移與旋轉運動。對于纜索節點i，其廣義運動速度和加速度在其前后兩段纜索單元運動控制方程中體現，將第i-1段、第i段單元中關于節點i的相關項疊加整合，可得節點1至節點N處運動方程：

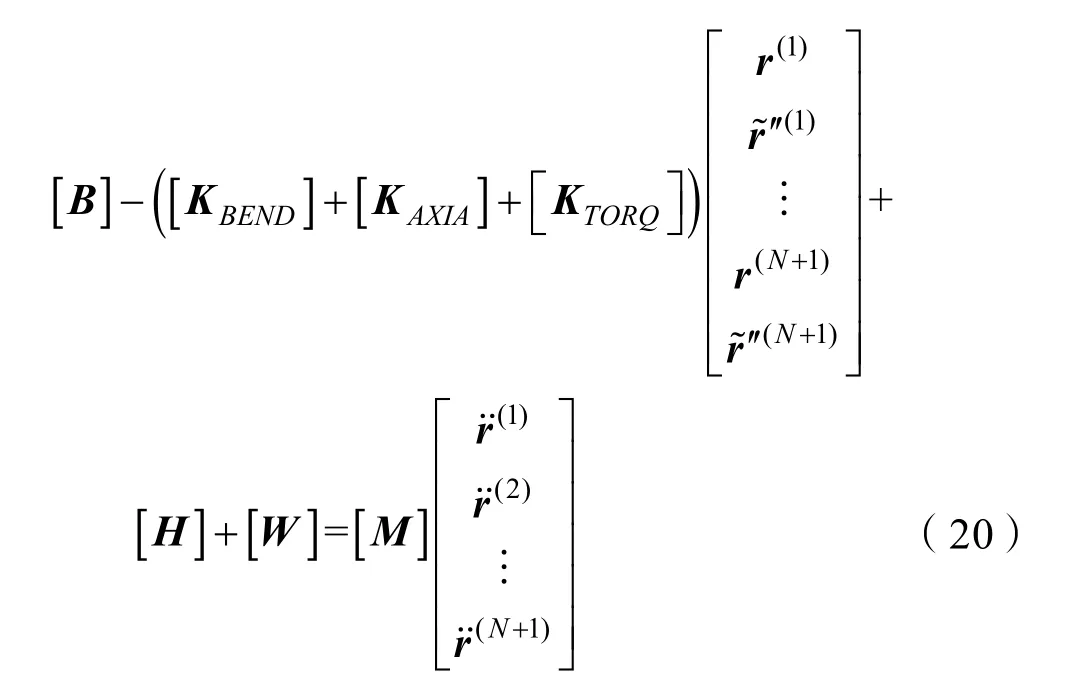
式中：[H]、[W]、[B]為各離散節點疊加整合后的流體作用力、纜索質量及浮力矩陣；[M]為（3N+3）階質量矩陣；[KAXIA]、[KBEND]、[KTORQ]為各離散節點疊加整合后的軸向張力、彎曲作用力、扭轉作用力矩陣，為（3N+3）×（6N+6）階形式矩陣。

對于常見的水下錨泊系統、拖曳系統，纜索上一般無外部額外施加力矩，因此，可將非線性纜索單元的扭轉運動約束方程整合為如下形式，計算中需指定水下纜索首節點扭轉形變角δ（1）或末節點處扭轉形變角 δ（N+1）以固定一個扭轉自由度，使得該約束方程左側系數矩陣變為滿秩矩陣，進而獲得唯一解。

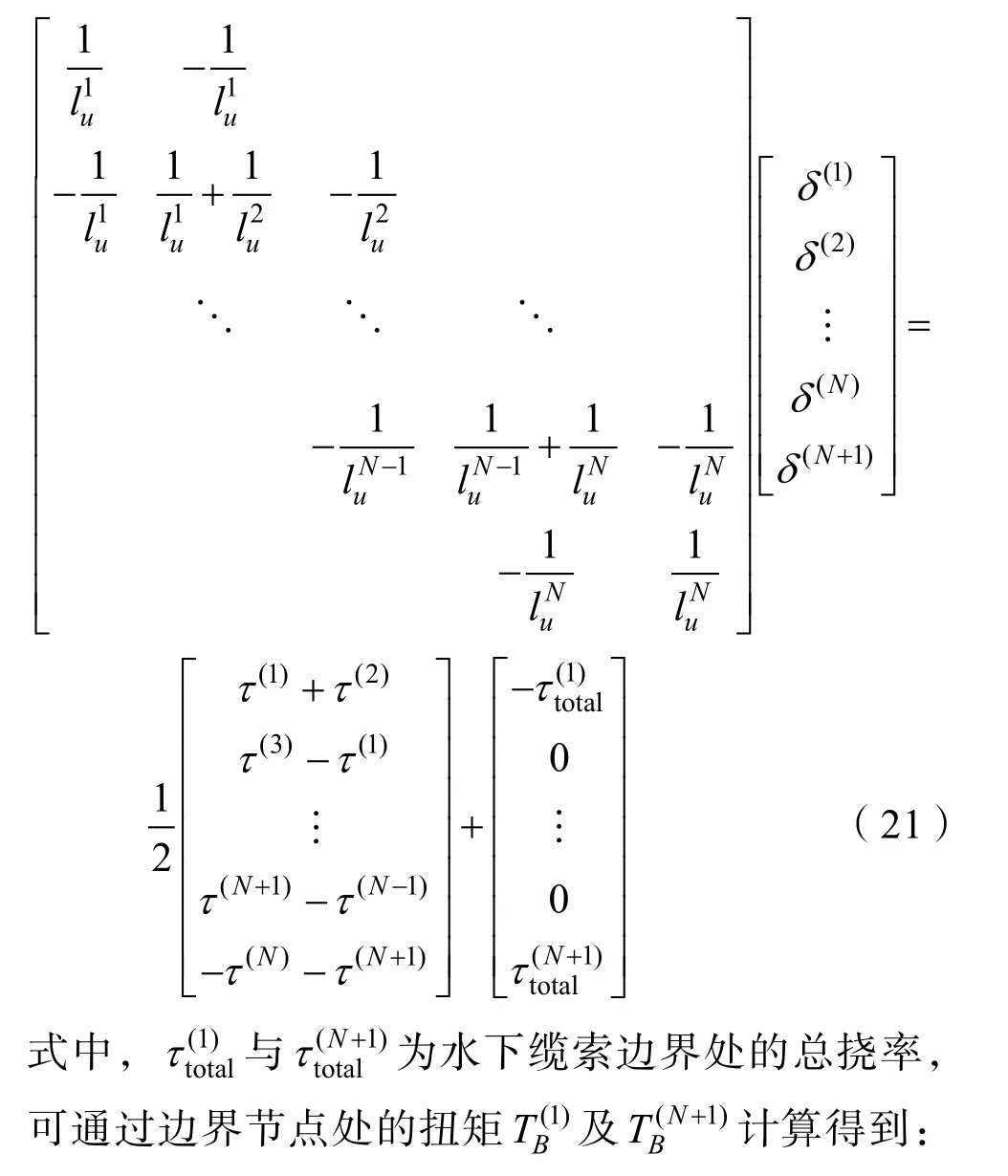
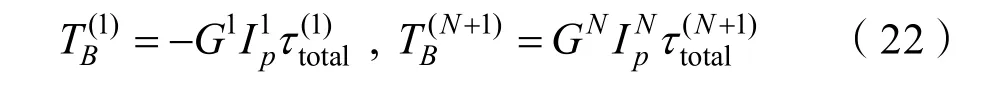
3 模型驗證

3.1 Hopland拖曳試驗驗證

采用1992年Hopland進行的通信光纜拖曳布放實海實驗測試數據作為對比算例[13]，通過水下纜索運動模型對其重型鎧裝拖纜在拖船加減速過程中動態變化情況。

該纜索主要物理特性如下：直徑33.2 mm，總長 300 m，密度 3 121 kg/m3，彈性模量77.5×109Pa，抗彎剛度1 000 N·m2，法向阻力系數1.649，切向阻力系數0.12。

加速實驗過程中，拖船以約1.1 kn勻航速拖動纜索達到穩定狀態，隨后進入加速拖曳階段，拖船速度在60 s時間內均勻增大至2.4 kn。計算模型仿真計算結果如圖3所示，圖中，t=0時刻的纜形圖對應于1.1 kn均勻航速拖曳下纜索狀態，t=60 s時刻，拖船線性加速達到2.4 kn，由仿真結果可知，拖纜其重新趨于穩態時間滯后約360 s。

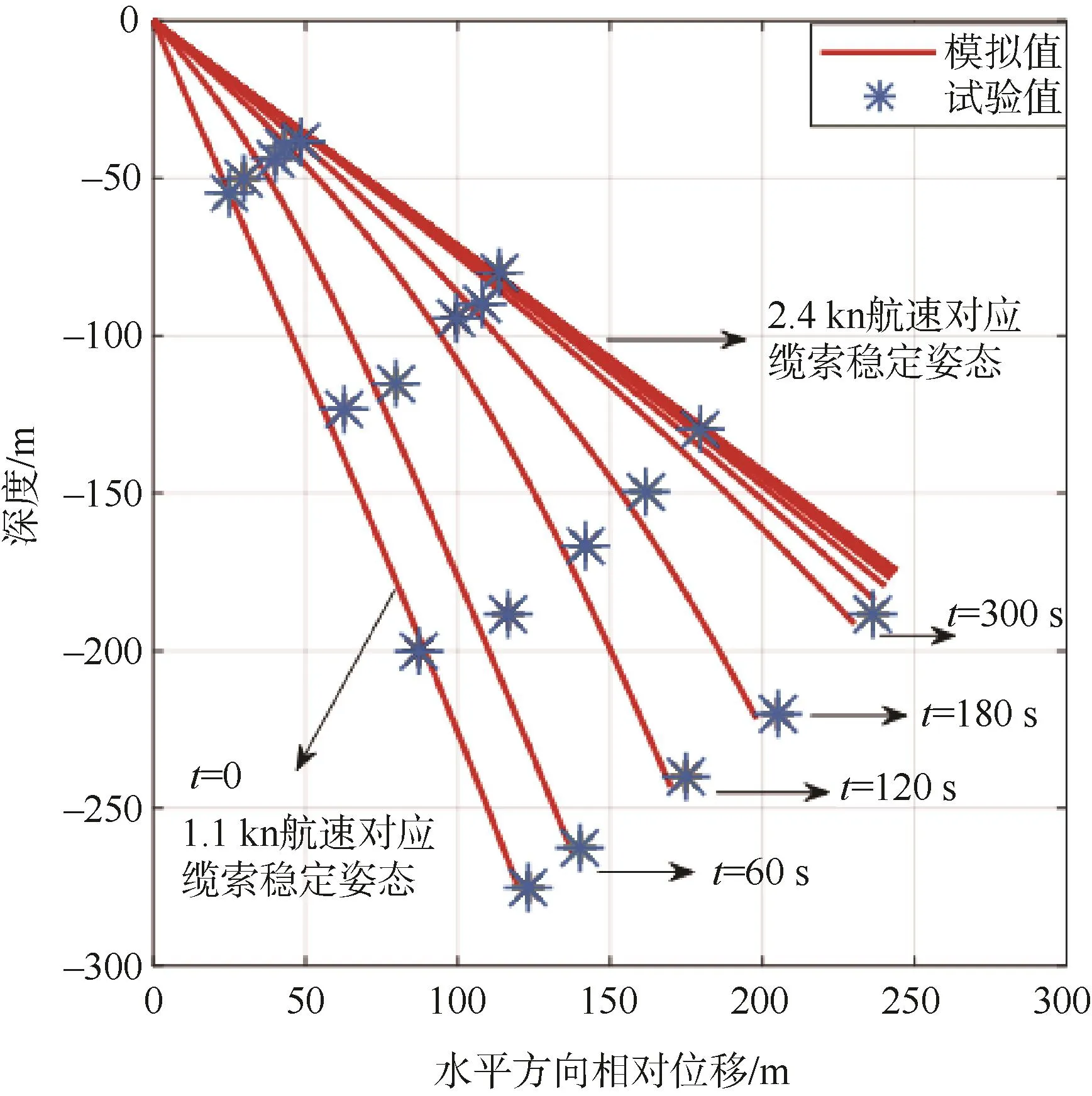
圖3 拖船加速過程HA纜姿態變化Fig.3 Attitude change of HA cable during the towing ship accelerating process

減速實驗過程中，拖船以約2.5 kn勻航速拖動纜索達到穩定狀態，隨后進入減速拖曳階段，拖船速度在60 s時間內均勻降低至1.0 kn。計算模型仿真計算結果如圖4所示，圖中t=0時刻的纜形圖對應于2.5 kn均勻航速拖曳下纜索狀態，t=60 s時刻，拖船線性減速達到1.0 kn，由仿真結果可知，拖纜重新趨于穩態時間滯后約460 s。

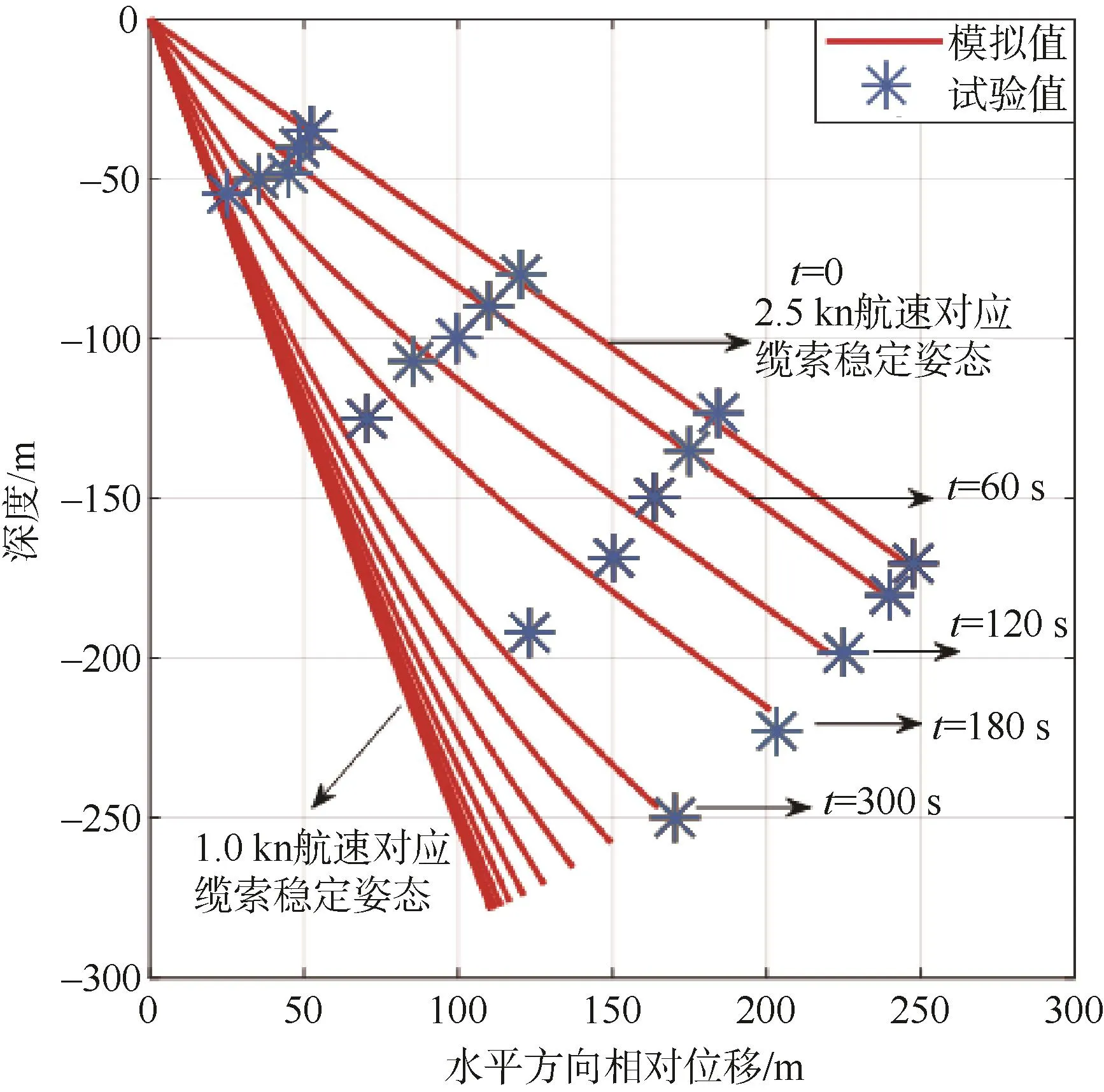
圖4 拖船減速過程HA纜姿態變化Fig.4 Attitude change of HA cable during the towing ship decelerating process

綜合上述實驗測試纜索形態變化及 Hopland實測的纜索節點空間位置坐標，可以看到數值模擬數據與實驗數據吻合度及變化規律高度一致，僅存在細微偏差，推測是由于實驗測量誤差及實驗過程中海流流速影響等導致。

3.2 細長柔性桿件彎曲形變計算驗證

通過與可精確求得解析值的經典細長柔性桿件受力彎曲形變模型進行比對分析，驗證本計算模型中高階非線性微元劃分及加權余量方法消除殘差趨近物理模型真實空間形態方法的準確性，也直接對模型中彎曲應力的影響結果進行比對分析。

本算例的物理模型為一端固定約束、一段自由的細長柔性桿件，對其末端施加豎直向下集中載荷P。由材料力學相關解析求解方法可知，細長桿上任一點處曲率半徑如下：

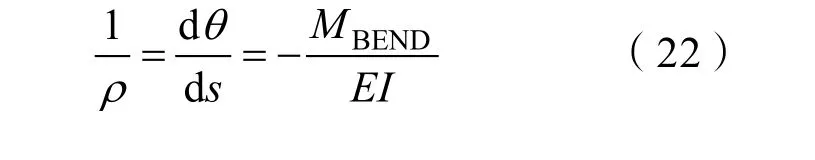
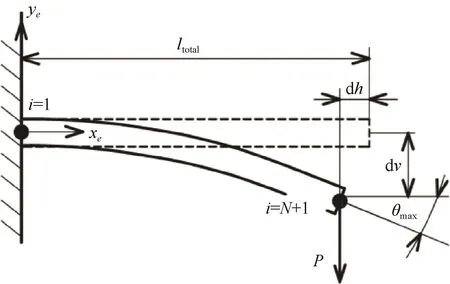
圖5 細長柔性桿件彎曲形變計算驗證模型Fig.5 Bending deformation validation model of flexible rod

式中：MBEND為該點位置彎矩；E為材料彈性模量；I為桿件的橫截面慣性矩；θ為該點彎曲形變后繞中心軸轉動角度；s為撓度曲線弧長。

上述末端節點的位移量、偏轉角可通過數值積分求解方法獲得準確值。

本算例模型相關計算參數如下：直徑20 mm、長度10 m、密度1 000 kg/m3、彈性模量2×1011Pa。采用高階非線性離散化模型建立桿件的運動控制方程，仿真分析不同集中力載荷P施加狀態下桿件形態及末端節點坐標值，具體結果如圖6所示。

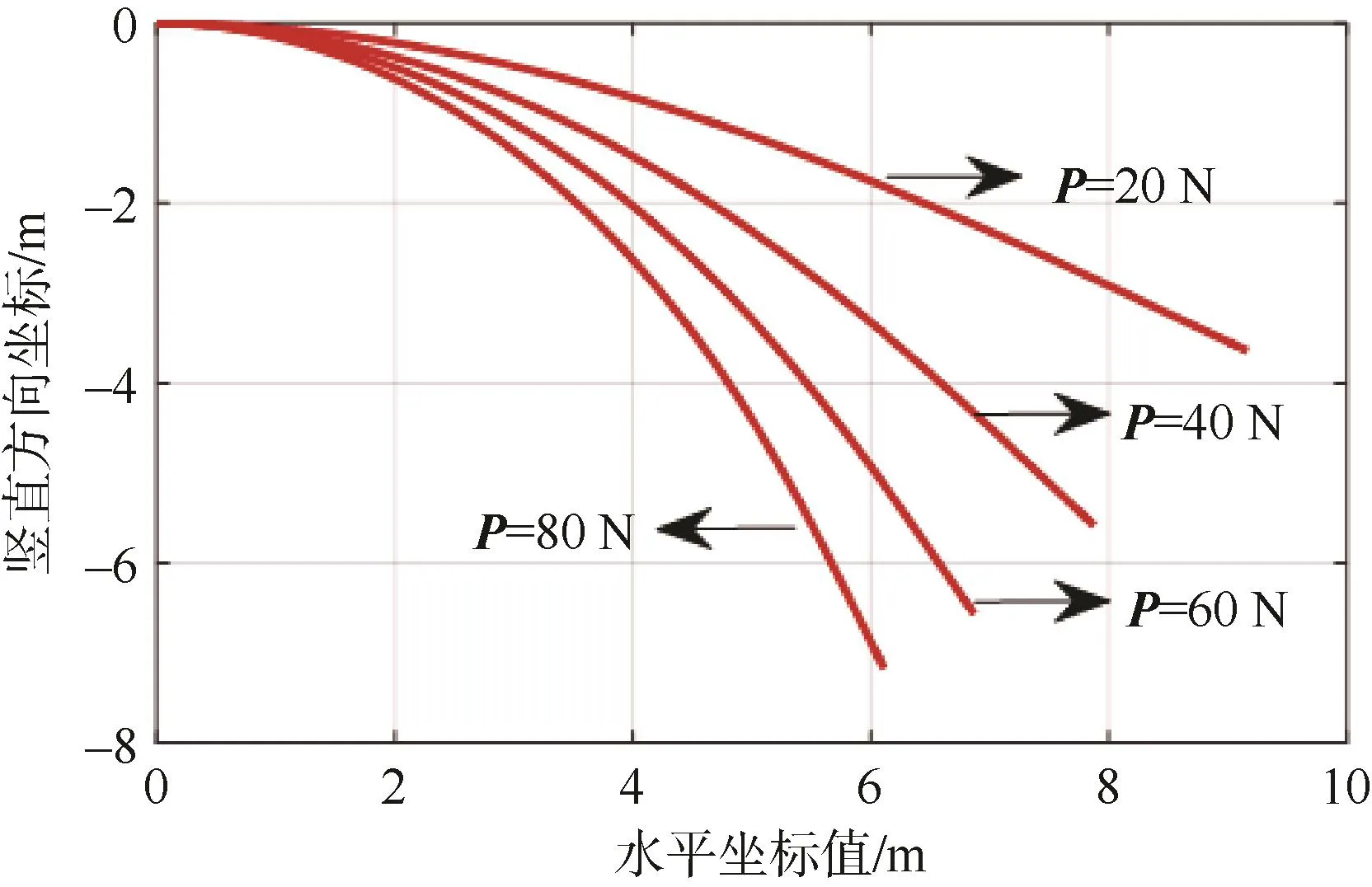
圖6 不同集中載荷作用下細長桿平衡姿態Fig.6 Torque equilibrium attitude of the flexible rod with different loading

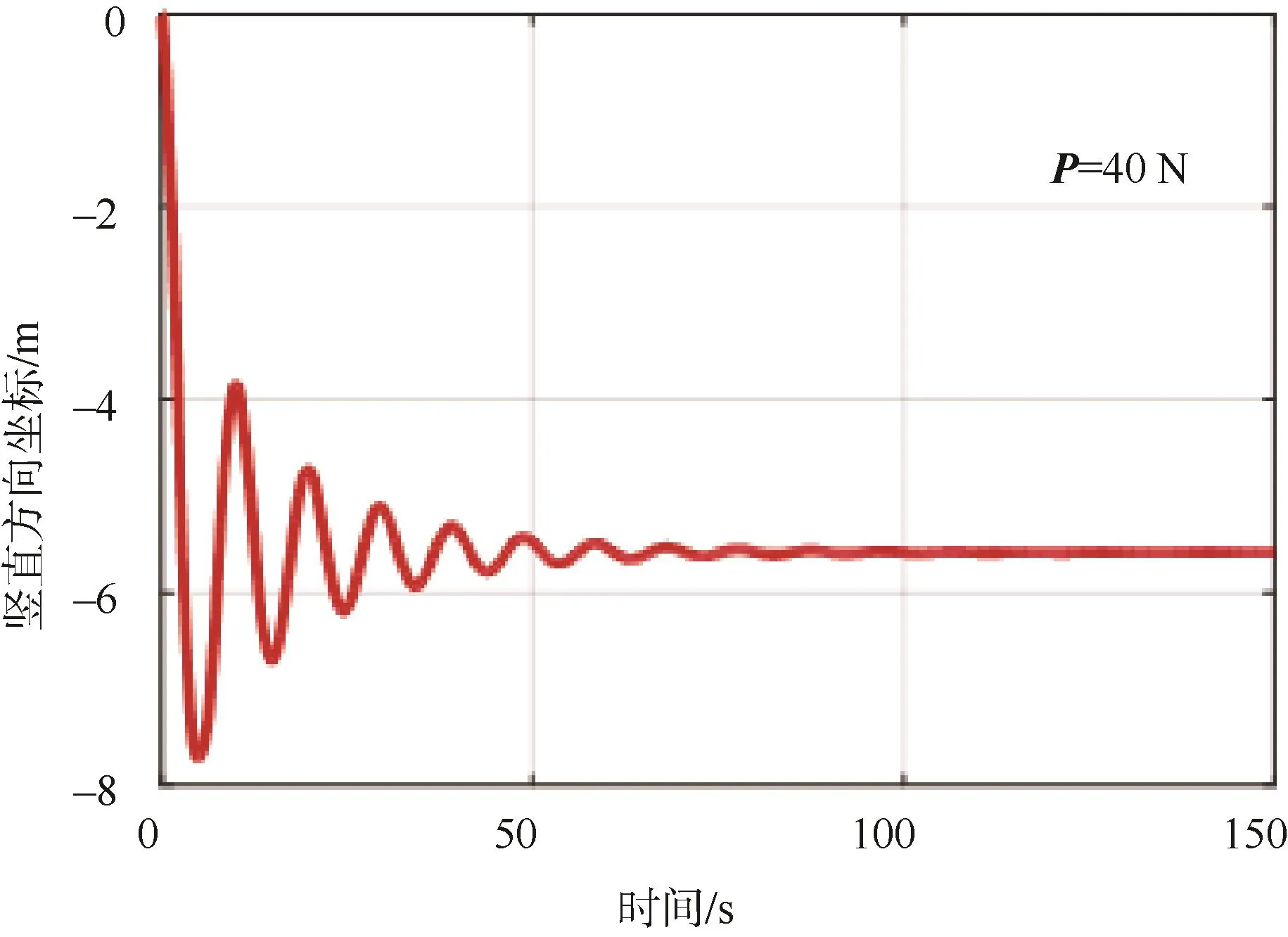
圖7 末端節點坐標值隨時間變化情況Fig.7 Change of the end node’s coordinate value with time

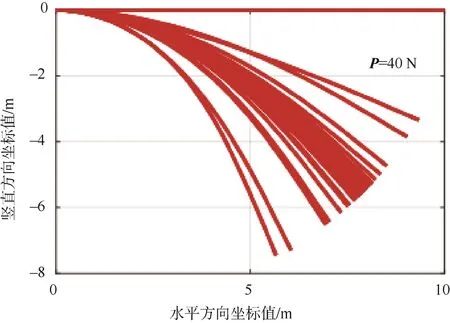
圖8 桿件形態隨時間變化情況（Δt=2 s）Fig.8 Change of the attitude of the flexible rod with time（Δt=2 s）

由計算結果可知，桿件末端節點在集中載荷P的作用下逐漸偏轉，在彎曲應力與載荷P共同作用下，節點在平衡位置附近做欠阻尼振蕩并逐漸趨于穩定狀態。

不同計算約束條件下，使用本文建立的運動控制模型求解得到的末端節點坐標值與解析值結果相對誤差ε如下表所示，具體計算方法為

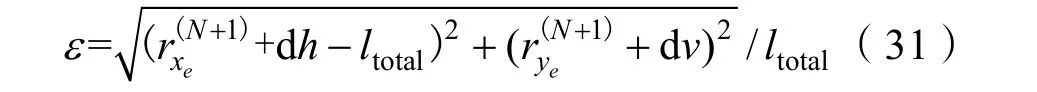
由計算結果可知，通過高階非線性微元物理離散方法建立的運動控制方程具有較高計算精度。

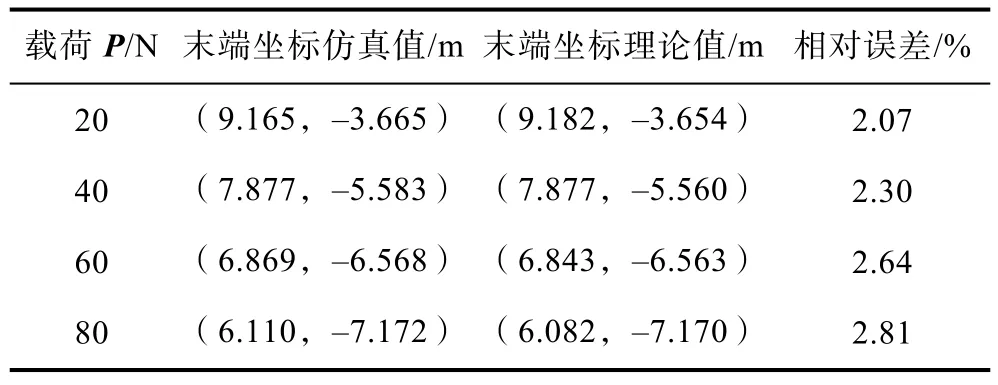
表1 細長柔性桿件彎曲形變計算結果比對Table 1 Comparison of the simulation value and theoretical value of the flexible rod

4 結束語

本文將水下纜索線性化離散改進為高階非線性單元，建立了包含彎矩、扭矩作用的水下纜索狀態微分方程數值求解模型，通過與Hopland水下纜索拖曳試驗數據、細長柔性桿件彎曲形變計算等對比分析，驗證了本文高階離散求解模型的準確性，可為水下錨泊系留、水下拖曳等系統復雜運動狀態高效求解與工程設計提供有價值的參考。